Хелпикс

Главная

Контакты

Случайная статья



Свойства криволинейного интеграла



Свойства криволинейного интеграла

1) Значение криволинейного интеграла (величина работы A) зависит от подынтегрального выражения, от формы кривой интегрирования и от направления движения по линии L, т.е. по дуге PQ. Если на дуге PQ изменить направление движения на противоположное, то вектор 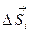 изменит направление на 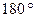,  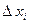и 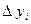 изменят знак, следовательно, интегральная сумма тоже изменит свой знак. Таким образом, криволинейный интеграл изменит знак на противоположный. В случае интеграла по замкнутому контуру L направление движения против часовой стрелки считается положительным.

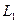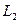2) Если линия L разделена на две части  и , то:

.

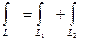Аналогичное утверждение справедливо для любого конечного числа частей.

Вычисление криволинейного интеграла

Пусть кривая L задана в параметрической форм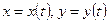е , где .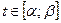

Тогда

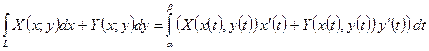.       (1)

В частном случае, если кривая L задана в декартовых координатах 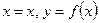, где 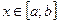, формула (1) имеет следующий вид:

.          (2)

Примеры:

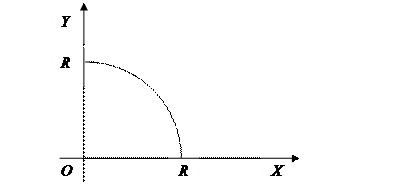
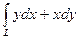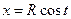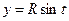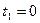1) Вычислить , где L – четверть окружности ,  от  до .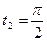

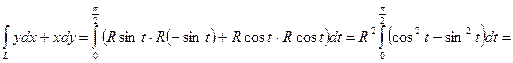
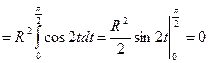
2) Вычислить 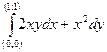 вдоль линии 1) y=x; 2) .

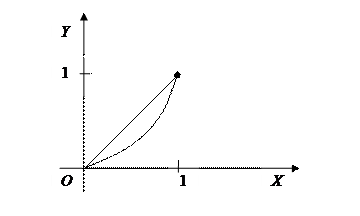
1)

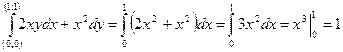
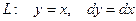
2)



  

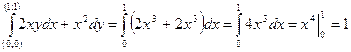
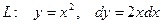
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.