- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение примеров
Решение примеров
а) 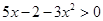
умножим на (–1)
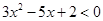
квадратное неравенство
Найдем корни уравнения 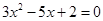
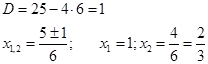
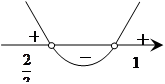
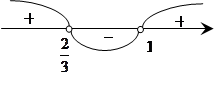
Графиком функции  является парабола, ветви которой направлены вверх, а точки пересечения параболы и оси OX
является парабола, ветви которой направлены вверх, а точки пересечения параболы и оси OX 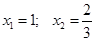
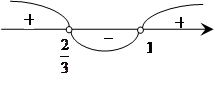 Изобразим геометрически:
Изобразим геометрически:
 |
или
 |
или
получаем три интервала, в которых определяем знак трехчлена. Так как мы решаем неравенство 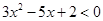 , то решением неравенства будет промежуток (интервал)
, то решением неравенства будет промежуток (интервал) 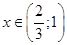
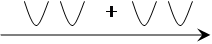
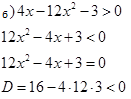
действительных корней нет, так как ветви параболы направлены вверх, то парабола не пересекает ось и расположена выше её, где всегда > 0,
а мы решаем неравенство 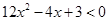 , значит данное неравенство не имеет решения.
, значит данное неравенство не имеет решения.
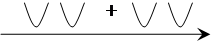
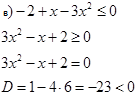
уравнение не имеет действительных корней, т.е. парабола не пересекает ось, ветви параболы направлены вверх,
а так как мы решаем неравенство 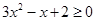 , то оно имеет множество решений, т.е.
, то оно имеет множество решений, т.е. 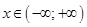 .
.
то оно имеет множество решений, т.е. е пересекает ось, ветви параболы направлены вверх, т.е. г) 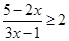 – дробно–рациональное неравенство, которое может быть решено или через системы неравенств или методом интервалов. Перенесем правую часть в левую, приведем подобные члены
– дробно–рациональное неравенство, которое может быть решено или через системы неравенств или методом интервалов. Перенесем правую часть в левую, приведем подобные члены
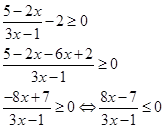
Решим через системы неравенств. Дробь < 0, если числитель и знаменатель имеют разные знаки, т.е.
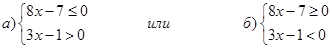
(Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю).
При решении системы неравенств надо решить каждое неравенство и выбрать общие промежутки.
Решаем 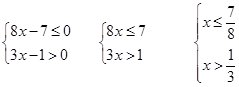

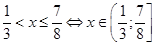
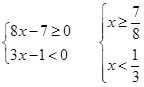
система не имеет решения. Следовательно решением данного неравенства является  .
.
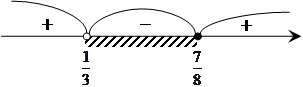 Метод интервалов позволяет ускорить процесс решения неравенства
Метод интервалов позволяет ускорить процесс решения неравенства 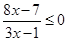 корни
корни 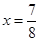 и
и 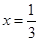 .
.

Метод интервалов позволяет решать не только неравенства II степени, дробно–рациональные но и более высоких степеней.
д) 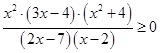 находим корни многочлена
находим корни многочлена
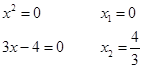
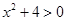 всегда, т.е. действительных корней нет.
всегда, т.е. действительных корней нет.
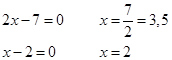
Отметим корни на числовой прямой, учитываем, что числитель может быть равен нулю.
только определяем знак выражения в каждом промежутке

|

|
| |
|
| |



|
|
|
|
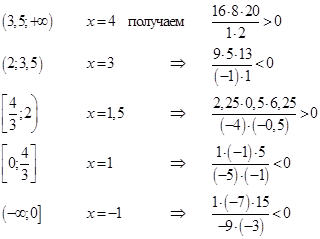
и тогда решением неравенства является 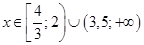 .
.
Можно несколько ускорить процесс определения знака в промежутках.
В промежутке больше большего корня всегда выражение больше нуля, а затем, если корень повторяется нечетное число раз (кратность его нечетная), то знаки в промежутках справа и слева от корня изменяются, а если кратность корня четная, то знак справа и слева от корня не изменяется.
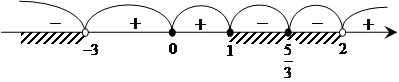 е)
е) 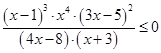
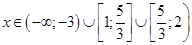 , так как
, так как 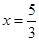 , то
, то 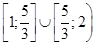 можно записать
можно записать 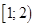
и тогда 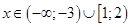
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|