ПОВТОРЕНИЕ: ПРОИЗВОДНАЯ

Здравствуйте, уважаемые студенты! Как-то вы не очень активно отправляете задания, а тем более делаете, рекомендую не списывать друг у друга ошибки, тем более ужасно глупые! Это всего лишь повторение пройденного материала, что вы должны знать! В ваших интересах сдать экзамен на хорошую оценку.

Сегодня отправляю лекцию для ознакомления, отправлять мне по ней ничего не надо, жду от вас долги.

ПОВТОРЕНИЕ: ПРОИЗВОДНАЯ

В предыдущей лекции мы повторили с вами таблицу производных, правила вычисления производной и вычисление производной для сложной функции.

Сегодня мы вспомним, а где и как применяется производная.

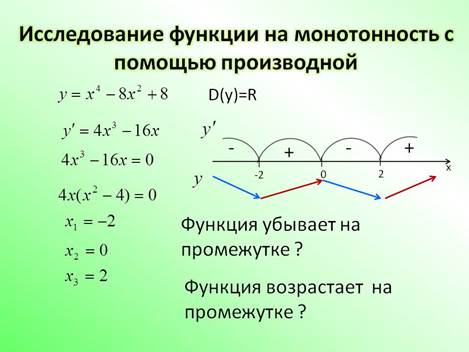
Производная применяется при определении монотонности функции, т.е. возрастание и убывание, мы можем определить, не строя график самой функции, а также экстремумы функции, т.е максимальное и минимальное значения функции и нахождение наибольшего и наименьшего значений функции.

На экзамене у вас как раз есть задание, связанное с производной, которое подразумевает нахождение: критических или стационарных точек, промежутки монотонности, экстремумы функции и нахождение наибольшего и наименьшего значения.

Итак, начинаем последовательно вспоминать

1. Стационарные точки – это точки, в которых производная равна нулю.

Критические точки – это точки, в которых производная не существует.

Для того, чтобы найти эти точки, нам необходимо сначала найти производную данной функции, а затем прировнять ее к нулю и решить уравнение, корни данного уравнения и будут стационарные или критические точки.

2. Промежутки монотонности

Итак, точки нашли, они нам пригодятся при определении промежутков монотонности. Данные точки расставляем на числовой прямой и определяем промежутки монотонности, т.е. определяем знаки на промежутках «+» или «-« между точками. Если промежуток имеет знак «+» - функция возрастает, если «-« - функция убывает.

ВАЖНО: при определении знаков, значения из промежутков подставляем в выражение производной!!!

3. Экстремумы функции

Итак, научились определять точки, промежутки монотонности и теперь по этим данным определим экстремумы функции ( )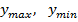

Экстремумы функции – это точки перехода с «+» на «-« и наоборот, т.е. точки перехода возрастания функции на убывание и наоборот.

ВАЖНО: для того, чтобы найти точку 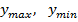, необходимо, стационарную точку (которую мы нашли при решении уравнения) подставить в первоначальную функцию, а не в выражение производной!!!

4. Наибольшее и наименьшее значения функции

И последний этап, нахождение наибольшего и наименьшего значения функции на определенном промежутке.

Для этого будем использовать стационарные точки (которые нашли при решении уравнения) и концы отрезков из промежутка.

В первоначальную функцию подставим все значения и вычислим значение функции, т.е посчитаем у, а затем выберем самое большое и самое маленькое значение, которое и будет определяться как у_наим, у_наиб.

ВАЖНО: проверяем какие стационарные точки входят в промежуток, только те и берем для подстановки!!!

А теперь рассмотрим один общий пример на каждое задание (аналогичный будет на экзамене)

Пример: Дана функция 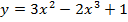. Найдите:

a) Стационарные или критические точки

b) Промежутки возрастания и убывания

c) Экстремумы функции

d) Наибольшее и наименьшее значения функции на отрезке [-1;4]

найдем производную функции

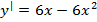
прировняем производную к нулю

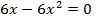
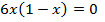
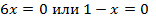
определяем знаки на каждом промежутке, для примера возьмем числа:

из левого промежутка -1, подставляем в выражение производной

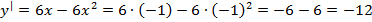
в центре 0,5, подставляем

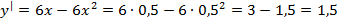
из правого промежутка

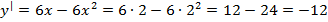
добавляем на чертеж

промежутки монотонности:

- функция возрастает: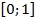

- функция убывает: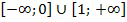

есть переход с «-« на «+» в точке 0 и с «+» на «-« в точке 1, следовательно, есть экстремумы:

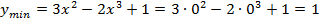
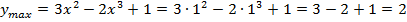
И последнее определяем у_наим, у_наиб

Проверяем: точки 0 и 1 входят в промежуток [-1;4]? Ответ: да, значит будем искать все 4 значения функции, но при вычислении экстремумов мы уже посчитали

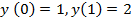
поэтому вычислим только:

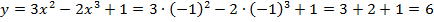
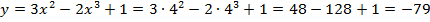
тогда у_наим=-79, а у_наиб=6