
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Указания к решению основных задач
Указания к решению основных задач
§ 1
1.Множество альтернатив – площадки около города, где постройка аэропорта нужного размера представляется возможной. Возможные критерии для оценки вариантов расположения аэропорта:
1) стоимость постройки. Желательно построить аэропорт с заданной пропускной способностью за наименьшую возможную цену.
2) расстояние от города. Желательно, чтобы поездка пассажиров от аэропорта в город и обратно занимала наименьшее время.
3) минимальное шумовое воздействие. Количество людей, подвергающихся нежелательным шумовым воздействиям, должно быть минимально.
2.Данная задача относится к задаче выбора наилучшей альтернативы. Заранее неизвестно, какие студенты подадут заявки. Множеством альтернатив является множество студентов г. Воронежа, подавших заявки на участие в конкурсе до определенного срока. Возможный вариант принципа оптимальности – премирование студента, обладающего высоким уровнем интеллектуальных способностей, достигшего наибольших, по мнению экспертов, успехов в исследовании экономических проблем региона, способного оперативно решать экономические задачи.
В соответствии с выбранным принципом оптимальности холдинг «A&A» принял решение провести испытание в три этапа.
Первый этап – тестирование общих интеллектуальных способностей участников. На этом этапе решается задача выбора из множества W нескольких альтернатив (студентов) в соответствии со следующим принципом: число перешедших во второй тур не должно превышать m, число набранных по тесту баллов каждым из студентов должно быть не ниже n. Результатом выбора является формирование 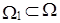 .
.
Второй этап – оценка реферата, посвященного экономическим проблемам региона. Работы оцениваются членами жюри (экспертами) по следующим критериям: 1) научная новизна и актуальность (в т.ч. соответствие проблематике); 2) обоснованность (реалистичность) полученных результатов; качество работы (используемый аппарат, оформление и т.п.); 3) наличие практических рекомендаций, их обоснованность и региональная направленность; 4) ожидаемая для региона эффективность внедрения полученных результатов.
Экспертами даны количественные оценки работ по каждому критерию  (
( 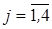 ), определены приоритеты критериев
), определены приоритеты критериев 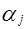 . В качестве ОП может быть использован принцип максимизации суммарной оценки проектов:
. В качестве ОП может быть использован принцип максимизации суммарной оценки проектов:
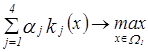 . На основе данного принципа отбирается группа финалистов.
. На основе данного принципа отбирается группа финалистов.
Третий этап – деловая игра, по результатам которой выявляется победитель испытания, набравший наибольшее количество очков.
§ 2
1.В отношение R входят пары элементов 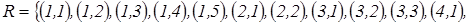

Матрица смежности для отношения R:
 .
.
Нижние сечения элементов:  ,
, 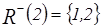 ,
, 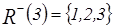 ,
, 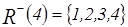 ,
, 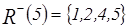 .
.
Верхние сечения элементов: 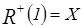 ,
, 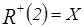 ,
, 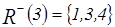 ,
, 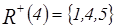 ,
, 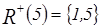 .
.
2. Для доказательства п. 1) достаточно доказать, что если 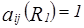 , то
, то  и если
и если 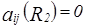 , то
, то 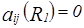 .
.
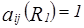
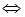
 , а так как
, а так как 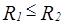 , то
, то 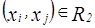
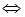
 , что и требовалось доказать. Аналогично доказывается второе условие.
, что и требовалось доказать. Аналогично доказывается второе условие.
1) Докажем, что 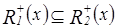 .
.
Рассмотрим 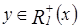 , следовательно,
, следовательно, 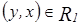 , а так как
, а так как  , то
, то 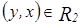 , а значит,
, а значит,  , т.е.
, т.е. 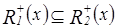 .
.
Аналогично доказывается, что 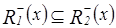 .
.
3.Докажем, что 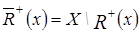 .
.
Пусть 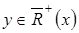
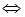
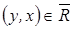
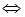
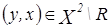
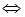
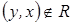
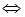
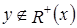
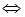
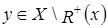 , то есть
, то есть 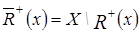 .
.
Равенство 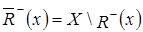 доказывается аналогично.
доказывается аналогично.
4. 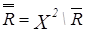 =
= 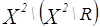 =R.
=R.
Аналогично в матричном виде: 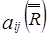 =1-
=1- 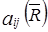 =1-1-(-
=1-1-(- 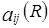 )=
)= 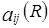 .
.
5. Докажем, что 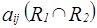 =
= 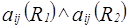 .
.
Рассмотрим 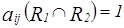
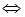

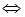

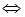
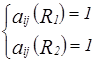
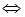
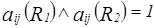 .
.
Если 
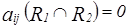 , то это равносильно тому, что
, то это равносильно тому, что 
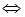
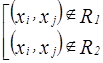
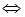

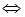
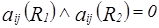 .
.
Следовательно, 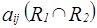 =
= 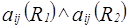 .
.
п. 2) доказывается аналогично п.1.
6. 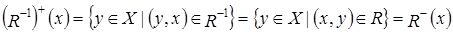 . Аналогично доказывается и вторая формула.
. Аналогично доказывается и вторая формула.
7.Докажем, что 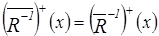 .
.
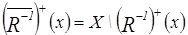 =
= 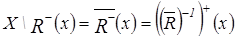 , что и требовалось доказать.
, что и требовалось доказать.
8. Пусть 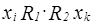 . Покажем, что в этом случае
. Покажем, что в этом случае 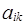 =1.
=1.
По определению произведения 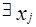 :
:  и
и 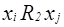 , то есть,
, то есть, 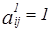 ,
, 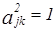
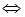

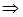
 .
.
Пусть  , тогда хотя бы одно слагаемое в формуле (*) равно 1, т.е. существует
, тогда хотя бы одно слагаемое в формуле (*) равно 1, т.е. существует  . Тогда
. Тогда 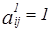 ,
, 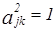
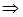
 и
и 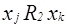 , т.е.
, т.е. 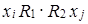 , что и требовалось доказать.
, что и требовалось доказать.
9.Рассмотрим формирование элемента 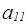 матрицы
матрицы 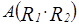 .
.
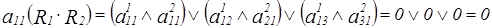 .
.
Аналогично: 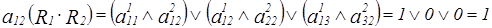 .
.
Аналогично формируются остальные элементы матрицы. Итоговая матрица имеет вид:
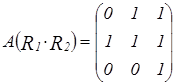 .
.
10. Предположим, что R симметрично. Докажем, что 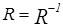 .
.
Так как 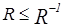 по определению симметричного отношения, то достаточно показать, что
по определению симметричного отношения, то достаточно показать, что 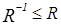 .
.
Рассмотрим 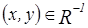
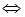
 , тогда в силу симметричности R
, тогда в силу симметричности R 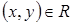 , следовательно,
, следовательно, 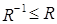 .
.
Обратно, если  , то
, то 
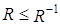 , следовательно, R – симметрично.
, следовательно, R – симметрично.
11. Предположим противное: R не является антирефлексивным. Тогда существует 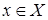 такое, что
такое, что 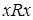 . Из определения обратного отношения это эквивалентно тому, что
. Из определения обратного отношения это эквивалентно тому, что  , следовательно,
, следовательно, 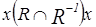 , т.е.
, т.е.  Æ, что противоречит асимметричности R.
Æ, что противоречит асимметричности R.
12. 1) Для точки a отношения 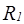 выполнено:
выполнено: 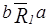 ,
,  ,
, 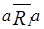 , следовательно, a – мажоранта данного отношения. Аналогично b- миноранта (
, следовательно, a – мажоранта данного отношения. Аналогично b- миноранта ( 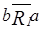 ,
,  ,
,  ). Точка c не является мажорантой, так как
). Точка c не является мажорантой, так как 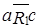 не выполнено, и не является минорантой, так как
не выполнено, и не является минорантой, так как 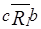 не выполнено. Максимумов и минимумов у данного отношения нет.
не выполнено. Максимумов и минимумов у данного отношения нет.
2) Мажорантами отношения 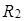 являются a и c, так как
являются a и c, так как  ,
, 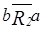 ,
, 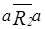 и
и 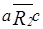 ,
, 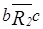 ,
, 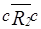 . Аналогично b- миноранта.
. Аналогично b- миноранта.
3) Точка a является максимумом, так как 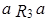 ,
, 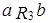 ,
, 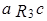 . Элементы b,c – миноранты.
. Элементы b,c – миноранты.
13. Пусть R – отношение частичного порядка.
Предположим противное: существуют два максимума по отношению R: 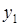 и
и 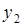
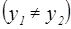 . Тогда
. Тогда  ,
, 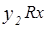 для любого
для любого 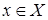 . Следовательно,
. Следовательно,  и
и  . Так как R – антисимметрично, то
. Так как R – антисимметрично, то 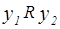 и
и 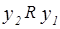 тогда и только тогда, когда
тогда и только тогда, когда 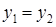 , получили противоречие. Следовательно, максимум по частичному порядку единственен.
, получили противоречие. Следовательно, максимум по частичному порядку единственен.
Для произвольного R данное утверждение не всегда верно. Например, рассмотрим R:
 |
 a b . Точки a, b – максимумы.
a b . Точки a, b – максимумы.
c
14. Предположим противное: пусть a – максимум по отношению R, b- мажоранта.
a – максимум по отношению R, тогда 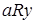 ,
, 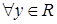 . Следовательно,
. Следовательно, 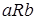 ;
;
b – мажоранта, тогда 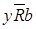 ,
, 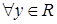 . Следовательно,
. Следовательно, 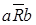 . Тогда
. Тогда 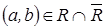 и, следовательно,
и, следовательно, 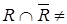 Æ. Но так как по определению
Æ. Но так как по определению 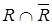 =Æ, то получили противоречие, следовательно, максимумы и мажоранты одновременно существовать не могут. Аналогично доказывается п. 2).
=Æ, то получили противоречие, следовательно, максимумы и мажоранты одновременно существовать не могут. Аналогично доказывается п. 2).
15. 1) Пусть 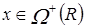 . Тогда
. Тогда 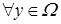 :
:  . Это равносильно тому, что выполнено
. Это равносильно тому, что выполнено 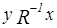 , следовательно,
, следовательно, 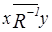 - не выполнено. Из последнего следует, что не выполнено
- не выполнено. Из последнего следует, что не выполнено 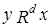 . Это эквивалентно тому, что
. Это эквивалентно тому, что 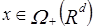 . Таким образом,
. Таким образом, 
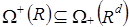 .
.
Аналогично доказывается п.2).
§ 3
1.Опишем каждое из перечисленных в условии бинарных отношений, воспользовавшись определением сужения и двойственного отношения:
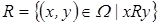 , тогда
, тогда  ,
,  .
.
С другой стороны:  , тогда
, тогда 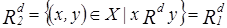 , что и требовалось доказать.
, что и требовалось доказать.
2.Докажем п. 1). Для доказательства воспользуемся задачей 15 § 2 и задачей 1 § 3. Рассмотрим 
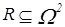 ,
, 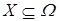 ,
, 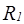 ,
, 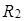 - определяемые, как и в задаче 1 из §2.
- определяемые, как и в задаче 1 из §2.  , тогда в силу произвольности выбора множества X получаем, что
, тогда в силу произвольности выбора множества X получаем, что 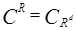 . Пункт 2) доказывается аналогично.
. Пункт 2) доказывается аналогично.
3.Рассмотрим 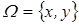 . Бинарные отношения
. Бинарные отношения 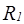 и
и 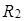 (
( 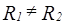 ) зададим графами:
) зададим графами:
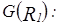
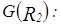

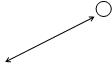 y
y
 |
y
x
x
Построим функцию 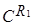 , определив ее на каждом из подмножеств
, определив ее на каждом из подмножеств 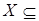
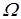 .
.
a) 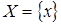 .
. 
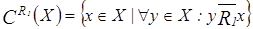 .Так как
.Так как 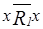 , то
, то  .
.
b)  . Так как
. Так как 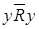 не выполнено, то
не выполнено, то 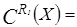 Æ;
Æ;
c)  . Так как
. Так как 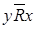 не выполнено, то
не выполнено, то 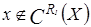 ; так как
; так как 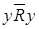 не выполнено, то
не выполнено, то 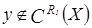 . Следовательно,
. Следовательно, 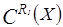 =Æ.
=Æ.
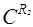 строится аналогично:
строится аналогично:
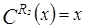 ,
, 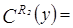 Æ,
Æ, 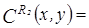 Æ.
Æ.
Таким образом, 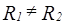 , но
, но 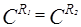 .
.
4.Рассмотрим функцию выбора, определяемую на подмножествах множества  следующим образом:
следующим образом: 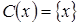 ,
, 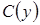 =Æ,
=Æ,  .
.
Предположим противное: существует отношение  такое, что
такое, что 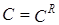 . Построим данное отношение.
. Построим данное отношение.
a) 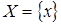 .
. 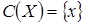 . Следовательно, для любого элемента
. Следовательно, для любого элемента  выполнено:
выполнено:  , т.е.
, т.е. 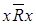 .
.
b)  .
. 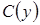 =Æ, следовательно, в множестве
=Æ, следовательно, в множестве 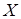 не существует элемента
не существует элемента 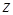 такого, что
такого, что  ,
, 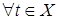 , т.е.
, т.е. 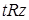 для любого
для любого  . Следовательно,
. Следовательно, 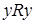 .
.
c)  .
.  , следовательно,
, следовательно, 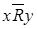 ,
, 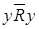 , но из п.b) следует, что для R должно быть выполнено
, но из п.b) следует, что для R должно быть выполнено 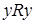 . Получили противоречие. Следовательно, такого отношения R не существует и функция выбора не является нормальной.
. Получили противоречие. Следовательно, такого отношения R не существует и функция выбора не является нормальной.
Заметим, что аналогично можно доказать, что не существует такого бинарного отношения R, что 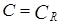 .
.
5.1) Для функции 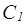 построим
построим 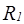 :
: 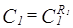 .
.
a) 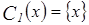 :
: 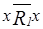 ;
;
b) 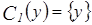 :
:  ;
;
c)  :
: 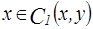
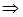
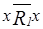 ,
, 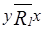 ;
;
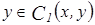
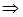
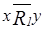 ,
,  .
.
Граф отношения 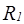 имеет вид:
имеет вид:
 y
y
 x
x
Построим 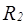 :
: 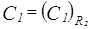 .
.
a) 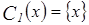 :
: 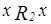 ;
;
b) 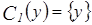 :
:  ;
;
c)  :
: 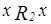 ,
,  ;
; 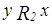 ,
,  .
.
Граф отношения 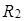 имеет вид:
имеет вид:
 |
x y
2) Для функции 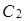 построим
построим 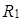 :
: 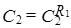 .
.
a) 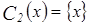 :
: 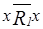 ;
;
b) 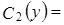 Æ:
Æ: 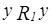 ;
;
c) 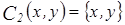 :
: 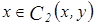
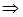
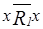 ,
, 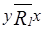 ;
;
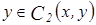
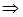
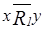 ,
,  . Но
. Но 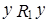 из п. b). Отношение
из п. b). Отношение 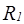 и, следовательно,
и, следовательно, 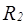 построить невозможно, данная функция не является нормальной.
построить невозможно, данная функция не является нормальной.
1) Для функции 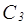 построим
построим 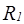 :
: 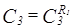 .
.
a)  :
: 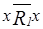 ;
;
b) 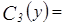 Æ:
Æ: 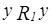 ;
;
c) 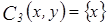 :
: 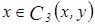
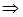
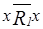 ,
, 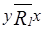 ;
;
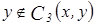
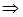
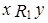 или (и)
или (и) 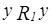 . Но так как
. Но так как 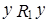 из п.b), то
из п.b), то 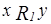 может как выполняться, так и не выполняться. В силу этого в качестве
может как выполняться, так и не выполняться. В силу этого в качестве 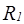 можно рассмотреть одно из следующих бинарных отношений:
можно рассмотреть одно из следующих бинарных отношений:
 |
 (
( 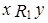 выполнено)
выполнено)
x y


 (
( 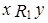 не выполнено)
не выполнено)
x y
Аналогично строится 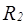 :
:
a)  :
: 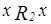 ;
;
b)  =Æ:
=Æ:  ;
;
c)  :
: 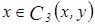
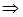
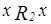 ,
,  ;
;
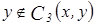
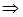
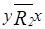 и (или)
и (или) 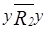 . Но так как
. Но так как  из п.b), то
из п.b), то 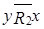 может как выполняться, так и не выполняться. В силу этого в качестве
может как выполняться, так и не выполняться. В силу этого в качестве 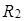 можно рассмотреть одно из следующих бинарных отношений:
можно рассмотреть одно из следующих бинарных отношений:
 |
 (
( 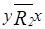 выполнено)
выполнено)
x y
 (
( 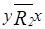 не выполнено)
не выполнено)

x y
6. Воспользуемся алгоритмом 1, записав шаги 1 и 2 в виде таблицы:
| X | C(X) | 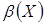
| 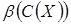
|
| x | Æ | ||
| y | y | ||
| z | z | ||
| x, y | y | ||
| x, z | z | ||
| y, z | y | ||
| x, y, z | y |
Найдем функцию 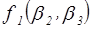 :
:
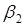
| 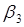
| 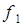
|
Найдем  . Рассмотрим набор
. Рассмотрим набор 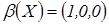 , т.е.
, т.е. 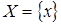 ;
; 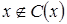
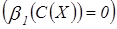 , следовательно,
, следовательно, 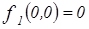 .
.
Аналогично определяются остальные значения функции. Таким образом, 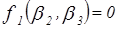 .
.
Найдем функцию 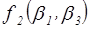 :
:

| 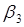
| 
|
Найдем 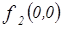 . Рассмотрим набор
. Рассмотрим набор 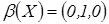 , т.е.
, т.е.  ;
; 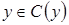
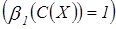 , следовательно,
, следовательно, 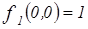 .
.
Аналогично определяются остальные значения функции. Таким образом, 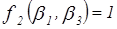 .
.
Аналогичную таблицу сформируем для 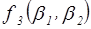 :
:

| 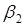
| 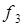
|
Таким образом, 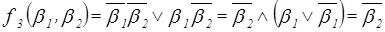 .
.
Логическая форма функции выбора: 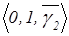 .
.
7.Переобозначим аргументы функций 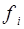 ,
, 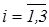 :
: 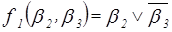 ,
, 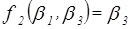 ,
, 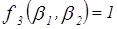 . Полученные функции сведем в таблицы:
. Полученные функции сведем в таблицы:
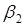
| 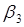
| 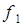
|

| 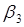
| 
|

| 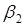
| 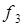
|
Для определения функции выбора C(X) воспользуемся формулой (4), составив таблицу:
| X | 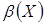
| 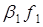
| 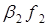
| 
| C(X) |
| x | x | ||||
| y | Æ | ||||
| z | z | ||||
| x, y | x | ||||
| x, z | z | ||||
| y, z | y, z | ||||
| x, y, z | x, y, z |
Рассмотрим формирование подмножества 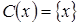 . Рассмотрим множество
. Рассмотрим множество 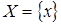 ,
, 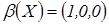 . Найдем
. Найдем 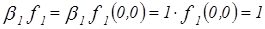 . Следовательно,
. Следовательно, 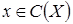 . Аналогично формируются остальные элементы таблицы.
. Аналогично формируются остальные элементы таблицы.
8. Значения функций выбора 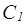 ,
, 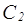 , а также
, а также 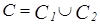 ,
,  ,
,  ,
, 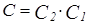 выпишем в следующую таблицу.
выпишем в следующую таблицу.
| X | 
| 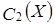
| 
| 
| 
| 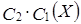
|
| x | Æ | x | x | Æ | x | Æ |
| y | y | Æ | y | Æ | Æ | Æ |
| z | z | z | z | z | Æ | z |
| x, y | y | x | x, y | Æ | x | Æ |
| x, z | z | z | z | z | x | z |
| y, z | y | y, z | y, z | y | z | Æ |
| x,y,z | y | x,y,z | x, y, z | y | x, z | Æ |
Рассмотрим процедуру формирования первой строки таблицы для множества 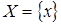 :
:
1) 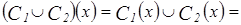 Æ
Æ 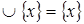 ;
;
2) 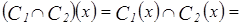 Æ
Æ 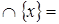 Æ;
Æ;
3) 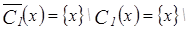 Æ=
Æ= 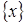 ;
;
4) 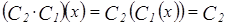 (Æ)=Æ.
(Æ)=Æ.
Для нахождения ЛФВ построенных функций воспользуемся теоремой 1 и теоремой 2. Из задач 6 и 7 п. 3 :
ЛФВ ( 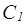 )=
)=  ; ЛФВ (
; ЛФВ ( 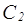 )=
)= 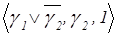 . Тогда:
. Тогда:
1) Найдем ЛФВ ( 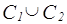 ).
).
 ;
;
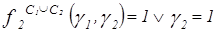 ;
;
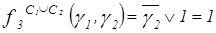 .
.
ЛФВ ( 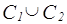 )=
)=  ;
;
2) Найдем ЛФВ (  ).
).
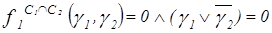 ;
; 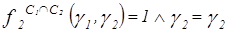 ;
; 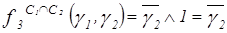 . ЛФВ (
. ЛФВ (  )=
)= 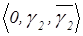 .
.
3) Найдем ЛФВ ( 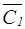 ).
).
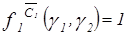 ;
; 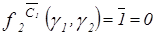 ;
; 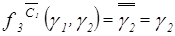 .
.
ЛФВ ( 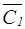 )=
)= 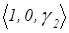 .
.
4) Найдем ЛФВ ( 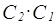 ).
).
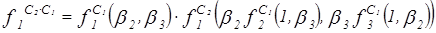 =
=
= 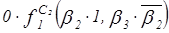 =0;
=0;
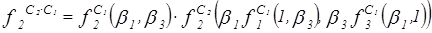 =
=
= 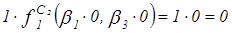 ;
;
 =
=
= 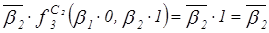 . ЛФВ (
. ЛФВ ( 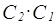 )=
)= 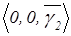 .
.
9.Докажем, что если 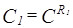 ,
, 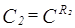 , то
, то  .
.
Рассмотрим 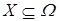 (
( 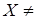 Æ).
Æ).
Рассмотрим 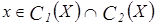 . Тогда
. Тогда 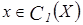 ,
, 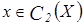 и для всех
и для всех 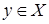 выполнено:
выполнено:
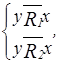
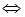
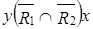
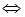

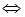
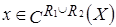 .
.
Таким образом, доказано, что  существует бинарное отношение
существует бинарное отношение 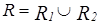 такое, что
такое, что 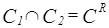 , т.е.
, т.е.  - нормальная функция выбора.
- нормальная функция выбора.
10.1. Докажем, что условие наследования выполнено.
Рассмотрим 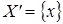 ,
,  .
. 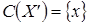 ;
;  , тогда
, тогда 
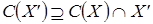 .
.
Рассмотрим 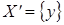 ,
, 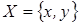 .
. 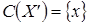 ;
; 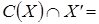 Æ, тогда
Æ, тогда 
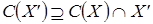 .
.
2.Докажем, что условие независимости от отвергнутых альтернатив выполнено. Для этого достаточно рассмотреть множества 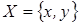 ,
, 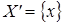 :
:  и
и 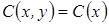 .
.
3. Условие согласия выполнено, так как 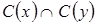 =Æ, что является подмножеством множества
=Æ, что является подмножеством множества 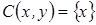 .
.
4. Условие Плотта выполнено, так как:
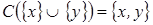 и
и 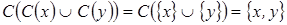 ;
;
 и
и 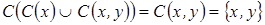 . Аналогично свойство выполняется для множеств
. Аналогично свойство выполняется для множеств  и
и  .
.
5.Условие сумматорности не выполнено.
Рассмотрим