
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Отчет по практическим работам. ОПРЕДЕЛЕНИЕ НАДЕЖНОСТИ СИСТЕМ РАЗЛИЧНЫХ СТРУКТУР ». Вариант 3
МИНОБРНАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
Кафедра «Сервиса и эксплуатации транспортных и
технологических машин»
Отчет по практическим работам
«ОПРЕДЕЛЕНИЕ НАДЕЖНОСТИ СИСТЕМ РАЗЛИЧНЫХ СТРУКТУР »
Вариант 3
Выполнил:
Студент группы АМС-41 Ермолаев И.Е.
Шифр 45612
Проверил: Новоселов В.Г.
Екатеринбург
Задача 1. Определить конструкционную надежность агрегата для интервала времени t со следующим средними статистическими данными об интенсивности отказов основных его частей в долях единицы на 1 ч работы: 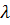 1= 0,01
1= 0,01  10-6,
10-6, 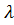 2=0,05
2=0,05  10-6,
10-6, 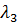 =0,4
=0,4  10-6,
10-6, 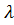 4=3
4=3  10-6,
10-6, 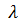 5=1
5=1  10-6, ч-1
10-6, ч-1
Основные части агрегата соединены последовательно, а величины их надежности изменяются во времени по экспоненциальному закону.
Исходные данные по вариантам
| Вариант | ||||||||||
t, ч  103 103
|
Решение проводится в следующей последовательности:
1. Определяется средняя результирующая интенсивность отказов всех основных частей агрегата, ч-1
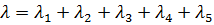 =0,01
=0,01  10-6+0,05
10-6+0,05  10-6+0,4
10-6+0,4  10-6+3
10-6+3  10-61
10-61  10-6
10-6
=4,46  10-6 ч-1
10-6 ч-1
2. Средняя наработка до первого отказа агрегата, ч
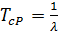 = 224215 ч
= 224215 ч
3. Вероятность безотказной работы, или конструкционная надежность, рассматриваемого агрегата для интервала времени t составит
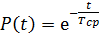 =
= 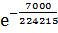 =0,97
=0,97
4 Вероятность отказа агрегата определяется по формуле
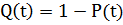 =0,03
=0,03
По полученным данным необходимо определить на каждые 1000 агрегатов вероятность выхода из строя в течение заданного времени работы в количественном и процентном соотношении.
𝑛вышед. из строя=𝑄(𝑡)∙𝑛общ=0,03∙1000=30
(30/1000)*100%=3%
Задача 2. Оценить вероятность безотказной работы редуктора, если условные запасы прочности по средним значениям несущей способности и нагрузки составляют: для зубчатой передачи 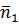 = 1,5; для подшипников входного вала
= 1,5; для подшипников входного вала 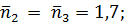 для подшипников выходного вала
для подшипников выходного вала 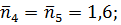 выходного и входного валов
выходного и входного валов 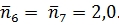 Это соответствует математическим ожиданиям несущей способности элементов mR1= 1,5mF; mR2 = mR3 = 1,7mF; mR4 = mR5 = 1,6mF; mR6 = mR7 = 2mF. Задано, что несущие способности передачи, подшипников и валов нормально распределены с одинаковыми коэффициентами вариации
Это соответствует математическим ожиданиям несущей способности элементов mR1= 1,5mF; mR2 = mR3 = 1,7mF; mR4 = mR5 = 1,6mF; mR6 = mR7 = 2mF. Задано, что несущие способности передачи, подшипников и валов нормально распределены с одинаковыми коэффициентами вариации 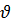 R, а нагрузка по редуктору распределена также нормально с коэффициентом вариации
R, а нагрузка по редуктору распределена также нормально с коэффициентом вариации 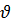 F. Нагрузки FA и FB приняты в предположении, что эти значения близки к требуемым значениям вероятностей безотказной работы систем при фиксированных нагрузках P (R
F. Нагрузки FA и FB приняты в предположении, что эти значения близки к требуемым значениям вероятностей безотказной работы систем при фиксированных нагрузках P (R 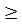 FA) и P (R
FA) и P (R 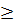 FB).
FB).
При определении квантилей UPA и UPB и вероятности безотказной работы P (R ≥ FА) и P (R ≥ FВ) используют метод экстраполирования полученных значений на соответствующем интервале. Все расчеты необходимо вести до четвертого знака после запятой.
Исходные данные по вариантам
| Вариант | ||||||||||
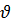 R R
| 0,10 | 0,11 | 0,12 | 0,13 | 0,14 | 0,15 | 0,14 | 0,13 | 0,12 | 0,11 |
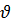 F F
| 0,10 | 0,11 | 0,12 | 0,13 | 0,14 | 0,15 | 0,13 | 0,12 | 0,11 | 0,10 |
| FA | 1,3 mF | 1,33 mF | 1,36 mF | 1,39 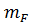
| 1,33 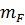
| 1,3 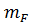
| 1,36 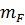
| 1,39 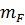
| 1,36 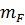
| 1,33 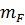
|
| FB | 1,1 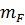
| 1,11 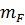
| 1,12 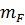
| 1,13 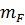
| 1,14 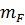
| 1,15 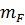
| 1,14 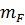
| 1,13 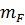
| 1,12 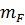
| 1,11 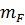
|
Решение проводится в следующей последовательности.
1. Вычисляются квантили нормального распределения всех элементов, соответствующие их вероятностям безотказной работы при нагрузках FA и FB.
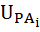 =
= 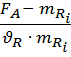 ;
; 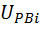 =
= 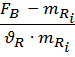 ,
,
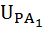 =
= 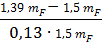 =-0,56
=-0,56 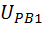 =
= 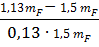 =-1,89
=-1,89
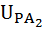 =
= 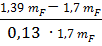 =-1,4
=-1,4 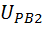 =
= 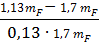 =-2,57
=-2,57
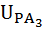 =
= 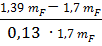 =-1,4
=-1,4  =
= 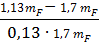 =-2,57
=-2,57
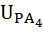 =
= 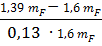 =-1,01
=-1,01 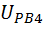 =
=  =-2,25
=-2,25
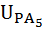 =
= 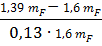 =-1,01
=-1,01 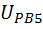 =
=  =-2,25
=-2,25
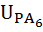 =
= 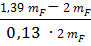 =-2,34
=-2,34 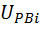 =
= 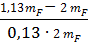 =-3,34
=-3,34
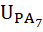 =
= 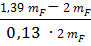 =-2,34
=-2,34 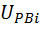 =
= 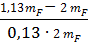 =-3,34
=-3,34
где i – номер элемента.
2. По квантилям из таблицы находится вероятность безотказной работы элементов
 при нагрузке FА
при нагрузке FА  P1 (R ≥ FА)= 0,7257
P1 (R ≥ FА)= 0,7257
Р2 = Р3 (R ≥ FА)= 0,9192
Р4 = Р5 (R ≥ FА)= 0,8413
Р6 = Р7 (R ≥ FА)= 0,99
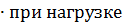 FВ
FВ
P1 (R ≥ FВ)= 0,97
Р2 = Р3 (R ≥ FВ)= 0,995
Р4 = Р5 (R ≥ FВ)= 0,9893
Р6 = Р7 (R ≥ FВ)= 0,9998
Значения квантили UP нормального распределения
| Квантиль UP | Вероятность безотказной работы P(t) | Квантиль UP | Вероятность безотказной работы P(t) | Квантиль UP | Вероятность безотказной работы P(t) | Квантиль UP | Вероятность безотказной работы P(t) |
| 0,000 | 0,5000 | - 0,8 | 0,7881 | - 1,7 | 0,9554 | - 2,5 | 0,9938 |
| - 0,1 | 0,5398 | - 0,842 | 0,80 | - 1,751 | 0,96 | - 2,576 | 0,995 |
| - 0,126 | 0,55 | - 0,9 | 0,8159 | - 1,8 | 0,9641 | - 2,6 | 0,9953 |
| - 0,2 | 0,5793 | - 1,0 | 0,8413 | - 1,881 | 0,97 | - 2,652 | 0,996 |
| - 0,253 | 0,60 | - 1, 036 | 0,85 | - 2,0 | 0,9772 | - 2,7 | 0,9965 |
| - 0,3 | 0,6179 | - 1,1 | 0,8643 | - 2,054 | 0,98 | - 2,748 | 0,997 |
| - 0,385 | 0,65 | - 1,2 | 0,08849 | - 2,1 | 0,9821 | - 2,8 | 0,9974 |
| - 0,4 | 0,6554 | - 1,282 | 0,90 | - 2,170 | 0,985 | - 2,878 | 0,998 |
| - 0,5 | 0,6915 | - 1,3 | 0,9032 | - 2,2 | 0,9861 | - 2,9 | 0,9981 |
| - 0,524 | 0,70 | - 1,4 | 0,9192 | - 2,3 | 0,9893 | - 3,0 | 0,9986 |
| - 0,6 | 0,7257 | - 1,5 | 0,9332 | - 2,326 | 0,99 | - 3,090 | 0,999 |
| - 0,674 | 0,75 | - 1,6 | 0,9452 | - 2,4 | 0,9918 | - 3,291 | 0,9995 |
| - 0,7 | 0,7580 | - 1,645 | 0,95 | - 2,409 | 0,992 | -3,5 | 0,9998 |
3. Вероятности безотказной работы редуктора P (R ≥ FА) и P (R ≥ FВ) оцениваются по формулам
P (R ≥ FА) = Р1 (R ≥ FА)  Р2,3 (R ≥ FА)
Р2,3 (R ≥ FА)  Р4,5 (R ≥ FА)
Р4,5 (R ≥ FА)  Р6,7 (R ≥ FА)=
Р6,7 (R ≥ FА)=
=0,7257*0,9192*0,9192*0,8413*0,8413*0,99*0,99=0,43
P (R ≥ FВ) = Р1 (R ≥ FВ) ∙ Р2,3 (R ≥ FВ) ∙ Р4,5 (R ≥ FВ) ∙ Р6,7 (R ≥ FВ)=
=0,97*0,995*0,995*0,9893*0,9893*0,9998*0,9998=0,939
4. По полученным значениям P (R ≥ FА) и P (R ≥ FВ) по таблице определяют квантили UPA и UPB
UPA=0
UPB=-1,6
1. Вычисляют математическое ожидание mR по формуле 
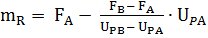 =1.39mf -
=1.39mf -  *( 0)= 1,39mf
*( 0)= 1,39mf
и коэффициент вариации
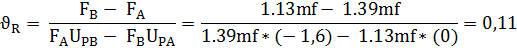
6. Рассчитывают квантиль UP нормального распределения, соответствующую вероятности P (R ≥ F) безотказной работы редуктора по формуле
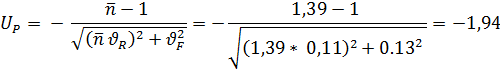
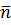 = mR / mF=1,39mf/mf=1,39
= mR / mF=1,39mf/mf=1,39
7. По таблице находится искомая вероятность, соответствующая полученной квантили.
P (R ≥ FА) = 0,9772
Задача3. В соответствии с затратами на ремонт узлов, представленными в таблице, провести структурный анализ и определить надежность машины в целом, принимая, что вероятность безотказной работы каждого из десяти узлов составляет Р = 0,95.
Исходные данные по вариантам
| Вариант | Затраты на капитальный ремонт ZKP | Коэффициент нормируемых затрат | Затраты на ремонт узлов Zi | |||||||||
|
0,35
| ||||||||||||
| 0,32 | ||||||||||||
| 0,45 | ||||||||||||
| 0,33 | ||||||||||||
ZKP=45
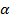 =0.32
=0.32
Z1=10 Z2=53 Z3=55 Z4=15 Z5=14 Z6=11 Z7=13 Z8=12 Z9=9 Z10=16
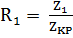 =0,22
=0,22 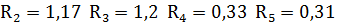
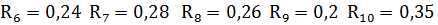
1,2>1,17>1>0,35>0,33> 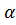 >0,31>0,28>0,26>0,24>0,22>0,2
>0,31>0,28>0,26>0,24>0,22>0,2
R3>R2>1>R10>r4>a>R5>R7>R8>R6>R1>R9
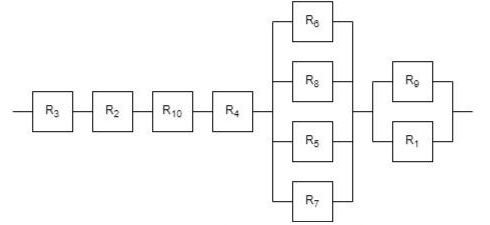
𝑃6−8−5−7=1−(1−𝑃6)(1−𝑃8)(1−𝑃5)(1−𝑃7)==1−(1−0,95)(1−0,95)(1−0,95)(1−0,95)=1−0,00000625==0,99999375
𝑃9−1=1−(1−𝑃9)(1−𝑃1)=1−(1−0,95)(1−0,95)=1−0,0025==0,9975 𝑃=𝑃3∙𝑃2∙𝑃10∙𝑃4∙𝑃6−8−5−7∙𝑃9−1==0,95∙0,95∙0,95∙0,95∙0,99999375∙0,9975=0,8125
.ЛИТЕРАТУРА
1. Шишмарев В.Ю. Надежность технических систем: учебник для студ. высш. учеб. заведений. – М.: Издательский центр «Академия», 2010.–304 с.
2. Решетов Д.Н. и др. Надежность машин: Учеб. пособие для машиностроительных специальностей вузов. – М.: Высш. шк., 1988. –152 с.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|