
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 50. Задача 51. Задача 52. Задача 53. Задача 54
Задача 50
Плотность моторного масла 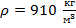 . Определить его удельный вес.
. Определить его удельный вес.
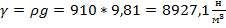 .
.
Задача 51
Определить количество теплоты, которое необходимо подвести к 3 кг воздуха, находящегося в закрытом сосуде и имеющего температуру t1=0oC и давление P1=0,1МПа, чтобы нагреть его до 500оС. Определить конечное давление, если внутренние энергий составляют: U1=194,8 кДж/кг; U2=570,5 кДж/кг.

Задача 52
Определить количество подведенной теплоты и работу, совершаемую 2 кг азота (N2)при его изобарном нагревании от 100 до 600оС, если давление P1=1МПа и h1=387,3 кДж/кг, h2=929,0 кДж/кг.
Задача 53
Определить работу, затрачиваемую на адиабатное сжатие 5 кг воздуха, и его конечное давление, если при этом температура увеличивается от 0 до 300оС, начальное давление Р1=0,1 МПа, и U1=194,8 кДж/кг, U2=414,4 кДж/кг.
Количество работы определяется
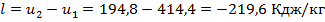 . Знак минус указывает, что для сжатия воздуха нужно затратить работу.
. Знак минус указывает, что для сжатия воздуха нужно затратить работу.
Полная работа определяется
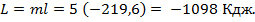
Для расчета конечного давления 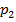 нужно воспользоваться формулой с показателем адиабаты нужно принимать
нужно воспользоваться формулой с показателем адиабаты нужно принимать 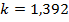 для воздуха.
для воздуха.
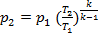 =
= 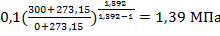
Задача 54
В процессе политропного расширения воздуха его температура уменьшается от t1 = 25 ºC до t2 = – 37 ºC. Начальное давление воздуха Р1 = 4 бара, количество воздуха m = 2 кг. Определить изменение энтропии в этом процессе, если известно, что количество подведенного к воздуху тепла составляет 89,2 кДж,  .
.
Решение:
Количество тепла, сообщаемого в политропном процессе составляет:
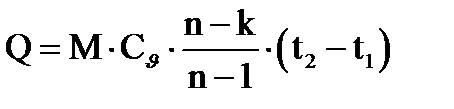
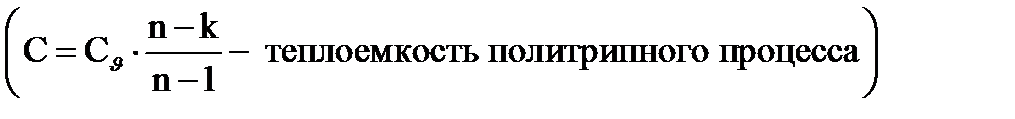
Подставляя значения известных величин получаем:
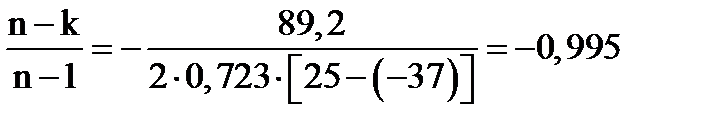

Из соотношения параметров политропного процесса определяем конечное давление:
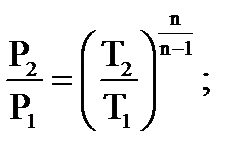
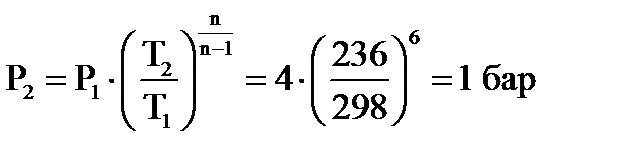
Изменение энтропии по соотношению:
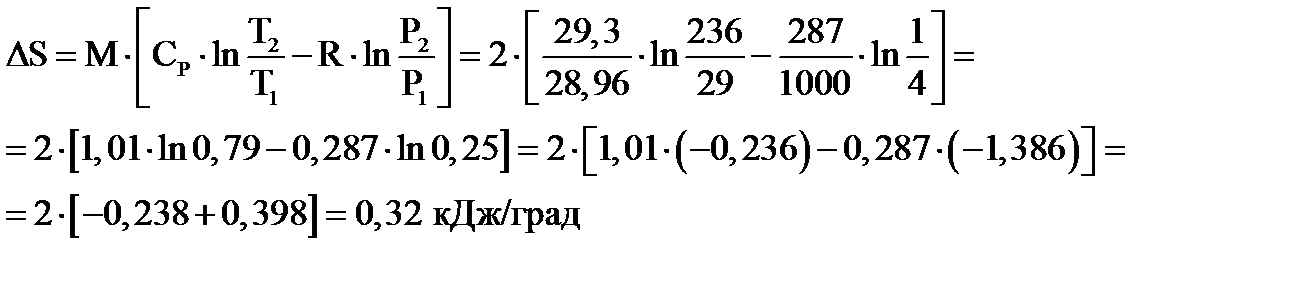
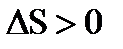
Задача 55.В результате осуществления кругового процесса получена полезная работа 70 кДж, и отдано холодильнику (теплообменнику) 42 кДж. Определить ηt цикла.
Решение:
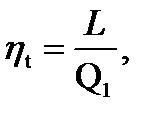
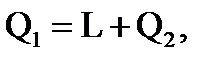
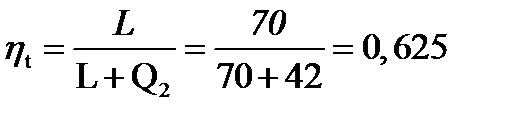
Задача 56.Один килограмм воздуха совершает цикл Карно между двумя температурами t1 = 327 ºC и t2 = 27 ºC. Количество тепла, отводимое в холодильник (теплообменник) 35 кДж/кг. Определить q1 (теплоту теплоотдатчика).
Решение:
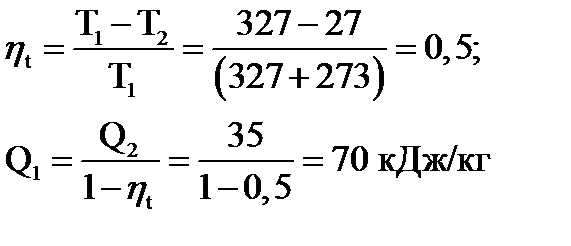
Задача 57.Определить термический КПД газовой турбины, с подводом теплоты по изохоре и температуру Т3, если даны: Р1 = 1 бар; t1 = 0 ºС; Р2 = 9 бар; Р3 = 13 бар (давления абсолютные); рабочее тело – 1 кг сухого воздуха.
Решение:
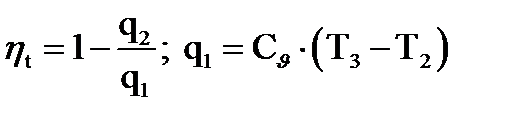


Задача 58.Градиент температуры в детали составляет 200 град/м; коэффициент теплопроводности материала 210 Вт/м∙К. Определить плотность теплового потока.
Решение:
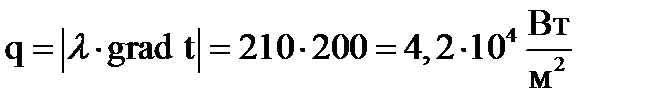
Задача 59.Вычислить средний коэффициент теплопередачи при поперечном обтекании воздухом плоской трубы сечением 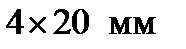 . Скорость воздуха 30 м/с, его температура t = 100 ºС, кинематическая вязкость ν = 23,13·10-6 м2/с, теплопроводность λ = 0,0321 Вт/м·К.
. Скорость воздуха 30 м/с, его температура t = 100 ºС, кинематическая вязкость ν = 23,13·10-6 м2/с, теплопроводность λ = 0,0321 Вт/м·К.
Решение:

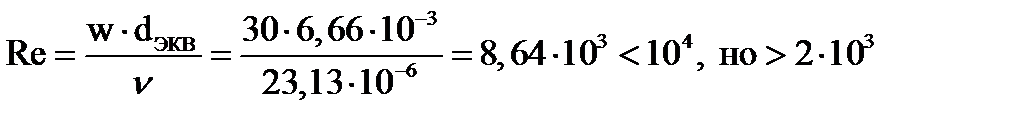
Режим течения – переходной. Критериальное уравнение для этого режима движения воздуха имеет вид:
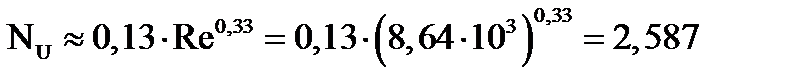
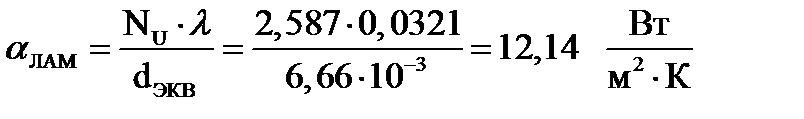
Для турбулентного режима:
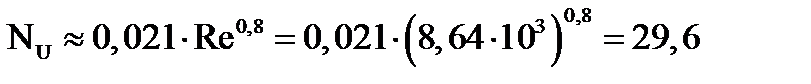
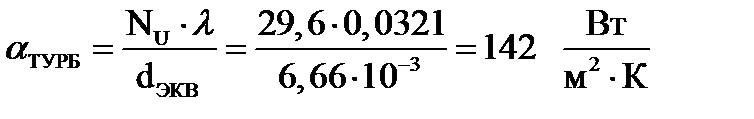
В этом случае α может меняться в диапазоне αперех = 12,14…142 [Вт/м2·К]
Задача 60.Определить плотность теплового потока, излучаемого абсолютно черным телом, если температура его: t = 1000 ºС, t = 0 ºС, t = – 20 ºС.
Решение:
В соответствии с законом Стефана-Больцмана:
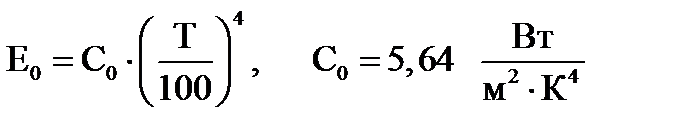
Для t = 1000 ºС:
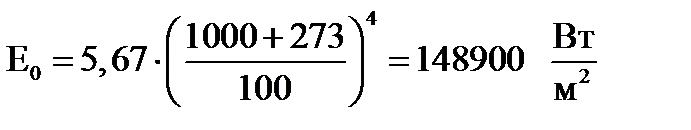
Для t = 0ºС:
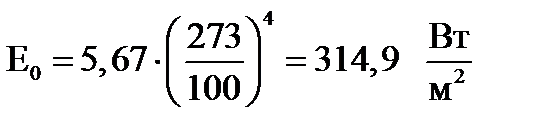
Для t = – 20ºС:
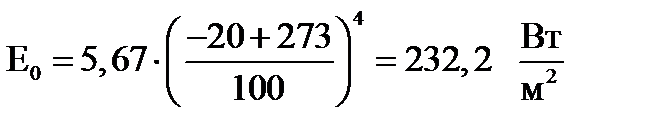
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|