
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Сложные электрические цепи постоянного тока
Внимательно изучить материал. Вспомнить второй Закон Кирхгофа. Следующие занятия на расчет цепи постоянного тока.
Тема: Сложные электрические цепи постоянного тока
Общие сведения
Электрические цепи с последовательно-параллельным соединением приемников энергии при питании их от одного источника электрической энергии, а также одноконтурные цепи называют простыми цепями. Расчет этих цепей осуществляется по формулам закона Ома и первого закона Кирхгофа. При этом заданные сопротивления часто заменяют одним эквивалентным. Так, цепь на рис. 6.1, а можно привести к элементарному виду с одним эквивалентным сопротивлением г, подключенным к источнику энергии с ЭДС Е1 (рис. 6.1,6). В данном случае 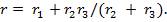 Электрические цепи с несколькими контурами, состоящими из разных ветвей с произвольным размещением потребителей и источников энергии, называются сложными электрическими цепями. Сложные электрические цепи рассчитывают методами: 1) узловых и контурных уравнений; 2) контурных токов; 3) узлового напряжения; 4) наложения (суперпозиции); 5) эквивалентного преобразования треугольника и звезды сопротивлений. В первом методе используются первый и второй законы Кирхгофа. Первый закон был рассмотрен в § 4.3.
Электрические цепи с несколькими контурами, состоящими из разных ветвей с произвольным размещением потребителей и источников энергии, называются сложными электрическими цепями. Сложные электрические цепи рассчитывают методами: 1) узловых и контурных уравнений; 2) контурных токов; 3) узлового напряжения; 4) наложения (суперпозиции); 5) эквивалентного преобразования треугольника и звезды сопротивлений. В первом методе используются первый и второй законы Кирхгофа. Первый закон был рассмотрен в § 4.3.
Второй закон Кирхгофа
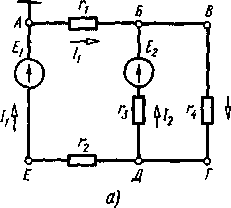
Сложная электрическая цепь(рис. 6.2, а) имеет два узла (Б и Д) и три ветви с токами 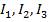 .Обозначим контуры цепи I — АБДЕА; II — АБВГДЕА; III — БВГДБ. В контуре АБДЕА включены ЭДС Е1, Е1 и сопротивления
.Обозначим контуры цепи I — АБДЕА; II — АБВГДЕА; III — БВГДБ. В контуре АБДЕА включены ЭДС Е1, Е1 и сопротивления 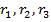 на которых создаются падения напряжения:
на которых создаются падения напряжения: 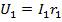 ,
, 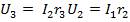 .
.
Если точку А заземлить, то ее потенциал будет равен нулю. Потенциалы точек Б и Д выразятся следующим образом: 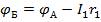 ;
; 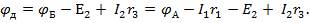
Если от потенциала 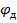 отнять падение напряжения
отнять падение напряжения 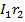 и прибавить к нему ЭДС Е1, то получим потенциал
и прибавить к нему ЭДС Е1, то получим потенциал 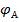 :
: 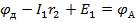 , или
, или 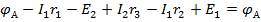 В левой части полученного равенства оставим ЭДС Е1 и Е2, а все остальные его члены перенесем в правую часть. Тогда получим
В левой части полученного равенства оставим ЭДС Е1 и Е2, а все остальные его члены перенесем в правую часть. Тогда получим 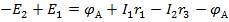 или
или 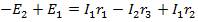
В левой части этого уравнения записана алгебраическая сумма ЭДС, действующих в первом контуре, а в правой — сумма падений напряжения во всех сопротивлениях, входящих в этот контур. В общем виде для любого контура
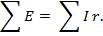
Равенство (6.1) является математическим выражением второго закона Кирхгофа: в любом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений в отдельных сопротивлениях.
Для каждого контура сложной электрической цепи по второму закону Кирхгофа можно составить только одно уравнение. При этом особое внимание следует обратить на знаки ЭДС и падение напряжения. Вначале произвольно выбирают направление обхода контура. Если действующая в контуре ЭДС совпадает с направлением обхода, то ее считают положительной, при обратном направлении ЭДС отрицательна. Падение напряжения на сопротивлении считают положительным, если направление тока в нем совпадает с направлением обхода контура
В электрических цепях встречаются элементы с выводами, на которых имеются напряжения U (сеть напряжения, делитель напряжения и т. д.). В этом случае удобнее использовать следующую форму записи второго закона Кирхгофа: 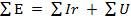 .
.
При этом ЭДС напряжения и токи, положительные направления которых совпадают с направлением обхода контура, записываются в соответствующую часть уравнения с положительным знаком.
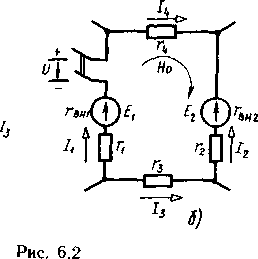
В противном случае эти же величины записываются с отрицательным знаком. Например, для контура (рис. 6.2, б) при обходе его по часовой стрелке имеем
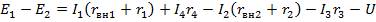
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|