Определенный интеграл. Определенный интеграл от функции f(x) на отрезе от а до b равен разности первообразных взятых от верхнего и нижнего пределов интегрирования.. Вычисление площадей плоских фигур с помощью определенного интеграла

Лекция

Определенный интеграл

1. Определение: Если предел интегральных сумм, при достаточном малом разбиении отрезков, стремится к одному и тому же конечному пределу А, то число А называется определенным интегралом от функции f(x) на отрезке от а до b. .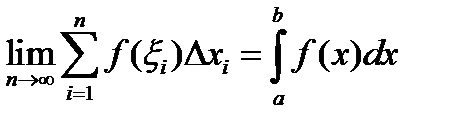

Формула Ньютона – Лейбница: .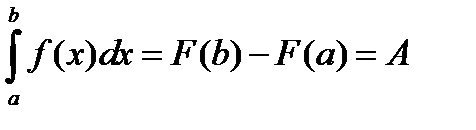

Определенный интеграл от функции f(x) на отрезе от а до b равен разности первообразных взятых от верхнего и нижнего пределов интегрирования.

2. Геометрический смысл определенного интеграла

Вычисление площадей плоских фигур с помощью определенного интеграла

а). Свойства площадей плоских фигур

Словесная формулировка	Математическая формулировка
Площадь величина положительная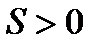
Равные площади имеют равные площади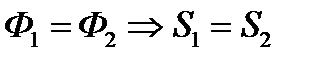
Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей ее частей
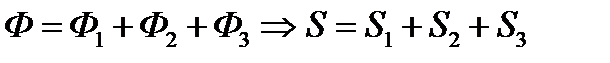
Площадь квадрата со стороной, равной единице измерения, равна единице.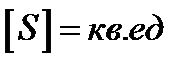

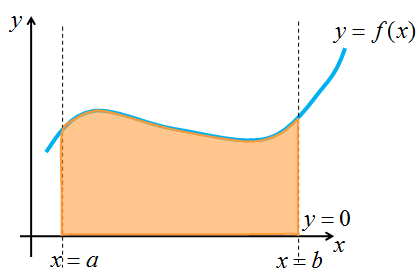
Варианты расположения плоских фигур

Дано	рисунок	формула

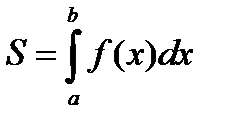
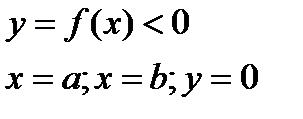
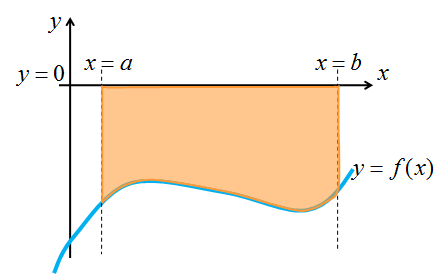
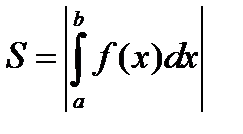
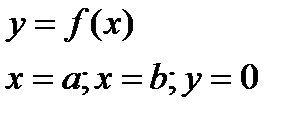
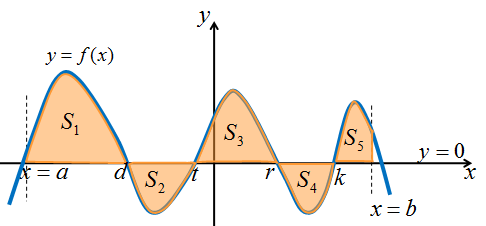
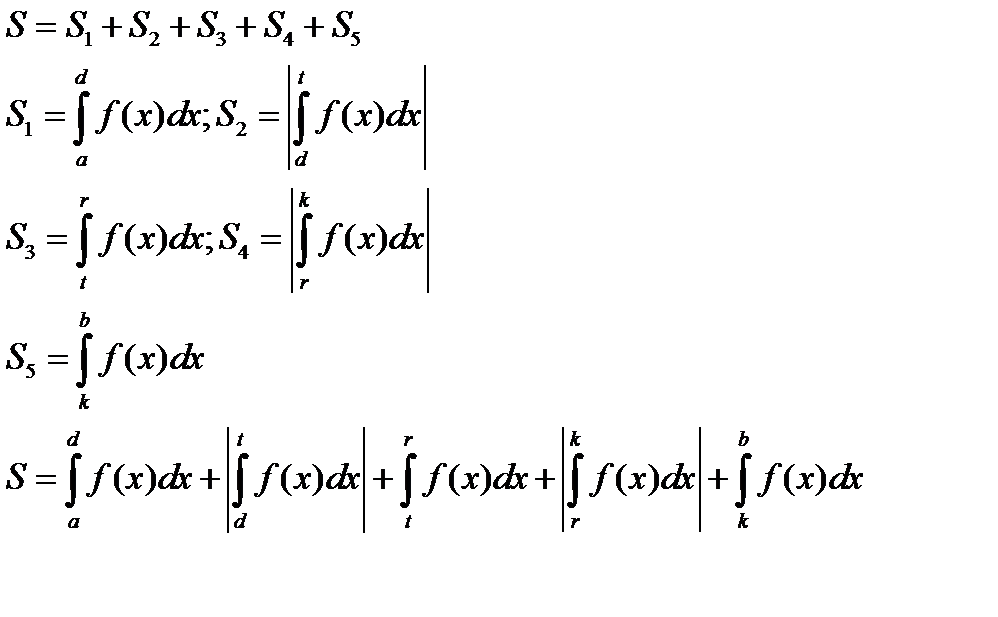
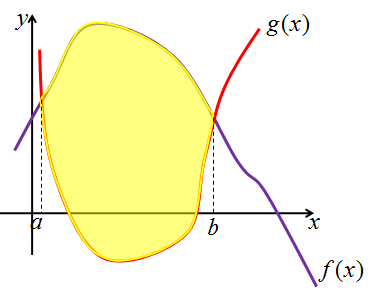
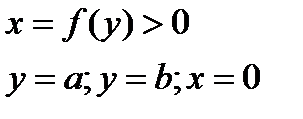
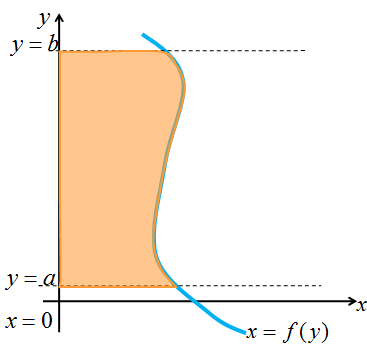
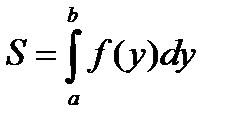
Пример: Найти площадь фигуры, ограниченной графиками функции .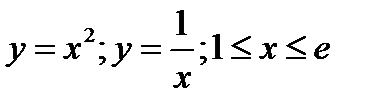

этапы	решение
1. По условию задачи делают схематический чертеж
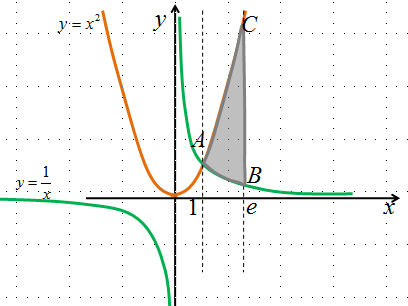
2. Определяем границы интегрирования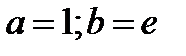
3. Вычисляем площадь криволинейного треугольника АВС

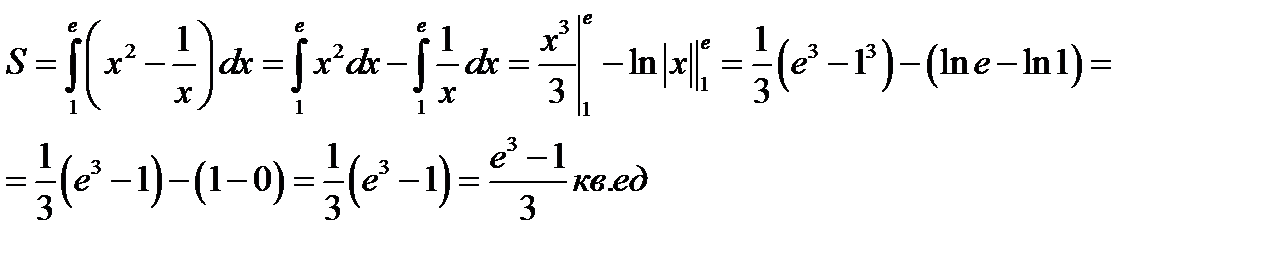
задача	формула
Вычисление объема тела по известным площадям его поперечных сечений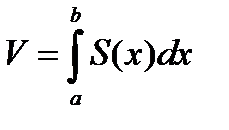
Вычисление объема тела вращения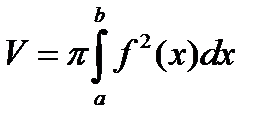
Длина дуг кривой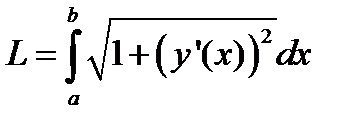
Площадь поверхности вращения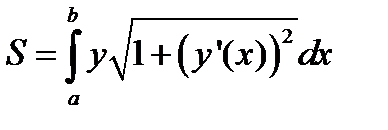

3. Применение определенного интеграла в физике.

задача	формула
Нахождение пути, пройденного телом при прямолинейном движении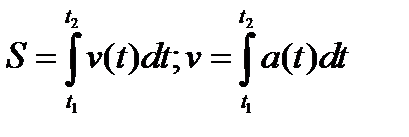
Вычисление работы силы, произведенной при прямолинейном движении тела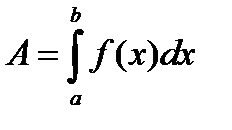
Вычисление работы, затраченной на растяжение или сжатие пружины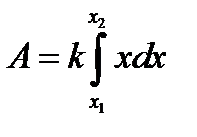
Определение силы давления жидкости на вертикально расположенную пластину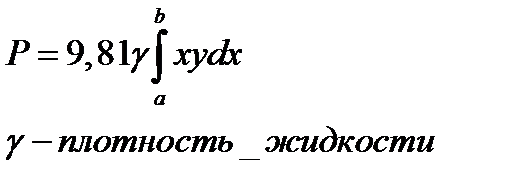
Вычисление массы стержня переменной плотности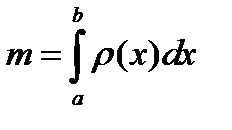
Вычисление электрического заряда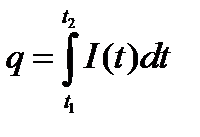
Вычисление теплоты, производимое телом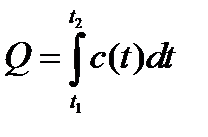
Работа газа при его расширении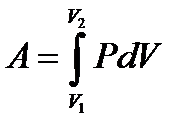

Пример: Два тела одновременно начали прямолинейное движение из некоторой точки в одном направлении со скоростям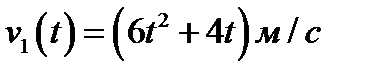и и 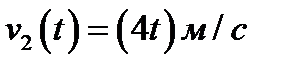. Через сколько секунд расстояние между ними будет равно 250м?

алгоритм	решение
1. Находим закон движения первого тела.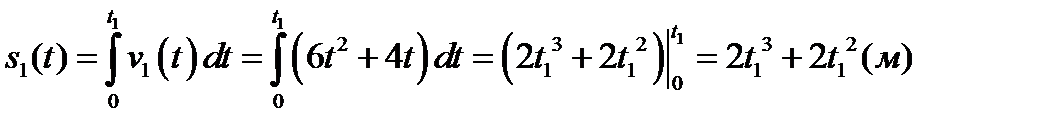
2. Находим закон движения второго тела.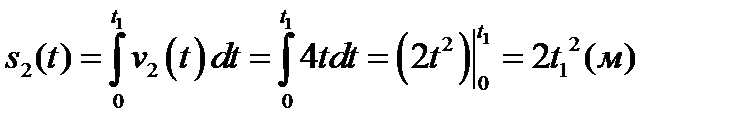
3.Так как расстояние между двумя телами 250 м, составляем уравнение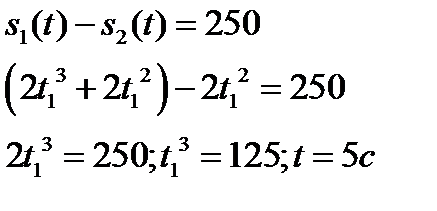
4. Записываем ответ

Пример: При растяжении пружины на 5см затрачивается работа 29,43Дж. На сколько растянется пружина, если затратить работу 9081 Дж?

алгоритм	решение
1. Определим коэффициент жесткости пружины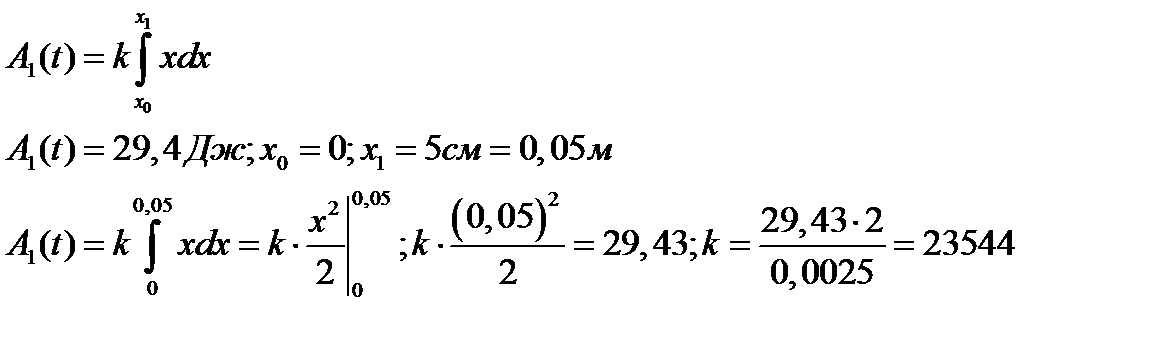
2. Находим на сколько можно растянуть пружину, затратив работу 9081 Дж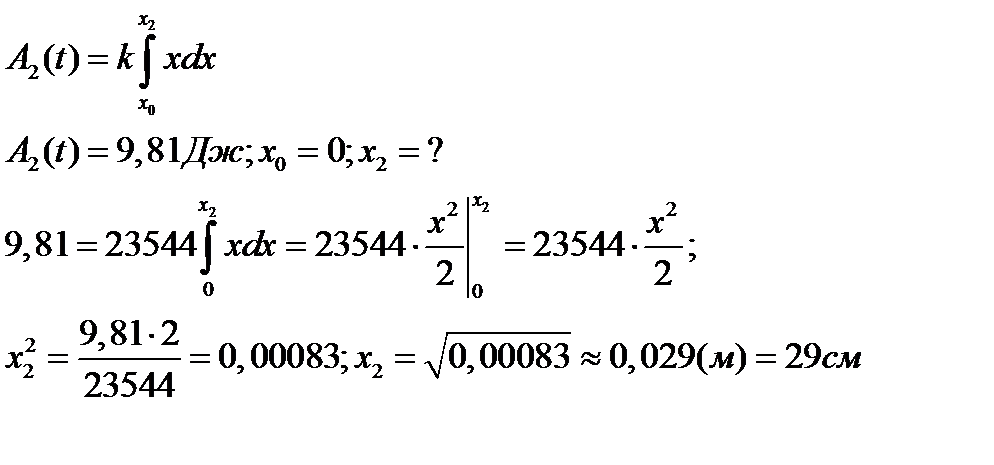
4. Записываем ответ