
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ВСЕРОССИЙСКАЯ ОЛИМПИАДА ШКОЛЬНИКОВ ПО МАТЕМАТИКЕ
ВСЕРОССИЙСКАЯ ОЛИМПИАДА ШКОЛЬНИКОВ ПО МАТЕМАТИКЕ
2017-2108 УЧЕБНЫЙ ГОД ВТОРОЙ ЭТАП
9 КЛАСС
РЕШЕНИЯ
1. Пусть 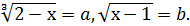 Тогда уравнение равносильно системе:
Тогда уравнение равносильно системе:
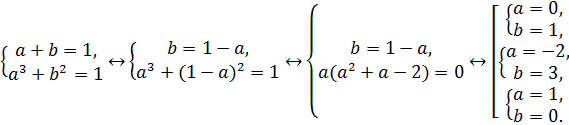
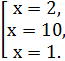
Ответ: 1, 2, 10.
2. Так как 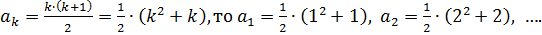 ,
, 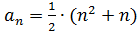 .
.
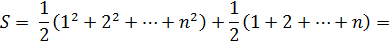
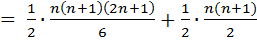 =
= 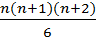 .
.
Подставим n=2017. Получим 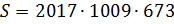 .
.
Ответ: 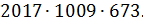
3. 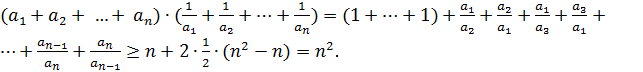
(t + 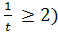


 4.
4.
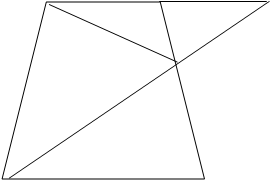 |



1. Продолжим ВС и АЕ до пересечения в точке К.
2. АВ = ВК (равнобедренный).
3. Δ СЕК подобен Δ ДЕА.
4. S(ΔBEC) = S(Δ СЕК)= ¼*S(ДЕА) = 2/
5. Δ ДЕА = Δ BЕА.
6. S(АВCД) = 8+8+2=18.
Ответ: 18.
5. Возьмём в качестве 1-ой группы городов любой город А. Во 2-ую группу включим все города, в которые можно сразу добраться из города А. В этих группах вместе не менее 101 города. В третью группу включим те города, в которые невозможно добраться непосредственно из города А, но можно добраться хотя бы из одного города второй группы. В четвёртую группу включим города, в которые невозможно непосредственно добраться ни из города А, ни из городов 2-ой группы, но можно добраться хотя бы из одного города третьей группы. В 3-ей, 4-ой и 5-ой группах не менее 101 города (в 4-ой группе есть хотя бы 1 город). И т.д. Предположим, что групп не менее 59 (т.е. пересадок 57 как минимум). В 6-ой, 7-ой, 8-ой группах городов не менее 101 и т.д. Таким образом всего городов в группах не менее 1*101+19*101=2020. По условию их 2017. Значит, групп не более 58, а пересадок не более 56. (Город А выбран произвольно)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|