Относительность механического движения.

Относительность механического движения.

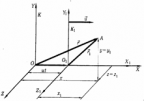
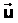1. Механическое движение можно наблюдать только относительно других тел. Обнаружить изменение положения тела, если не с чем сравнивать невозможно. 2. В различных системах отсчета физические величины (скорость, ускорение, перемещение и т.д.), характеризующие движение одного и того же тела, могут быть различными. 3. Характер движения, траектория движения и т.п. могут быть различны в разных системах отсчета для одного и того же тела могут быть различны.

Пусть две СО движутся друг относительно друга с постоянной скоростью

. Положение точки А в неподвижной системе К задано вектором

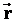, а в движущейся системе К₁ - вектором

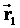. Из чертежа видим, что

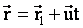. Это уравнение позволяет переходить из одной СО в другую. При этом мы считаем, что время течет в обеих СО одинаково. Будем условно называть системуК неподвижной, а систему К₁ - движущейся.

Тогда для случая, когда координаты y и z не меняются, получим: - преобразования Галилея.

Из этих уравнений следует: - расстояние между двумя точками абсолютно, т.е. не зависит от выбора СО. Пусть в неподвижной СО координаты точек x и x', а в подвижной соответственно x₁ и x₁'. Тогда

;

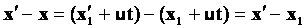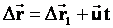Разделим правую и левую часть уравнения на промежуток времени, в течение которого шло перемещение. Получим: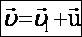

- закон сложения скоростей.Здесь скорость точки относительно неподвижной СО равна векторной сумме скорости точки относительно подвижной СО и скорости самой подвижной СО относительно неподвижной.

Скорость подвижной СО относительно неподвижной наз. переносной скоростью.

При решении задач часто бывает удобно принимать одно из движущихся относительно Земли тел за неподвижное. Тогда скорость Земли в этой СО будет равна по величине и противоположна по направлению скорости данного тела.

Если скоростиv₁ и u сонаправлены (тела сближаются), то их проекции складываются, если противоположно направлены (тела удаляются) – вычитаются. Если скорости направлены под прямым углом -

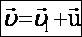
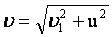, если угол произвольный, то необходимо пользоваться теоремой косинусов:

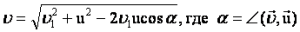Эти выводы справедливы для скоростей много меньших скорости света в вакууме (3^.10⁸м/с).

12 Следующая ⇒