
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
МЕХАНИКА ТВЕРДОГО ТЕЛА
6. МЕХАНИКА ТВЕРДОГО ТЕЛА
Динамика твердого тела
Уравнение движения центра масс твердого тела.
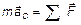
Ускорение центра масс 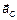 зависит от массы тела и от суммы (конечно векторной) всех сил, действующих на тело. Важно заметить, что ускорение центра масс тела не зависит от расположения точек приложения сил на теле.
зависит от массы тела и от суммы (конечно векторной) всех сил, действующих на тело. Важно заметить, что ускорение центра масс тела не зависит от расположения точек приложения сил на теле.
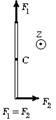 6.1 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы
6.1 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени: 1) угол a, который составляет со стержнем вектор
как показано на рис. Найдите для этого момента времени: 1) угол a, который составляет со стержнем вектор 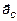 ускорения центра масс стержня; 2) модуль вектора
ускорения центра масс стержня; 2) модуль вектора 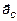 .
.
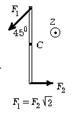
6.2 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени: 1) угол a, который составляет со стержнем вектор
как показано на рис. Найдите для этого момента времени: 1) угол a, который составляет со стержнем вектор 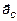 ускорения центра масс стержня; 2) модуль вектора
ускорения центра масс стержня; 2) модуль вектора 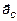 .
.
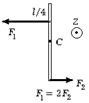 6.3 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы
6.3 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени: 1) угол a, который составляет со стержнем вектор
как показано на рис. Найдите для этого момента времени: 1) угол a, который составляет со стержнем вектор  ускорения центра масс стержня; 2) модуль вектора
ускорения центра масс стержня; 2) модуль вектора  .
.
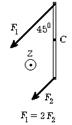 6.4 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы
6.4 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени: 1) угол a, который составляет со стержнем вектор
как показано на рис. Найдите для этого момента времени: 1) угол a, который составляет со стержнем вектор 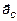 ускорения центра масс стержня; 2) модуль вектора
ускорения центра масс стержня; 2) модуль вектора 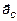 .
.
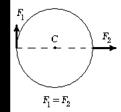
6.5 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени: 1) угол a, который составляет с вектором
как показано на рис. Найдите для этого момента времени: 1) угол a, который составляет с вектором  вектор
вектор 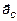 ускорения центра масс диска; 2) модуль вектора
ускорения центра масс диска; 2) модуль вектора 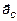 .
.
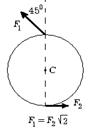 6.6 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы
6.6 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени: 1) угол a, который составляет с вектором
как показано на рис. Найдите для этого момента времени: 1) угол a, который составляет с вектором  вектор
вектор 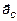 ускорения центра масс диска; 2) модуль вектора
ускорения центра масс диска; 2) модуль вектора 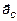 .
.
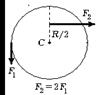 6.7 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы
6.7 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени: 1) угол a, который составляет с вектором
как показано на рис. Найдите для этого момента времени: 1) угол a, который составляет с вектором  вектор
вектор 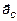 ускорения центра масс диска; 2) модуль вектора
ускорения центра масс диска; 2) модуль вектора 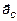 .
.
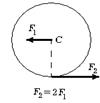 6.8 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы
6.8 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени: 1) угол a, который составляет с вектором
как показано на рис. Найдите для этого момента времени: 1) угол a, который составляет с вектором  вектор
вектор 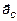 ускорения центра масс диска; 2) модуль вектора
ускорения центра масс диска; 2) модуль вектора 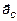 .
.
6.9 На гладкой горизонтальной плоскости находится однородный стержень длинной 2 м и массой 1 кг. К стержню, в точке, удаленной от его центра масс на расстояние 0,5 м, приложена горизонтальная сила величиной 10 Н, составляющая со стержнем угол 300. Вычислите для этого момента величину линейного ускорения центра масс стержня.
6.10 На гладкой горизонтальной плоскости находится однородный стержень длинной 2 м и массой 1 кг. К стержню, в его центре масс, приложена горизонтальная сила величиной 10 Н. Вычислите для этого момента величину линейного ускорения центра масс стержня.
6.11 На гладкой горизонтальной плоскости находится однородный стержень длинной 2 м и массой 1 кг. К каждому концу стержня, приложена горизонтальная сила величиной 10 Н, перпендикулярная стержню, причем направления сил противоположны. Вычислите для этого момента величину линейного ускорения центра масс стержня.
Момент сил, действующих на твердое тело.
 6.12 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы
6.12 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
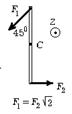 6.13 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы
6.13 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
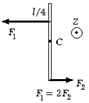 6.14 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы
6.14 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
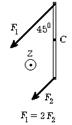 6.15 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы
6.15 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
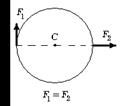 6.16 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы
6.16 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
 6.17 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы
6.17 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
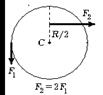 6.18 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы
6.18 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
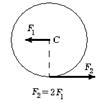 6.19 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы
6.19 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
как показано на рис. Найдите для этого момента времени величину и направление вектора момента сил, вычисленного относительно точки C.
Момент инерции твердого тела относительно постоянной оси вращения.
Определение.
Момент инерции материальной точки относительно оси вращения определяется как величина, равная произведению массы материальной точки на квадрат расстояния от этой точки до оси вращения:
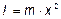 .
.
Момент инерции твердого тела относительно оси вращения – мера инертности твердого тела во вращательном движении (аналог массы в поступательном движении), определяется как величина, равная сумме моментов инерции достаточно малых фрагментов твердого тела. Достаточно малым фрагментом твердого тела является фрагмент, размеры которого малы по сравнению с расстоянием от фрагмента до оси вращения. Таким образом, этот фрагмент может быть назван материальной точкой и его момент инерции подсчитывается по формуле:
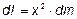 ,
,
а момент инерции всего твердого тела относительно постоянной оси вращения, по формуле:
 .
.
Для вычисления интеграла необходимо свести подинтегральное выражение к одной переменной величине. Это достигается, в частности, учетом как характера распределения массы тела по его объему, так и симметрии формы тела.
6.20 Найдите момент инерции тонкого кольца относительно оси, перпендикулярной плоскости кольца и проходящей через его центр. Масса кольца m, радиус кольца R.
6.21 Найдите момент инерции тонкостенного цилиндра относительно его оси симметрии, равноудаленной от всех точек цилиндра. Масса цилиндра m, радиус цилиндра R.
6.22 Найдите момент инерции однородного диска относительно его оси симметрии, перпендикулярной плоскости диска и проходящей через его центр. Масса диска m, радиус диска R.
6.23 Найдите момент инерции однородного сплошного цилиндра относительно его оси симметрии, равноудаленной от всех точек боковой поверхности цилиндра. Масса цилиндра m, радиус цилиндра R.
6.24 Найдите момент инерции однородного сплошного конуса относительно его оси симметрии, проходящей через вершину и центр основания конуса. Масса конуса m, радиус основания конуса R.
6.25 Найдите момент инерции тонкого однородного стержня относительно оси, перпендикулярной стержню и проходящей через его конец. Масса стержня m, его длина l.
6.26 Найдите момент инерции тонкого однородного стержня относительно оси, перпендикулярной стержню и проходящей через его середину. Масса стержня m, его длина l.
6.27 Найдите момент инерции тонкого однородного стержня относительно оси, перпендикулярной стержню и проходящей через точку стержня, которая делит его длину в отношении один к трем. Масса стержня m, его длина l.
6.28 Найдите момент инерции тонкого однородного стержня относительно оси, перпендикулярной стержню и проходящей через точку стержня, которая делит его длину в отношении один к двум. Масса стержня m, его длина l.
6.29 Найдите момент инерции тонкой однородной пластинки имеющей форму равнобедренного прямоугольного треугольника относительно оси, совпадающей с одним из его катетов. Длина каждого катета a. Масса пластинки m.
6.30 Найдите момент инерции тонкой однородной пластинки имеющей форму равнобедренного прямоугольного треугольника относительно оси, совпадающей с его (треугольника) гипотенузой. Длина гипотенузы a. Масса пластинки m.
Момент инерции твердого тела относительно постоянной оси вращения.
Теорема о параллельных осях (теорема Штейнера).
Теорема связывает момент инерции 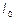 относительно произвольной оси с моментом инерции
относительно произвольной оси с моментом инерции 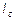 относительно параллельной ей оси, проходящей через центр масс твердого тела:
относительно параллельной ей оси, проходящей через центр масс твердого тела:
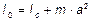 .
.
Здесь m - масса тела, a – расстояние между осями.
6.31 Найдите момент инерции тонкого кольца относительно оси, перпендикулярной плоскости кольца и проходящей через любую точку его окружности. Масса кольца m, радиус кольца R.
6.32 Найдите момент инерции однородного диска относительно оси, перпендикулярной плоскости диска и проходящей через его край. Масса диска m, радиус диска R.
6.33 Найдите момент инерции тонкого однородного стержня относительно оси, перпендикулярной стержню и проходящей через его конец, если известно, что момент инерции стержня относительно параллельной оси, проходящей через центр стержня, находится по формуле 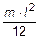 . Масса стержня m, его длина l.
. Масса стержня m, его длина l.
6.34 Найдите момент инерции тонкого однородного стержня относительно оси, перпендикулярной стержню и проходящей через точку стержня, которая делит его длину в отношении один к трем, если известно, что момент инерции стержня относительно параллельной оси, проходящей через центр стержня, находится по формуле 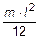 Масса стержня m, его длина l.
Масса стержня m, его длина l.
6.35 Найдите момент инерции тонкого однородного стержня относительно оси, перпендикулярной стержню и проходящей через точку стержня, которая делит его длину в отношении один к двум, если известно, что момент инерции стержня относительно параллельной оси, проходящей через центр стержня, находится по формуле 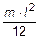 Масса стержня m, его длина l.
Масса стержня m, его длина l.
6.36 Найдите момент инерции тонкой однородной прямоугольной пластинки относительно оси, перпендикулярной ее плоскости и проходящей через одну из ее вершин, если известно, что момент инерции пластинки относительно параллельной оси, проходящей через ее центр, находится по формуле 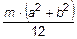 . Масса пластинки m, длины ее сторон a и b.
. Масса пластинки m, длины ее сторон a и b.
6.37 Найдите момент инерции тонкой однородной прямоугольной пластинки относительно оси, перпендикулярной ее плоскости и проходящей через середину стороны a, если известно, что момент инерции пластинки относительно параллельной оси, проходящей через ее центр, находится по формуле 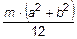 . Масса пластинки m, длины ее сторон a и b.
. Масса пластинки m, длины ее сторон a и b.
6.38 Найдите момент инерции тонкой однородной прямоугольной пластинки относительно оси, перпендикулярной ее плоскости и проходящей через одну из ее вершин. Масса пластинки m, длины ее сторон a и b.
6.39 Найдите момент инерции тонкой однородной прямоугольной пластинки относительно оси, перпендикулярной ее плоскости и проходящей через ее центр. Масса пластинки m, длины ее сторон a и b.
6.40 Найдите момент инерции тонкой однородной прямоугольной пластинки относительно оси, перпендикулярной ее плоскости и проходящей через середину стороны a. Масса пластинки m, длины ее сторон a и b.
6.41 Найдите момент инерции тонкой однородной пластинки имеющей форму равнобедренного прямоугольного треугольника относительно оси, перпендикулярной ее плоскости и проходящей через вершину прямого угла треугольника. Длина каждого катета a. Масса пластинки m.
Момент инерции твердого тела относительно постоянной оси вращения.
Теорема о взаимно перпендикулярных осях.
Момент инерции плоского тела относительно произвольной оси Z, перпендикулярной его плоскости, равен сумме моментов инерции относительно двух взаимно перпендикулярных осей X и Y, лежащих в плоскости тела и пересекающихся с осью Z:
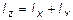 .
.
6.42 Момент инерции тонкого кольца относительно оси Z, перпендикулярной плоскости кольца и проходящей через его центр равен 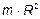 . Масса кольца m, радиус кольца R. Найдите момент инерции кольца
. Масса кольца m, радиус кольца R. Найдите момент инерции кольца 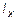 относительно оси X, совпадающей с диаметром кольца.
относительно оси X, совпадающей с диаметром кольца.
6.43 Момент инерции однородного диска относительно оси Z, перпендикулярной плоскости диска и проходящей через его центр равен 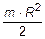 . Масса диска m, радиус диска R. Найдите момент инерции диска
. Масса диска m, радиус диска R. Найдите момент инерции диска 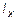 относительно оси X, совпадающей с диаметром диска.
относительно оси X, совпадающей с диаметром диска.
6.44 Момент инерции тонкой однородной прямоугольной пластинки относительно оси Z , перпендикулярной ее плоскости и проходящей через одну из ее вершин равен 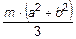 . Масса пластинки m, длины ее сторон a и b. Найдите момент инерции пластинки
. Масса пластинки m, длины ее сторон a и b. Найдите момент инерции пластинки 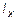 относительно оси X, совпадающей с ее стороной a .
относительно оси X, совпадающей с ее стороной a .
6.45 Момент инерции тонкой однородной прямоугольной пластинки относительно оси Z , перпендикулярной ее плоскости и проходящей через одну из ее вершин равен 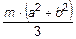 . Масса пластинки m, длины ее сторон a и b. Найдите момент инерции пластинки
. Масса пластинки m, длины ее сторон a и b. Найдите момент инерции пластинки 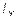 относительно оси Y, совпадающей с ее стороной b .
относительно оси Y, совпадающей с ее стороной b .
6.46 Момент инерции тонкой однородной прямоугольной пластинки относительно оси Z , перпендикулярной ее плоскости и проходящей через ее центр равен 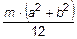 . Масса пластинки m, длины ее сторон a и b. Найдите момент инерции пластинки
. Масса пластинки m, длины ее сторон a и b. Найдите момент инерции пластинки 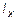 относительно оси X, параллельной стороне a и проходящей через центр пластинки.
относительно оси X, параллельной стороне a и проходящей через центр пластинки.
6.47 Момент инерции тонкой однородной прямоугольной пластинки относительно оси Z , перпендикулярной ее плоскости и проходящей через ее центр равен 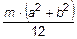 . Масса пластинки m, длины ее сторон a и b. Найдите момент инерции пластинки
. Масса пластинки m, длины ее сторон a и b. Найдите момент инерции пластинки 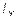 относительно оси Y, параллельной стороне b и проходящей через центр пластинки.
относительно оси Y, параллельной стороне b и проходящей через центр пластинки.
6.48 Момент инерции тонкой однородной пластинки, имеющей форму равнобедренного прямоугольного треугольника, относительно оси X, совпадающей с одним из его катетов равен 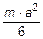 . Длина каждого катета a. Масса пластинки m. Найдите момент инерции пластинки
. Длина каждого катета a. Масса пластинки m. Найдите момент инерции пластинки 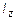 относительно оси Z, перпендикулярной плоскости пластинкии проходящей через вершину прямого угла треугольника.
относительно оси Z, перпендикулярной плоскости пластинкии проходящей через вершину прямого угла треугольника.
Уравнение вращательного движения твердого тела вокруг постоянной оси.
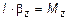
Уравнение записано в проекции на совмещенную с осью вращения координатную ось Z.
 6.49 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы
6.49 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора
как показано на рис. Найдите для этого момента времени величину и направление вектора 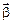 углового ускорения стержня.
углового ускорения стержня.
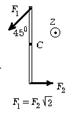 6.50 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы
6.50 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора
как показано на рис. Найдите для этого момента времени величину и направление вектора 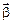 углового ускорения стержня.
углового ускорения стержня.
 6.51 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы
6.51 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора
как показано на рис. Найдите для этого момента времени величину и направление вектора 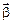 углового ускорения стержня.
углового ускорения стержня.
 6.52 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы
6.52 На гладкой горизонтальной поверхности стола покоится однородный стержень длины l и массы m. В некоторый момент времени к стержню прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора
как показано на рис. Найдите для этого момента времени величину и направление вектора 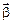 углового ускорения стержня.
углового ускорения стержня.
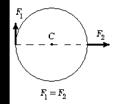
6.53 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора
как показано на рис. Найдите для этого момента времени величину и направление вектора 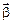 углового ускорения диска.
углового ускорения диска.
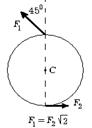 6.54 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы
6.54 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора
как показано на рис. Найдите для этого момента времени величину и направление вектора 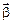 углового ускорения диска.
углового ускорения диска.
 6.55 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы
6.55 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора
как показано на рис. Найдите для этого момента времени величину и направление вектора 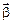 углового ускорения диска.
углового ускорения диска.
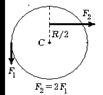
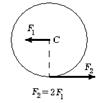 6.56 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы
6.56 На гладкой горизонтальной поверхности стола покоится однородный диск радиуса R и массы m. В некоторый момент времени к диску прикладывают горизонтальные силы  и
и  как показано на рис. Найдите для этого момента времени величину и направление вектора
как показано на рис. Найдите для этого момента времени величину и направление вектора 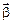 углового ускорения диска.
углового ускорения диска.
6.57 На гладкой горизонтальной плоскости находится однородный стержень длинной 2 м и массой 1 кг. К стержню, в точке, удаленной от его центра масс на расстояние 0,5 м, приложена горизонтальная сила величиной 10 Н, составляющая со стержнем угол 300. Вычислите, для этого момента. величину углового ускорения стержня.
6.58 На гладкой горизонтальной плоскости находится однородный стержень длинной 2 м и массой 1 кг. К стержню, в его центре масс, приложена горизонтальная сила, величиной 10 Н. Вычислите, для этого момента, величину углового ускорения стержня.
6.59 На гладкой горизонтальной плоскости находится однородный стержень длинной 2 м и массой 1 кг. К каждому концу стержня, приложена горизонтальная сила величиной 10 Н, перпендикулярная стержню, причем направления сил противоположны. Вычислите, для этого момента, величину углового ускорения стержня.
6.60 Диск массой 1 кг и радиусом 0,5 м вращается вокруг постоянной оси, проходящей через его центр. По касательной к ободу диска прикладывают постоянную тормозящую силу 10 Н. В результате диск, имевший начальную угловую скорость 400 1/с, останавливается через некоторое время. Вычислите это время.
6.61 Диск массой 1 кг и радиусом 0,5 м вращается вокруг постоянной оси, проходящей через его центр. По касательной к ободу диска прикладывают некоторую постоянную тормозящую силу. В результате диск, имевший начальную угловую скорость 400 1/с, останавливается через 1 с. Вычислите величину тормозящей силы.
6.62 Однородный диск массой 50 кг и радиусом 0,4 м вращается вокруг постоянной оси, перпендикулярной плоскости диска и проходящей через его центр, с частотой 8 с-1. К диску приложили постоянный момент сил трения, и через 60 с диск остановился. Вычислите величину момента сил трения.
6.63 К легкому диску радиусом 0,2 м приклеили тяжелое тонкое кольцо такого же радиуса так, что центры диска и кольца совпдают. В результате получился маховик, масса которого 5 кг однородно распределена по его ободу. Маховик вращается с частотой 10 с-1. К маховику приложили постоянный момент сил трения, и через 20 с он остановился. Вычислите величину момента сил трения.
6.64 Однородный диск массой 10 кг и радиусом 0,1 м вращается вокруг постоянной оси, перпендикулярной плоскости диска и проходящей через его центр, с угловой скоростью 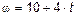 . Вычислите величину касательной силы, приложенной к ободу диска.
. Вычислите величину касательной силы, приложенной к ободу диска.
6.65 К легкому диску приклеили тяжелое тонкое кольцо такого же радиуса так, что центры диска и кольца совпдают. В результате получился маховик, масса которого 20 кг однородно распределена по его ободу. Радиус маховика 0,2 м. Маховик вращается вокруг постоянной оси, перпендикулярной плоскости диска и проходящей через его центр, с угловой скоростью 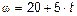 . Вычислите величину касательной силы, приложенной к ободу диска.
. Вычислите величину касательной силы, приложенной к ободу диска.
6.66 Однородный диск радиусом 0,1 м и массой 1 кг может вращаться практически без трения вокруг горизонтальной постоянной оси, проходящей через его центр. На обод диска намотана легкая нерастяжимая нить, к которой прикреплен груз массой 0,5 кг. Вычислите величину угловой скорости диска для момента времени, который наступит через 5 с после начала движения.
6.67 Однородный диск радиусом 0,1 м может вращаться практически без трения вокруг горизонтальной постоянной оси, проходящей через его центр. На обод диска намотана легкая нерастяжимая нить, к которой прикреплен груз массой 0,5 кг. Под действием силы тяжести и силы натяжения нити груз опускается на 1 м за 5 с. Вычислите момент инерции диска.
6.68 Однородный диск массой 1 кг может вращаться практически без трения вокруг горизонтальной постоянной оси, проходящей через его центр. По ободу диска сделан желоб, в который уложена легкая нерастяжимая нить. К концам нити прикреплены грузы массами 2 кг и 3 кг. Полагая, что нить по желобу не скользит, вычислите величину ускорения каждого из грузов.
6.69 Однородный диск радиусом 0,1 м может вращаться практически без трения вокруг горизонтальной постоянной оси, проходящей через его центр. По ободу диска сделан желоб, в который уложена легкая нерастяжимая нить. К концам нити прикреплены грузы массами 2 кг и 3 кг. Полагая, что нить по желобу не скользит, вычислите момент инерции блока относительно оси вращения, если величина углового ускорения блока равна 0,2 рад/с2.
6.70 На горизонтальной поверхности стола находится брусок массой m1, к которому прикреплена легкая нерастяжимая нить. Нить перекинута через блок (однородный диск) массой m, укрепленный на краю стола. На другом конце нити подвешен груз массой m2 . Коэффициент трения бруска по столу равен μ. Полагая, что блок вращается без трения и нить по блоку не скользит, найдите величину a1 ускорения бруска.
6.71 На горизонтальной поверхности стола находится брусок массой m1, к которому прикреплена легкая нерастяжимая нить. Нить перекинута через блок (однородный диск) массой m, укрепленный на краю стола. На другом конце нити подвешен груз массой m2 . Коэффициент трения бруска по столу равен μ. Полагая, что блок вращается без трения и нить по блоку не скользит, найдите величину a2 ускорения груза.
6.72 На горизонтальной поверхности стола находится брусок массой m1, к которому прикреплена легкая нерастяжимая нить. Нить перекинута через блок (однородный диск) радиусом R и массой m, укрепленный на краю стола. На другом конце нити подвешен груз массой m2 . Коэффициент трения бруска по столу равен μ. Полагая, что блок вращается без трения и нить по блоку не скользит, найдите величину β углового ускорения блока.
6.73 По наклонной плоскости, образующей с горизонтальной плоскостью угол α, скатывается без проскальзывания сплошной однородный цилиндр, причем образующая цилиндра горизонтальна. Найдите величиину линейного ускорения ac центра масс цилиндра.
6.74 По наклонной плоскости, образующей с горизонтальной плоскостью угол α, скатывается без проскальзывания однородная тонкостенная труба, причем образующая трубы горизонтальна. Найдите величину линейного ускорения ac центра масс трубы.
6.75 По наклонной плоскости, образующей с горизонтальной плоскостью угол α, скатывается без проскальзывания сплошной однородный цилиндр радиусом R , причем образующая цилиндра горизонтальна. Найдите величину углового ускоренияβ цилиндра.
6.76 По наклонной плоскости, образующей с горизонтальной плоскостью угол α, скатывается без проскальзывания однородная тонкостенная труба радиусом R, причем образующая трубы горизонтальна. Найдите величину углового ускоренияβ трубы.
Ответы
6.1. 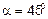 ;
; 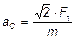
6.2. 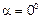 ;
; 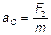
6.3. 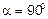 ;
; 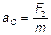
6.4. 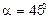 ;
; 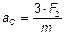
6.5. 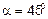 ;
; 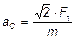
6.6.  ;
; 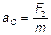
6.7. 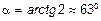 ;
; 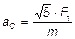
6.8. 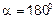 ;
; 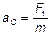
6.9. 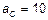 м/с2
м/с2
6.10. 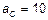 м/с2
м/с2
6.11. 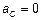
6.12. 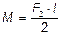 ; Вектор
; Вектор 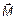 направлен к читателю вдоль оси Z
направлен к читателю вдоль оси Z
6.13. 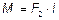 ; Вектор
; Вектор 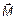 направлен к читателю вдоль оси Z
направлен к читателю вдоль оси Z
6.14. 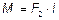 ; Вектор
; Вектор 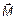 направлен к читателю вдоль оси Z
направлен к читателю вдоль оси Z
6.15. 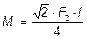 ; Вектор
; Вектор 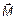 направлен к читателю вдоль оси Z
направлен к читателю вдоль оси Z
6.16. 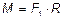 ; Вектор
; Вектор 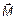 направлен от читателя
направлен от читателя
6.17. 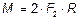 ; Вектор
; Вектор 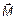 направлен к читателю
направлен к читателю
6.18. 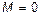
6.19. 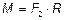 ; Вектор
; Вектор 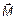 направлен к читателю
направлен к читателю
6.20. 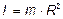
6.21. 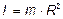
6.22. 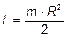
6.23. 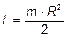
6.24. 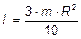
6.25. 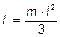
6.26. 
6.27. 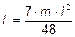
6.28. 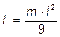
6.29. 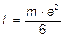
6.30. 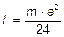
6.31. 
6.32. 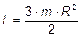
6.33. 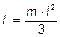
6.34. 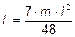
6.35. 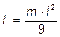
6.36. 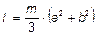
6.37. 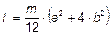
6.38. 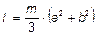
6.39. 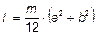
6.40. 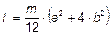
6.41. 
6.42.