
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Функция двух переменных. Ее область определения, предел, непрерывность.
1 Функция двух переменных. Ее область определения, предел, непрерывность.





2. Частные производные первого порядка и их геометрический смысл



3 Дифференцируемость функции двух переменных, дифференциалы. Геометрический смысл полного дифференциала.


4 Применение полного дифференциала к приближенным вычислениям.

5 Производная сложной функции.


6 Дифференцирование неявно заданной функции.


7 Частные производные и дифференциалы высших порядков.

8 Касательная плоскость и нормаль к поверхности.



9 Формула Тейлора функции двух переменных.
10 Экстремум функции двух переменных. Необходимые и достаточные условия экстремума.



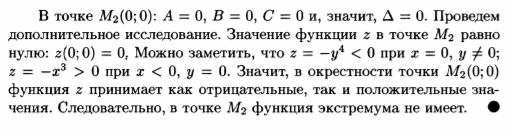
11. Скалярное поле. Производная по направлению. Градиент.


12. Двойной интеграл: определение, геометрический смысл. Достаточное условие интегрируемости функции.



13 Основные свойства двойного интеграла. 

14 Вычисление двойного интеграла в декартовых координатах.




15 Вычисление двойного интеграла в криволинейных координатах. Случай полярных координат.



16 Геометрические приложения двойного интеграла.



17. Криволинейные интегралы первого рода. Определение, теорема существования, свойства. 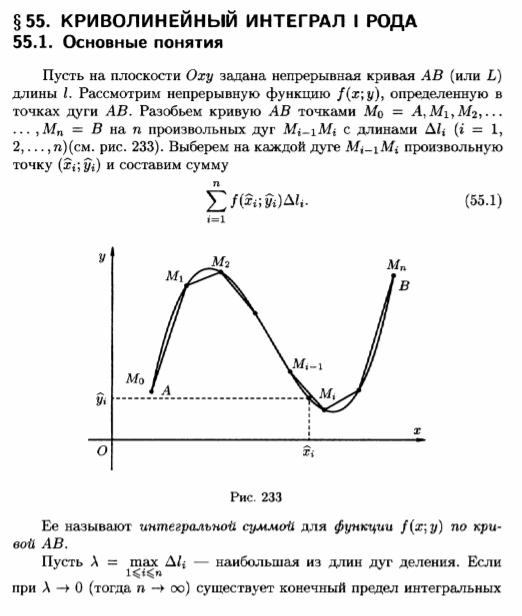


18 Вычисление криволинейного интеграла первого рода в различных случаях задания кривой интегрирования.

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|