Контакты

Случайная статья

Практическое занятие №72 «Нахождение наибольшего, наименьшего значения функции».

Стр 1 из 2Следующая ⇒

Практическое занятие №72 «Нахождение наибольшего, наименьшего значения функции».

Цель: выяснить в каких точках функция может достигать наибольшего и наименьшего значения, научиться определять наибольшее и наименьшее значение функции, заданной аналитическим способом, на отрезке.

Задание 1 (5 мин.).Ответить на вопросы:

А) Какие точки называют критическими?

Б) Какие точки на заданном графике являются критическими?

Задание 2 (5 мин.).Найти производную функции f(x) = -5х³+4х²-6х+7

Задание 3 (5 мин.).Найти значение функции y = 2x³+6x²-7x при х=2.

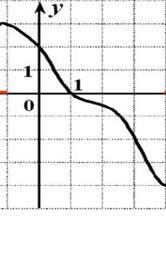
Задание 4 (5 мин.).Определить по графику наибольшее и наименьшее значение функции на заданном отрезке, и при каких значениях «х» они достигаются:

А) На отрезке [ 1;6 ] y_наиб.=… , при х =… , y_наим.=…., при х =…

Б) На отрезке [ -1;3,5 ] y_наиб.=…, при х=… ,

y_наим.=…,при х=…

3,5

-1

Задание 5 (5 мин.).Ответить на вопрос:

Как можно назвать значения «х» № 4 , в которых функция достигает наибольшего и наименьшего значения?

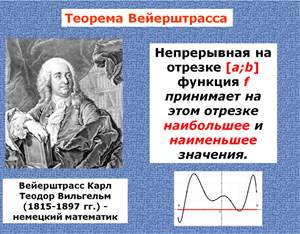
Задание 6 (5 мин.). Записать теорему.

Задание 7 (5 мин.). Записать алгоритм.

Задание 8 (10 мин.). Изучить Пример 1.

Пример 1 (к.р., экз.).Найти наибольшее и нпименьшее значение функции y =2х³-3х²-12х +1 на отрезке [1;3] .

Решение:

1. Найдем критические точки функции.

Y ^/ =(2х³-3х²-12х +1)^/ = (2х³)^/-(3х²)^/ – (12х)^/ +(1)^/= 2(х³)^/-3(х²)^/ – (12х)^/ +(1)^/=2∙3х² - 3∙2х – 12 + 0 = 6 х²- 6х – 12.

6 х²- 6х – 12 = 0

а=6, b=-6, c=-12

= (-6)²-4∙6∙(-12) = 36+288= 324

x _1,2 = = =

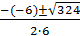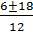
x ₁ = = 2 , x ₂ = = -1 – это критические точки.

Определим, какие точки попадают в интервал (1;3):

x ₁ = 2Î(1;3), x ₂= -1Ï(1;3).

2. Вычислим значение функции в критической точке x = 2и на концах отрезка, т.е. в точках х =1 и х=3:

У(2) =2∙2³-3∙2²-12∙2 +1= 16-12-24+1=

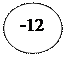У(1) =2∙1³-3∙1²-12∙1 +1= 2-3-12+1=

У(3) =2∙3³-3∙3²-12∙3 +1= 54-27-36+1=

3. Среди полученных значений выберем наибольшее и наименьшее:

y_наиб= - 8

y_наим.= -19

Ответ: y_наиб= - 8, y_наим.= -19

Задание 9 (10 мин.) (к.р., экз.). Найти наибольшее и нпименьшее значение функции y=4x²+16x-2 на отрезке [-1; 3].

Домашнее задание:

1. Выучить теорему , алгоритм, переписать Пример1.

2. Выполнить и сдать 07.06.20 до 18-00 самостоятельную работу.

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.