
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Инструкционная карта. практического занятия. курс ІІ группа_____, специальность 13.02.11 (ТЭО) 21.01.15(ОГР)
Инструкционная карта
практического занятия
курс ІІ группа_____________, специальность 13.02.11 (ТЭО) 21.01.15(ОГР)
Тема занятия: «Выполнение действий над комплексными числами в разных формах записей»
Цель занятия:
Дидактическая: отработать умения и навыки использования всех трёх форм комплексного числа при решении упражнений.
Воспитательная: показать роль личной ответственности студента за качество выполненной работы, роль систематичной работы студента в аудитории и дома; формирования умений и навыков для углубления и повышения качества знаний.Междисциплинарная интеграция: «Общая электротехника», «Общая электротехника с основами электроники».Методическое обеспечение:инструкционные карты, опорные конспекты по указанной теме.Теоретическое обоснование работы:Алгебраическая форма комплексного числа имеет вид: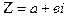 , где
, где 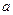 - действительная часть;
- действительная часть; 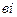 - мнимая часть комплексного числа.
- мнимая часть комплексного числа.Тригонометрическая форма комплексного числа:
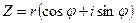 , где
, где 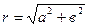 - модуль
- модуль 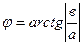 - аргумент комплексного числа. Формулы перехода от тригонометрической к алгебраической форме записи комплексных чисел:
- аргумент комплексного числа. Формулы перехода от тригонометрической к алгебраической форме записи комплексных чисел: 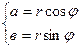 Показазательная форма комплексного числа имеет вид:
Показазательная форма комплексного числа имеет вид: 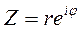 , где
, где 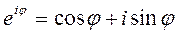 - формула Эйлера Примечание: Методика выполнения действий над комплексными числами в разных формах записи отображена в методической разработке «Комплексные числа».Ход работы 1. Выполнить действия над комплексными числами в заданной форме записи. Перейти к двум другим формам комплексных чисел (1 задание соответствующего варианта).2. Представить число
- формула Эйлера Примечание: Методика выполнения действий над комплексными числами в разных формах записи отображена в методической разработке «Комплексные числа».Ход работы 1. Выполнить действия над комплексными числами в заданной форме записи. Перейти к двум другим формам комплексных чисел (1 задание соответствующего варианта).2. Представить число 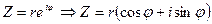 - тригонометрическая форма.
- тригонометрическая форма. 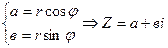 -алгебраическая форма комплексного числа.Примечание: При вычислении значений а и в следует использовать формулы приведения.1. При углах
-алгебраическая форма комплексного числа.Примечание: При вычислении значений а и в следует использовать формулы приведения.1. При углах 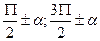 - название тригонометрической функции изменяется;
- название тригонометрической функции изменяется; 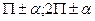 - остаётся неизменной.2. Знак в правой части ставится по знаку тригонометрической функции в начальной четверти. Варианты заданий: 1. а)
- остаётся неизменной.2. Знак в правой части ставится по знаку тригонометрической функции в начальной четверти. Варианты заданий: 1. а) 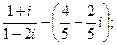
 б)
б) 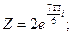
2. а) 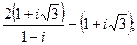 б)
б) 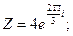
3. а)  б)
б) 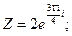
4. а) 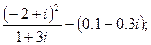
 б)
б) 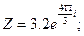
5. а) 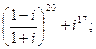 б)
б) 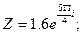
6. а) 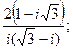 б)
б) 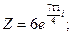
7. а) 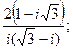 б)
б) 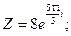
8. а) 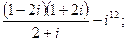 б)
б) 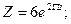
9. а) 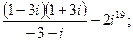 б)
б) 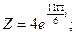
10. а) 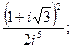 б)
б) 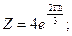
11. а) 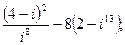 б)
б) 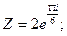
12. а) 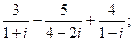 б)
б) 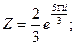
13. а) 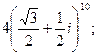 б)
б) 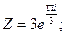
14. а) 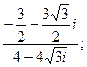 б)
б) 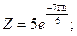
15. а) 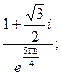 б)
б) 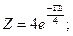
16. а)  б)
б) 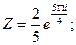
17. а) 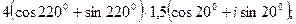 б)
б) 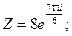
18. а) 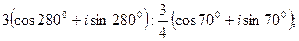 б)
б) 
19. а) 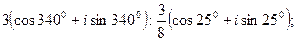 б)
б) 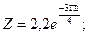
20. а) 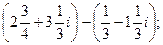 б)
б) 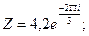
21. а) 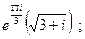 б)
б) 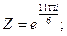
22. а) 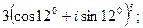 б)
б) 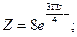
23. а) 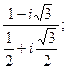 б)
б) 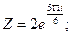
24. а) 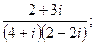 б)
б) 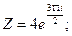
25. а) 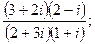 б)
б) 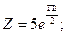
26. а) 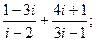 б)
б) 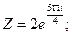
27. а) 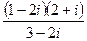 б)
б) 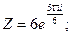
28. а) 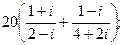 б)
б) 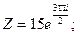
29. а) 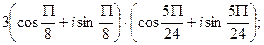 б)
б) 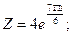
30. а) 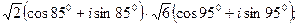 б)
б) 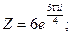
Вопросы для самопроверки:
1. Найдите действительные числа а и в так, чтобы выполнялись уравнения:
а) 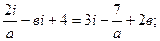
б) 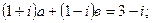
2. Вычислить:
а) 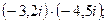
б) 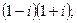
в) 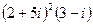
3. Решить квадратные уравнения :
а) 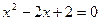
б) 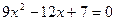
Использованная литература.
1. А.А. Дадаян., И.А. Новик, «Алгебра начала и анализа» М. «Высшая школа»,1980.
2. Н.В. Богомолов. «Практические занятия по математике» М. «Высшая школа», 1979.
3. Г.Н. Яковлев. «Алгебра начала и анализа» ч. ІІ М. «Высшая школа»
Преподаватель:_______________________________Л.А.Пузанко
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|