Хелпикс

Главная

Контакты

Случайная статья



Прямая и плоскость в пространстве.



Прямая и плоскость в пространстве.

1.Уравнения плоскости в пространстве.

Произвольный вектор 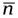ортогональный к плоскости 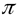(рис.1.1) называется 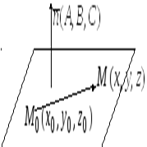еёнормальным вектором или нормалью к плоскости.

Рис.1.1

Пусть 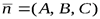, и 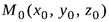заданная точка плоскости, тогда из условия ортогональности векторов 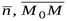(здесь и далее 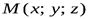произвольная точка плоскости), получим:

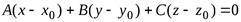(1.1)

- уравнение плоскости проходящей через данную точку в направлении данного вектора нормали.

Раскрывая скобки, и вводя новую константу 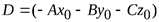, получим:

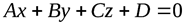(1.2)

– общее уравнение плоскости.

Преобразовав формулу (1.2) получим уравнение плоскости в отрезках: 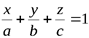(1.3)

где 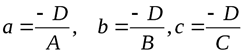- отрезки, отсекаемые плоскостью на координатных осях 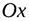, 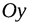и 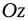соответственно (рис.1.2).

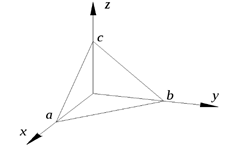
Рис.1.2

Три точки 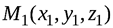, , 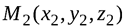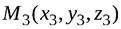лежат в одной плоскости (рис. 1.3) тогда и только тогда, когда векторы 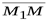, , 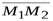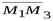компланарны: .

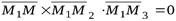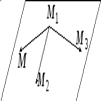Рис.1.3

 

 

Или в координатной форме:

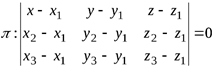(1.4)

уравнение плоскости проходящей через три точки.

Два неколлинеарных между собой вектора принадлежащих одной плоскости или параллельных ей, называются направляющими к этой плоскости.

Для того, чтобы записать уравнение плоскости, проходящей через заданную точку 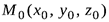и два направляющих вектора плоскости 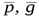, воспользуемся условием компланарности векторов 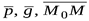(рис.1.4).

Рис.1.4

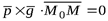или в координатной форме:

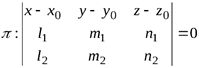(1.5)

  1. Уравнения прямой в пространстве

Прямую можно задавать либо двумя уравнениями плоскостей:

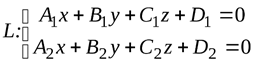(3.1)

Либо пучком плоскостей, проходящих через эту прямую:

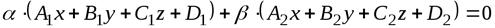(3.2)

Каждый ненулевой вектор будем называтьнаправляющим вектором этой прямой. Уравнение прямой, проходящей через заданную точку и имеющей заданный направляющий вектор 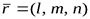получим из условия коллинеарности векторов 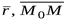(рис.3.1):

Рис.3.1

Векторы коллинеарны, следовательно их соответствующие координаты пропорциональны:

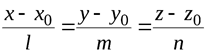(3.3)

Уравнение (3.3) принято называть каноническим уравнением прямой.

Уравнение прямой, проходящей через две заданные точк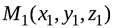и и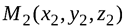можно записать используя тоже свойство коллинерности векторов 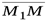и 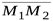(рис. 3.2)

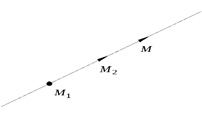
Рис.3.2

Получим уравнение прямой проходящей через две точки:

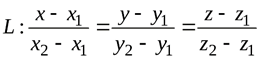(3.4)

Приравняем уравнение (3.3) произвольному параметру :

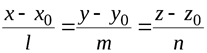
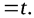
Получим систему равенств

, , ;

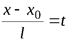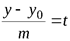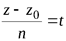определяющих параметрическое уравнение прямой:

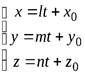(3.5)

2.Угол между прямой и плоскостью. Условие параллельности и ортогональности двух прямых, прямой и плоскости.

Рассмотрим пару прямых 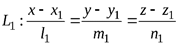и 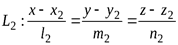. Расположение прямых в пространстве можно рассмотреть по расположению их направляющих векторов 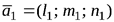и .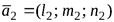

Если прямые параллельны, то координаты их направляющих векторов пропорциональны:

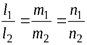(4.1)

Если прямые ортогональны, то скалярное произведение их направляющих векторов равно нулю:

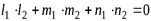(4.2)

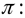
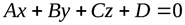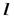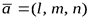
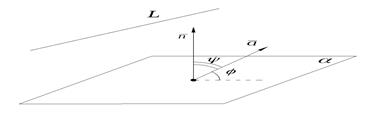Рассмотрим плоскость , и прямую имеющую направляющий вектор . Пустьφ – угол между прямой 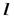и плоскостью 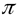(рис. 4.1).

Рис.4.1

Так как 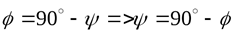, , 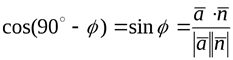тогда

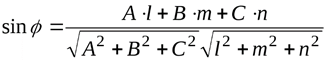(4.3)

Условие коллинеарности и ортогональности прямой и плоскости выводится из взаимного расположения их направляющих векторов:

1) если 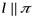, то 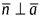и следовательно ,

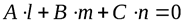(4.4)

2) если 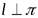, то 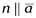и их координаты пропорциональны 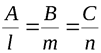(4.5)
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.