Вариант.. Вариант 2.. С рисунок 1.

Математика

6.02.2020г.

Гр. №12

Тема: Вычисление производных

1. Решить задания № 869 (1-5), 859(1-4)

2. Домашнее задание: № 822, № 857 (1-2)

Литература: Математика: алгебра и начала математического анализа, геометрия. Алимов Ш.А.

Гр. № 23

Тема: Контрольная работа

1 Вариант.

1.Выбери верный ответ:

I.Плоскость, притом только одна, проходит через …

а) любые три точки, не лежащие на одной прямой; б) любые три точки, лежащие на одной прямой;

в) любые три точки.

II.Плоскость, притом только одна, проходит через …

а) две пересекающиеся прямые;

б) две скрещивающиеся прямые; в) одну прямую.

III.Если две точки прямой принадлежат плоскости, то прямая …

а) лежит в плоскости;

б) пересекает плоскость;

в) параллельна плоскости.

2. Выбери все верные ответы:

I.Основными фигурами в стереометрии являются:

а) куб;

б) точка;

в) луч;

г) треугольник;

д) прямая;

е) плоскость.

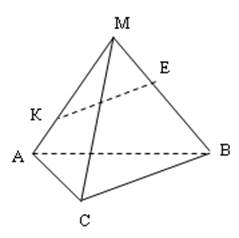
II. На рисунке 1 скрещивающимися являются прямые

(т.К принадлежит АМ, т.Е принадлежит МВ):

а) КЕ и ВС;

б) КЕ и АВ;

в) КЕ и МС;

г) КЕ и АС;

д) КЕ и АМ.

III. На рисунке 1 плоскости АМВ принадлежат точки

а) М;

б) А;

Рис. 1

в) К;

г) Е.

3.Если через две параллельные прямые проходят пересекающиеся плоскости, то линия их пересечения

а) параллельна каждой из двух прямых или совпадает с одной из них;

б) пересекается хотя бы с одной из этих прямых;

в) скрещивается хотя бы с одной из прямых.

4.Каким может быть взаимное расположение двух прямых, если обе они параллельны одной плоскости?

а) только параллельны;

б) все случаи взаимного расположения;

в) только скрещиваются;

г) только пересекаются.

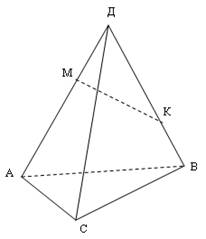
5. В тетраэдре ДАВС точка М лежит на ребре АД, а точка К на ребре ДВ (рис. 2). Точка пересечения прямой МК и плоскости АВС лежит на прямой…

а) ВС;

б) АВ;

в) АС;

г) ДС.

6. Основание AD трапеции ABCD лежит в плоскости α. Через точки B и C проведены параллельные прямые, пересекающие плоскость α в точках E и F соответственно.

а) Каково взаимное расположение прямых EF и АВ?

б) Чему равен угол между прямыми EF и АВ, если ?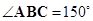

Ответ обоснуйте.

Вариант 2.

1.Выбери верный ответ:

Плоскость, притом только одна, проходит через

а) прямую;

б) прямую и не лежащую на ней точку,

в) прямую и лежащую на ней точку.

Плоскость, притом только одна, проходит через

а) две скрещивающиеся прямые;

б) две параллельные прямые;

в) прямую и лежащую на ней точку.

III. Если прямая и плоскость имеют только одну общую точку, топрямая

а) пересекает плоскость;

б) лежит в плоскости;

в) параллельна плоскости.

2. Выбери все верные ответы:

Основными фигурами в стереометрии являются:

а) куб;

б) точка;

в) луч;

г) треугольник;

д) прямая; К

е) плоскость.

А Р

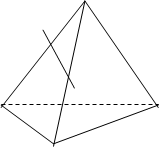
С рисунок 1.

I. На рисунке 1 скрещивающимися являются прямые

(т.М принадлежит АК, т.Р принадлежит КС):

а) АВ и МР; б) АС и МР; в) АВ и МР;

г) АК и МР; д) АС и КВ.

II. На рисунке 1 плоскости АКВ принадлежат точки

а) М; б) Р; в) В; г) С.

3. Выберите верное утверждение.

а) Две прямые называются параллельными, если они не имеют общих точек;

б) две прямые, параллельные третьей прямой, параллельны;

в) две прямые, перпендикулярные третьей прямой, параллельны;

г) если углы равны, то их стороны соответственно сонаправлены.

4. Каким может быть взаимное расположение прямых а и b, если прямая а лежит в плоскости α, а прямая b параллельна этой плоскости?

а) Параллельны или пересекаются; б) скрещиваются или пересекаются;

в) параллельны или скрещиваются; г) определить нельзя.

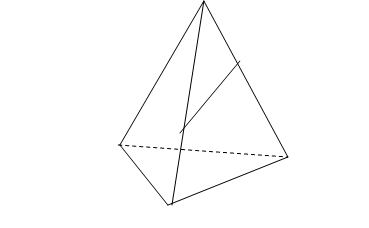
5.В тетраэдре МАВС точка О лежит на ребре МС, а точка К на ребре МВ

(рисунок 2). Точка пересечения прямой ОК и плоскости АВС лежит на прямой

а) АС; б) АВ; в) ВС; г) АМ.

А В

Рисунок 2.

6. Треугольники АВС и ADC лежат в разных плоскостях и имеют общую сторону AC. Точка

P - середина стороны AD, точка K – середина стороны DC.

а) Каково взаимное расположение прямых PK и AB?

б) Чему равен угол между прямыми PK и AB, если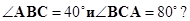

Ответ обоснуйте.

Контрольную работу оформить на 2 листочках в клетку. Номер варианта определить по нумерации фамилии в списке группы ( нечет- 1 вариант, чет- 2 вариант)

Гр. № 25.

Тема: Изображение пространственных фигур на плоскости.

1. Составить конспект по теме: «Изображение пространственных фигур на плоскости.» (стр. 220-224)

2. Домашнее задание: §4, п.12-13, № 71

Тема: Задачи на построение сечений

1. Составить конспект по теме: «Задачи на построение сечений» (§4, п.14, задачи 1-3)

2. Решить задачу № 72, № 79.

3. Домашнее задание:

Построить сечение многогранника плоскостью, проходящую через данные точки :

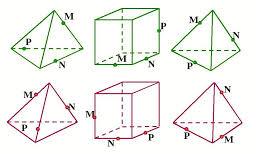
Литература: Учебник Геометрия 10-11, Атанасян Л. С.