Алгебраическая дробь. Основное свойство дроби, его применение.

Алгебраическая дробь. Основное свойство дроби, его применение.

Опр. 1. Выражения, составленные из чисел и переменных с помощью действий сложения, вычитания, умножения и деления на число отличное от нуля, называют целыми выражениями.

Примеры: 7a²b; m³+n³; (x-y)(x²+y²); b¹⁰- 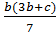; ; 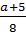2x; 9.

Опр. 2. Выражения, в которых кроме действий (сложение, вычитание, умножение, деление на число) есть деление на выражение с переменной, называют дробными выражениями.

Примеры: ; ;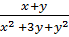

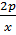Опр. 3. Целые и дробные выражения, называют рациональными выражениями.

Целые выражения в алгебре всегда имеют смысл, а дробные выражение при некоторых значениях переменных могут не иметь смысла.

Пример: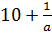

1) а=0, выражение не имеет смысл.

2) Выражение имеет смысл при всех а, кроме 0, или а≠0.

Опр. 4. Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных или областью допустимых значений (ОДЗ).

Примеры: 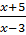, x – любое, кроме 3.

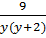, y – любое, кроме -2; 0.

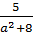, a – любое.

Частным случаем рационального выражения является рациональная дробь.

Примеры: ; ;

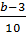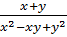
Опр. 5. Дробь, у которой числитель и знаменатель многочлен, называют рациональной дробью.

Основное свойство дроби, его применение.

Правило: Если числитель и знаменатель дроби умножить или разделить на одно и тоже число, то получится равное ей значение дроби.

;

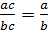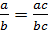
Эти равенства справедливы не только при натуральных a, b, c, но и при любых других значениях a, b, c, но b≠0, c≠0.

Опр: Тождеством называют равенство, верное при всех допустимых значениях входящих в него переменных.

Опр: Два выражения, принимая равные значения, при всех допустимых для них значениях входящих в них переменных называют, тождественно равными.

Опр: Замену одного выражения другим, тождественно равным, называют тождественным преобразованием выражения.

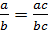умножение, тождество основное свойство дроби.

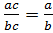деление, тождество основное свойство дроби.

Пример: 1) 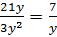; 2)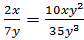

Если при сокращении дробей необходимо изменить знак, то его меняют дважды: 1) в числителе и знаменателе; 2) в числителе и перед дробью; 3) в знаменателе и перед дробью.

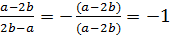
P.S. при сокращении противоположных выражений получается -1

P.S. нельзя сократить при сложении и вычитании (сокращают только множители).