ИЗУЧЕНИЕ РАСПРЕДЕЛЕНИЯ ГАУССА.

Лабораторная работа №1.

ИЗУЧЕНИЕ РАСПРЕДЕЛЕНИЯ ГАУССА.

ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ.

Цель работы: изучение экспериментального распределения значений непрерывной случайной величины. В качестве значений исследуемой величины используются значения, моделируемые генератором случайных чисел (данная модель представляет собой результаты измерений некоторой непрерывной случайной величины, выбранные случайным образом).

Ход работы:

1. Результаты измерений заносим в таблицу 1, которая составляет статистический ряд.

Таблица1.

i
X_i	6,75	6,56	8,48	7,45	6,51	4,69	6,29	6,85	6,22	8,65	5,40	7,77	9,93	8,10	6,29

i
X_i	4,42	7,05	5,61	6,77	8,17	8,24	4,28	6,28	4,82	5,31	7,40	9,89	7,43	5,83	5,15	9,00	10,22	3,59

i
X_i	3,47	7,70	9,57	6,10	8,32	8,74	5,33	9,63	4,80	3,78	4,19	8,76	5,81	7,80	8,48	8,41	7,23

i
X_i	10,76	5,02	8,13	9,10	3,67	7,40	7,33	10,96	6,42	7,96

2. Простой статистический ряд преобразуем в упорядоченный статистический ряд. Для этого в таблице 1 находим максимальное и минимальное значения и весь диапазон от x_min до x_max разбиваем на k (5) равных интервалов длинной ∆ Х.

X_max=10,96 ; X_min=3,47 ; K=5

∆X=(X_max-Xmin)/k

∆X= (10,96-3,47)/5=1,498

Затем вычисляем границы каждого из k интервалов по формуле X _j_,_max=X _j_,_min+j*∆X, где j=1,2..k

X _{1, max}=3,47+1*1,498=4,968

X _{2, max}=3,47+2*1,498=6,466

X _{3, max}=3,47+3*1,498=7,964

X _4,_max=3,47+4*1,498=9,462

X _5,_max=3,47+5*1,498=10,96

Нижние границы последующего интервала равны верхним границам предыдущего.

Находим число попавших в интервал значений m_j ,статистическую вероятность

и среднее арифметическое значение исследуемой величины Х для каждого интервала по формулам P_j=m_j/N и X̅= Σx_ij/m_j

m₁=10; P₁=10/60=0,17; X̅₁=4,171/10=0,417

m₂=14; P₂=14/60=0,23; X̅₂=5,79/14=0,414

m₃=16; P₃=16/60=0,27; X̅₃=7,248/16=0,453

m₄=13; P₄=13/60=0,22; X̅₄=8,506/13=0,654

m₅=7; P₅=7/60=0,12; X̅₅=10,137/7=1,448

Таблица2.

j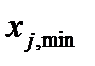
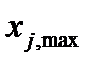
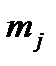
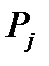
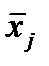
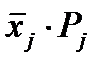
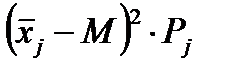
	3,47	4,968	0,17	4,219	0,717	0,0063
	4,968	6,466	0,23	5,717	1,315	0,0088
	6,466	7,964	0,27	7,215	1,948	0,0067
	7,964	9,462	0,22	8,713	1,917	0,0004
	9,462	10,96	0,121	10,21	1,235	0,0842

3. Вычисляем математическое ожидание исследуемой величины по формуле: M=Σx_j*P_j

просуммировав данные седьмого столбца таблицы 2.

M=0,717+1,315+1,948+1,917+1,235= 7,132

4. Вычисляем дисперсию и среднее квадратическое отклонение по формуле:

D=σ²=Σ(X̅_j-M)²*P_j

D₁=(4,219-7,132)²*0,17=1,4425

D₂=(5,717-7,132)²*0,23=0,4605

D₃=(7,215-7,132)²*0,27=0,0023

D₄=(8,713-7,132)²*0,22=0,55

D₅=(10,21-7,132)²*0,12=1,1369

D=1,4425+0,4605+0,0023+0,55+1,1369=3,592

σ =√D=1,8953

5. Вычисляем для каждого интервала параметры Z₁, Z₂ по формулам: Z₁= (a-M)/ σ и Z₂=(b-M)/ σ. При этом подставляем вместо a и b верхние и нижние границы интервала.

Z_1,1=(4,968-7,132)/ 1,8953=-1,14; Z_2,1=(3,47-7,132)/ 1,8953=- 1,93

Z_1,2=(6,466-7,132)/ 1,8953=- 0,35; Z_2,2=(4,968-7,132)/ 1,8953=- 1,14

Z_1,3=(7,964-7,132)/ 1,8953=0,44; Z_2,3=(6,466-7,132)/ 1,8953=- 0,35

Z_1,4=(9,462-7,132)/ 1,8953=1,23; Z_2,4=(7,964-7,132)/ 1,8953=0,44

Z_1,5=(10,96-7,132)/ 1,8953=2,02; Z_2,5=(9,462-7,132)/ 1,8953=1,23

Определяем значения функции Гаусса(нормальной функции распределения) для соответствующих

значений Z, находим теоретическую вероятность по формуле P_теор=Ф₂-Ф₁

12 Следующая ⇒