Численное решение обыкновенных дифференциальных уравнений.

Численное решение обыкновенных дифференциальных уравнений.

(вар.26)

1)Построить график и вывести в виде таблицы решение задачи Коши на интервале [0; 1] методом Рунге-Кутта 4-го порядка.

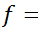
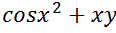
Для решения данной задачи воспользуемся функцией ode45.

1)Создаем m-файл

function dydx = fun(x,y);

dydx = [cos(x.^2)+x*y];

end

2)Создаём новый скрипт

tspan=[0 1];

x0=0.1;

[x,y] = ode45(@fun,tspan,x0);

plot(x,y)

grid on

title('Численное решение обыкновенных дифференциальных уравнений');

legend('f=cosx^2+xy')

Решение задачи Коши:

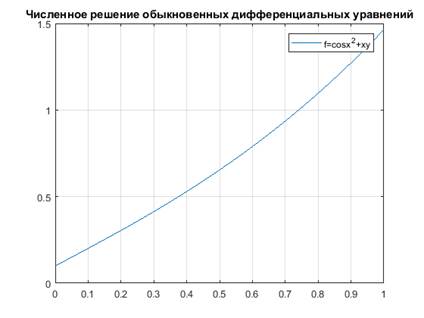
Таблица (численное решение):

X	Метод Рунге-Кутта	Точный метод
0.0050 0.0100 0.0151 0.0201 0.0451 0.0701 0.0951 0.1201 0.1451 0.1701 0.1951 0.2201 0.2451 0.2701 0.2951 0.3201 0.3451 0.3701 0.3951 0.4201 0.4451 0.4701 0.4951 0.5201 0.5451 0.5701 0.5951 0.6201 0.6451 0.6701 0.6951 0.7201 0.7451 0.7701 0.7951 0.8201 0.8451 0.8701 0.8951 0.9201 0.9401 0.9600 0.9800 1.0000	0.1000 0.1050 0.1101 0.1151 0.1201 0.1452 0.1705 0.1958 0.2214 0.2472 0.2732 0.2995 0.3261 0.3530 0.3803 0.4080 0.4362 0.4648 0.4938 0.5234 0.5536 0.5843 0.6156 0.6476 0.6802 0.7134 0.7474 0.7821 0.8176 0.8538 0.8909 0.9287 0.9674 1.0070 1.0475 1.0888 1.1311 1.1743 1.2185 1.2637 1.3099 1.3475 1.3858 1.4248 1.4645	0.1000 0.1050 0.1101 0.1151 0.1201 0.1452 0.1705 0.1958 0.2214 0.2472 0.2732 0.2995 0.3261 0.3530 0.3803 0.4080 0.4362 0.4648 0.4938 0.5234 0.5536 0.5843 0.6156 0.6476 0.6802 0.7134 0.7474 0.7821 0.8176 0.8538 0.8909 0.9287 0.9674 1.0070 1.0475 1.0888 1.1311 1.1743 1.2185 1.2637 1.3099 1.3475 1.3858 1.4248 1.4645

2) Изменим начальные условия и интервал интегрирования:

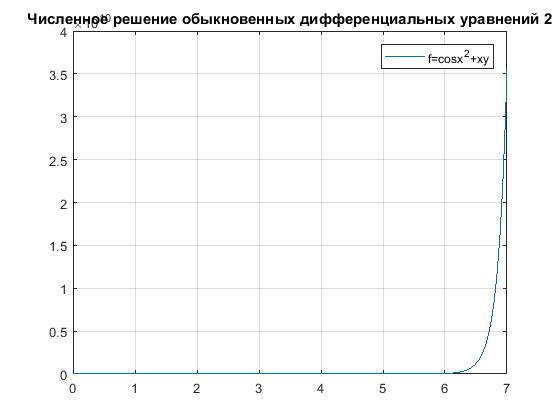
Интервал от 0 до 7:

tspan=[0 7];

x0=0.1;

[x,y] = ode45(@fun,tspan,x0)

plot(x,y)

grid on

title('Численное решение обыкновенных дифференциальных уравнений 2');

legend('f=cosx^2+xy')

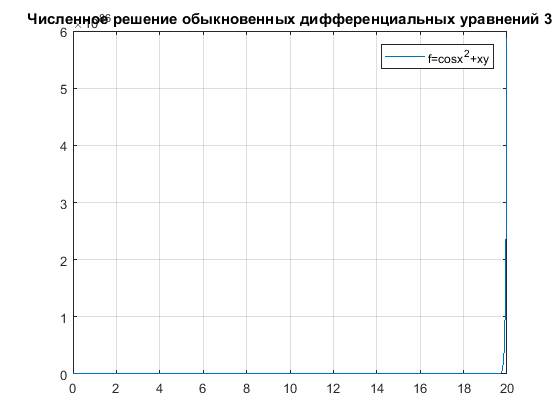
Интервал от 0 до 20:

tspan=[0 20];

x0=0.1;

[x,y] = ode45(@fun,tspan,x0)

plot(x,y)

grid on

title('Численное решение обыкновенных дифференциальных уравнений 3');

legend('f=cosx^2+xy')

3)Применение функций od23 и ode113:

ode23:

tspan=[0 1];

x0=0.1;

[x,y] = ode23(@fun,tspan,x0)

plot(x,y)

grid on

title('ode23');

legend('f=cosx^2+xy')

ode113:

tspan=[0 1];

x0=0.1;

[x,y] = ode113(@fun,tspan,x0)

plot(x,y)

grid on

title('ode113');

legend('f=cosx^2+xy')

ode23

ode113

0 0.0080 0.0480 0.1480 0.2480 0.3480 0.4480 0.5480 0.6480 0.7480 0.8480 0.9480 1.0000

0.1000 0.1080 0.1482 0.2502 0.3562 0.4681 0.5879 0.7174 0.8581 1.0117 1.1794 1.3626 1.4645

0 0.0008 0.0024 0.0055 0.0119 0.0245 0.0498 0.1004 0.2004 0.3004 0.4004 0.5004 0.6004 0.7004 0.8004 0.9004 1.0000

0.1000 0.1008 0.1024 0.1055 0.1119 0.1245 0.1500 0.2012 0.3051 0.4140 0.5298 0.6544 0.7896 0.9369 1.0977 1.2734 1.4645