Решить задачи со своими измененными данными используя примеры задач

Решить задачи со своими измененными данными используя примеры задач

Примеры решения задач

Пример 1. Дано уравнение движения точки: S = 0,36t² + 0,18t. Определить скорость точки в конце третьей секунды движения и среднюю скорость за первые 3 секунды.

1. Уравнение скорости

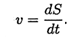
S' = 2 • 0,36t + 0,18; v = 0,72t + 0,18.

2. Скорость в конце третьей секунды (t = Зс) v₃ = 0,72 * 3 + 0,18 = 2,34м/с.

3.Средняя скорость V_ср = dS/dt = (0,36 • 3²+ 0,18 * 3)/3 = 1,26 м/с.

Пример 2. Точка движется по кривой радиуса г = 10 м согласно уравнению S = 2,5t² + 1,2t + 2,5 (рис. 9.6).

Определить полное ускорение точки в конце второй секунды движения и указать направление касательной и нормальной составляющих ускорения в точке М.

1.Касательное ускорение определяется как a_t = dV/dt

Уравнение скорости: v = dS/dt

Скорость будет равна v = 2 * 2,5t + 1,2; v = 5t + 1,2 (м/с).

Касательное ускорение: а_t = v' = 5 м/с².

Вывод: касательное ускорение не зависит от времени, оно постоянно.

2. Нормальное ускорение: а_п = v²/r

Скорость на второй секунде будет равна v₂= 5*2 + 1,2 = 11,2 м/с.

Величина нормального ускорения: а_п₂ = (11,2)²/10 = 12,54 м/с² .

3. Полное ускорение:

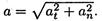
Полное ускорение в конце второй секунды:

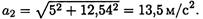
4. Нормальное ускорение направлено перпендикулярно скорости к центру дуги.

Касательное ускорение направлено по касательной к кривой и совпадает с направлением скорости, т. к. касательное ускорение — положительная величина (скорость растет).

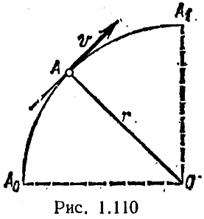
Пример 3. По дуге, равной ¹/₄ длины окружности радиуса г = 16м (рис. 1.110), из положения А₀ в положение A₁ движется точка согласно уравнению s = πt². Определить скорость точки в момент, когда она проходит середину длины дуги A₀A₁, и в момент достижения положения A₁.

Если длина дуги А₀А₁ равна ¹/₄ длины окружности, то середина дуги А находится от начала отсчета А₀ на расстоянии ¹/₈ окружности, т, е.

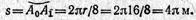
2. Из заданного уравнения движения s = πt²находим, что точка после начала движения достигает середины дуги через промежуток времени

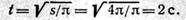
3. Продифференцировав уравнение движения, найдем уравнение скорости:

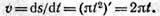
4. Подставив значение t = 2 с в уравнение скорости, найдем

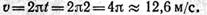
5. Проводим в точке А (середину дуги A₀A₁) касательную к траектории и изобразим вектор скорости v (рис. 1.110).

Скорость точки в конце траектории (в положении A₁) рекомендуется найти самостоятельно. (Ответ: 17,8 м/с.)