Учебная дисциплина Техническое черчение

Учебная дисциплина Техническое черчение

Гр № 11

Занятие № 12

Дата 30 сентября 21г

Тема занятия«Сопряжения»

Цели работы:изучить материал, связанный видами спряжений, знать способы деления окружности на равные части.

Изучение материала:

Контуры очертания большинства деталей состоят из линий, плавно переходящих одна в другую, и поэтому, выполняя чертежи технических изделий, приходится соединять между собой линии различного вида (прямые, дуги, окружности). На рисунке 1а показано изображение рычага. Его внешний контур состоит из ряда отдельных линий, плавно сопрягающихся между собой. Видно, что дуга 1 переходит в дугу 2, дуга 2 в дугу 3, дуга 3 в дугу 4,

дуга 4 в дугу 5, дуга 5 в прямую линию 6, линия 6 в дугу 7, и последняя дуга в прямую линию 8 (Рис. 1б).

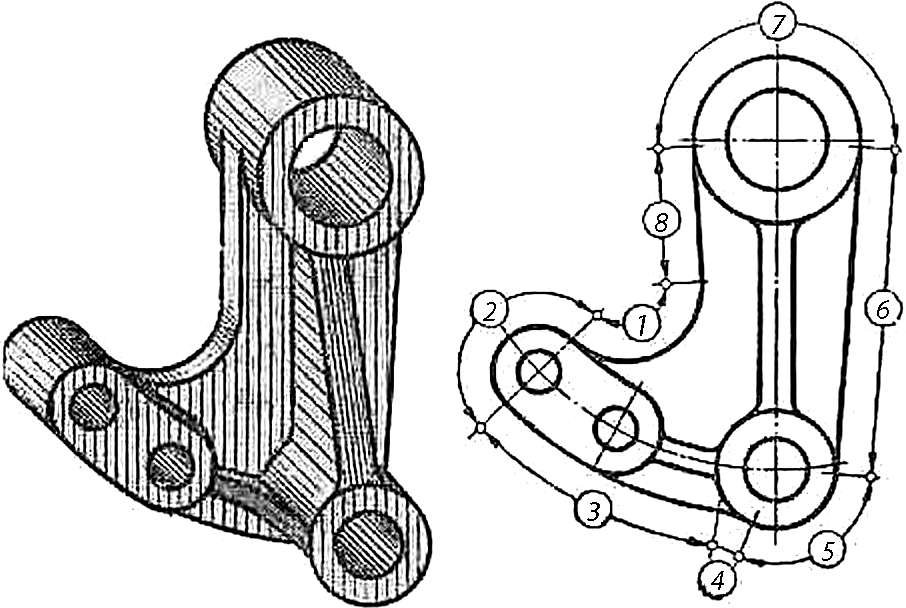
а) б)

Рисунок 1 - Контур детали машин

СОПРЯЖЕНИЕ

Плавный переход одной линии в другую называют касанием, а точку, в которой происходит касание, точкой касания. Плавный переход одной линии в другую при помощи промежуточной линии называют сопряжением. Чаще всего промежуточной линией служит дуга окружности.

1.1. Общие положения сопряжений

Построение сопряжений линий основано на понятиях о геометрических местах, о касательных прямых к окружности, и окружностях, касательных к другой окружности.

Следующие положения, известные из геометрии: 1). Плавный переход

двух линий может быть осуществлен только при условии их соединения (сопряжения) в точке касания, которую называют и «точкой перехода» и

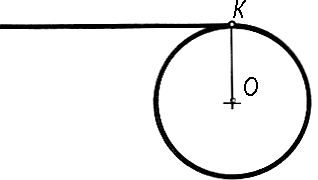
«точкой сопряжения». На рисунке 2 изображена

точка сопряжения К.

Значит, при построении сопряжений следует иметь в виду, что переход от

Рисунок 2 -

Точка сопряжения К

прямой к окружности будет плавным, если прямая касается окружности. В этом случае точка сопряжения А лежит на радиусе, перпендикулярном касательной прямой m (Рис. 3а).

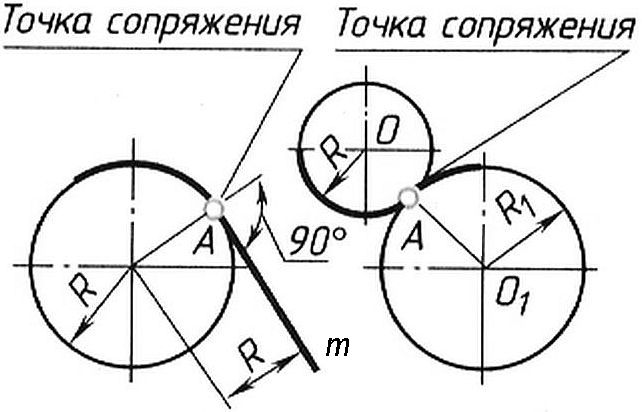
а) б)

Рисунок 3 - Точки сопряжений

2). Переход от одной окружности (дуги) к другой будет плавным, если окружности касаются (Рис. 3б). Точка сопряжения К находится на прямой, соединяющей центры окружностей (Рис. 4). Прямая, соединяющая центры их О₁ и О₂ называется линией центров. Касание окружностей может быть внешним (Рис. 4а) и внутренним (Рис. 4б).

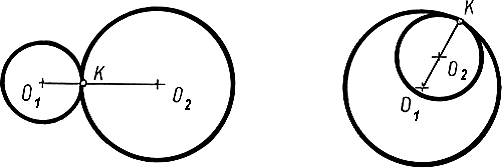
а) б)

Рисунок 4 - Переход между окружностями

Следовательно, для сопряжения двух окружностей (дуг) необходимо, чтобы центры окружностей (дуг) лежали на одной прямой, проходящей через точку сопряжения и перпендикулярной к общей касательной m этих окружностей (дуг) (Рис. 5).

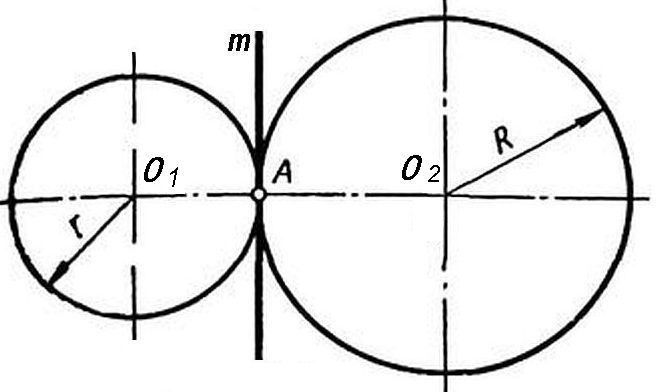
Рисунок 5 - Касательная двух окружностей

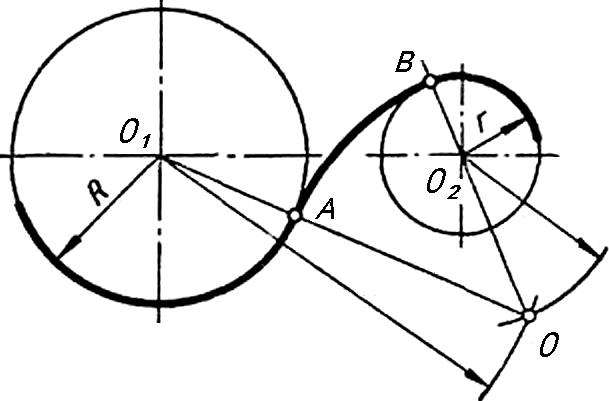
В теории сопряжений применяются специфические термины:

- точки О или О_с - центры сопряжений;

- точки О₁, О₂ - центры заданных окружностей;

- R или R_с - радиус сопряжений;

- R, R₁, R₂, r - радиусы заданных окружностей;

- точки А и В, К₁, К₂ - точки сопряжений;

- дуга АВ - дуга сопряжения и т.д. (Рис. 6).

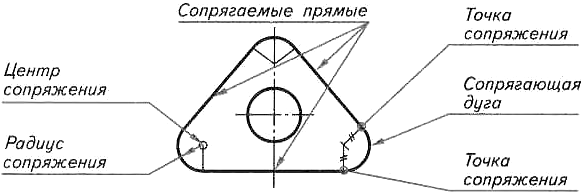
Рисунок 6 - Элементы сопряжений

Дуги окружностей, при помощи которых выполняется сопряжение, называют дугами сопряжения. Для построения сопряжений надо найти центры, из которых проводят эти дуги, то есть центры сопряжений. Надо определить также точки, в которых одна линия переходит в другую (точки сопряжений). Таким образом, для построения любого сопряжения надо найти центр сопряжения, точки сопряжений, знать радиус сопряжения.

Выделим общий алгоритм построения:

- найти центр сопряжения;

- найти точки сопряжения, в которых дуга сопряжения переходит в сопрягаемые линии;

- построить дуги сопряжения, значит соединить точки сопряжения заданным радиусом сопряжения.

Далее из всего многообразия сопряжений различных линий рассмотрим наиболее распространенные:

1). Сопряжение двух прямых линий.

2). Сопряжение прямой линии и окружности (дуги). 3). Сопряжение двух окружностей (дуг).

1.2. Геометрическое место

Решение задач на построение сопряжений основано на методе геометрических мест. Геометрическим местом точек называется фигура, которая состоит из всех точек плоскости, обладающих определенным свойством.

Геометрическим местом (ГМ) центров окружности сопряжения касательной к прямой а является прямая, параллельная данной и отстоящей от нее на расстоянии радиуса окружности сопряжения (Рис. 7а). Геометрическим местом центров окружности сопряжения, касательной к сопрягаемой окружности, является окружность, радиус которой равен сумме радиусов окружности сопряжения и окружности сопрягаемой для внешнего сопряжения (Рис. 7б) и разности радиусов этих окружностей (Рис. 7в) для внутреннего сопряжения.

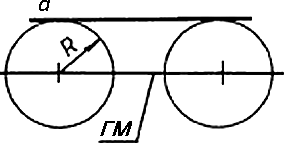
а)

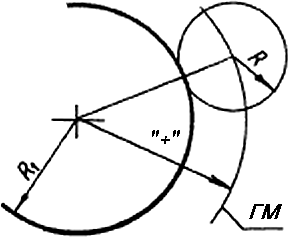
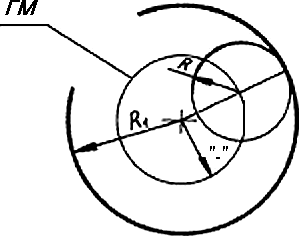
б) в)

Рисунок 7 - Геометрическое место

Например, алгоритм решения задач на построение сопряжений двух линий при заданном радиусе сопряжения может быть сформулирован так:

- Построить геометрическое место центров окружности сопряжения для одной из сопрягаемых линий.

- Построить аналогичное геометрическое место центров для второй сопрягаемой линии.

- Точка пересечения построенных геометрических мест является центром сопряжения.

- Определить точку сопряжения на первой из сопрягаемых линий.

- Определить точку сопряжения на второй из сопрягаемых линий.

- В границах между точками сопряжений провести дугу сопряжения.

1.3. Построение касательной

При сопряжении всегда имеются две точки перехода и через каждую из них можно провести по одной общей касательной.

Рассмотрим несколько случаев построения касательной:

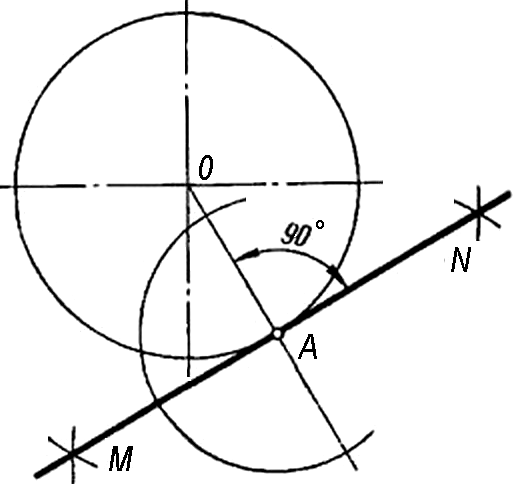
- Построение касательной к окружности в заданной на ней точке. Через точку А и центр О проводят прямую и в точке А восстанавливают к ней перпендикуляр (Рис. 8).

- Построение касательной к окружности из точки А вне окружности. Центр окружности О и точку А соединяют прямой (Рис. 9). Отрезок OA принимают за диаметр вспомогательной

окружности. Разделив отрезок OA пополам, получают точку О₁. Из точки О₁ описывают
Рисунок 8 - Построение касательной к окружности

окружность радиусом O₁A, которая пересекает заданную окружность в точках касания В и С.

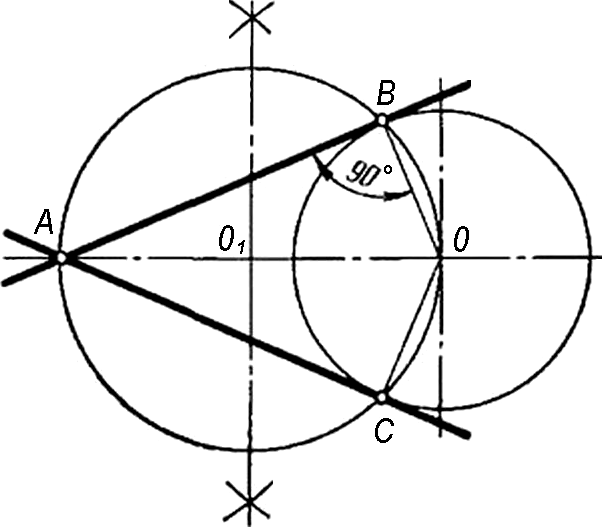
Рисунок 9 - Построение касательной

- Построение касательных окружностей. При внешнем касании окружностей центры О₁ и О₂ расположены на расстоянии R +r друг от друга. Точка касания лежит на прямой, соединяющей центры О₁ и О₂, а общая касательная MN к этой прямой в точке А перпендикулярна (Рис. 10а). При внутреннем касании расстояние между центрами касающихся окружностей равно разности радиусов R - r. Точка касания А расположена на продолжении прямой, соединяющей центры О₁ и О₂ (Рис. 10б).

- Построение общей внешней касательной к двум окружностям. Из центра О₁ большей окружности описывают окружность радиусом R - r (Рис. 11а). Находят середину отрезка О₁О₂ - точку О₃ и из нее проводят окружность радиусом О₁О₃. Обе проведенные окружности пересекаются в точках А и В. Точки О₁ и В соединяют прямой и в пересечении ее с окружностью радиуса R определяют точку касания D (Рис. 11б). Из точки О₂ параллельно прямой О₁D проводят линию до пересечения с окружностью радиуса r и получают вторую точку касания С.

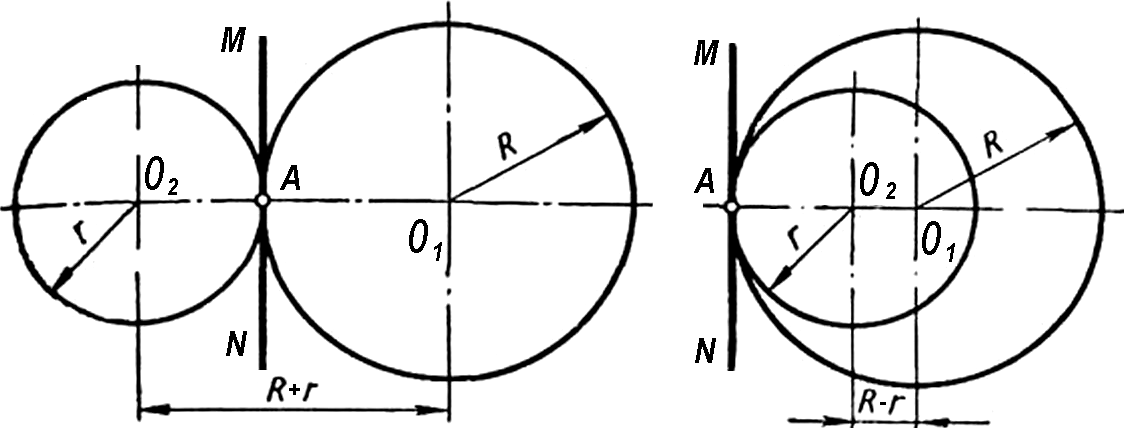
а) б)

Рисунок 10 - Построение касательных окружностей

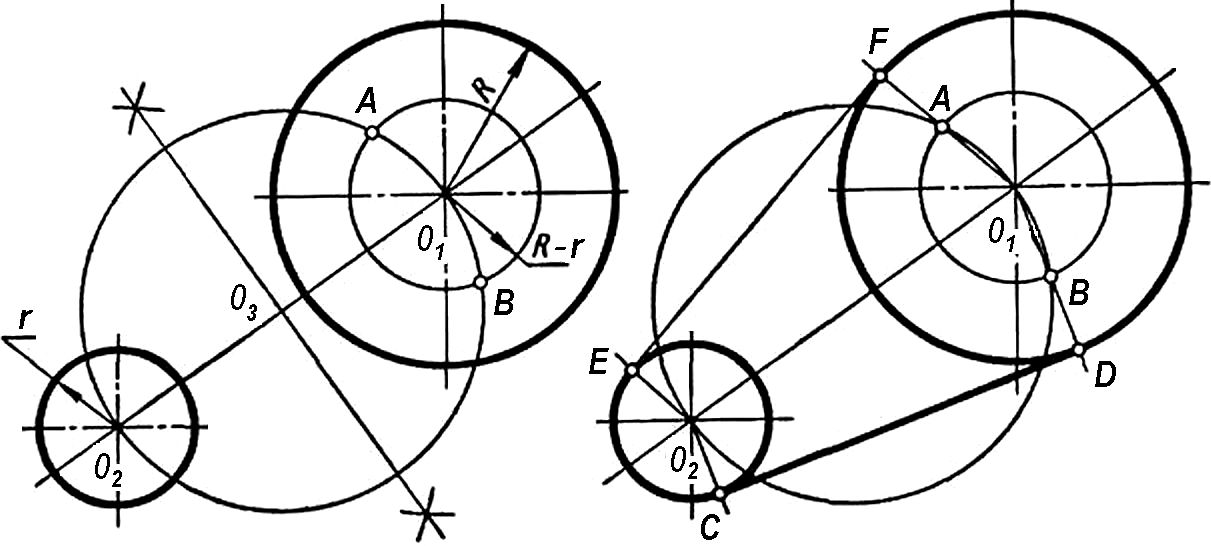
а) б)

Рисунок 11 - Построение общей внешней касательной

- Построение общей внутренней касательной к двум окружностям. Из центра любой окружности описывают окружность радиусом R + r (Рис. 12а). Разделив отрезок О₁О₂ пополам, получают точку О₃. Из точки О₃ описывают окружность радиусом О₁О₃ и отмечают точки А и В пересечения вспомогательных окружностей. Соединив точки О₁ и А прямой (Рис. 12б), получают точку касания D. Через точку О₂, проводят прямую, параллельную О₁A, и получают вторую точку касания С.

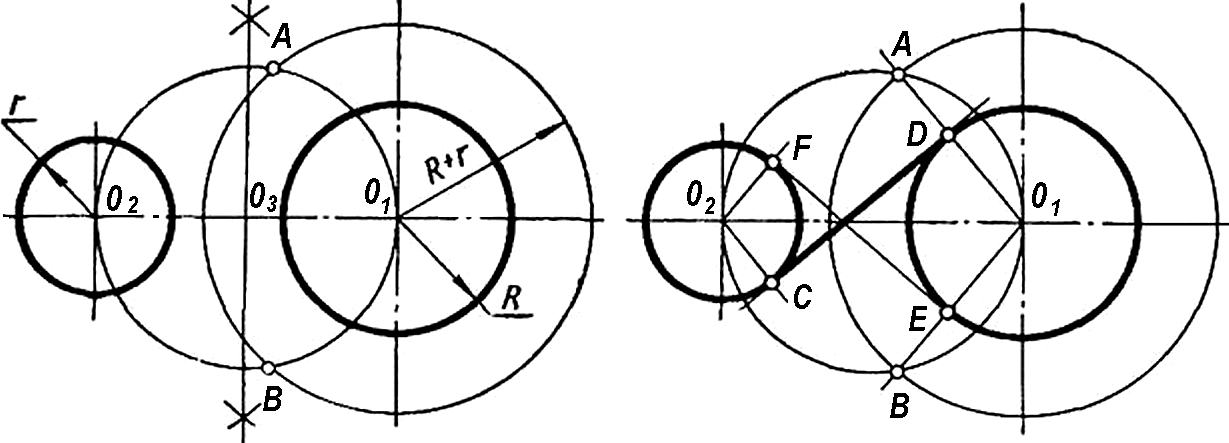
а) б)

Рисунок 12 - Построение общей внутренней касательной

1.4. Сопряжение двух прямых при задании одной из точек сопряжения

В том случае, когда задана точка сопряжения К₁ на одной из прямых находят центр О_С, радиус R и точку сопряжения К₂ на второй прямой (Рис. 13). Для этого необходимо восстановить из К₁ перпендикуляр (См. рис. 2, 3а) и провести биссектрису угла. Точка О_С пересечения является центром сопряжения, а О_СК₁ - радиусом сопряжения. Опускают из

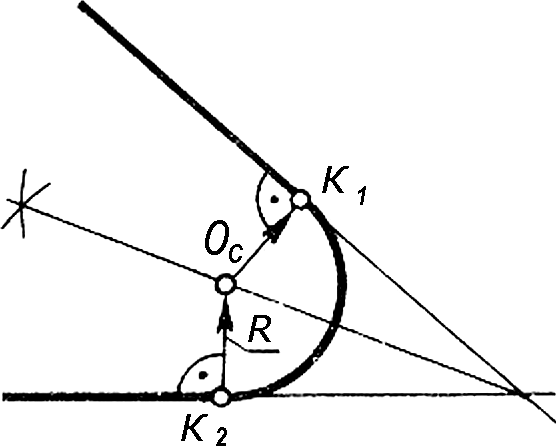
Рисунок 13 - Сопряжение двух прямых

центра О_С перпендикуляр к другой стороне угла, получают точку сопряжения К₂. Между точками К₁ и К₂ проводят сопрягающую дугу радиусом О_СК₁.

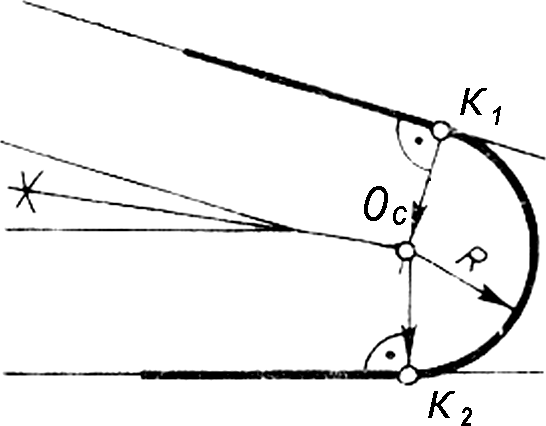
Рисунок 14 -

Точка сопряжения на стороне угла

В случае, когда точка сопряжения К₁ дана на стороне угла, вершина которого находится за пределами чертежа (Рис. 14), выполняют, применив правила геометрических построений, биссектрису вспомогательного угла, стороны которого параллельны сторонам заданного угла и находятся на равных расстояниях от них.

1.5. Сопряжение двух пересекающихся прямых

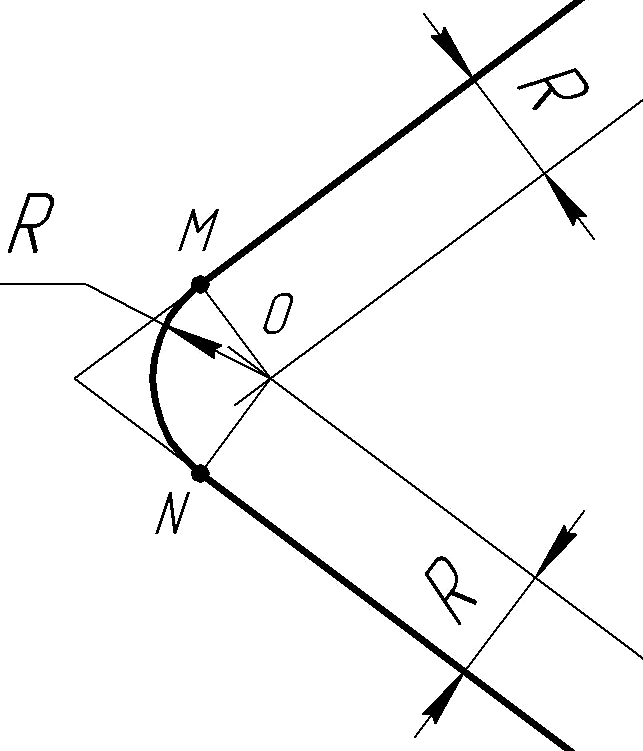Рассмотрим построение сопряжений пересекающихся прямых линий (сторон угла) дугой заданного радиуса R. На рисунке

15 выполнено построение сопряжения дугой сторон острого угла, а на рисунке 16а - сторон тупого угла, на рисунке 16б - прямого

угла. Рисунок 15 -

Сопряжение сторон острого угла

Сопряжение выполняется следующим образом:

- Параллельно сторонам угла на расстоянии, равном радиусу дуги R, проводят две вспомогательные прямые.

- Точка пересечения этих линий будет центром дуги радиуса

R, то есть центром сопряжения О.

- Из центра О описывают дугу, плавно переходящую в прямые линии - стороны угла.

- Дугу заканчивают в точках М и N - это точки сопряжения, они являются основаниями перпендикуляров, опущенных из центра сопряжения О на стороны угла.

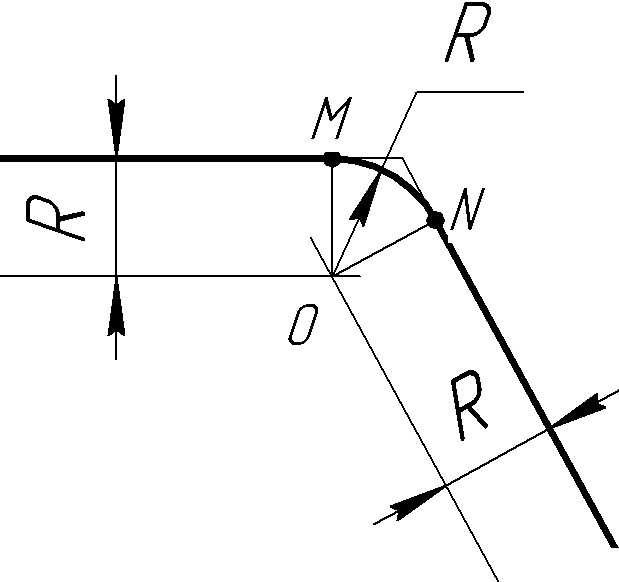
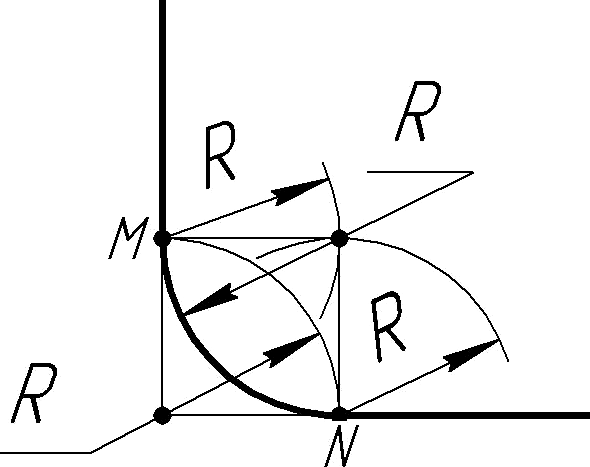
а) б)

Рисунок 16 - Построение сопряжений сторон углов

При выполнении контурных очертаний технических деталей применяются правила построения сопряжений сторон углов дугами окружностей. На рисунке 17а для изображения скобы показано применение сопряжений сторон острых углов, на рисунке 17б для вычерчивания прихвата использованы плавные переходы сторон тупых углов, на рисунке 17в для крышки - переходы прямых углов.

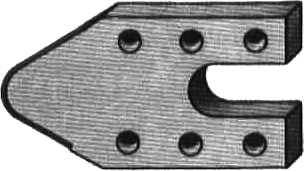
а) б) в)

Рисунок 17 - Практическое применение сопряжений углов

1.6. Применение геометрических построений

Рисунок 18 -

Анализ контура изображения детали

Чтобы изготовить из металлического листа деталь, например шаблон, изображенный на рисунке 18, необходимо прежде очертить на металле его контур, то есть сделать разметку. Между оформлением разметки и чертежа много общего. При выполнении разметки или чертежа надо определить, какие следует при этом применить геометрические построения, то есть провести анализ графического состава изображений. В результате анализа устанавливаем, что

вычерчивание контура шаблона слагается в основном из построения угла 60° и сопряжений острого и тупого углов дугами заданных радиусов.

На рисунке 19 показаны эти построения.

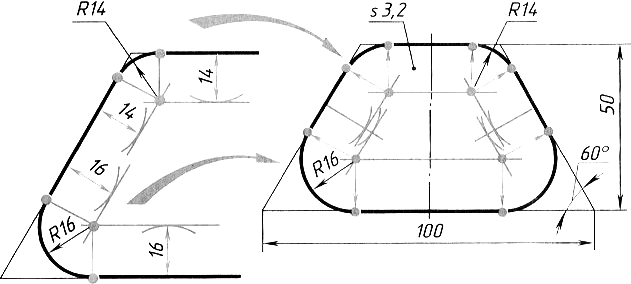
Рисунок 19 - Геометрические построения шаблона

1.7. Сопряжение параллельных прямых

В случае, когда задана точка сопряжения К₁ на одной из параллельных прямых (Рис. 20), определение точки сопряжения К₂ на второй прямой осуществляется с помощью перпендикуляра, восстановленного из точки

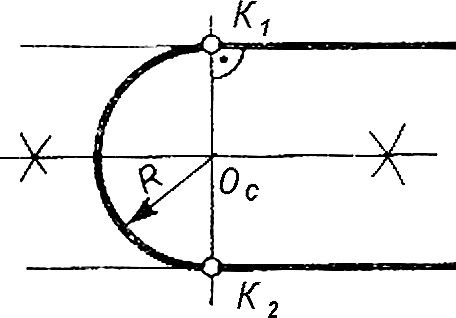К₁. Центр сопряжения О_С и радиус сопряжения R сопрягающей дуги находят, разделив отрезок К₁К₂ пополам. Из центра О_С проводят сопрягающую дугу, соединяющую две точки К₁ и К₂ радиусом R = О_С К₁ = О_С К₂.

Точки сопряжения К₁ и К₂ могут быть даны на параллельных

прямых, направленных от них в разные стороны. Такие точки сопряжения могут быть расположены на одном или на разных

Рисунок 20 - Сопряжение параллельных прямых

перпендикулярах к параллельным прямым.

Сопряжение параллельных прямых при расположении точек сопряжения на одном перпендикуляре к ним выполняют двумя дугами одинаковых радиусов, равных 1/4 расстояния между ними (Рис. 21а). Применив известные геометрические построения и правила для разделения отрезка перпендикуляра К₁К₂ пополам, определяют точку К₃ касания двух сопрягающих (соединяющих) дуг.

Центры О_С1 и О_С2 сопрягающих дуг находят в серединах каждого из отрезков К₁К₃ и К₂К₃. Из центров сопряжений О_С1 и О_С2 проводят две сопрягающие дуги радиуса R_С = К₁К₂ / 4.

Случаи, когда точки сопряжения заданы на разных перпендикулярах к параллельным прямым, которые направлены в разные стороны, наглядно иллюстрирует рисунок 21б.

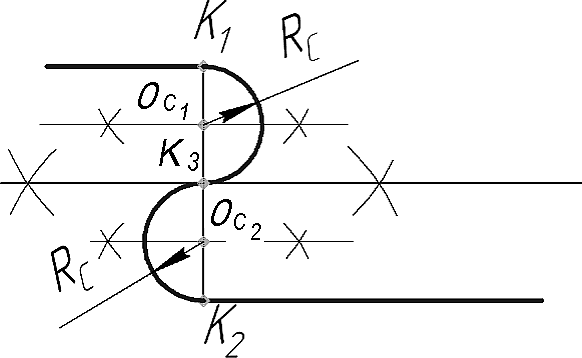а)

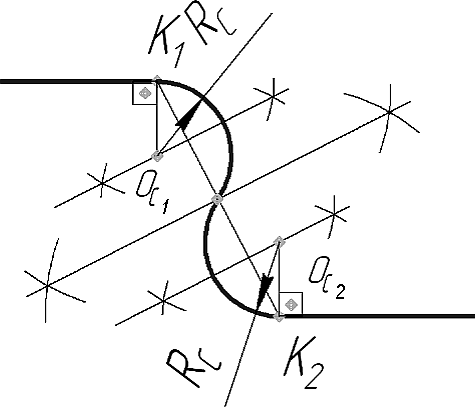б)

Рисунок 21 - Сопряжения параллельных прямых, направленных в разные стороны

1.8. Сопряжение дуги окружности и прямой дугой заданного радиуса

При построении сопряжений прямых с дугами окружностей различают случаи внешнего и внутреннего касания.

На рисунке 22 показан случай внешнего касания. Для определения центра О_С дуги сопряжения окружности и прямой проводят вспомогательную прямую параллельно заданной прямой на расстоянии, равном радиусу R_С дуги сопряжения. Из центра О₁ заданной окружности проводят вспомогательную дугу радиусом R₁ + R_С до пересечения с вспомогательной прямой. Точка пересечения и есть центр О_С дуги сопряжения. Точку сопряжения К₂ определяют, опустив из центра О_С перпендикуляр на заданную прямую. Точку сопряжения К₁ определяют в пересечении линии центров О₁О_С с заданной окружностью. Завершают построение проведением сопрягающей дуги R_С между точками К₁ и К₂.

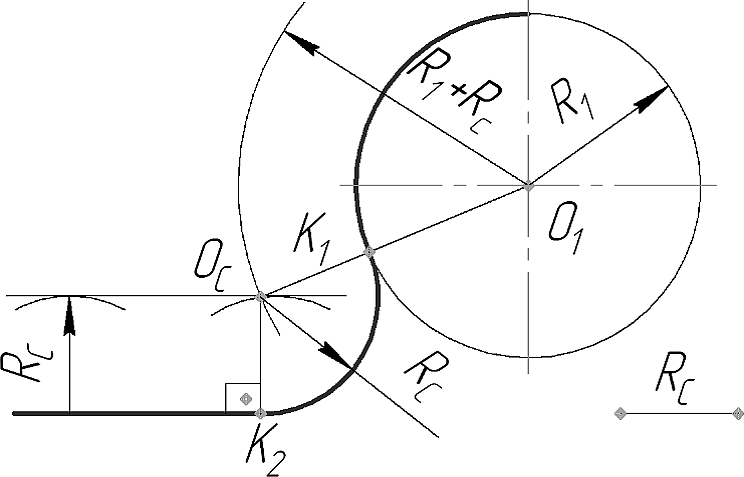
Рисунок 22 - Внешнее касание окружности и прямой

При внутреннем касании прямая может пересекать окружность или проходить вне ее. На рисунке 23 изображено построение сопряжения дуги окружности радиуса R₁ с прямой, пересекающей эту окружность. Для нахождения центра дуги сопряжения О_С

на расстоянии, равном радиусу сопряжения R_С, проводят вспомогательную прямую, параллельную данной, и вспомогательную дугу окружности радиуса R₁ - R_С, концентрическую данной. На их взаимном пересечении определяется точка пересечения, которая и есть центр О_С дуги сопряжения. Точки К₁ и К₂ находятся построением, показанном на рисунке.

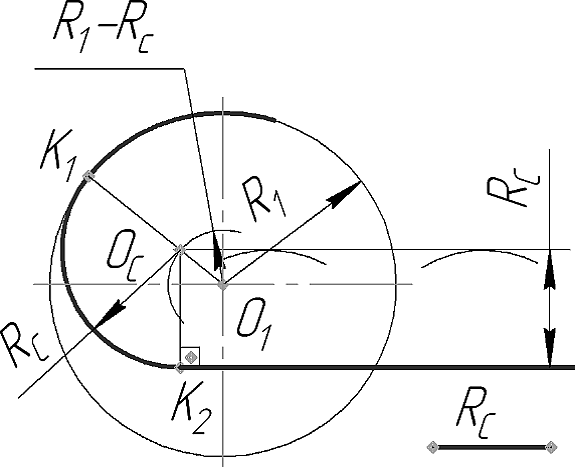
Рисунок 23 - Внутреннее касание окружности и прямой

1.9. Сопряжение дуги окружности с прямой в случае задания точки сопряжения

Точка сопряжения может находиться как на заданной окружности, так и на заданной прямой. Рассмотрим варианты сопряжения, когда точка сопряжения К₁ находится на заданных окружностях. На рисунке 24 показано внешнее сопряжение окружности с прямой и для этого определяют центр О_С и радиус R_C дуги сопряжения.

Построение сопряжения приводит к скруглению угла при заданной точке сопряжения К₁:

- проводят касательную к окружности в точке К₁

перпендикулярно к радиусу О₁К₁ (См. рис. 2, 3а);

- далее выполняют построения, как было показано на рисунке 13.

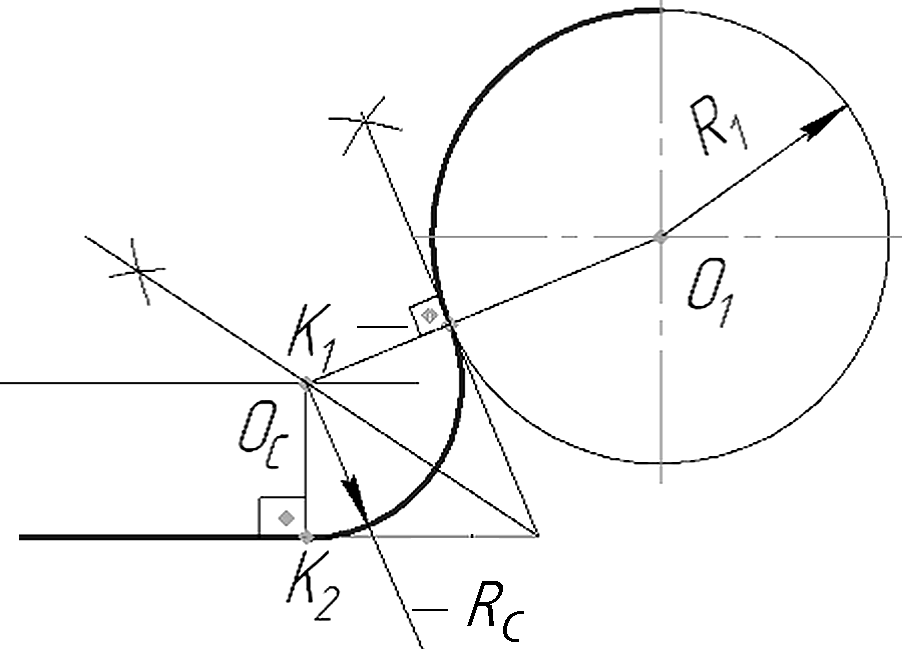
Рисунок 24 - Внешнее сопряжение окружности с прямой

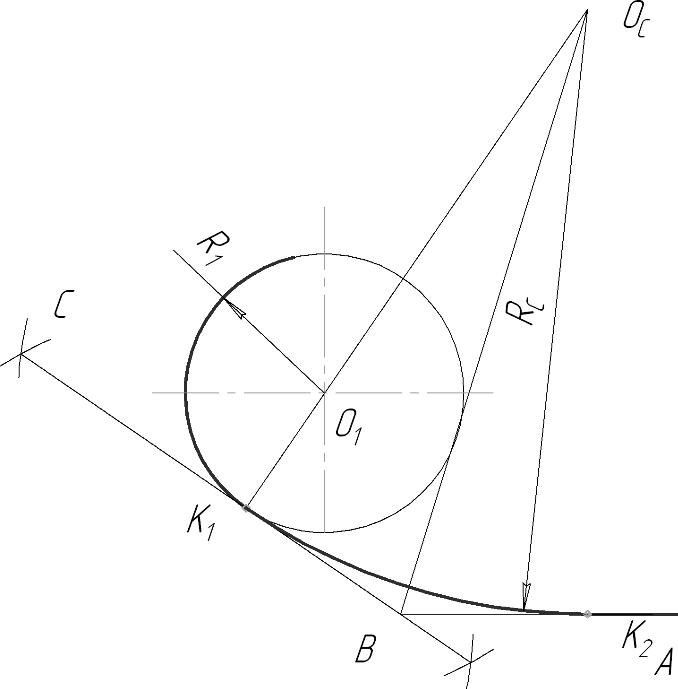
Аналогично строят внутреннее сопряжение окружности с прямой в случаях, когда прямая пересекает окружность (Рис. 25а), или проходит вне ее (Рис. 25б).

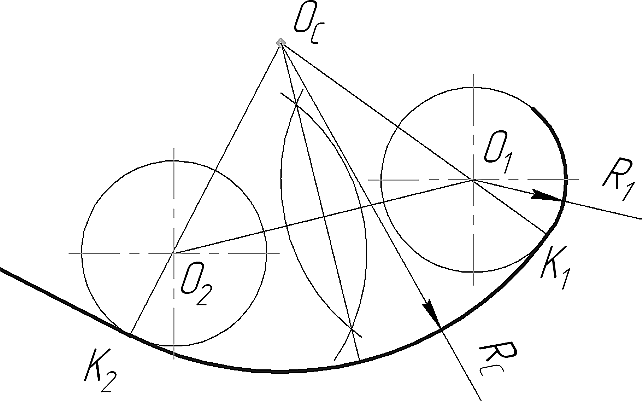
В том случае, когда точка сопряжения К₂ находится на заданной прямой, для выполнения сопряжения определяют положение центра О_С и, используя изученные положения (См. рис. 4), находят точку сопряжения К₁ на заданной окружности. Далее из точки К₂ к заданной прямой восстанавливается перпендикуляр, на котором для внешнего сопряжения (Рис. 26а) от точки К₂ радиус R₁ откладывают вниз от заданной прямой, а при внутреннем сопряжении (Рис. 26б) вверх, в результате определяют центр О₂ вспомогательной окружности. Проводим линию центров О₁О₂. Центр О_С дуги сопряжения определяется в пересечении серединного перпендикуляра линии центров с перпендикуляром, проведенным через точку К₂. Точка сопряжения К₁ находится в пересечении линии центров О₁О_С с заданной окружностью. Завершаем построение проведением сопрягающей дуги R_С между точками К₁ и К₂.

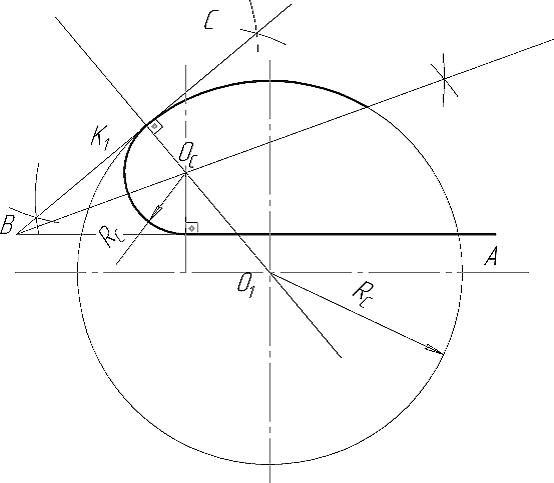
а)

б)

Рисунок 25 - Внутреннее сопряжение окружности с прямой

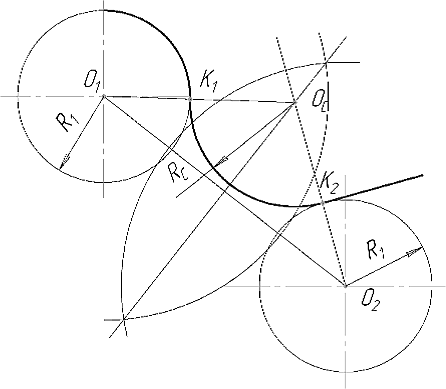
а)

б)

Рисунок 26 - Сопряжение окружности с прямой

1.10. Практическое применение сопряжений прямой с окружностью

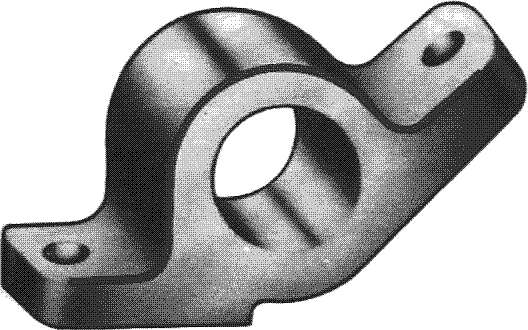
Рисунок 27 - Кронштейн

На рисунке 27 изображен кронштейн. При выполнении изображения контура этой детали необходимо выполнить следующие построения:

- Для сопряжения дуги окружности радиуса R с прямой АВ дугой радиуса r вычерчивают дугу окружности радиуса R (Рис. 28) и прямую АВ.

- Параллельно заданной

прямой на расстоянии, равном радиусу r сопрягающей дуги, проводят прямую ab. Из центра О проводят дугу окружности радиусом, равным сумме радиусов R и r, до пересечения ее с прямой линией ab в точке О₁. Точка О₁ - центр дуги сопряжения.

- Точку сопряжения с находят на пересечении прямой ОО₁ с дугой данной окружности радиуса R, а точка с₃ является основанием перпендикуляра, опущенного из центра О₁ на данную прямую АВ.

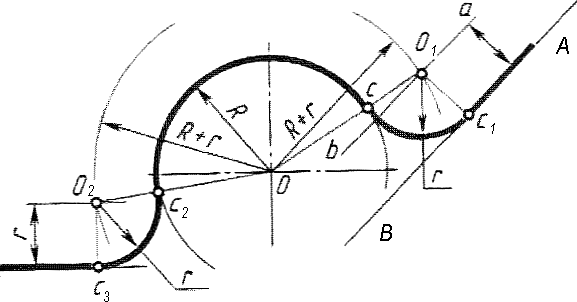
Рисунок 28 - Выполнение контура кронштейна

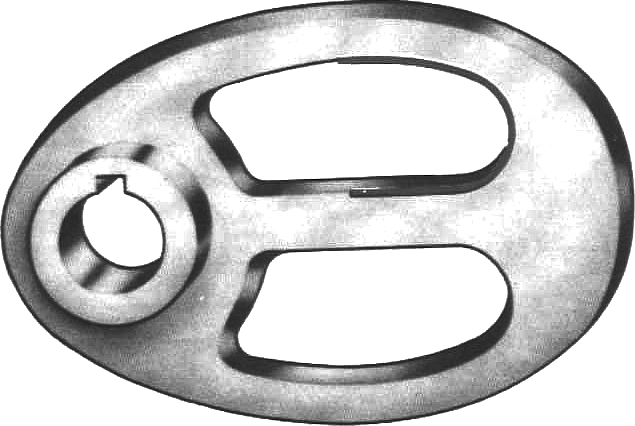
Рисунок 29 - Маховик

На рисунке 29 изображен маховик, и здесь имеется сопряжение дуги с прямой. Такое сопряжение прямой, проходящей через точку О, с дугой окружности радиуса R выполняют, как показано на рисунке 30.

Дуга сопряжения имеет радиус r. Центр дуги сопряжения О₁ находят на пересечении вспомогательной

прямой, проведенной параллельно данной прямой на расстоянии r, с дугой вспомогательной окружности, описанной из точки О радиусом, равным R - r. Точка сопряжения с₁ является основанием перпендикуляра, опущенного из точки О₁ на данную прямую. Точку сопряжения с находят на пересечении прямой ОО₁ с данной сопрягаемой дугой.

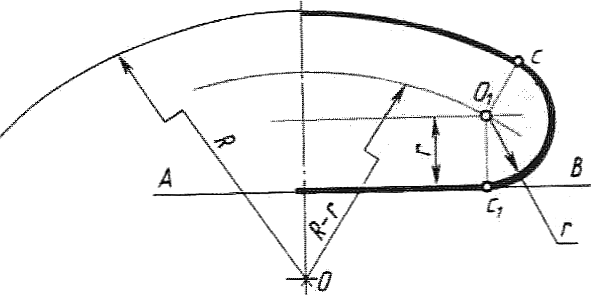
Рисунок 30 - Вычерчивание контура маховика

1.11. Виды сопряжений окружностей

Заметим, что сопряжение окружностей (дуг) может быть внешним (Рис. 31а), внутренним (Рис. 31б) и смешанным (Рис. 31в). У внешнего сопряжения центры двух сопрягаемых окружностей лежат вне сопрягающей окружности. У внутреннего сопряжения

центры сопрягаемых окружностей лежат внутри сопрягающей окружности. При смешанном сопряжении центр одной окружности лежит вне сопрягающей окружности, а центр другой окружности лежит внутри ее.

а)

б)

в)

Рисунок 31 - Виды сопряжений окружностей

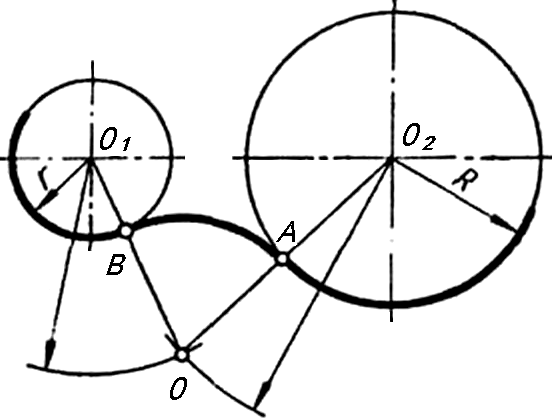
Покажем наглядно алгоритм построения сопряжения двух окружностей. На рисунке 32 показано определение центра сопряжения двух окружностей.

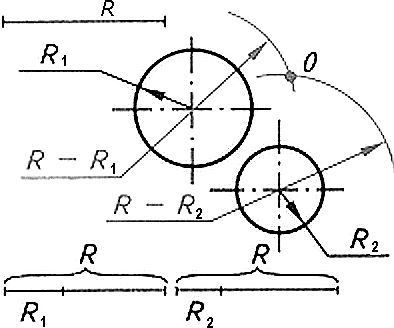
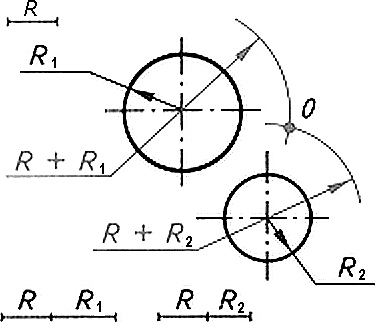
Рисунок 32 - Определение центра сопряжений

На рисунке 33 изображено построение точек сопряжения, а на рисунке 34 - построение сопрягающей дуги заданного радиусаю

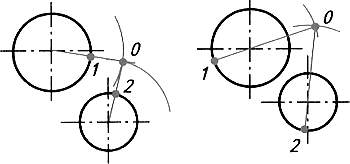
Рисунок 33 - Определение точек сопряжения

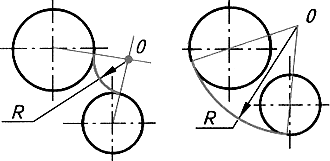
Рисунок 34 - Построение сопрягающей дуги

1.12. Построение сопряжения дуги с дугой

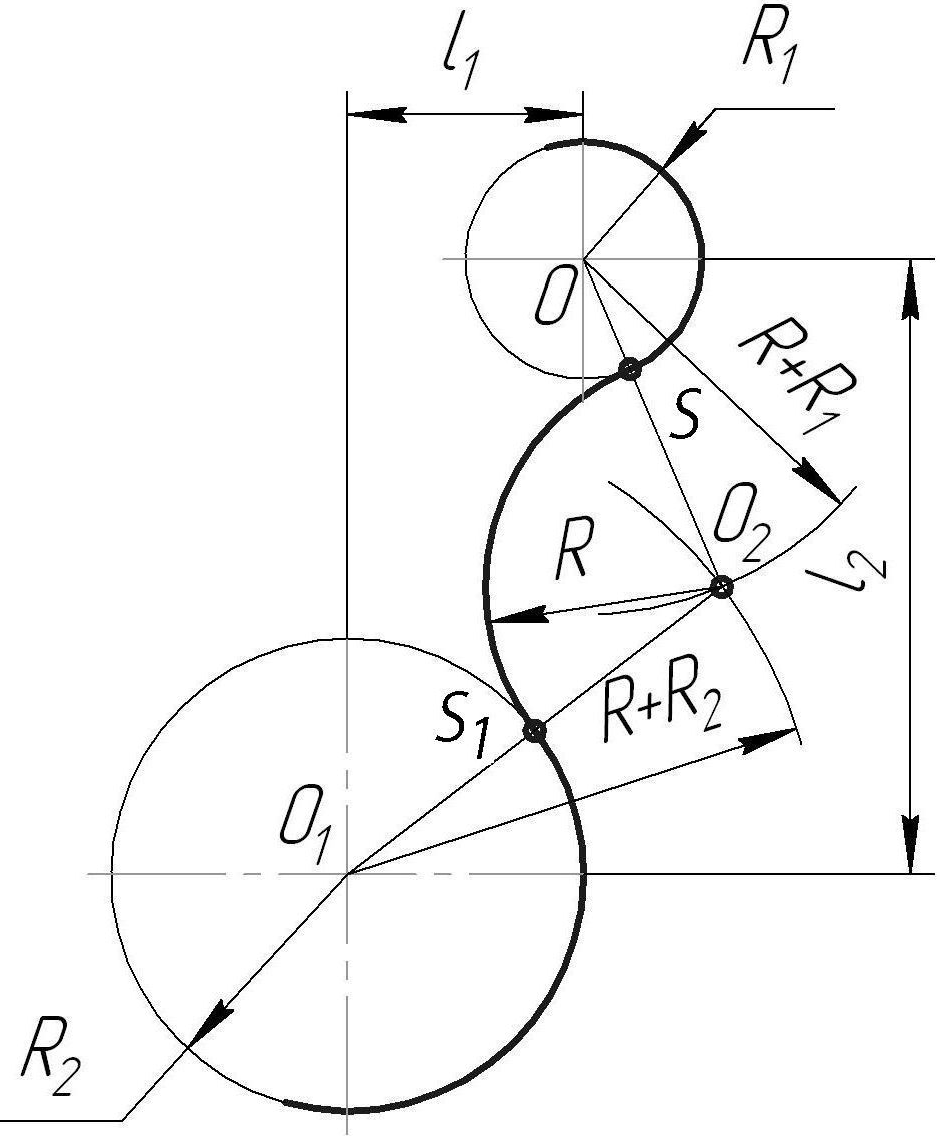
На рисунке 35 показаны изображение и вычерчивание детали с применением внутреннего (Рис. 36а) и внешнего (Рис. 36б) сопряжений двух дуг окружностей.

Построение внутреннего сопряжения показано на рисунке 36а. По заданным расстояниям между центрами l₁ и l₂ на чертеже намечают центры О и О₁, из которых описывают сопрягаемые дуги радиусов R₁ и R₂. Из центра О₁ проводят вспомогательную дугу окружности радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R₂, а из центра О - радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R₁. Вспомогательные дуги пересекутся в точке О₂, которая и будет искомым центром сопрягающей дуги.

Для нахождения точек сопряжения точку О₂ соединяют с точками О и О₁ прямыми линиями. Точки пересечения продолжения прямых О₂О и О₂О₁ с сопрягаемыми дугами являются искомыми точками сопряжения - точки S и S₁. Радиусом R из центра О₂ проводят сопрягающую дугу между точками сопряжения S и S₁.

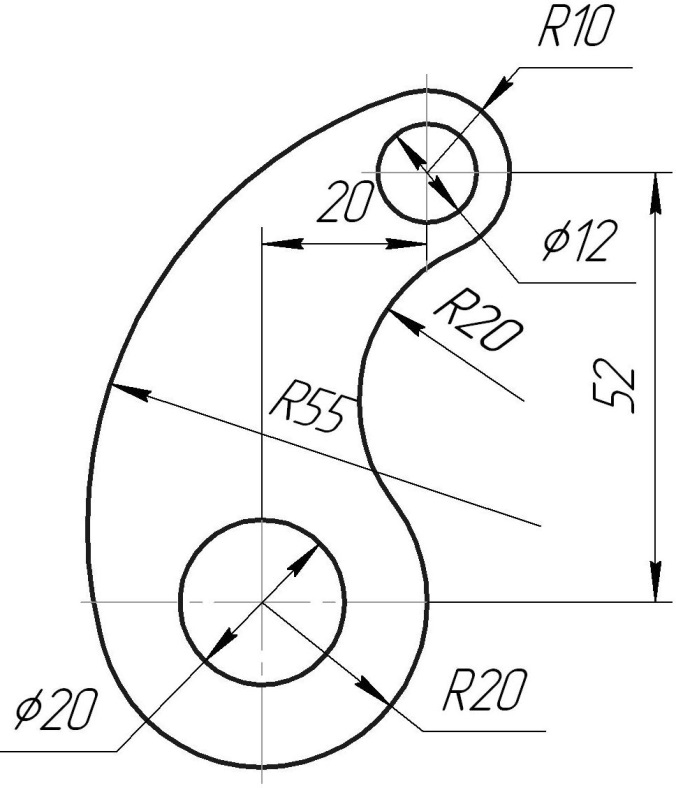
Рисунок 35 - Очертание детали

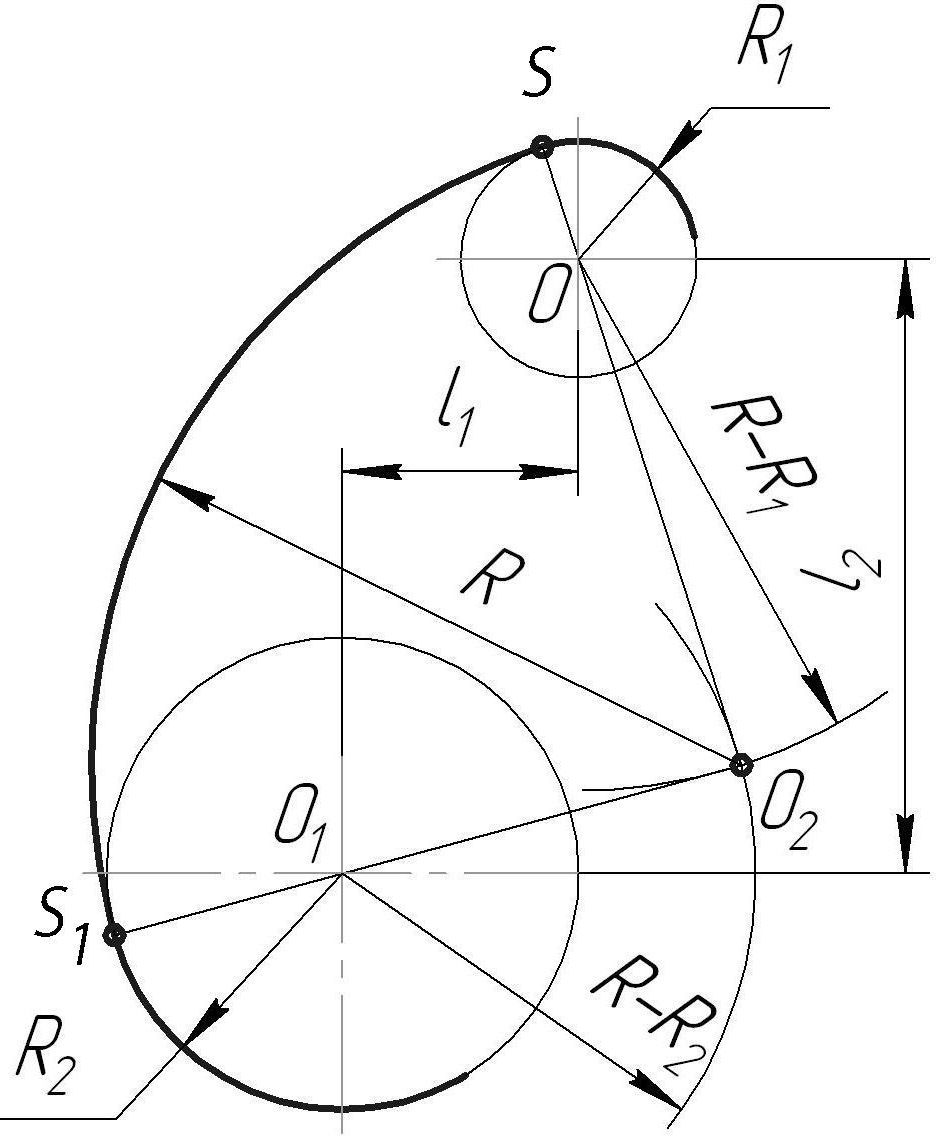
а) б)

Рисунок 36 - Построение внутреннего и внешнего сопряжений

Построение внешнего сопряжения показано на рисунке 36б. По заданным расстояниям между центрами l₁ и l₂ на чертеже намечают центры О и О₁, из которых описывают сопрягаемые дуги радиусов R₁ и R₂. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R₁ и сопрягающей R, а из центра О₁ - радиусом, равным сумме радиусов сопрягаемой R₂ и сопрягающей R. Вспомогательные дуги пересекутся в точке О₂, которая будет искомым центром сопрягающей дуги.

Для нахождения точек сопряжения центры дуг соединяют прямыми линиями ОО₂ и О₁О₂. Эти две прямые пересекают сопрягаемые дуги в точках сопряжения S и S₁. Из центра О₂ радиусом R проводят сопрягающую дугу, ограничивая ее точками сопряжения S и S₁.

На рисунках 37а и 37б показаны очертания технической детали с применением смешанного сопряжения двух дуг окружностей. На рисунке 38 наглядно изображено выполнение смешанного сопряжения дуг окружностей данной детали на чертеже.

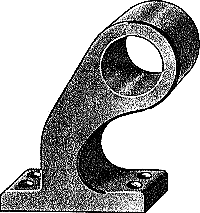
а) б)

Рисунок 37 - Очертание контура детали

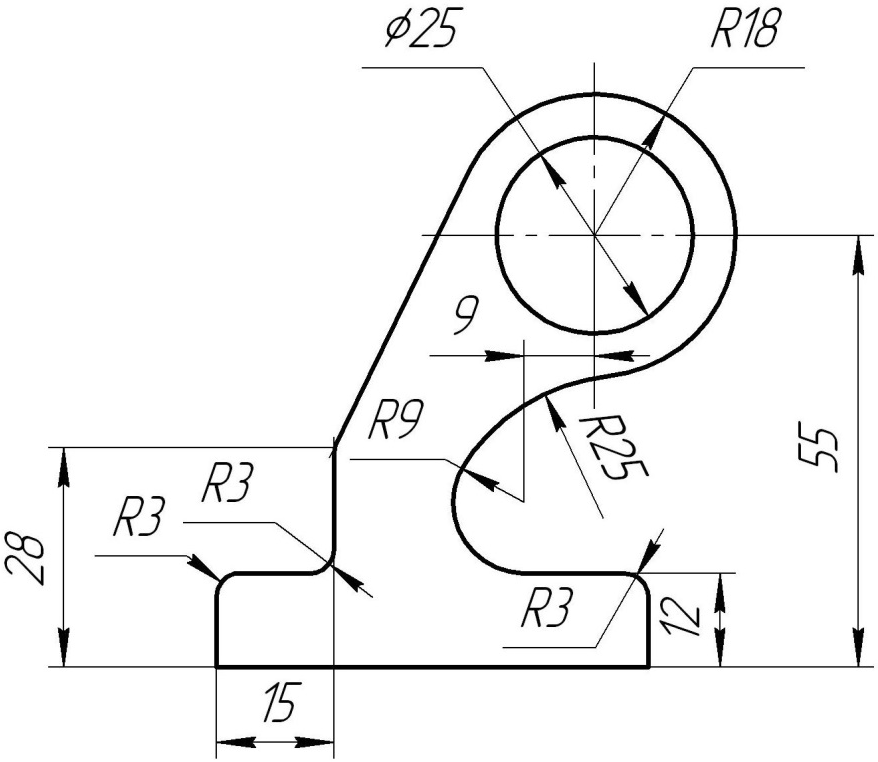
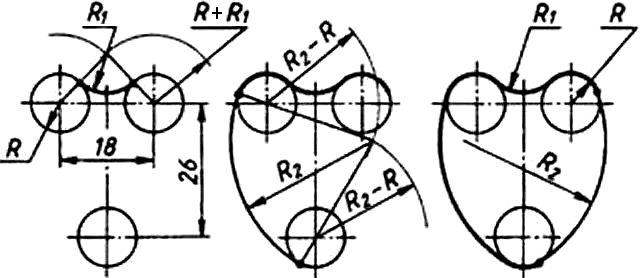
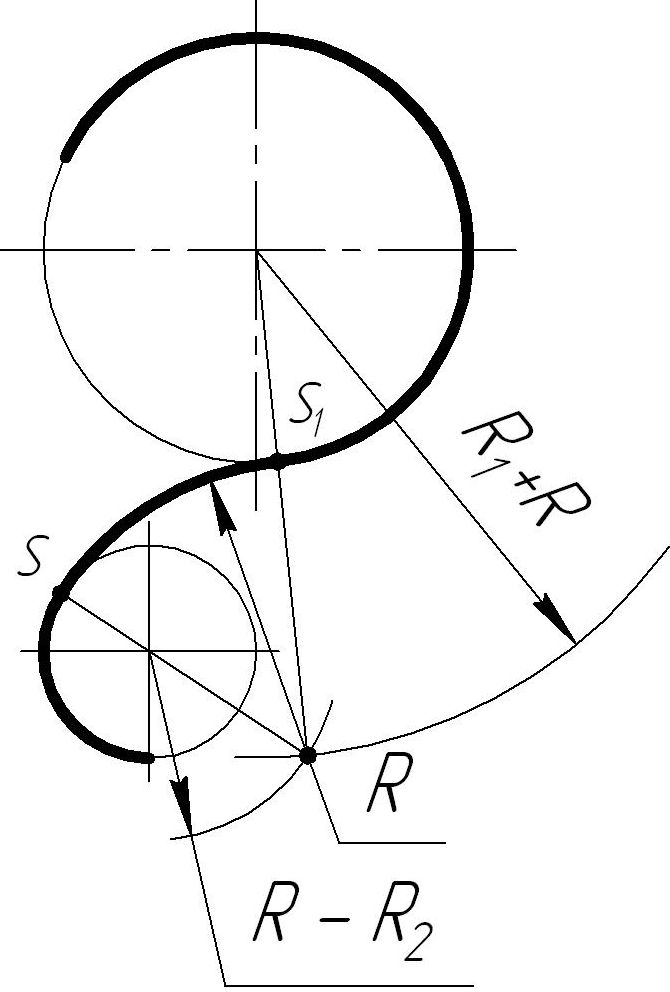На рисунке 39 наглядно показан пример построения фронтальной проекции формы (Рис. 39а), имеющей плавные переходы одной поверхности в другую.

Алгоритм выполнения (Рис. 39б):

1). Проведем осевые и центровые (вертикальные и горизонтальные) линии. На них найдем центры и проведем три дуги радиусом R.

Рисунок 38 - Смешанное сопряжение

2). Найдем центр сопряжения двух верхних окружностей как точку пересечения вспомогательных дуг радиусами, равными сумме радиусов заданной окружности (R) и сопряжения (R₁), то есть R + R₁.

3). Найдем точки внешнего сопряжения. Это точки пересечения заданных окружностей с прямыми, которые соединяют центр

сопряжения с центрами окружностей.

4). Построим сопряжения двух окружностей дугой заданного радиуса сопряжения R₂. Сначала найдем центр внутреннего сопряжения с помощью пересечения дуг вспомогательных окружностей, радиусы которых равны разности радиуса сопряжения R₂ и радиуса окружности R, то есть R₂ - R.

5). Точки сопряжения получаются на пересечении окружности с продолжением линии, соединяющей центр сопряжения с центром окружности. Из центра сопряжения проведем дугу радиусом R₂.

6). Аналогичные построения выполним с другой стороны от оси симметрии.

а) б)

Рисунок 39 - Сопряжение трех дуг окружностей

1.13. Сопряжение двух неконцентрических окружностей

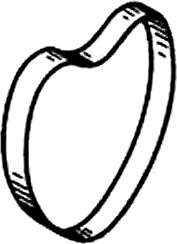
На рисунке 40 изображен крюк. Контур очертания его содержит соединения и переходы неконцентрических окружностей.

Рассмотрим еще раз этапы построения на чертежах подобных сопряжений (Рис. 41):

1). Из центра О₁ заданной окружности проводим вспомогательную дугу радиусом R_С – R₁.

2). Из центра О₂ второй заданной окружности проводим вспомогательную дугу радиусом R₂ + R_С.

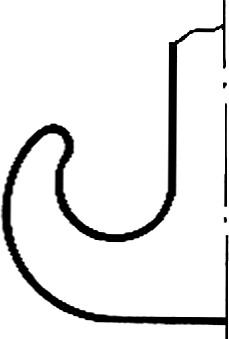
Рисунок 40 -

Очертание крюка

3). Пересечение вспомогательных дуг определяет положение искомого центра сопряжения О_С.

4). Точки сопряжения лежат в местах пересечения линий центров О₂О_С и О₁О_С с заданными окружностями.

5). Точки сопряжения соединяем дугой заданного радиуса сопряжения R_С.

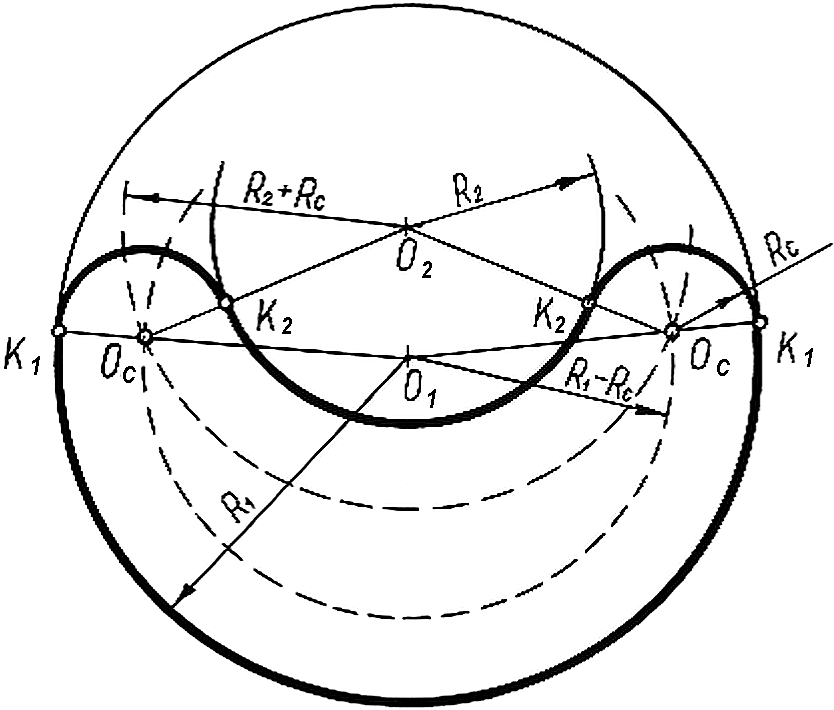
Рисунок 41 - Сопряжение неконцентрических окружностей

Домашнее задание:

На основе данного материала письменно ответьте на следующие вопросы:

1. Что называется сопряжением?

2. Как определяется точка сопряжения?

3. Каков порядок решения примеров на сопряжение?

4. Что служит промежуточной линией при сопряжении? Как строится внутреннее сопряжение двух окружностей?

5. Что такое смешанное сопряжение?

6. Способы деления окружности на равные части.

7. Какова последовательность выполнения чертежа детали, в очертании которой имеется сопряжение?

Форма отчетности: прислать скан выполненной работы на электронный адрес: nesterova.911@yandex.ru