Учебная дисциплина Техническое черчение

Учебная дисциплина Техническое черчение

Гр№ 11

Занятие № 13

Дата: 30 сентября 2021г

Тема занятия «Лекальные кривые»

Цели работы: изучить материал, циркульными и лекальными кривыми.

Изучение материала:

ЦИРКУЛЬНЫЕ КРИВЫЕ

В технике часто применяются различные кривые, которые мо- гут быть замкнутыми и незамкнутыми. Некоторые из них строят с помощью циркуля, и поэтому они называются ци ркульными или ко робовыми кривыми – это овал, овоид, завиток и др. Для по- строения эллипса, параболы, гиперболы, циклоиды, синусоиды и т.п., необходимо сначала определить несколько точек, которые им принадлежат, а затем соединить эти точки с помощью лекала. Такие кривые называются лека льными. Рассмотрим построение некоторых кривых.

Циркульные кривые состоят из сопряжений дуг окружностей и соединяются друг с другом с помощью циркуля.

1.1. Овал

Ова л -это замкнутая кривая линия, которая состоит из дуг сопрягающихся окружностей. Овал имеет две оси симметрии: АВ

- большая ось, CD - малая ось (рис.1).

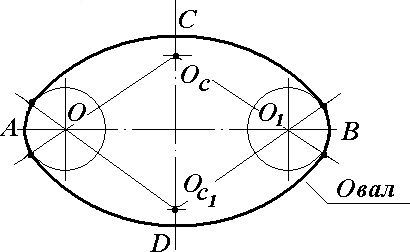
Рис.1.

Задача. Построить овал с осями АВ и СD.

I) Даны две взаимно перпендикулярные оси овала АВ и CD (рис. 2).

2) С центром в точке О проводим дугу радиусом ОА, получаем точку К, соединяем точки А и С.

3) С центром в точке С проводим дугу радиусом СК, получаем точку L . Отрезок АL делим на две равные части, получаем точки O₁ и O_c.

4) Симметрично точкам O₁ и O_c расположены точки O₁' и O_с'. Со- единяем точки O_c и O₁', O_c' и O₁', O_c' и O₁.

5) С центром в точке O₁ проводим дугу радиусом O₁А. С центром в точке O₁ проводим дугу радиусом O₁'В.

6) С центром в точке O_c проводим дугу радиусом O_cС. С центром в точке O_c' проводим дугу радиусом O_c'D.

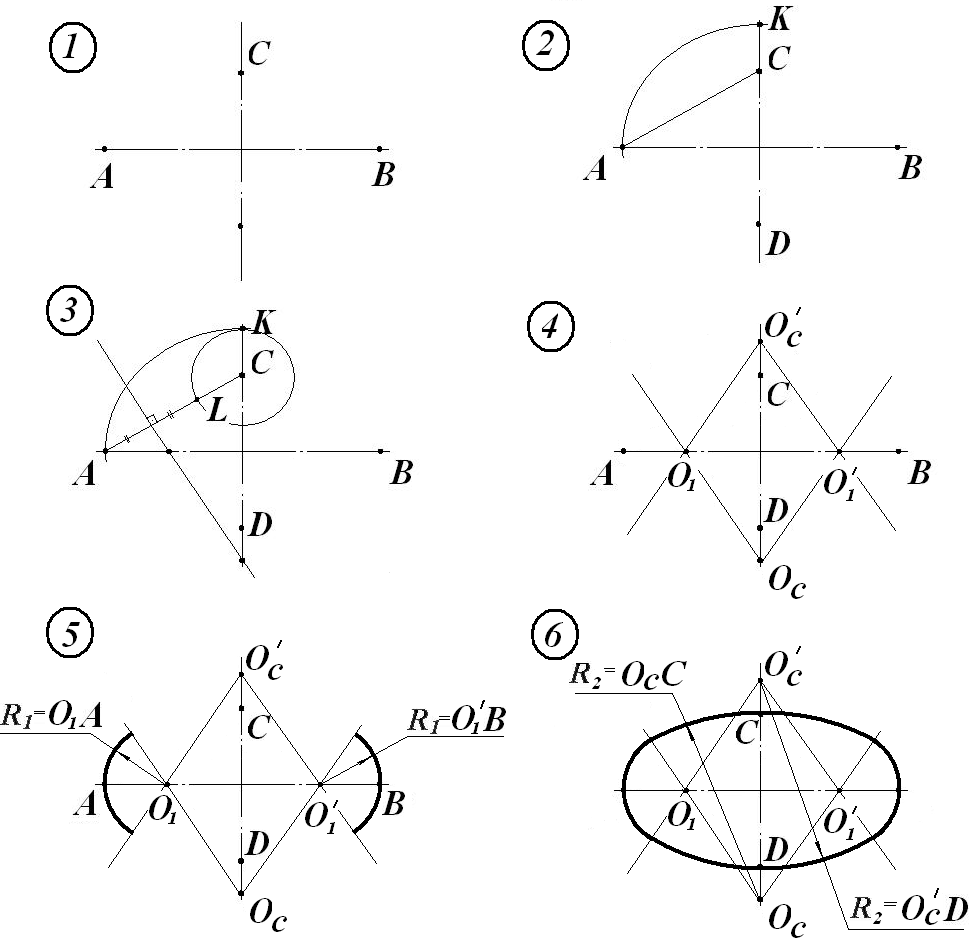
Рис. 2.

1.2. Овоид

Ово ид - замкнутая коробовая кривая, которая имеет только одну ось симметрии.

Задача. Построить овал, который имеет одну ось симметрии.

I) Даны две взаимно перпендикулярные оси овала АВ и CD (рис. 3).

2) С центром в точке О проводим дугу радиусом ОА. Проводим прямые АD и ВD.

3) С центрами в точках А и В проводим дуги радиусом R₁=2R и получаем точки E и F.

4) С центром в точке D проводим дугу EKF радиусом R₂=DE=DF. СК - ось симметрии овала (овоида).

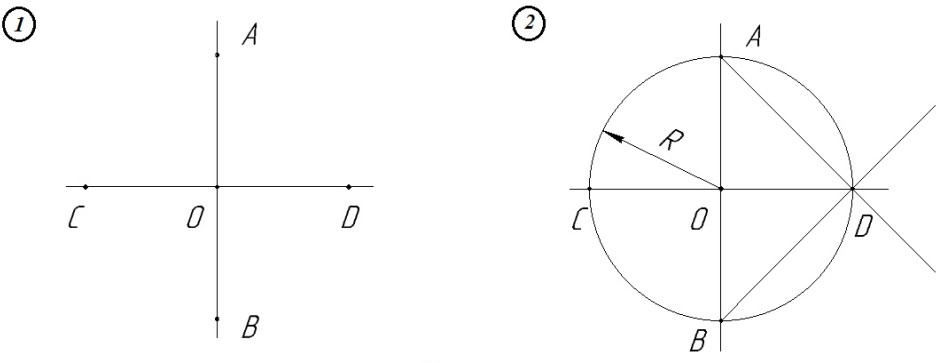
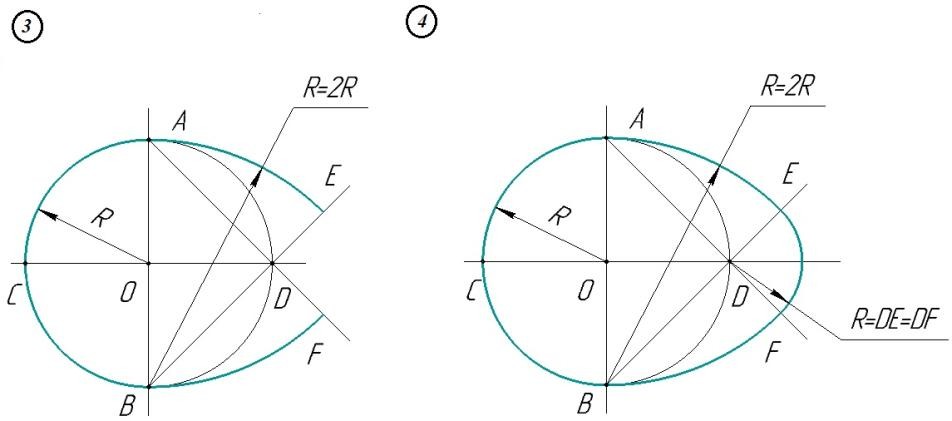
Рис. 3.

1.3. Завиток

Завито к - это плоская спиральная кривая.

Построение завитков выполняют при вычерчивании таких де- талей, как пружины и спиральные направляющие.

Построение завитков выполняется из двух, трех и более цен- тров и зависит от формы и размеров “глазка”, который может быть окружностью, правильным треугольником, шестиугольником и т.п.

Задача. Построить завиток, который имеет три центра.

1) Дан правильный треугольник АВС (рис. 4).

2) Продолжим стороны треугольника в одном направлении, например по движению часовой стрелки.

3) С центром в точке В в направлении против часовой стрелки проводим дугу радиусом R=BA.

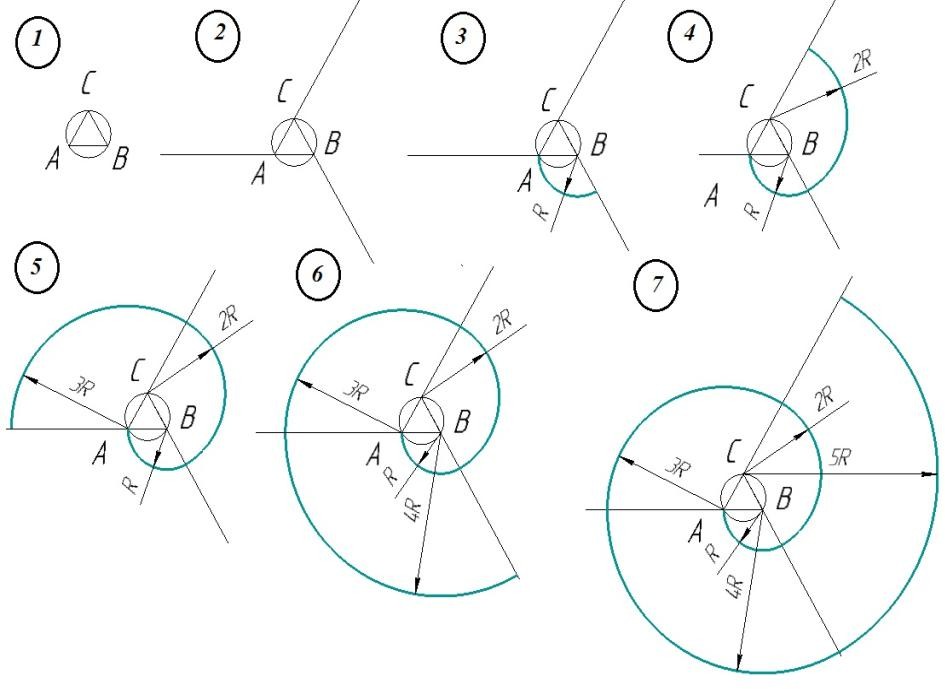
Рис. 4.

4) С центром в точке C в направлении против часовой стрелки проводим дугу радиусом 2R.

5) С центром в точке A в направлении против часовой стрелки проводим дугу радиусом 3R.

6) С центром в точке B в направлении против часовой стрелки проводим дугу радиусом 4R.

7) С центром в точке C в направлении против часовой стрелки проводим дугу радиусом 5R.

Аналогично построение можно продолжать до необходимого числа витков.

На рисунке 5 показано построение завитка из пяти центров в направлении по движению часовой стрелки.

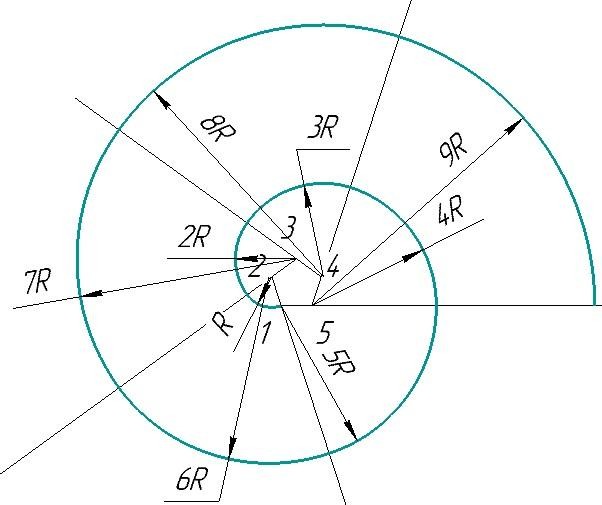
Рис. 5.

1. ЛЕКАЛЬНЫЕ КРИВЫЕ

При выполнении чертежей часто необходимо чертить кривые, которые нельзя построить с помощью циркуля. Такие кривые строят обычно по ряду принадлежащих им точек, которые затем соединяют плавной линией при помощи лекал.

Лека льная крива я - это плавная кривая линия, образован- ная точками, которые соединяют с помощью лекал. Лекальные кривые располагаются в одной плоскости и поэтому называются плоскими. Лекальные кривые широко применяются в машино- строении для очертания различных технических деталей, напри- мер: кронштейнов, ребер жесткости, кулачков, зубчатых колес, фасонного инструмента и т.п.

Лекальные кривые - это эллипс, парабола, гипербола, цик- лоида, эпициклоида, эвольвента, синусоида, спираль Архимеда и др.

Рассмотрим построение эллипса, параболы, гиперболы.

1.1. Эллипс

Э ллипс – это замкнутая плавная кривая линия (рис. 6). АВ - большая ось эллипса, СD – малая ось эллипса. F₁ и F₂ – фокусы эллипса. Свойство эллипса: сумма расстояний от любой точки эл- липса до фокусов есть величина постоянная, которая равна длине большой оси эллипса (АВ):

АС + СВ= Е F₁ + Е F₂ = АВ

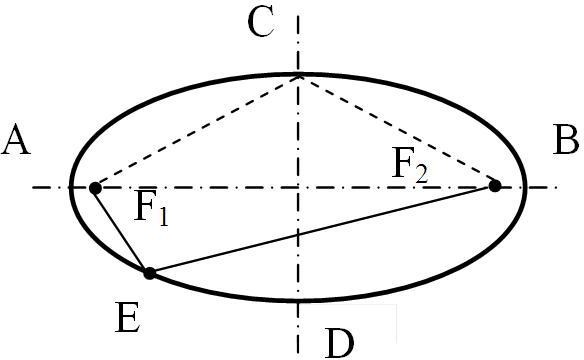
Рис. 6.

Задача. Построить эллипс с осями АВ и СD.

1) Даны две взаимно перпендикулярные оси эллипса АВ и СD

(рис. 7).

2) С центром в точке О проводим окружности радиусами AВ и

ОС.

3) Эти окружности разделим на двенадцать равных частей.

4) Из точек деления большой окружности проводим линии,

параллельные оси СD.

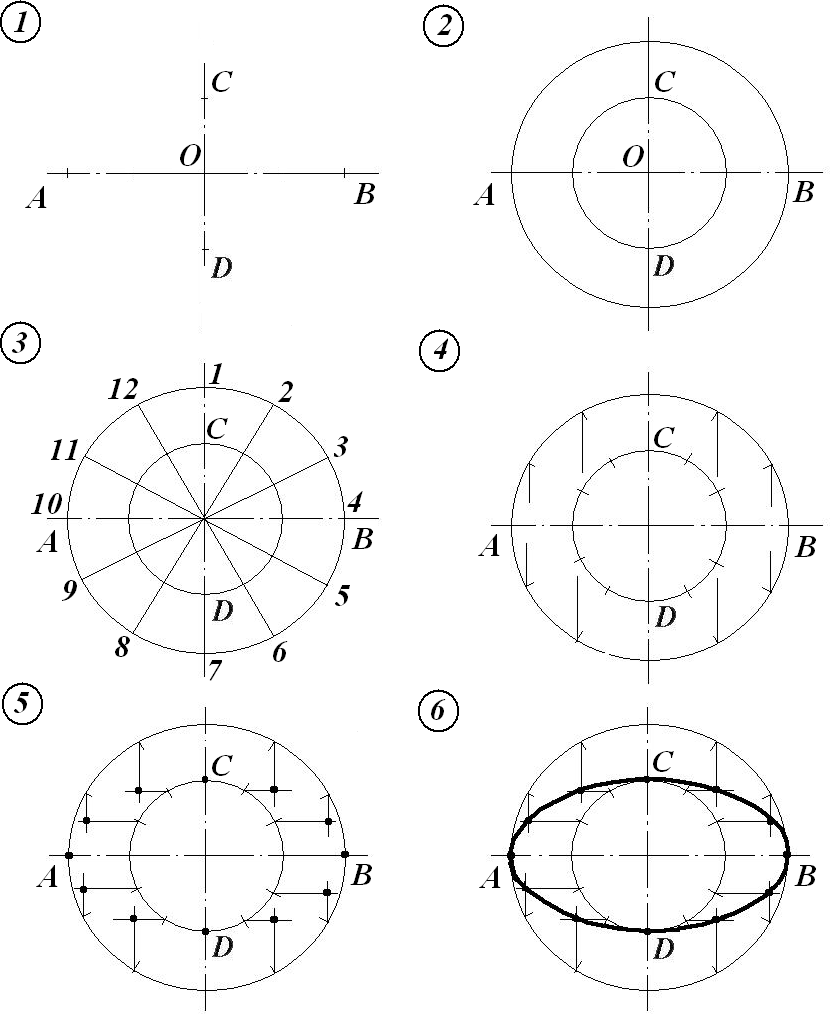
Рис. 7.

5) Из точек деления малой окружности проводим линии, па- раллельные оси АВ. Точки пересечения вертикальных к горизон- тальных линий - это точки эллипса.

6) Соединяем полученные точки плавной кривой с помощью лекала.

2.3. Парабола

Пара бола - это незамкнутая кривая, которая состоит из то- чек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой (директрисы) (рис.8).

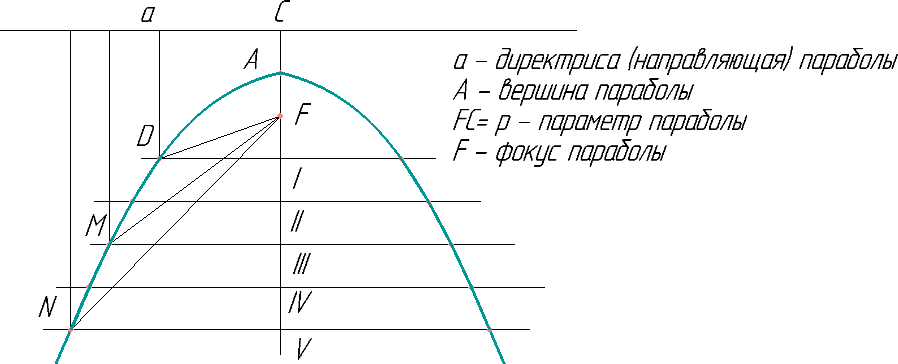
Рис. 8.

Задача. Построить параболу по параметру р=FC=20 мм (рис.

9).

1) Через точку С проводим прямую а - директрису параболы.

2) Чертим серединный перпендикуляр к отрезку СF и отмеча-

ем точку А - вершину параболы.

3) Через точки С и F чертим вертикальную прямую - ось сим- метрии параболы. На оси симметрии вниз от точки F откладывает несколько произвольных точек I, II, III, IV, V.

4) Через точки I,, II, III, IV, V чертим прямые, перпендикуляр- ные оси параболы СF. С центром в точке F чертим дугу радиусом IС и отмечаем точки пересечения с прямой, проведенной через точку I на оси. С центром в точке F чертим дугу радиусом IIС и отмечаем точки пересечения с прямой, проведенной через точку II на оси. Аналогично получаем другие точки параболы.

5) Соединяем точки параболы плавной кривой с помощью ле- кала.

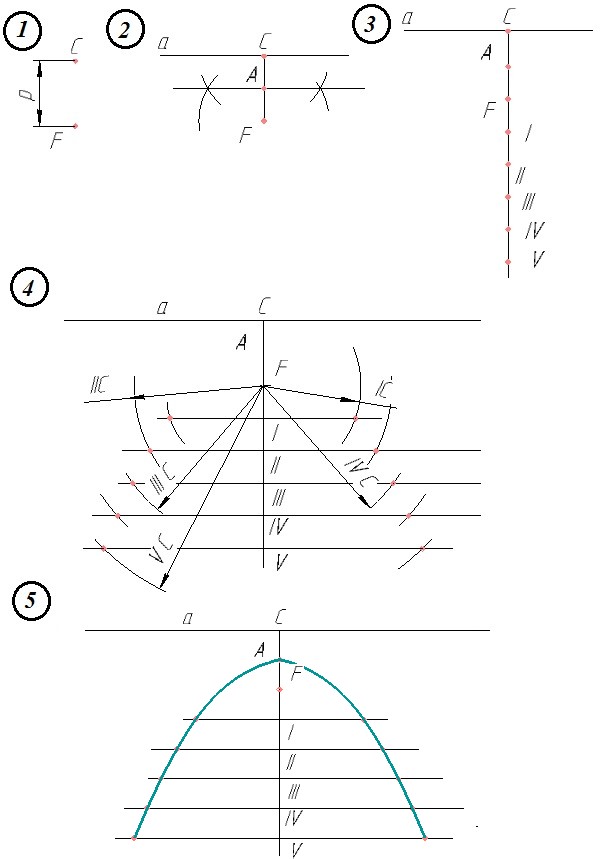
Рис. 9.

Задача. Построить параболу по вершине, оси и точке (рис. 10).

1) Дана прямая а - ось параболы, точки В - вершина параболы и А -точка параболы.

2) Через точку В чертим горизонтальную прямую, а через точ- ку А -вертикальную. Получаем точку пересечения - С. Делим от- резки ВС и АС на произвольное число равных частей, например 5

(используем универсальный метод деления отрезка на равные части).

3) Соединим точки деления 1,2,3,4,5 на отрезке АС с вершиной параболы - точкой В.

4) Через точки деления 1,2,3,4,5 на отрезке ВС проводим пря- мые, параллельные АС, до пересечения с соответствующими на- клонными прямыми и получаем точки параболы I, II, III, IV, V.

5) Находим симметричные относительно оси а точки параболы и соединяем их плавной кривой с помощью лекала.

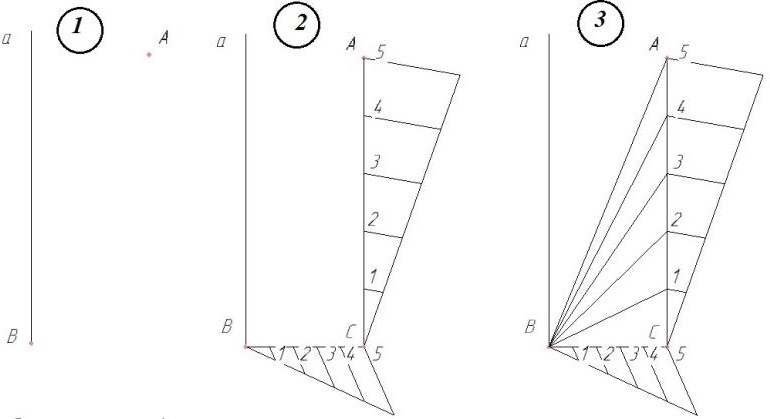
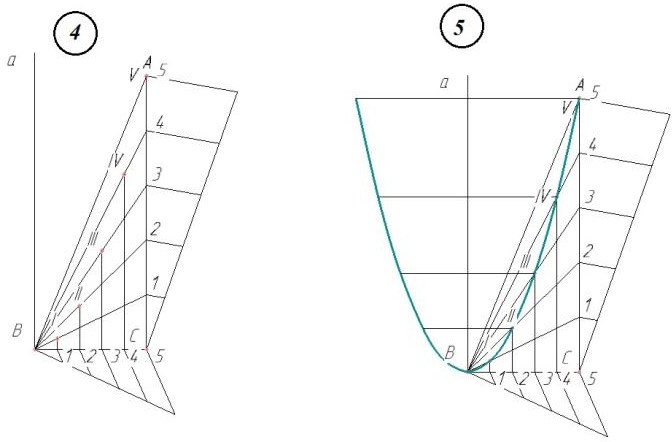
Рис. 10.

2.3. Гипербола

Гипе рбола(рис. 11) - это незамкнутая плоская кривая, у ко- торой разность расстояний от каждой ее точки до двух данных точек F₁ и F₂ (фокусы гиперболы), есть величина постоянная и равная расстоянию между ее вершинами A и B, например F₂N- F₁N=AB. У гиперболы две оси симметрии - действительная АВ и мнимая CD.

Две прямые m и n, которые проходят через центр О гипербо- лы и касаются ее ветвей в бесконечности, называются асим- пто тами.

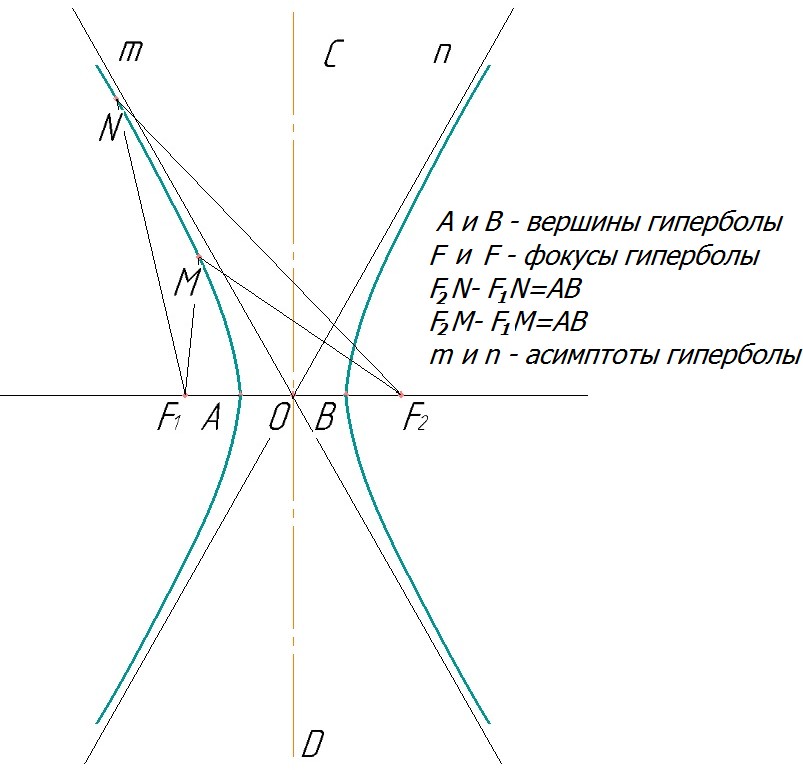
Рис. 11.

Задача. Построить гиперболу по заданным вершинам A и B, и фокусам F₁ и F₂ (рис.12).

1) Даны два фокуса гиперболы - F₁, F₂ и вершины A и B.

2) На действительной оси АВ слева от фокуса F₁ отмечаем произвольные точки I, II, III, IV .

3) Из фокусов F₁ и F₂ проводим дуги окружностей сначала ра- диусом А1, затем B1 до взаимного пересечения в точке М.

4) Выполним взаимное пересечение всех пар дуг соответст- вующими радиусами, получим точки N, L, K. Относительно оси АВ построим симметричные им точки. Все точки принадлежат левой ветви гиперболы.

5)
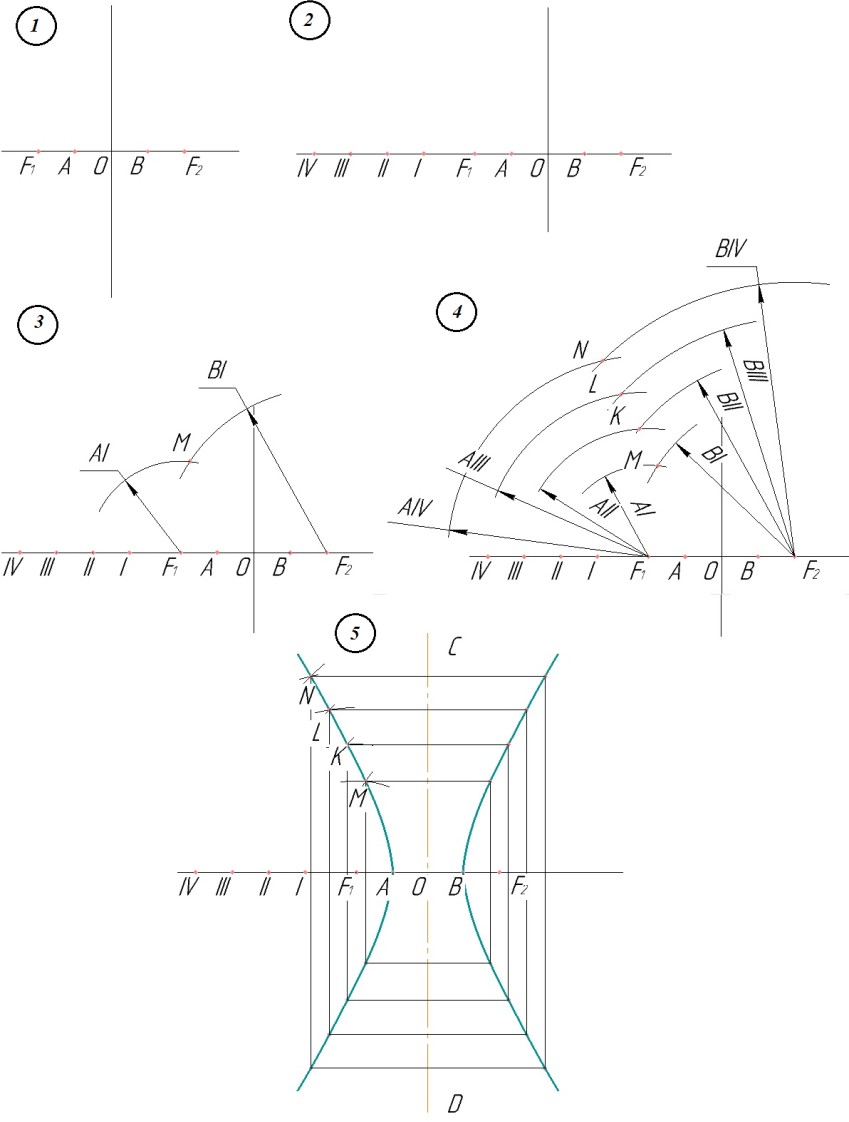
Точки правой ветви будут симметричны построенным точ- кам относительно мнимой оси CD.

Рис. 12.

Задача. Построить гиперболу по асимптотам и точке (рис.

13.).

1) Даны асимптоты m и n и произвольная точка A параболы.

2) Через точку A проводим произвольную секущую а и отме- чаем точки пересечения этой прямой с асимптотами - точки В и С. От точки С отложим отрезок, равный отрезку АВ и получим точку гиперболы - D.

Через точку A проводим произвольную секущую l и отмечаем точки пересечения этой прямой с асимптотами - точки L и N От точки N отложим отрезок, равный отрезку АL и получим точку ги- перболы - E.

3) Таким же способом находим точки гиперболы F и G.

4) Соединяем точки D, E, F и G плавной кривой с помощью ле- кала.

5)
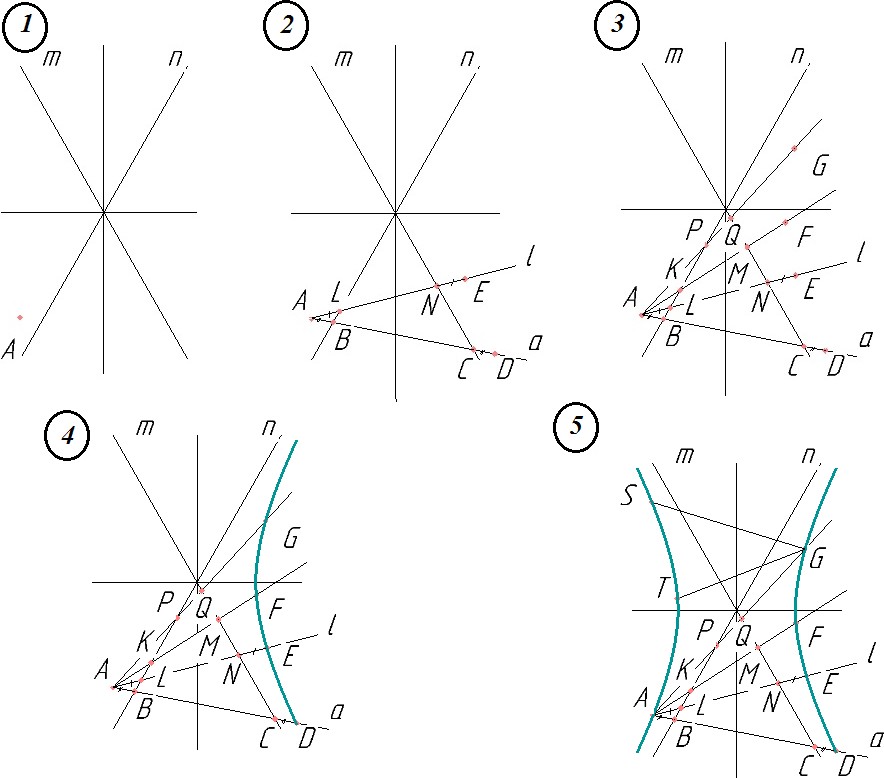
Таким же способом находим точки гиперболы слева от мнимой оси гиперболы S и T. Соединяем точки S, T и A плавной кривой с помощью лекала.

Рис. 13.

Структурно-логическая схема темы циркульные и лекальные кривые представлена на рис.14.

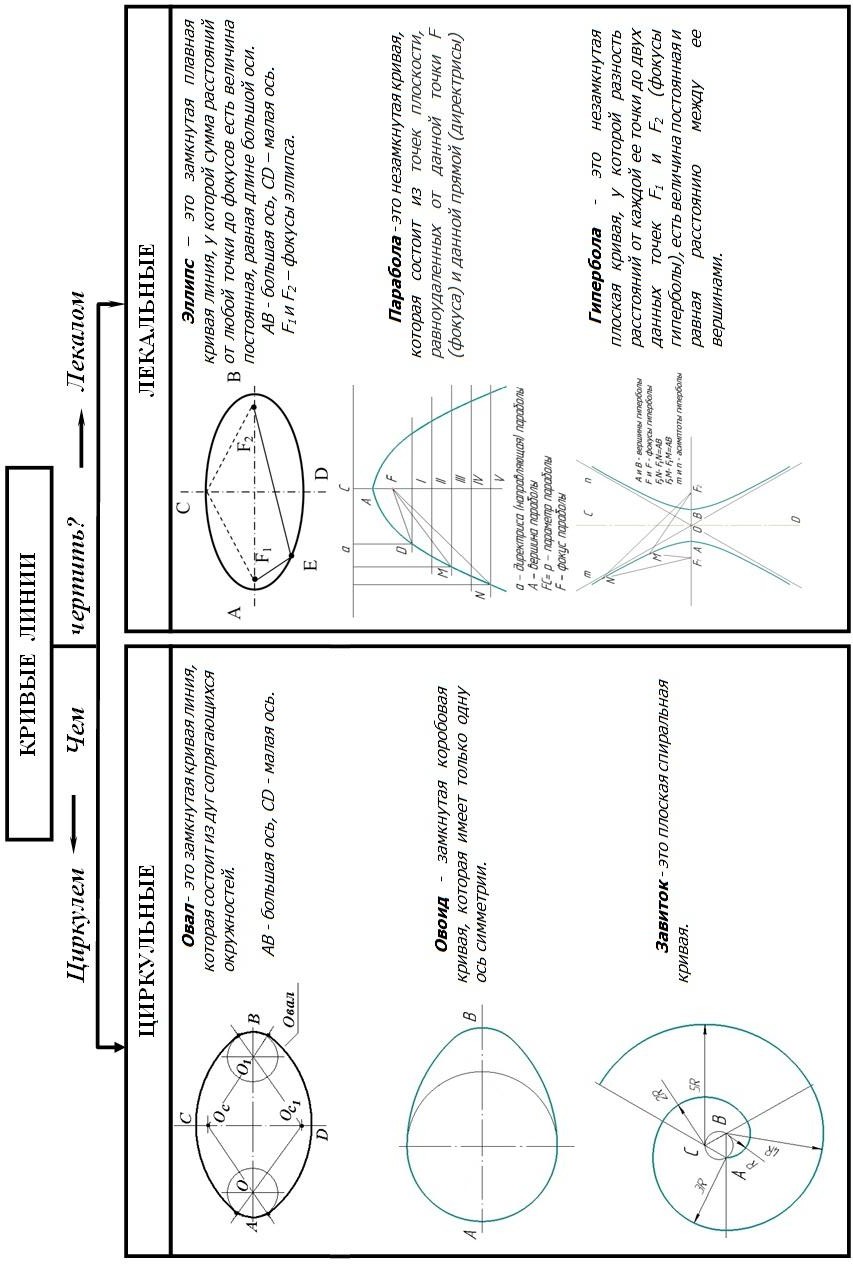
Рис. 14. Структурно-логическая схема темы циркульные и ле- кальные кривые.

Домашнее задание:

На основе данного материала письменно ответьте на следующие вопросы:

I. Что такое овал?

2. Какие инструменты вы используете для построения овала?

3. Что такое эллипс?

4. Какое свойство эллипса вы знаете?

5. Какие инструменты вы используете для построения эллипса?

6. Какая кривая называется овоидом?

7. Как называется плоская спиральная кривая?

8. Какая кривая называется параболой?

9. Какая кривая называется гиперболой?

10. Какие инструменты вы используете для построения параболы и гиперболы?

Форма отчетности: прислать скан выполненной работы на электронный адрес: nesterova.911@yandex.ru