
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Межрегиональный центр переподготовки специалистов
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Экзаме по дисциплине
«Методы оптимальных решений»
Выполнил: Шмидт И.А.
Группа: ФКТ - 21
Вариант:1
Проверил: ___________________
Новосибирск, 2013 г
1.Решить графически задачу линейного программирования:
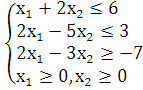
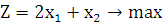
Решение
Запишем исходную задачу в стандартной форме:
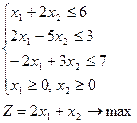
Имеем 3 уравнения, определяющих три граничные прямые:
х1 + 2х2 = 6, (1)
2х1 – 5х2 = 3, (2)
-2х1 + 3х2 = 7, (3)
Градиент функции Z:
grad Z = (2, 1).
Строим область допустимых решений и находим точку максимума.
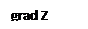
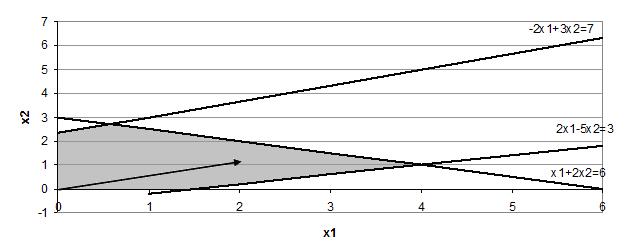
Найденная точка максимума находится на пересечении прямых (2) и (1).
Координаты этой точки:
Х* = (4, 1).
Z* = 2*4 + 1 = 9.
Ответ: Х* = (4, 1), Z* = 9.
1. Сельскохозяйственное предприятие планирует посадить некоторую сельскохозяйственную культуру двух сортов. Посевная площадь 1000 га. Сорта отличаются друг от друга требованиями к влаге во время вегетационного периода. Проанализировав погодные условия, выделены 4 состояния погоды (S1, S2, S3, S4), отличающиеся режимом осадков. Средняя урожайность (ц/га) каждого сорта на всем участке для каждого состояния погоды приведена в таблице:
| S1 | S2 | S3 | S4 | |
| Сорт 1 | ||||
| Сорт 2 |
Возможные варианты посева:
А1) сорт 1 посадить на 100% площади;
А2) сорт 1 посадить на 75% площади, сорт 2 посадить на 25% площади;
А3) сорт 1 посадить на 50% площади, сорт 2 посадить на 50% площади;
А4) сорт 1 посадить на 25% площади, сорт 2 посадить на 75% площади;
А5) сорт 2 посадить на 100% площади;
Определить оптимальную стратегию с помощью критериев недостаточного основания Лапласа, максиминного критерия Вальда, критерия минимаксного риска Сэвиджа, пессимизма-оптимизма Гурвица (коэффициент пессимизма взять равным 0,4).
Решение
Рассчитаем элементы матрицы полезности:
| S1 | S2 | S3 | S4 | |
| А1 | ||||
| А2 | ||||
| А3 | ||||
| А4 | ||||
| А5 |
Элементы данной матрицы – сбор урожая (ц), при заданных вариантах посева и погодных условиях.
1. Критерий Лапласа
В основе этого критерия лежит "принцип недостаточного основания".
Если принять, что любой из вариантов погодных условий не более вероятен, чем другие, то вероятности различных вариантов погодных условий можно принять равными и задача сводится к поиску варианта, дающего
А = max 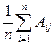
А1 = (26000 + 32000 + 34000 + 40000)/4 = 33000,
А2 = (29250 + 33000 + 33250 + 36750)/4 = 33063,
А3 = (32500 + 34000 + 32500 + 33500)/4 = 33125,
А4 = (35750 + 35000 + 31750 + 30250)/4 = 33188,
А5 = (39000 + 36000 + 31000 + 27000)/4 = 33250.
Выбор максимального значения обнаруживает оптимальность выбора варианта А5: сорт 2 посадить на 100% площади.
2. Критерий Вальда
Критерий Вальда обеспечивает выбор осторожной, пессимистической стратегии в той или иной деятельности и его суждения близки к тем суждениям, которые мы использовали в теории игр для поиска седловой точки в пространстве чистых стратегий: для каждого решения Xi выбирается самая худшая ситуация (наименьшее из Аij) и среди них отыскивается гарантированный максимальный эффект
А = 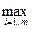
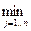 Aij
Aij
A = max(26000, 29250, 32500, 30250, 27000) = 32500, т.е. по этому критерию следует выбрать вариант А3: сорт 1 посадить на 50% площади, сорт 2 посадить на 50% площади.
3. Критерий Сэвиджа
Суть этого критерия заключается в нахождении минимального риска. При выборе решения по этому критерию сначала матрице функции полезности (эффективности) сопоставляется матрица сожалений
Dij = Aij – 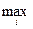 (Aij)
(Aij)
элементы которой отражают убытки от ошибочного действия, т.е. выгоду, упущенную в результате принятия i-го решения в j-м состоянии. Затем по матрице D выбирается решение по пессимистическому критерию Вальда, дающее наименьшее значение максимального сожаления.
Отыскиваем матрицу D, вычитая 39000 из первого столбца матрицы полезности, 36000 из второго, 34000 из третьего, 40000 из четвертого.
| S1 | S2 | S3 | S4 | |
| А1 | -13000 | -4000 | ||
| А2 | -9750 | -3000 | -750 | -3250 |
| А3 | -6500 | -2000 | -1500 | -6500 |
| А4 | -3250 | -1000 | -2250 | -9750 |
| А5 | -3000 | -13000 |
Наибольшее значение среди минимальных элементов строк здесь равно max(-13000, -9750, -6500, -9750, -13000)= -6500. По этому критерию следует выбрать вариант А3: сорт 1 посадить на 50% площади, сорт 2 посадить на 50% площади, при этом потери урожая не превысят 6500 ц.
4. Критерий Гурвица
Оптимальным решением будет то, для которого окажется максимальным показатель G :
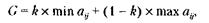
где аij – выигрыш, соответствующий i-му решению при j-м варианте обстановки;
k – коэффициент пессимизма = 0,4.
| k = 0,4 | |
| А1 | 0,4*26000 + 0,6*40000 = 34400 |
| А2 | 0,4*29250 + 0,6*36750 = 33750 |
| А3 | 0,4*32500 + 0,6*34000 = 33400 |
| А4 | 0,4*30250 + 0,6*35750 = 33550 |
| А5 | 0,4*27000 + 0,6*39000 = 34200 |
При k = 0,4 следует выбрать вариант А1: сорт 1 посадить на 100% площади и ожидать урожай порядка 34400 ц.
Таким образом, различные критерии приводят к различным выводам:
1) по критерию Лапласа сорт 2 посадить на 100% площади,
2) по критерию Вальда и критерию Сэвиджа - сорт 1 посадить на 50% площади, сорт 2 посадить на 50% площади,
3) по критерию Гурвица - сорт 1 посадить на 100% площади.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|