Двойственные задачи линейного программирования

Двойственные задачи линейного программирования

Будем называть задачу вида

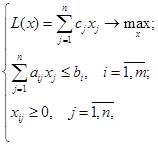
где 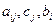- действительные числа, 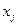-компоненты вектора переменных размерности 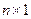, прямой задачей линейного программирования (ЗЛП).

В соответствие ей можно поставить другую задачу:

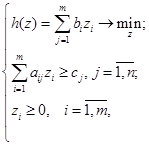
где 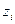- компоненты вектора двойственных переменных размерности .

Теорема 1. Для любого решения прямой ЗЛП и любого решения двойственной ЗЛП 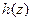справедливо соотношение: .

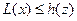Теорема 2. Пусть 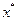- оптимальное решение прямой ЗЛП, 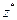- оптимальное решение двойственной ЗЛП, тогда справедливо равенство: .

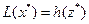Теорема 3. Пусть 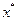- оптимальное решение прямой ЗЛП, 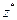- оптимальное решение двойственной ЗЛП, тогда справедливы следующие равенства:

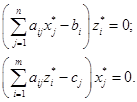
Пример. Дана прямая ЗЛП:

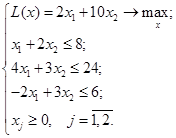
Ей соответствует двойственная ЗЛП

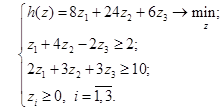
Решив задачи, найдём:

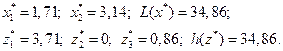
Проверка показывает справедливость теорем 2 и 3; при этом оптимальному значению 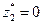в прямой ЗЛП соответствует неактивное ограничение (при решении задачи в Excel с помощью процедуры «Поиск решения» ограничение имеет статус несвязанного).

Задание. Для предложенной ЗЛП (прямой или двойственной) записать парную ей (двойственную или прямую). Найти с помощью табличного процессора Excel оптимальные решения задач, убедиться в справедливости теорем 2 и 3.