Хелпикс

Главная

Контакты

Случайная статья



Законы умножения.

Стр 1 из 2Следующая ⇒


 

Тема. Умножение. Законы умножения. Распределительный закон. (Запимать число и тему)

Цель. Формирование умений и навыков умножения натуральных чисел и законов умножения.

Посмотреть видео урок:

https://youtu.be/qyIzYJT4-ZI

Умножение.

Умножить натуральное число 3 на натуральное число 4 – значит найти сумму трех слагаемых, каждое из которых 4.

3 × 4 = 4 + 4 + 4 + 4 = 12.

Числа 3 и 4 называют множителями, 12 – произведение.

Запомните: Умножить число а на натуральное число b — значит найти сумму а одинаковых слагаемых, каждое из которых равно b.

                    

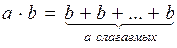
Умножение — это арифметическое действие второй ступени.

Как называются компоненты при умножении? (Числа, которые нужно умножить, называ­ются множителями. Число, получаемое в результате умножения, называется произведением.).

Понятно, что если один из множителей равен 1, то произведение равно второму множителю: а × 1 = а,  1 × а = а.

Если один из множителей равен 0, то произведение равно 0:

                           а × 0 = 0, 0 × а = 0.

Пример 1.(Записать) Запишите произведение в виде суммы и найдите значение:

1) 5 × 3 = 3 + 3 + 3 + 3 + 3 = 15 (Записали сумму пяти слагаемых, каждое из которых равно 3);

2) 3 × 5 = 5 + 5 + 5 = 15       (Записали сумму трех слагаемых, каждое из которых равно 5);

3) 3 × 1 = 1 + 1 + 1 = 3       (Записали сумму трех слагаемых, каждое из которых равно 1);

4) 1 × 7 = 7                        (Записали сумму одного слагаемого, которое равно 7).

 

Законы умножения.

Изменится ли произведение, если поменять местами множители? Нет.

Такое свойство справедливо для любых чисел а и b. Это — переместительный закон умножения.

Запомните: Переместительный закон умножения.

От перестановки множителей произведение не изменяется. а × b = b × а. (записать)

Вы уже знаете, что результат умножения нескольких множителей не зависит от порядка выполнения умно­жения. Например, чтобы найти произведение чисел 10, 2 и 15, можно сначала перемножить числа 10 и 2, а за­тем их произведение умножить на число 15. Но удобнее сначала перемножить числа 2 и 15, а затем на их произ­ведение умножить число 10. Порядок умножения чисел указывают при помощи скобок. Для рассматриваемого примера получим: (10 × 2) × 15 = 10 × (2 × 15).

    

Такое свойство справедливо для любых чисел а, b и с. Это — сочета-тельный закон умножения.

                      

Запомните:чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего. (а ×b) × с = а × (b × с). (Записать)

Опираясь на переместительный и сочетательный за­коны, можно применять и такой способ группировки множителей: второе число умножить на произведение первого и третьего. Например, для нахождения про­изведения чисел 10, 2 и 15, кроме уже рассмотренных способов, существует третий способ: (10 × 15) × 2.

Переместительный и сочетательный законы умноже­ния справедливы для любого количества множителей. Применяя эти законы, можно значительно упростить вычисления. Рассмотрим примеры.

Пример 2. (Записать) Найдите произведение:

1) 4 × 37 × 25 = (4 × 25) × 37 = 100 × 37 = 3 700;

2) (25 × 5) × (4 × 20) = (25 × 4) × (5 × 20) = 100 × 100 = 10 000.

 

Обратите внимание:

1) вычисляя произведение нескольких чисел, мож­но по-разному переставлять и группировать мно­жители;

2) если выражение в скобках содержит только действие умножения, то в таком выражении скобки можно опустить (не записывать).

Выполнить письменно:

 


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.