Лабораторная 5

Лабораторная 5

1) Задание 4, вариант 26.

Построим график функции, от которой будем вычислять определенный интеграл:

x=0.0:0.01:5;

u=(x.^2+3)./(x.^3+4);

hold on

grid on

plot(x,u)

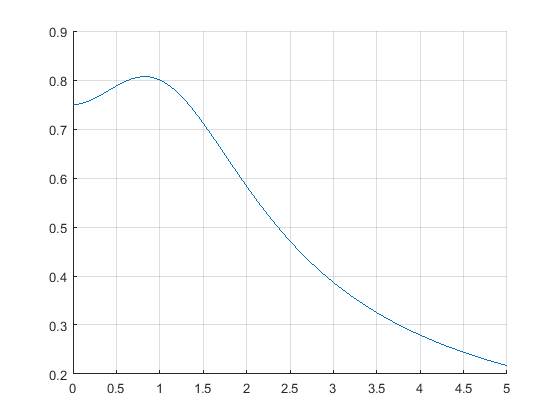
Существует два способа вычислить определенный интеграл: методом Симпсона(через функцию integral) и методом трапеции:

*Методом трапеции вычислим интеграл на промежутке [0,0;0,18]

x=0.0:0.01:1.8;

u=(x.^2+3)./(x.^3+4);

area(u);

hold on

grid on

U1=trapz(x,u)

получим значение

U1 =

1.3668

*Методом Симпсона мы сначала приводим функцию к анонимному виду:

u=@(x) (x.^2+3)./(x.^3+4);

integral(u,0,1.8, 'AbsTol', 15e-4) - здесь мы пишем интегрируемую функцию, пределы интегрирования, а также задаем абсолютную погрешность(0,0015)

получим на выходе

ans =

1.3668

Вывод: оба метода дают одинаковые численные ответы, по удобству метод Симпсона выигрывает, но по методу трапеции при помощи команды area(y) можно построить график и увидеть данный метод в действии.

2) Построим график нелинейной функции:

x=0.4:0.01:0.6;

u=sqrt(x)-cos(sqrt(x));

hold on

grid on

plot(x,u)

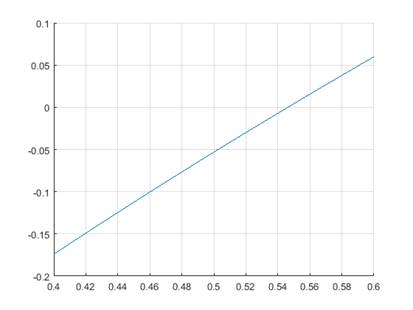
*Вычислим определенный интеграл методом трапеции на интервале [0.4;0.6]

x=0.4:0.01:0.6;

u=sqrt(x)-cos(sqrt(x));

area(u);

hold on

grid on

U1=trapz(x,u)

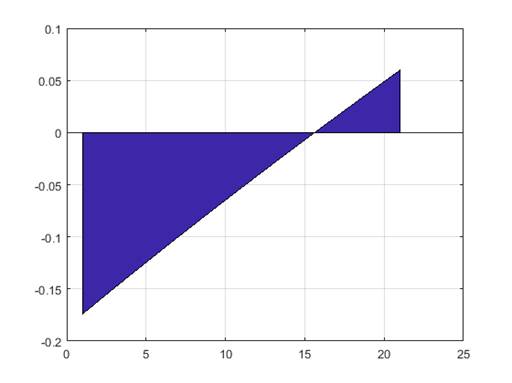
получим ответ

U1 =

-0.0109

Далее вычислим методом Симпсона:

u=@(x) sqrt(x)-cos(sqrt(x));

integral(u,0.4,0.6, 'AbsTol', 15e-4)

ans =

-0.0109

3) Вычисление двойного интеграла 3-D функции :

x=-5:0.1:5;

y=-7:0.1:7;

[X,Y]=meshgrid(x,y); %задаем сетку

F=X.^2-Y.^2;

meshz(X,Y,F) %строим график функции

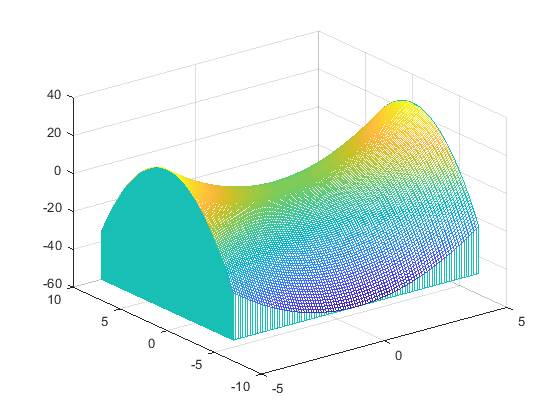
Вычислим двойной интеграл:

Q=trapz(y,trapz(x,F,2))

Q =

-1120

Ответ:-1120 ед.