Хелпикс

Главная

Контакты

Случайная статья



Самостоятельная работа « Свойство функций» ( для базы)



Самостоятельная работа « Свойство функций» ( для базы)

Построить график функции 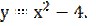Используя график функции исследовать ее по плану, который приведен ниже

План исследования функции по графику:

1. Область определения ( множество значений, которые может принимать х)

2. Область значений( множество значений, которые может принимать у)

3. Нули функции ( найти значения х, при которых у=0)

4. Четность ( по графику функции выяснить четная она или нет: если график симметричен относительно оси Оу, то функция четная, если график симметричен относительно начала координат, то функция нечетная)

5. Промежутки знакопостоянства ( надо выяснить при каких х у больше нуля)

6. Непрерывность ( если график функции можно начертить не отрывая руку от листа бумаги. То это непрерывная функция)

7. Монотонность ( надо выяснить при каких х функция возрастает, при каких убывает)

8. Наибольшее и наименьшее значения ( по графику функции определить наибольшее ( 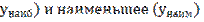значение функции)

9. Ограниченность ( если все значения функции больше некоторого числа, то говорят, что функция ограничена снизу, если все значения функции меньше некоторого числа, то говорят, что функция ограничена сверху. Если функция ограничена и сверху и снизу, то говорят, что функция ограничена)

10.Экстремумы (по графику функции найти точку максимума 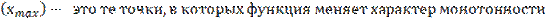 с возрастания на убывание и точки минимума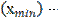

 

Выполняя это задание, ориентируйтесь на образец исследования функции, который был вам прислан ранее :

 

 

Исследовать функцию по графику:

 

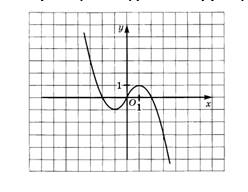
1.D(f): R

2. E(f): R

3. Нули функции: у=0, если х=-2; х=0;х=2

4. Четность: f(х) нечетная, т.к. график функции симметричен относительно начала координат.

5. Промежутки знакопостоянства: а)у>0,если х∈(-∞;−2)∪(0;2)

б) у<0, если х∈-2;0) ∪(2;+ ∞)

6. функция непрерывна

7. Монотонность: а) функция убывает при х∈(-∞;-1); (1;+ ∞)

б) функция возрастает при х∈(-1;-1)

8. Наибольшее,раименьшее значение: унаиб,унаим−нет

9. Ограниченность: функция не ограничена

10. Экстремумы: х𝑚𝑖𝑛=−1,у𝑚𝑖𝑛=−1

х𝑚𝑎𝑥=1,у𝑚𝑎𝑥=1

11.Функция выпукла вниз при х∈(-∞;0), функция выпукла вверх при х∈(0;+∞),

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.