Билет №. Системы счисления.. Теория вероятностей.. Энтропия. Количество информации.

Билет №

1. Системы счисления.

Сложить два числа в пятеричной системе счисления (1234+234=2023). Сложение осуществлять в пятеричной системе счисления.

+

2. Теория вероятностей.

Из слова НАУГАД выбирается наугад одна буква. Какова вероятность того, что это буква А? Какова вероятность того, что это гласная?

P=m/n; p=2/6=1/3; p=3/6=1/2

3. Энтропия. Количество информации.

В ящике имеются 2 белых шара и 4 черных. Из ящика извлекают последовательно два шара без возврата. Найти энтропию, связанную с первым и вторым извлечениями, а также энтропию обоих извлечений.

H =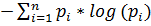

1) =2/6=1/3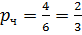

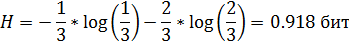
2) Б: p(б/б)=1/5; p(ч/б)=4/5

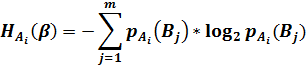
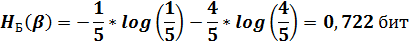
Ч: p(б/ч)=2/5; p(ч/ч)=3/5

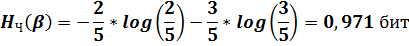
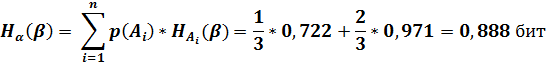
4. Оптимальное кодирование. Построить двоичный префиксный код С с заданной последовательностью L длин кодовых слов: L = (1, 2, 3, 3).

5. Помехоустойчивое кодирование. По каналу связи передавалось кодовое слово, построенное по методу Хэмминга для сообщения a. После передачи по каналу связи, искажающему слово не более чем в одном разряде, было получено слово b. Восстановить исходное сообщение: b = 101010101010001.

n=15

m=11

k=4

s1=1+1+1+1+1+1+0+1=1

s2=0+1+0+1+0+1+0+1=0

s3=0+1+0+1+0+0+0+1=1

s4=0+1+0+1+0+0+0+1=1

s4s3s2s1=1101=13

b = 101010101010101

A=11011010101

С помощью процедуры Хаффмана построить двоичный код с минимальной избыточностью для набора вероятностей Р: Р = (0,5; 0,2; 0,1; 0,09; 0,08; 0,03); Рассчитать среднюю длину и избыточность данного кода.

0.5 0 0.5 0 0.5 0 0.5 0 0.5 0

0.2 11 0.2 11 0.2 11 0.3 10 0.5 1

0.1 1000 0.11 101 0.19 100 0.2 11

0.09 1001 0.1 1000 0.11 101

0.08 1010 0.09 1001

0.03 1011

L = 0.5*1+0.2*2+0.1*4+0.09*4+0,08+4+0,03*4=

Q 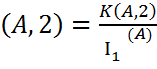– 1=

12 Следующая ⇒