Обработка результатов эксперимента для получения математических моделей

Обработка результатов эксперимента для получения математических моделей

В основе обработки результатов активного и пассивного экспериментов с количественными факторами лежит регрессионный анализ. Он включает метод отыскания параметров математической модели и статистическую обработку данных.

Задачами регрессионного анализа являются:

1. Получение математической модели процесса.

2. Проверка адекватности полученной модели (то насколько полученная мат. модель точно описывает процесс)

3. Оценка влияния каждого фактора на процесс.

Мат.моделью, или регрессионной моделью (одно и то же) называют уравнение, связывающее параметр процесса с факторами или зависимость выходной величины y от варьируемых факторов x₁, x₂, …, x_n.

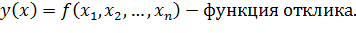
«Построенная регрессионная модель позволяет получить информацию о самом объекте. С помощью мат модели можно легко оценить степень влияния на выходную величину и может послужить для оптимизации процесса.»

Главное требование к модели – способность предсказывать направление дальнейших опытов с требуемой точностью. Если модель соответствует этому – то её называют адекватной.

Модель в виде многочлена первого порядка, или линейная модель выглядит следующим образом:

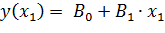– однофакторный;

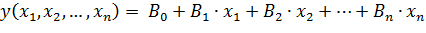– многофакторный;

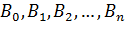– коэффициенты, числовые значения которых определяются по результатам эксперимента.

Линейная модель применяется в следующих случаях:

1. На начальных этапах исследования объекта или в других ситуациях, когда экспериментатора удовлетворяет ограниченная точность линейного приближения

2. При жестком ограничении на количество опытов.

3. Ситуации, когда экспериментатор уверен в достоверности линейной модели.

Модель второго порядка для однофакторного эксперимента:

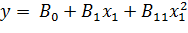– однофакторный.

Модель второго порядка для многофакторного эксперимента:

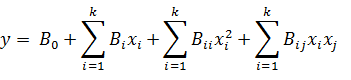
Например, для двухфакторной модели второго порядка модель:

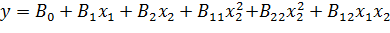
Метод наименьших квадратов для модели с одной переменной:

В данном случае (модель первого порядка с 1 переменной) действие фактора на объект исследования описывается следующей системой нормальных уравнений:

N – число опытов;

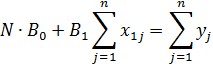
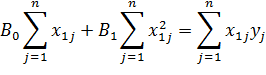
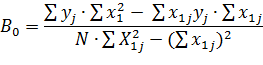
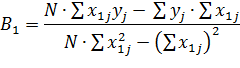
Пример

На специальной установке определялась деформация(y) образца гладким стальным вальцом в зависимости от усилий прижима (x)

№ опыта	Усилие прижима, МПа	№ образца	Полная деформация, мм	~y, мм	Проверка y^, мм
	1,0		0.12 0.07 0.014	0.11
	1.5		0.19 0.17	0.16
			0.225 0.22 0.20	0.215
	2.5		0.31 0.33 0.35	0.33
	3.5		0.39 0.44 0.37	0.4

12 Следующая ⇒