
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример готовой работы. Задание. Необходимый материал. Решение
Пример готовой работы
Задание
Найти производную функции 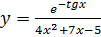
Необходимый материал
Для решения понадобятся правила дифференцирования и таблица производных.
Таблица производных элементарных функций:
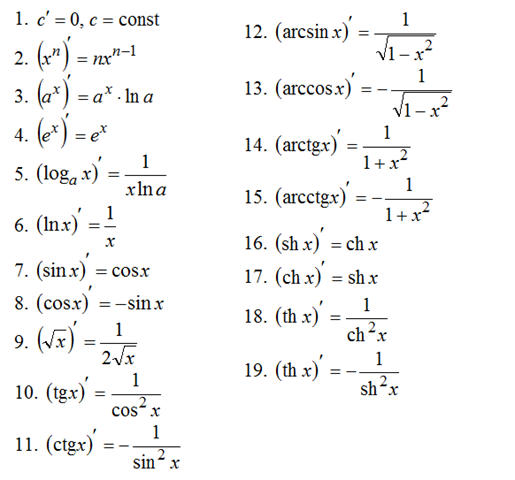
Правила дифференцирования:
1. Постоянный множитель можно вынести за знак производной 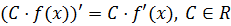
2. Производная суммы (разности) равна сумме (разности) производных:
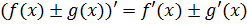
3. Правило дифференцирования произведения двух функций выглядит следующим образом: 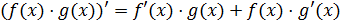
4. Правило дифференцирования частного двух функций выглядит следующим образом:
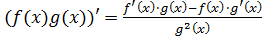
5. Производная сложной функции 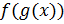 :
:
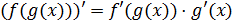
Таблица производных сложных функций:
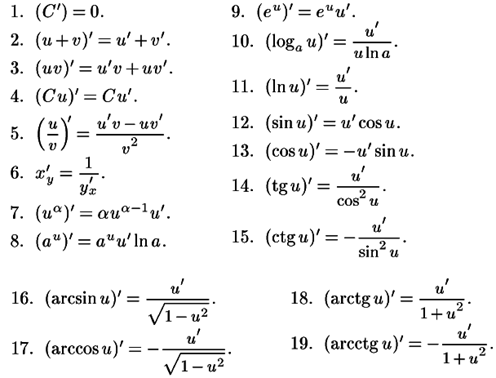
Решение
Функция 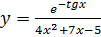 – это частное от двух функций:
– это частное от двух функций: 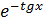 и
и 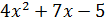 . Применяется формула 4 (производная частного):
. Применяется формула 4 (производная частного):
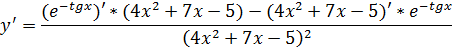
Вычисляем 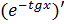 . Это сложная функция, где
. Это сложная функция, где 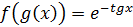 ,
, 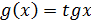 .
.
По формуле 5 правил имеем:
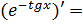 (по таблице сложных функций берем соответствующую формулу №9)
(по таблице сложных функций берем соответствующую формулу №9) 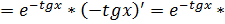 (правило дифференцирования 1, константу -1 выносим за знак производной, производная
(правило дифференцирования 1, константу -1 выносим за знак производной, производная 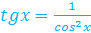 (по таблице элементарных функций))
(по таблице элементарных функций)) 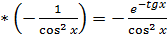
Далее находим 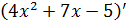 . Применяем формулу производной суммы:
. Применяем формулу производной суммы:
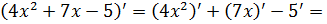 (постоянный множитель выносится за знак производной, применяется формула производной от элементарной функции)
(постоянный множитель выносится за знак производной, применяется формула производной от элементарной функции) 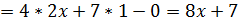 .
.
Итак, получаем:
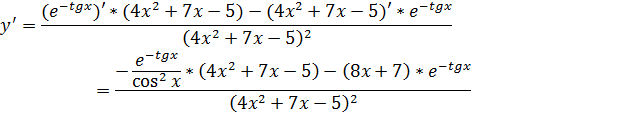
Ответ: 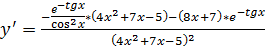 .
.
Дополнительный пример:
Вычислить производную функции 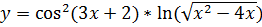
Функция содержит произведение двух сложных функций 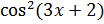 и
и 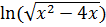 . По формуле производной произведения получаем:
. По формуле производной произведения получаем:
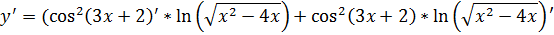
Находим 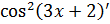 . Сначала вычисляем производную от функции квадрата, затем от косинуса, затем многочлена:
. Сначала вычисляем производную от функции квадрата, затем от косинуса, затем многочлена:
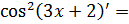 (производная от квадрата, используется 7 формула в таблице производных сложных функций)
(производная от квадрата, используется 7 формула в таблице производных сложных функций) 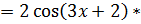 (производная от косинуса – 13 формула в таблице производных сложных функций)
(производная от косинуса – 13 формула в таблице производных сложных функций) 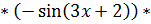 (производная от многочлена, константа 3 выносится за знак производной, производная от х равна 1, производная от константы 2 равна 0)
(производная от многочлена, константа 3 выносится за знак производной, производная от х равна 1, производная от константы 2 равна 0) 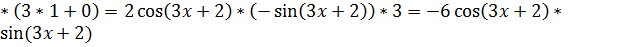 (здесь можно упростить по формуле двойного угла
(здесь можно упростить по формуле двойного угла  )
) 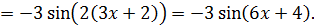
Находим 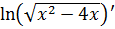 . Вычисляем сначала производную от натурального логарифма, затем от корня, затем от многочлена.
. Вычисляем сначала производную от натурального логарифма, затем от корня, затем от многочлена.
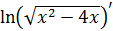 = (производная от натурального логарифма, формула 11 в таблице производных от сложных функций)
= (производная от натурального логарифма, формула 11 в таблице производных от сложных функций) 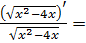 (производная от корня, можно представить корень как степень ½, формула 7 таблицы производных сложных функций)
(производная от корня, можно представить корень как степень ½, формула 7 таблицы производных сложных функций) 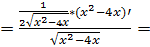 (производная многочлена, разность производных) =
(производная многочлена, разность производных) = 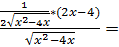 (перенесем знаменатель числителя в знаменатель дроби корень и перемножим)
(перенесем знаменатель числителя в знаменатель дроби корень и перемножим) 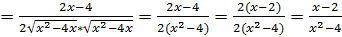
Подставим все в формулу:
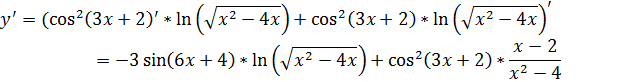
Ответ: 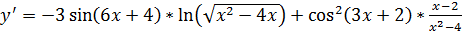 .
.
Задание для самостоятельного решения
Найти производную функции:
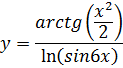
Ответ:
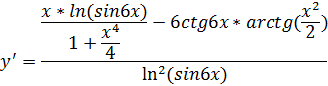
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|