
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
парусные корабли
парусные корабли
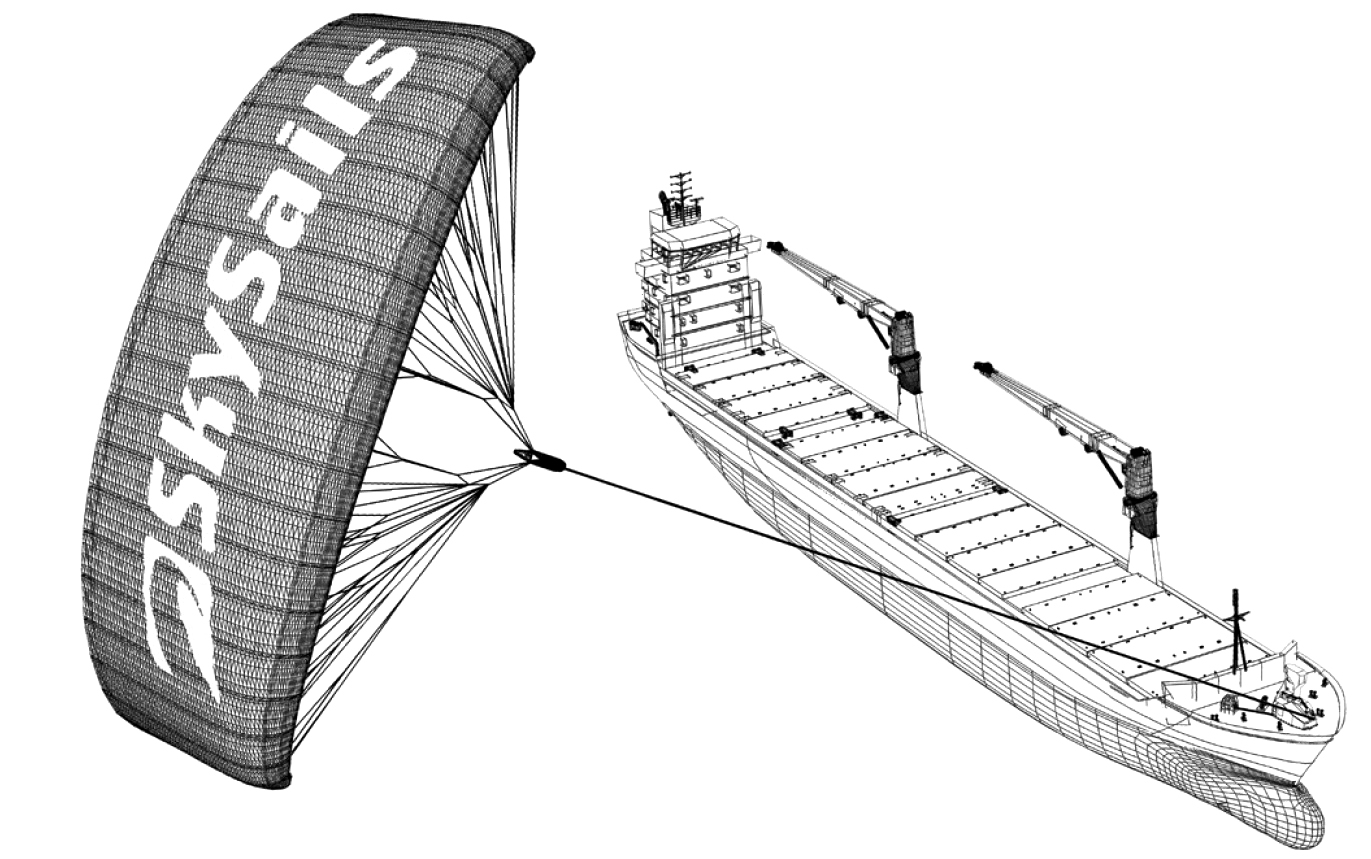
| © by skysails |
Инженеры планируют разработать поддержку кораблей, используя силу ветра. Их предложение заключается в прикреплении к кораблям кайтов (парящих в воздухе парусов) и использовании силы ветра, чтобы уменьшить расход дизельного топлива и его влияние на окружающую среду.
Вопрос 1.
Одно из преимуществ использования кайта заключается в том, что он летает на высоте в 150 м. Там скорость ветра примерно на 25% больше, чем на уровне палубы корабля.
С какой примерно скоростью дует ветер на кайт, когда скорость ветра, измеренная на палубе корабля, равна 24 км/ч?
A 6 км/ч – 16% (ошибка - нашли 25%, вместо 125% от 24 км/ч)
B 18 км/ч – 6% (ошибка - нашли 100%-25%= 75% от 24 км/ч)
C 25 км/ч – 8% (ошибка - не поняли условие задачи)
D 30 км/ч * – 57% (24 1,25 = 30 км/ч ИЛИ 25% от 24= 6, 24+6= 30 км/ч)
E 49 км/ч – 3% (невнимательно прочли условие задачи, сложили 24 км/ч и 25%)
Нет ответа – 3%
Ключевой момент решения – нахождение процентов числа. Задание стандартное, доступно учащимся 5-6 класса. Затруднение вызывает большой текст в описании ситуации, из которого не требуется информация для ответа на данный вопрос. Основные ошибки (ответы А, В, С) заключаются в невнимательном анализе условия задачи, а также в нетвердом знании алгоритмов решения задач на проценты.
Задание отнесено к области «Количество», представленная ситуация «научная», познавательная деятельность «Применять». Результаты невысоки: российские учащиеся – 57%, стран ОЭСР – 60%.
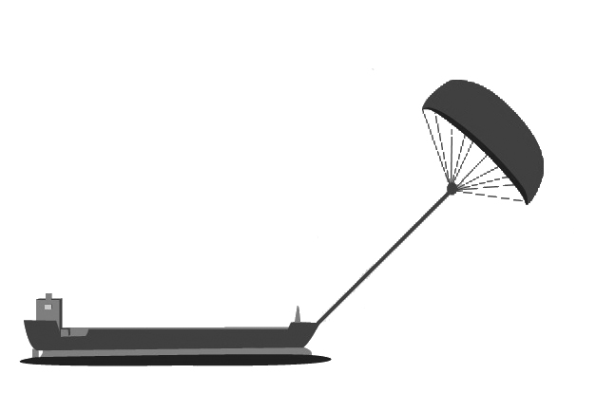 Вопрос 2.
Вопрос 2.
| Примечание: Рисунок сделан не в масштабе. © by skysails |
| 45º |
| 90º |
| 150 м |
| Канаттт |
A 173 м – 15%
B 212 м * – 45%
C 285 м – 18%
D 300 м – 18%
Нет ответа – 4%
Ключевым моментом для решения задачи является применение известной теоремы Пифагора для вычисления длины искомого отрезка, а также знание известного свойства равенства катетов в прямоугольном равнобедренном треугольнике (с углом в 45°). Решение задачи упрощает наличие чертежа, на котором хорошо представлена имеющаяся ситуация и соответствующие данные из условия задачи, а также приведенные варианты ответов. Однако подобных заданий нет в учебниках, форма представления условия задачи совершенно непривычная, поэтому вызвала затруднения у большинства учащихся. Решение: Канат = 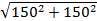 ≈212,13. Сообразуясь с вариантами готовых ответов, следует выбрать ответ В (212).
≈212,13. Сообразуясь с вариантами готовых ответов, следует выбрать ответ В (212).
Задание отнесено к области «Пространство и форма», представленная ситуация «научная», познавательная деятельность «Применять». Результаты невысоки: российские учащиеся – 45%, стран ОЭСР – 50%.
Вопрос 3:
Из-за высокой стоимости дизельного топлива в 0,42 зеда за литр хозяева корабля «Новая волна» думают о том, чтобы снабдить свой корабль кайтом.
Подсчитано, что подобный кайт даёт возможность уменьшить расход дизельного топлива на 20%.
| Название: «Новая волна» |
|
| Тип: фрахтовое судно (сдаётся в наём) | |
| Длина: 117 метров | |
| Ширина: 18 метров | |
| Грузоподъёмность: 12 000 тонн | |
| Максимальная скорость: 19 узлов | |
| Расход дизельного топлива за год без использования кайта: примерно 3 500 000 литров. | |
Стоимость установки на «Новой волне» кайта составляет 2 500 000 зедов.
Через сколько примерно лет экономия на дизельном топливе покроет стоимость установки кайта? Приведите вычисления, подтверждающие ваш ответ.
Количество лет:......................................
Ответ принимается полностью
Код 1: Ответ от 8 до 9 лет сопровождается соответствующими вычислениями.
Возможное решение: Расход топлива за год без паруса: 3,5 миллионов литров, цена литра 0,42, стоимость топлива 3500000 0,42= 1 470 000 зед. 20% экономит парус, тогда экономия 1 470 000  0,2 = 294 000 зед. за год. Стоимость кайта 2 500 000:294 000
0,2 = 294 000 зед. за год. Стоимость кайта 2 500 000:294 000 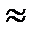 8,5 (лет). Значит, после 8-9 лет покроется стоимость паруса.
8,5 (лет). Значит, после 8-9 лет покроется стоимость паруса.
Это текстовая задача в 3-4 вопроса. В исследовании она отнесена к высшему уровню сложности. Требуется создать модель её решения, применить алгоритм решения задач на проценты и выполнить арифметические действия с многозначными числами. Полученный приближенный ответ (8,5 лет) округлить, учитывая условие задачи. Знания и умения, необходимые для получения ответа формируются в 5-6 классах. В исследовании разрешается использовать калькулятор, что позволяет упростить процесс вычислений и сэкономить время.
Задача отнесена к области «Изменение и зависимости», контекст «научный», познавательная деятельность «Формулировать». Подобных задач нет в российских учебниках. Сложность задачи определяется наличием большого текста, в котором много лишней словесной и количественной информации. Информация представлена в различной форме: в виде текста, количественных данных и рисунков. Данные, нужные для решения, надо извлечь из разных частей текста, в котором имеется количественная информация, ненужная для решения данной задачи. Поэтому не удивительно, что результаты выполнения этого задания невысоки: российские учащиеся – 16%, стран ОЭСР – 15%, максимальный результат у лидирующих стран – 47%.
Задача была бы посильной для российских учащихся 5-6 класса, если бы она была сформулирована в привычной для них редакции, как это делается в российских учебниках: За год двигатель на корабле потребляет 3 500 000 л топлива, 1 литр топлива стоит 0,42 р. Установка паруса на корабле стоит 2 500 000 р. Парус экономит 20% топлива. Через сколько лет экономия топлива покроет стоимость установки паруса?
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
