
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Экономико-математическая модель расстановки флота по схемам движения
Экономико-математическая модель расстановки флота по схемам движения
Сущность задачи состоит в закреплении поименованных типов судов за конкретными схемами движения с позиции избранного критерия оптимальности. В качестве критерия оптимальности принимаем максимум прибыли по сумме всех рейсов. Этот критерий, учитывая особенности различных типов судов, позволяет сопоставить по эффективности варианты их использования на различных схемах. Задачу формируем в терминах линейного программирования. Решение задачи выполняем, используя пакет программ LPX для ПК.
Математическая модель транспортной задачи имеет следующий вид:
Ограничения:
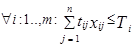
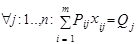
Целевая функция: 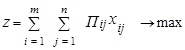
где:
ü i: 1 …, m – индексы, соответствующие типам судов;
ü j: 1 …, n – индексы, соответствующие схемам движения;
ü xij – количество рейсов i-го типа судна по j-й схеме;
ü tij – время рейса i-го типа судна по j-й схеме;
ü Ti – бюджет времени i-го типа судов;
ü Рij – загрузка i-го типа судна по j-й схеме;
ü Qj – количество груза, которое должно быть перевезено по j-й схеме;
ü Пij – прибыль от работы i-го типа судна по j-й схеме.
Для нашего случая целевая функция принимает следующий вид:
z=348,8*x1 + 524,1 *x2 + 45,1*x3 +60,66*x4 + 626,8*x5 +186,8*x6+ 332,2*x7 + -35,2*x8 + 13,31*x9 +418,1*x10 + 72,57*x11 + 275*x12 +-79,45*x13 + -40,57*x14 + 353,6*x15 => max
Ограничения:
45,34*x1 + 58,71*x2 + 13,86*x3 +14,74x4 + 67,3*x5 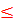 430
430
57,09*x6 + 73,71*x7 +16,3*x8 + 18,21*x9 + 84,28*x10 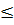 430
430
71,07*x11 + 94,04*x12 + 20,04*x13 + 19,99*x14 + 110,44*x15 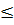 445
445
28 361*x1 + 41 200*x6 +53 973*x11 = 6 936
35 841*x2 + 51 500*x7 + 69 960*x12 = 8 748
7 480*x3 +10 300*x8 + 13 625*x13 = 8 188
6 325*x4 +10 300*x9 + 11 496*x14 = 15 912
43 321*x5 +61 800*x10 + 85 947*x15 = 280 816
Решение:
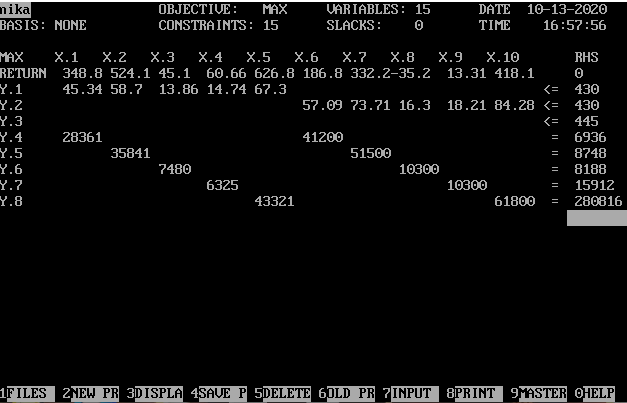
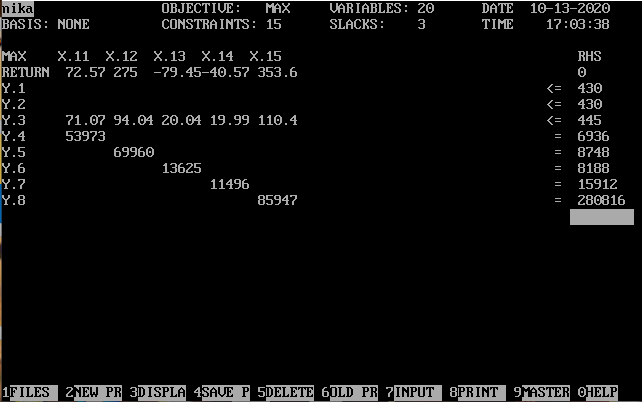
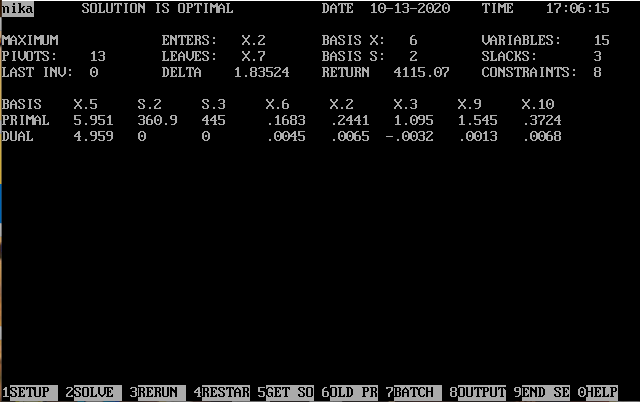
На основании результатов машинного расчета, составляем таблицу.
Поскольку результаты оказались дробными, округляем до целых чисел. При этом учитываем обязательное выполнение ограничений задачи.
|
| Схемы | Неиспользованные ресурсы | |||||
| Тип судна | До округления | После округления | |||||
| ПК |
| 0,2441 | 1,095 |
| 5,951 |
| |
| Варнемюнде | 0,1683 |
|
| 1,545 | 0,3724 | 360,9 |
|
| Астрахань |
|
|
|
|
|
| |
|
|
|
|
|
| |||
| Qплан | 6 936 | 8 748 | 8 188 | 15 912 | 280 816 |
| |
| Qфакт |
|
|
|
|
| ||
Округление результатов машинного решения:
|
| Схемы | Неиспользованные ресурсы | |||||
| Тип судна | До округления | После округления | |||||
| ПК |
| 0,2441 | 1,095 |
| 5,951 | 4,82 | |
| Варнемюнде | 0,1683 |
|
| 1,545 | 0,3724 | 360,9 | 345,72 |
| Астрахань |
|
|
|
|
| ||
|
|
|
|
| ||||
| Qплан | 6 936,00 | 8 748,00 | 8 188,00 | 15 912,00 | 280 816,00 |
| |
| Qфакт | 28 361,92 | 0,00 | 7 480,00 | 12 650,00 | 278 409,60 | ||
Выполнение плана:
| Плановое Q | Возможное Q | % | |
| Алюминий | 50 000,00 | 47 700,00 | 95% |
| Бумага | 60 000,00 | 60 900,00 | 102% |
| Фосфаты | 60 000,00 | 62 660,00 | 104% |
| Трубы | 50 000,00 | 47 700,00 | 95% |
| Удобрения | 50 000,00 | 55 180,00 | 110% |
| Оборудование | 50 000,00 | 52 561,52 | 105% |
Для того, чтоб убрать излишек удобрения, необходимо уменьшить количество груза на 2680 тонн. Тогда выполнение плана составит:
|
| Плановое Q | Возможное Q | % |
| Алюминий | 50 000,00 | 47 700,00 | 95% |
| Бумага | 60 000,00 | 60 900,00 | 102% |
| Фосфаты | 60 000,00 | 62 660,00 | 104% |
| Трубы | 50 000,00 | 47 700,00 | 95% |
| Удобрения | 50 000,00 | 52 500,00 | 105% |
| Оборудование | 50 000,00 | 52 561,52 | 105% |
Прибыль = 4 067 905,8
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|