
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ЛАБОРАТОРНАЯ РАБОТА № 2. Решение задачи оптимального управления на основе принципа максимума Понтрягина». Решение задачи
ЛАБОРАТОРНАЯ РАБОТА № 2
«Решение задачи оптимального управления на основе принципа максимума Понтрягина»
2.1. Цель работы:решить задачу синтеза оптимального управления на основе принципа максимума Понтрягина в задаче быстродействия.
2.2. Исходные данные:
Математическая модель объекта управления: 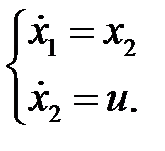
Критерий качества (задача быстродействия): 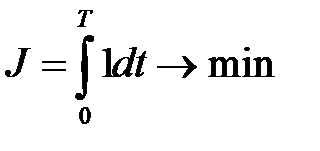 .
.
Ограничение на управляющее воздействие: 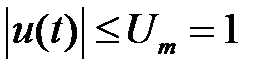 .
.
Граничные условия: 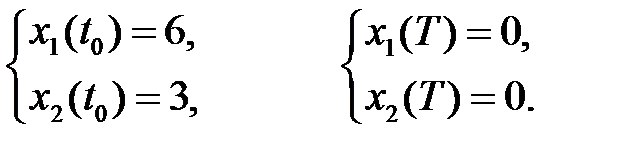
2.3. Решение задачи
Корни характеристического полинома объекта управления:
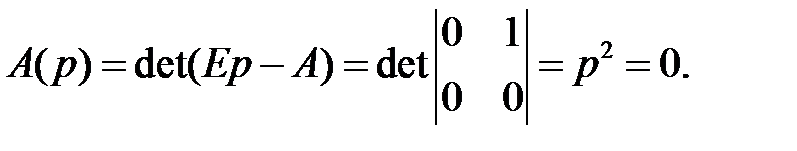
Корни 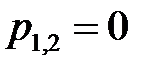 , следовательно, объект является неосциллирующим, и число смен знака управляющего воздействия равно 1.
, следовательно, объект является неосциллирующим, и число смен знака управляющего воздействия равно 1.
Функция Гамильтона: 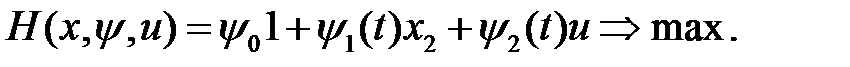
Решение сопряженной системы с учетом функции Гамильтона:
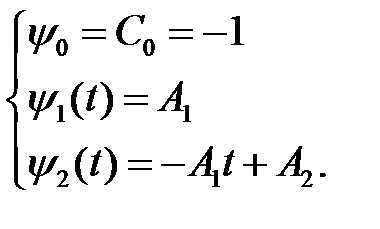
Вид оптимальной программы управления: 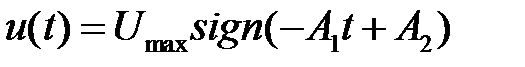 .
.
1) Рассмотрим начальный момент времени 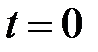 функционирования объекта под действием управляющего воздействия
функционирования объекта под действием управляющего воздействия 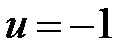 :
:
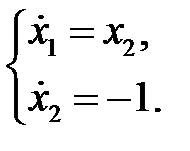
Для определения траектории движения объекта необходимо проинтегрировать его уравнения совместно с граничными условиями на левом конце траектории 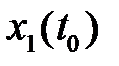 и
и 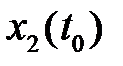 . Для этого можно, например, воспользоваться любым пакетом символьных вычислений. В частности, в пакете MatLab с установленным пакетом расширения Symbolic Math Toolbox данное решение можно найти при помощи приведенных ниже команд, результат будет получен в командном окне
. Для этого можно, например, воспользоваться любым пакетом символьных вычислений. В частности, в пакете MatLab с установленным пакетом расширения Symbolic Math Toolbox данное решение можно найти при помощи приведенных ниже команд, результат будет получен в командном окне
syms t x1(t) x2(t)
u=-1;
x1_0=6;
x2_0=3;
S = dsolve(diff(x1)==x2, diff(x2)==u, x1(0)==x1_0, x2(0)==x2_0)
x1_1(t)=S.x1
x2_1(t)=S.x2
Имеем
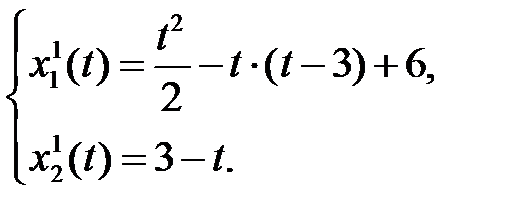
Первое уравнение можно упростить, сгруппировав слагаемые относительно степеней  , тогда имеем окончательный вариант траектории движения системы на интервале времени
, тогда имеем окончательный вариант траектории движения системы на интервале времени 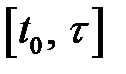 , где
, где 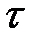 – момент времени переключения знака управляющего воздействия
– момент времени переключения знака управляющего воздействия
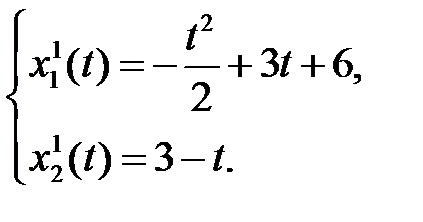
2) Рассмотрим конечный момент времени 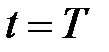 функционирования объекта под действием управляющего воздействия
функционирования объекта под действием управляющего воздействия 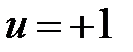 :
:
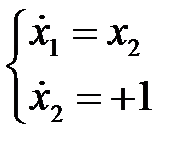
Для определения траектории движения объекта необходимо проинтегрировать его уравнения совместно с граничными условиями на правом конце траектории 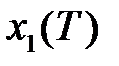 и
и 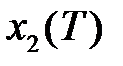 .
.
syms t x1(t) x2(t) T
u=+1;
x1_T=0;
x2_T=0;
S = dsolve(diff(x1)==x2, diff(x2)==u, x1(T)==x1_T, x2(T)==x2_T)
x1_2(t)=S.x1
x2_2(t)=S.x2
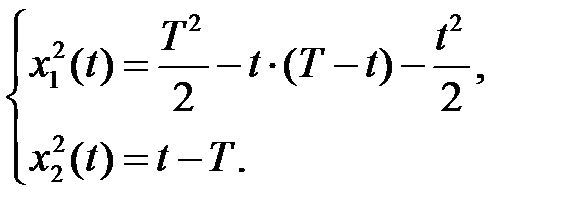
Упростив уравнение системы, получаем следующую систему
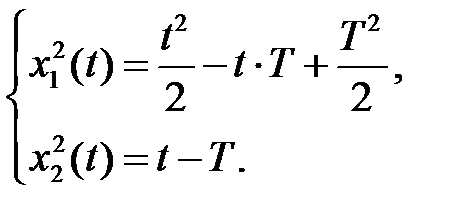
Тогда 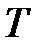 и
и  определим из условия неразрывности решения в момент времени
определим из условия неразрывности решения в момент времени  :
:
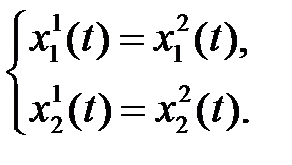
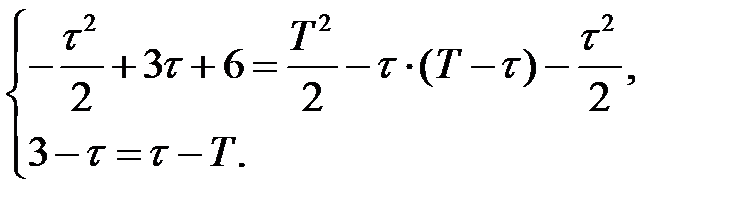
Для этого можно воспользоваться следующим листингом:
syms tau T
Sol=solve(-tau^2/2+3*tau+6==tau^2/2-tau*T+T^2/2,3-tau==tau-T)
Sol.T
Sol.tau
В результате решения квадратного уравнения получены две пары корней:
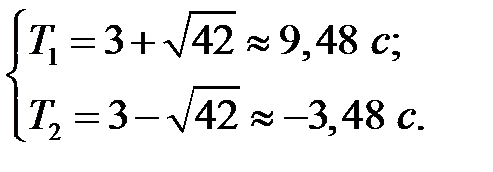
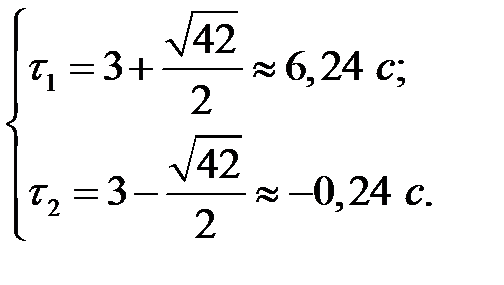
Очевидно, что пара решений 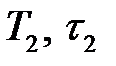 является недопустимой, поскольку время является отрицательным. Тогда имеем
является недопустимой, поскольку время является отрицательным. Тогда имеем
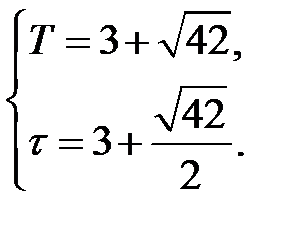
Руководствуясь четвертым условием теоремы Принципа максимума,  , определяются постоянные интегрирования
, определяются постоянные интегрирования  и
и  из уравнений функции Гамильтона в начальный и конечный моменты времени:
из уравнений функции Гамильтона в начальный и конечный моменты времени:
1) 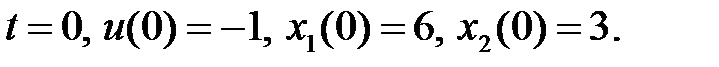
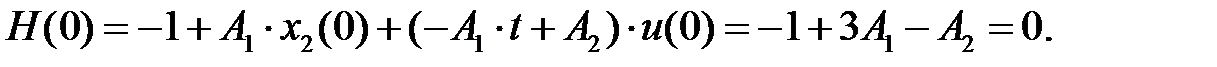
2) 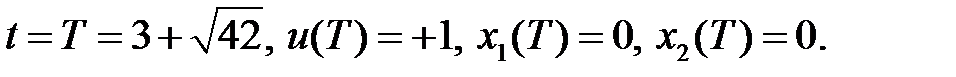
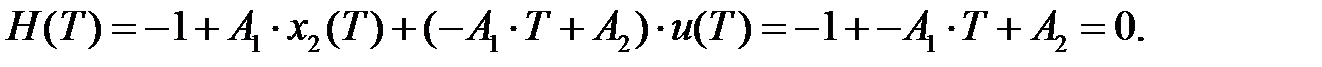
Решая совместно данные два уравнения гамильтониана, необходимо определить значения 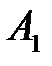 и
и  .
.
syms A1 A2 T
T=3+sqrt(42);
A=solve(-1+3*A1-A2==0,-1-A1*T+A2==0);
A1_opt=eval(A.A1)
A2_opt=eval(A.A2)
В результате получаем:
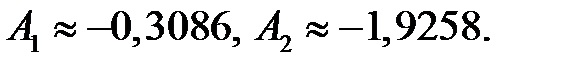
Тогда оптимальная программа управления приобретет вид:
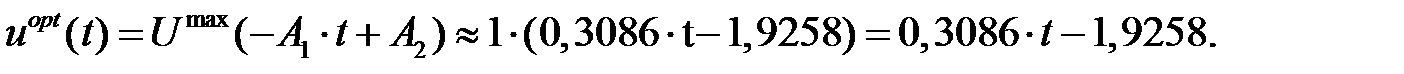
Остается промоделировать оптимальную траекторию движения системы, управление и фазовый портрет движения системы и убедиться в том, что система действительно переходит из начального состояния в конечное с переходом с одной параболы на другую.
2.3. Листинг программы:
clc;
clear all;
close all;
Umax=1;
T=3+sqrt(42);
tau=3+sqrt(42)/2;
A1=-0.3086;
A2=-1.9258;
t=0:0.0001:T;
t1=0:0.0001:tau;
x11=-(t1.^2)/2+3*t1+6;
x21=3-t1;
plot(x11(1),x21(1),'r*','LineWidth',2)
grid on;
hold on;
plot(x11,x21,'-b','LineWidth',2);
xlabel('x_1^{opt}(t)');
ylabel('x_2^{opt}(t)');
title('Фазовый портрет оптимального движения системы');
t2=tau:0.0001:T;
x12=(t2.^2)/2-T*t2+0.5*T^2;
x22=t2-T;
plot(x12(1),x22(1),'ko','LineWidth',2)
plot(x12,x22,'-g','LineWidth',2)
plot(x12(length(x12)),x22(length(x22)),'r*','LineWidth',2)
legend('Краевые условия','I участок','Точка переключения','II участок','Location','NorthWest');
figure(2);
plot(t1,x11,'-b','LineWidth',2);
grid on;
hold on;
xlabel('t');
ylabel('x_1^{opt}(t)');
title('x_1^{opt}(t)');
plot(t1,x21,'-g','LineWidth',2)
plot(t2,x12,'-b','LineWidth',2);
grid on;
hold on;
xlabel('t');
ylabel('x_2^{opt}(t)');
title('x_2^{opt}(t)');
plot(t2,x22,'-g','LineWidth',2);
legend('x_1^{opt}(t)','x_2^{opt}(t)');
plot(tau,0,'ko','LineWidth',2);
plot(T,0,'r*','LineWidth',2);
hT = text(tau+0.2, -0.5, '\tau','FontSize',12);
hT = text(T+0.2, -0.5, 'T','FontSize',12);
plot([tau,tau],[0,x12(1)],'k--');
plot([tau,tau],[0,x22(1)],'k--');
plot([0,T*1.05],[0,0],'k-')
figure(3)
psi2=-A1*t+A2;
plot(t,psi2,'r-','LineWidth',2);
hold on
u_opt=Umax*sign(-A1*t+A2);
plot(t,u_opt,'LineWidth',3);
plot(T,1.1,'w.')
xlabel('t, c');
ylabel('u^{opt}(t), \psi_2(t)');
title('u^{opt}(t), \psi_2(t)');
hold on;
grid on;
legend('\psi_2(t)','u^{opt}(t)','Location','SouthEast');
hT = text(tau+0.2, -0.1, '\tau','FontSize',12);
hT = text(T+0.2, -0.1, 'T','FontSize',12);
plot([T,T],[0,u_opt(length(u_opt))],'k--');
plot([0,T*1.05],[0,0],'k-')
plot([0,tau],[Umax,Umax],'k--')
hT = text(T/40, Umax*1.15, 'U^{max}','FontSize',12);
hT = text(T/40, -Umax*1.15, '-U^{max}','FontSize',12);
На рис. 2.1. показан фазовый портрет оптимальной траектории
Рис. 2.1.Фазовый портрет оптимальной траектории
На рис. 2.2 показана оптимальная траектория движения системы по каждой из переменных состояния.
Рис. 2.2.Оптимальная траектории движения системы
На рис. 2.3 показана сопряженная функция 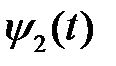 и график оптимального управления
и график оптимального управления 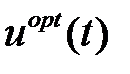 .
.
Рис. 2.3.Сопряженная функция 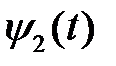 и оптимальное управление
и оптимальное управление
2.4. Контрольные вопросы
1) Что собой представляет гамильтониан?
2) Чем отличается задача оптимального программного управления от задачи синтеза оптимальной стратегии (закона) управления?
3) Что произойдет с оптимальной траекторией движения системы при наличии возмущающих воздействий?
4) Сформулируйте принцип максимума Понтрягина.
5) Как определяется время завершения перевода из заданного начального состояния в начало координат?
6) Что такое неосциллирующая система?
7) Как используется теорема об n-интервалах (Фельдбаума) для получения решения задачи быстродействия на основе принципа максимума Понтрягина?
8) Как сопряженная функция 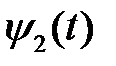 связана с графиком оптимального управления?
связана с графиком оптимального управления?
2.5. Содержание отчета
Отчет о работе должен содержать следующее:
1) Титульный лист.
2) Исходные данные.
3) Гамильтониан.
4) Решение задачи оптимизации.
5) Фазовый портрет оптимального движения системы.
6) Графики оптимальных траекторий движения системы.
7) График оптимального управления и сопряженной функции 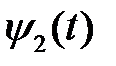 .
.
8) Оптимальное значение критерия эффективности.
9) Выводы по работе.
10) Приложение: листинг для расчета оптимального управления в математическом пакете MatLab.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|