Павлов Денис, БИ-18-1, 1 подгруппа майнора

Павлов Денис, БИ-18-1, 1 подгруппа майнора

Методика.

Для проведения структурного анализа организационной структуры предприятия представим ее в виде графа G = {X, U},

где X - множество вершин (|X | = n), соответствующее множеству структурных элементов;

U – множество ребер (|U| = m), соответствующее множеству связей между структурными элементами предприятия.

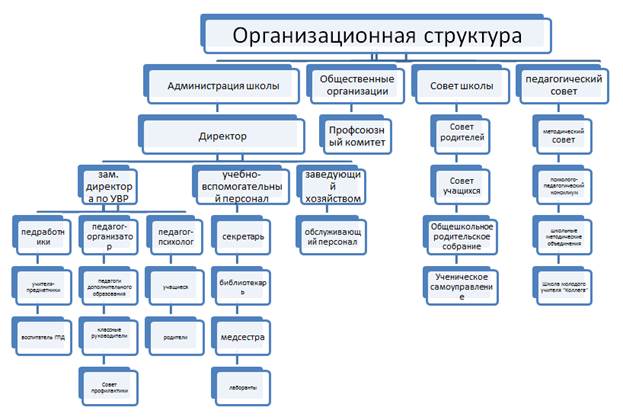
Рисунок 5.9. Организационная структура Школы

Граф G, соответствующий данной школе, показан на рисунке 5.10,

где цифры обозначают: 1 – Организационная структура; 2 – Администрация школы; 3 – Общественные Организации; 4 – Совет Школы; 5 – Педагогический совет; 6 – Зам. директора по УВР; 7 – учебно-вспомогательный персонал; 8 – заведующий хозяйством; 9 – профсоюзный комитет; 10 – совет родителей; 11 –методический совет; 12 –педработники; 13–педорганизатор; 14–педагог-психолог; 15–секретарь; 16–обслуживающий персонал; 17–совет учащихся; 18– педагогический консилиум; 19–учителя-предметники; 20–педагоги дополнительного образования; 21–учащиеся; 22–библиотекарь; 23–общешкольное родительское собрание; 24–школьные методические объединения; 25–воспитатель ГПД; 26–классные руководители; 27–родители; 28–медсестра; 29–ученическое самоуправление; 30–Школа молодого учителя "Коллега"; 31–Совет профилактики; 32–лаборанты;

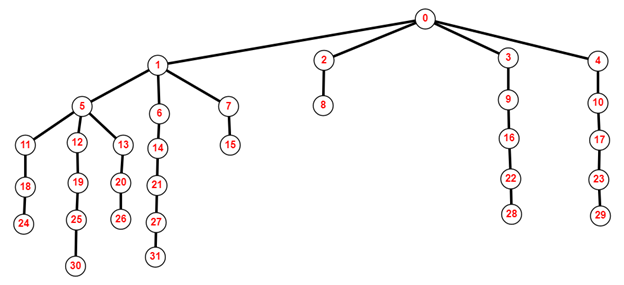
Рисунок 5.10. Структурный граф Школы

Для описания графа G построим матрицу смежности (таблица 5.10), которая для неориентированного графа имеет вид A = || a_ij|| , где a_ij – элементы матрицы смежности, определяемые следующим образом:

1 – при наличии связи между элементами i и j;

a_ij =

0 – при отсутствии связи.

Определим алгоритм проведения структурной диагностики.

1. По матрице смежности определим ранг каждого элемента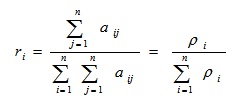

Для нашего случая ∑∑ a_ij = 20. Ранги структурных элементов приведены в последнем столбце таблицы 5.10.

Чем выше ранг элемента, тем более сильно он связан с другими элементами и тем более тяжелыми будут последствия при потере качества его функционирования. В нашем случае наиболее высокий ранг (0,2) имеет первый элемент структуры (директор).

Таблица 5.10. Матрица смежности

p	P^2	r
		0,2
		0,2
		0.1
		0.1
		0.1
		0,2
		0.1
		0.1
		0,05
		0.1
		0.1
		0.1
		0.1
		0.1
		0.1
		0,05
		0.1
		0.1
		0.1
		0.1
		0.1
		0.1
		0.1
		0.1
		0,05
		0.1
		0,05
		0.1
		0,05
		0,05
		0,05
		0,05

2. Проверим связность организационной структуры.

Для связных структур (не имеющих обрывов и висячих элементов) должно выполняться условие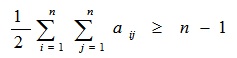

Правая часть неравенства определяет необходимое минимальное число связей в структуре графа, содержащего n вершин.

Для нашего случая n (количество структурных элементов) равно 11 и условие ½ • 62 ≥ 32 – 1, выполняется, то есть структура является связной.

3. Проведем оценку структурной избыточности R, отражающей превышение общего числа связей над минимально необходимым.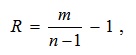

где m – множество ребер графа (1/2 количества связей в матрице смежности);

n – количество вершин (элементов) структуры.

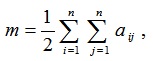
где a_ij– элементы матрицы смежности.

Данная характеристика является косвенной оценкой экономичности и надежности исследуемой структуры и определяет принципиальную возможность функционирования и сохранения связей системы при отказе некоторых ее элементов. Система с большей избыточностью R потенциально более надежна, но менее экономична.

Если R < 0, то система несвязная;

R = 0, система обладает минимальной избыточностью;

R > 0, система имеет избыточность; чем выше R, тем выше избыточность.

Для нашего случая R = ½ • 62 • 1/(32-1) – 1 = 0, то есть структура имеет минимальную избыточность.

4. Определим неравномерность распределения связей – Е. Данный показатель характеризует недоиспользование возможностей данной структуры, имеющей m ребер и n вершин, в достижении максимальной связности.

Величина Е определяется по формул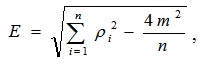е: где 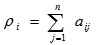- вес i – го элемента, или количество связей i – го элемента со всеми остальными

Для нашего случая E=160-4*(31)^2/32=6,31

Однако, для сравнения различных структур по неравномерности связей, используют относительную величину: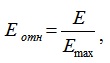

где Е _max– максимальное значение неравномерности связей, которое достигается в системе, с максимально возможным числом вершин, имеющих одну связь.

Величину Е_maxопределяют по формуле: 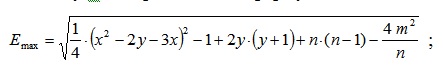где y = m - n; 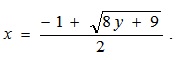Для нашего случая y = 10 – 11 = -1; 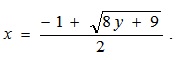= 0 Тогда E= 32*31-4*31^2/32=29,56

Определим величину Е_ОТН для нашего случая. Величина 6,31/29,56=0,21

Е_ОТН для различных типов структур изменяется от 0 (для структур с равномерным распределением связей) до 1. Для оценки неравномерности распределения связей можно воспользоваться следующей шкалой (рис.5.11)

Рисунок 5.11. Шкала для оценивания неравномерности распределения связей

В нашем случае распределение связей в структуре довольно низкое.

5. Определим структурную компактность структуры Q, которая отражает общую структурную близость элементов между собой. Для этого используем формулу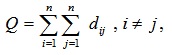

где d_ij – расстояние от элемента i до элемента j, то есть минимальное число связей, соединяющих элементы i и j.

Для определения величины общей структурной компактности построим матрицу расстояний D = || d_ij|| - (табл. 5.11). По таблице определяем – Q = 5066.

Однако для количественной оценки структурной компактности и возможности объективного сравнения различных организационных структур, чаще используют относительный показатель – Q_ОТН, определяемый по формуле: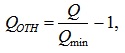

32*31=992

где Q_min = n·(n-1) – минимальное значение компактности для структуры типа “полный граф” (каждый элемент соединен с каждым).

Для нашей структуры Q_min = 32·(32 – 1) = 992. Тогда Q_ОТН= 5066/992 – 1 = 4,1.

Таблица 5.11. Матрица расстояний D

Структурную компактность можно оценить и другой характеристикой – диаметром структуры: d = maxd_ij, равным максимальному значению расстояния d_ij в матрице расстояний. Для нашей структуры d = 32.

С увеличением Q_ОТН и d увеличиваются средние временные задержки при обмене информацией между подразделениями, так как каждый элемент тратит время на обработку информацию и передачу ее дальше, что вызывает снижение оперативности структуры.

Практический опыт и статистические данные показывают: если Q_ОТН = от 0 до 3 – компактность хорошая; Q_ОТН = от 3 до 6 – компактность удовлетворительная; Q_ОТН = больше 6 – компактность неудовлетворительная.

С этой точки зрения структура исследуемого предприятия имеет удовлетворительную оперативность Q_ОТН = 4,1 (максимальную оперативность имеет с полный граф, для которой Q_ОТН =0, а d =1).

6. Для характеристики степени централизации системы используется показатель центральности структурного элемента: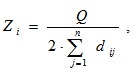

который характеризует степень удаленности i-го элемента от других элементов структуры.

Чем меньше удален i- й элемент от других, тем больше его центральность и тем большее количество связей осуществляется через него. В нашем случае наиболее центральным является первый элемент (директор), для которого ∑ d_ij = 103 = min, то есть он обладает максимальным коэффициентом центральности Z_max= 5066 / (2 · 103) = 24,5.

Сумма первого

Степень центральности в структуре в целом может быть охарактеризована индексом центральности:

Сигма=(n-1)*(2*Zmax-n)/(n-2)*Zmax=(32-1)*(2*24,5-32)/(32-2)*24,5=0,71

Значение степени центральности находится в диапазоне 1 ≥ δ ≥ 0, при этом для структур с равномерным распределением связей δ = 0, для структур, имеющих максимальную степень централизации δ = 1. Для оценки степени центральности можно воспользоваться следующей шкалой (рис.5.12).

Рисунок 5.12. Шкала для оценивания степени центральности

Для нашего случая, высокое значение степени центральности структуры (δ = 0,71) предъявляет высокие требования к пропускной способности центра (элемент 1), через который устанавливается большое число связей, по приему и переработке информации и надежности его функционирования, так как отказ центрального элемента ведет к полному разрушению структуры.

Если в структуре есть центральный элемент, т.е. δ близко к 1, то целесообразно продумать меры по дублированию данного центрального элемента для повышения надежности структуры организации.

Учитывая высокую степень централизации существующей структуры предприятия, рассмотрим и оценим структурные характеристики следующих предлагаемых структур (рис. 5.13).