Решение задач.. А решение прежнее.

№ 6. Решение задач.

Помните ли вы нашу любимую «бубниловку»?

Она звучала так:

«Складываю две дуги, третью цифру вычитаю»

Дуги – это те же самые круги Эйлера, только изображены чуть иначе.

Напоминаю задачи.

Маша пекла пирожки, всего 10 штук. В 6 пирожков она забыла положить начинку, а еще 7 подгорели (учитаны все пирожки). Сколько было подгоревших пирожков без начинки?

Мы делали такую схему. О О О О О О О О О О

Из схемы было видно, что на пересечении находились 3 пирожка.

Что нам было известно?

- Без начинки – 6 (верхняя дуга)

- Горелые – 7 (нижняя дуга)

- Всего – 10.

Требовалось найти пересечение. То есть, A ∩ B

Можно сделать другую схему, с помощью кругов Эйлера.

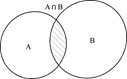
А решение прежнее.

Мы видим, что первый круг накладывается на второй. В этом месте получается двойной слой. Поэтому, если мы просто будем складывать 6+7, то получится гораздо больше, чем 10.

А что такое 10? Это объединение двух множеств: горелых и без начинки.

Если мы возьмем волшебный ластик и начнем стирать верхний слой, то есть все 10 штук, по краям ничего не останется, а в середине окажется нижний слой. Как его найти?

Нужно из суммы 6+7 вычесть 10.

6 + 7 - 10 = 13 – 10 = 3

И обратная задача.

Савва решал примеры. В 10 примерах он накалякал, а еще в 8 забыл написать ответ. Причем в 5 он и накалякал, и ответ забыл написать (учитаны все). Сколько примеров он «решил»?

Когда мы решали с помощью дуг, поступали так: