
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ВВЕДЕНИЕ. Основные определения.
ВВЕДЕНИЕ
Наряду с задачами, в которых необходимо определить максимальные и минимальные значения некоторой функции, в задачах физики нередко возникает необходимость найти максимальные или минимальные значения величинособого рода, называемых функционалами. Функционалами называются переменные величины, значения которых определяются выбором одной или нескольких функций.
Простейший пример функционала - интеграл 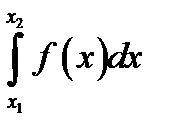 . Каждой функции
. Каждой функции 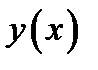 , интегрируемой по Риману на отрезке
, интегрируемой по Риману на отрезке 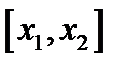 , сопоставляется число – значение интеграла.
, сопоставляется число – значение интеграла.
Вариационное исчисление изучает методы, позволяющие находить максимальные и минимальные значения функционалов. Задачи, в которых требуется исследовать функционал на максимум или минимум, называются вариационными задачам. Многие законы механики и физики сводятся к утверждению, что некоторый функционал в рассматриваемом процессе должен достигать минимума. или максимума. В такой формулировке эти законы носят название вариационных принципов механики или физики.
К числу таких вариационных принципов или простейших следствий из них принадлежат: принцип наименьшего действия, закон сохранения энергии, закон сохранения импульса, закон сохранения количества движения, закон сохранения момента количества движения, различные вариационные принципы классической и релятивистской теории поля, принцип Ферма в оптике, принцип Кастилиано в теории упругости и т. д.
Большое влияние на развитие вариационного исчисления оказали следующие три задачи:
1. Задача о брахистохроне. В 1696 году Иоганн Бернулли опубликовал письмо, в котором предлагал вниманию математиков задачу о линии быстрейшего ската — брахистохроне (βραχιστοζ – кратчайший, χρονοζ - время). Среди всех кривых в вертикальной плоскости 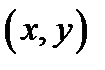 , соединяющих точки
, соединяющих точки 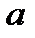 и
и 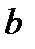 , найти ту, по которой материальная частица скатится в кратчайшее время. Предполагается, что на частицу не действуют никакие силы, кроме силы тяжести.
, найти ту, по которой материальная частица скатится в кратчайшее время. Предполагается, что на частицу не действуют никакие силы, кроме силы тяжести.
Сформулируем задачу в виде уравнения. Начало системы координат 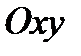 поместим в точку
поместим в точку 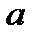 , ось
, ось 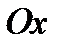 направим по горизонтали, а ось
направим по горизонтали, а ось 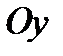 - вниз по вертикали. Пусть точка
- вниз по вертикали. Пусть точка 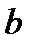 имеет координаты
имеет координаты 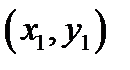 , а уравнение искомой прямой есть
, а уравнение искомой прямой есть 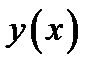 ,
, 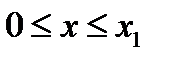 . Частица начинает движение с нулевой скоростью из точки
. Частица начинает движение с нулевой скоростью из точки 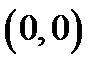 . В соответствии с законом сохранения энергии в точке с координатами
. В соответствии с законом сохранения энергии в точке с координатами 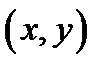 скорость частицы равна
скорость частицы равна
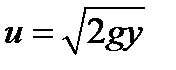 (1)
(1)
где 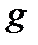 - ускорение свободного падения. С другой стороны
- ускорение свободного падения. С другой стороны
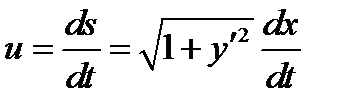 (2)
(2)
Из (1) и (2) следует
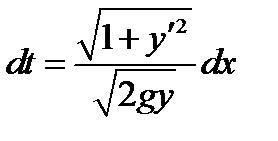
и время прохождения частицы из точки 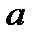 в точку
в точку 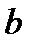 равно
равно
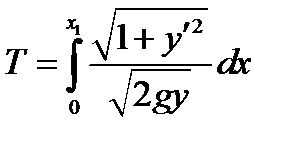 (3)
(3)
Таким образом, задача свелась к нахождению функции 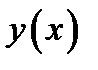 , доставляющей минимум функционалу (3) и удовлетворяющей условиям
, доставляющей минимум функционалу (3) и удовлетворяющей условиям
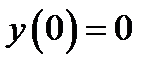 ,
, 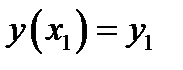
2. Задача о геодезических линиях. Требуется определить линию наименьшей длины, соединяющую две заданные точки на некоторой поверхности 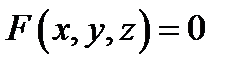 . Такие кратчайшие линии называются геодезическими. Задача сводится к нахождению минимума функционала
. Такие кратчайшие линии называются геодезическими. Задача сводится к нахождению минимума функционала
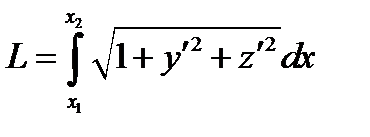
причем функции 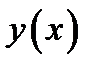 ,
, 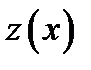 . должны быть подчинены условию
. должны быть подчинены условию 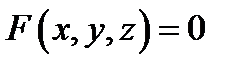 . Эта задача была решена в 1698 году Я. Бернулли, но общий метод решения задач такого типа был дан лишь в работах Л. Эйлера и Ж. Лагранжа.
. Эта задача была решена в 1698 году Я. Бернулли, но общий метод решения задач такого типа был дан лишь в работах Л. Эйлера и Ж. Лагранжа.
1. Основные определения.
Если 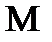 - множество функций и каждой функции
- множество функций и каждой функции 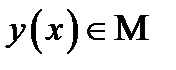 относится определенное число, то говорят, что на множестве
относится определенное число, то говорят, что на множестве 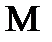 задан функционал. Будем обозначать функционал так
задан функционал. Будем обозначать функционал так 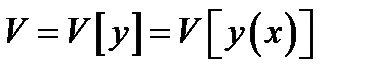 .
.
Если функционал 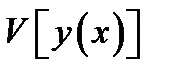 исследуется на экстремум и производится проверка, достигается ли на кривой
исследуется на экстремум и производится проверка, достигается ли на кривой 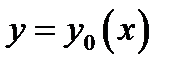 экстремум, то значение
экстремум, то значение 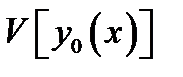 сопоставляется с его значениями на некотором множестве
сопоставляется с его значениями на некотором множестве 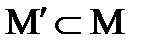 функций
функций 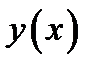 , называемых функциями сравнения, к которому принадлежит и
, называемых функциями сравнения, к которому принадлежит и 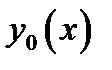 .
.
Множество 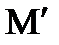 непрерывных функций сравнения
непрерывных функций сравнения 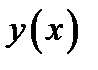 таких, что при некотором значении
таких, что при некотором значении 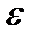 ,
, 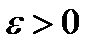
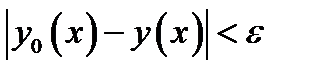 ,
, 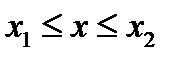
называется окрестностью нулевого порядка, или сильной окрестностью.
Множество 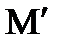 непрерывных функций сравнения
непрерывных функций сравнения 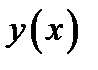 таких, что при некотором значении
таких, что при некотором значении 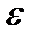 ,
, 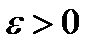
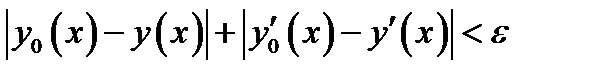 ,
, 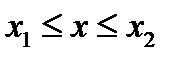
называется окрестностью первого порядка, или слабой окрестностью.
Функционал 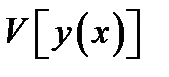 достигает на кривой
достигает на кривой 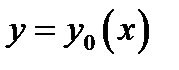 сильного (слабого) максимума, если значения функционала
сильного (слабого) максимума, если значения функционала 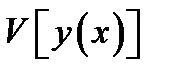 на любой кривой
на любой кривой 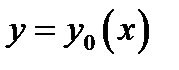 из сильной (слабой) окрестности не больше, чем
из сильной (слабой) окрестности не больше, чем 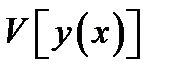 , то есть
, то есть 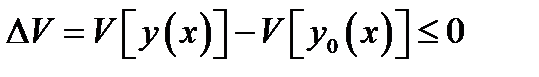 .
.
Если 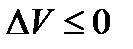 , причем
, причем 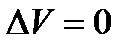 только при
только при 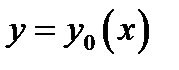 , то говорят, что на кривой
, то говорят, что на кривой 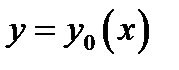 достигается строгий максимум. Аналогично определяется кривая
достигается строгий максимум. Аналогично определяется кривая 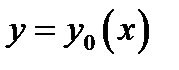 , на которой
, на которой
реализуется минимум. В этом случае 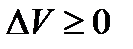 для всех кривых, близких к кривой
для всех кривых, близких к кривой 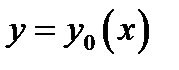 .
.
Всякий сильный экстремум является в то же время и слабым экстремумом. Действительно, если кривая 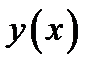 принадлежит слабой окрестности кривой
принадлежит слабой окрестности кривой 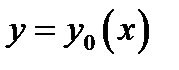 , то она принадлежит и сильной окрестности. Однако возможно, что на кривой
, то она принадлежит и сильной окрестности. Однако возможно, что на кривой 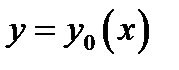 достигается слабый максимум (минимум) но не достигается сильного максимума (минимума).
достигается слабый максимум (минимум) но не достигается сильного максимума (минимума).
При постановке задач вариационного исчисления должно указываться, какого характера экстремум разыскивается и в каком классе функций.
Приращениемили вариацией 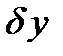 аргумента
аргумента 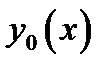 функционала
функционала 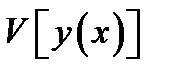 называется разность между двумя функциями
называется разность между двумя функциями 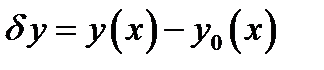 . При этом предполагается, что
. При этом предполагается, что 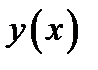 изменяется произвольно в некотором классе функций.
изменяется произвольно в некотором классе функций.
Функционал называетсянепрерывным в сильной (слабой) окрестноститочки (функции) 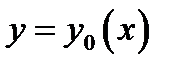 , если для любого положительного
, если для любого положительного 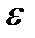 можно подобрать
можно подобрать 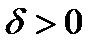 такое, что
такое, что
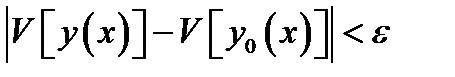
при любой функции 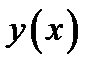 из сильной (слабой) окрестности.
из сильной (слабой) окрестности.
Линейным функционалом называется функционал 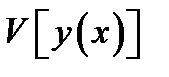 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
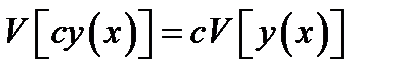
где с — произвольная постоянная и
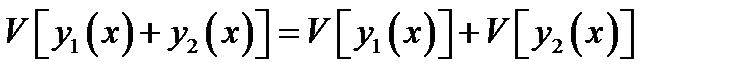
Примером линейного функционала является
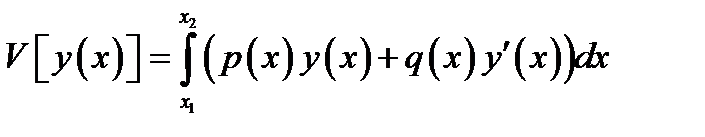
Если приращение функционала
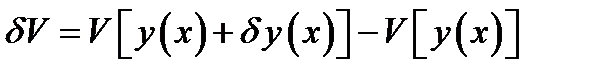
можно представить в виде
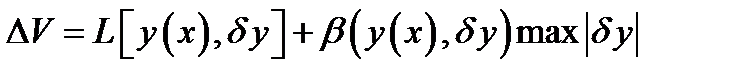
где 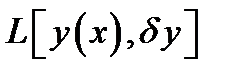 — линейный по отношению к вариации аргумента
— линейный по отношению к вариации аргумента 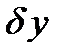 функционал,
функционал, 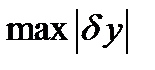 - максимальное значение
- максимальное значение 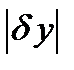 и
и 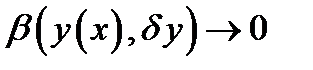 при
при 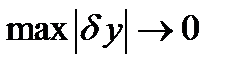 , то линейная по отношению к
, то линейная по отношению к 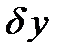 часть приращения функционала, т. е.
часть приращения функционала, т. е. 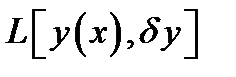 , называется вариацией функционалаи обозначается
, называется вариацией функционалаи обозначается 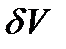 .
.
Вариация функционала — это главная, линейная по отношению к 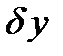 , часть приращения функционала. При исследовании функционалов вариация играет такую же роль, какую играет дифференциал при исследовании функций.
, часть приращения функционала. При исследовании функционалов вариация играет такую же роль, какую играет дифференциал при исследовании функций.
Вариацию функционала можно вычислять следующим образом. Задаем вариацию 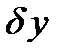 аргумента
аргумента 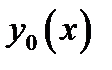 . Определим семейство допустимых функций сравнения
. Определим семейство допустимых функций сравнения 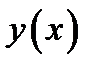 в виде
в виде 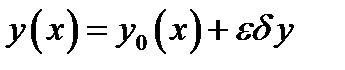 , где
, где 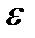 - переменный числовой параметр. Вариация аргумента
- переменный числовой параметр. Вариация аргумента 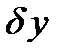 в данном семействе допустимых функций не изменяется. Если функционал имеет вариацию, то его приращение при заданном значении
в данном семействе допустимых функций не изменяется. Если функционал имеет вариацию, то его приращение при заданном значении 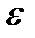 имеет вид
имеет вид
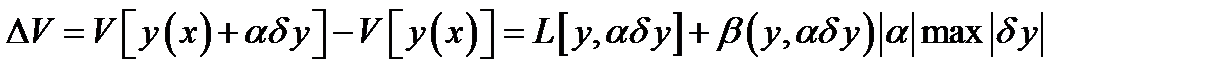 (4)
(4)
где
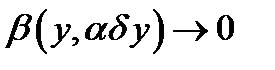 при
при 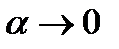 (5)
(5)
а 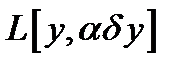 - линейный функционал по отношению к
- линейный функционал по отношению к 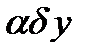 , т.е.
, т.е.
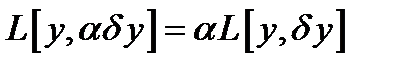 (6)
(6)
Из (4) – (6) следует
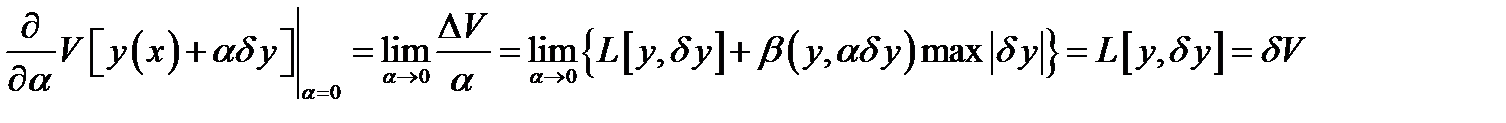
Итак, вариация функционала равна
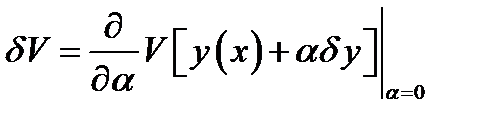
Теорема. Если функционал 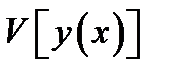 , имеющий вариацию, достигает максимума или минимума при
, имеющий вариацию, достигает максимума или минимума при 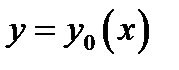 , где
, где 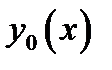 — внутренняя точка области определения функционала, то при
— внутренняя точка области определения функционала, то при 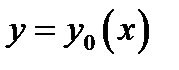
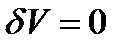 (7)
(7)
Доказательство. При фиксированных 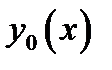 и
и 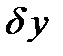 значение
значение 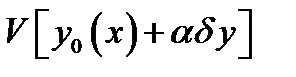 является функцией
является функцией 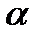 , которая при
, которая при 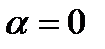 , по предположению, достигает максимума или минимума, следовательно, производная
, по предположению, достигает максимума или минимума, следовательно, производная
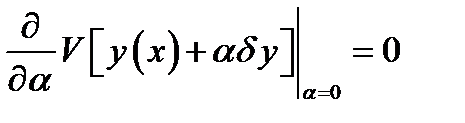 , или
, или 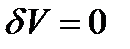
Итак, на кривых, на которых достигается экстремум функционала, его вариация равна нулю.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|