
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ЧИСТАЯ СТРАНИЦА
Сұрақ 1.
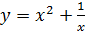 қисықтың теңдеуі берілген. х=2 нүктесіндегі қисықтың теңдеуі берілген. х=2 нүктесіндегі 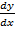 табыңыз.
Жауабы___________________[3] табыңыз.
Жауабы___________________[3]
| Емтихан алушыға |
Сұрақ 2.
модулі бар келесі теңдеуді шешіңіз: 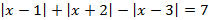 Жауабы___________________[5]
Жауабы___________________[5]
| Емтихан алушыға |
Сұрақ 3.
(a) α және β 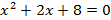 теңдеуінің түбірлері. теңдеуінің түбірлері.
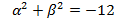 болатынын көрсетіңіз.
[3]
(b) болатынын көрсетіңіз.
[3]
(b) 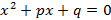 квадраттық теңдеуінің түбірлері квадраттық теңдеуінің түбірлері 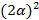 және және 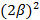 . p мен q -дің мәндерін табыңыз.
Жауабы___________________[2] . p мен q -дің мәндерін табыңыз.
Жауабы___________________[2]
| Емтихан алушыға |
Сұрақ 4.
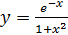 қисықтың теңдеуі берілген. Р нүктесінде қисықтың кризистік нүктесі бар. Р нүктесінің координатасын табыңыз.
Жауабы___________________[5] қисықтың теңдеуі берілген. Р нүктесінде қисықтың кризистік нүктесі бар. Р нүктесінің координатасын табыңыз.
Жауабы___________________[5]
| Емтихан алушыға |
Сұрақ 5.
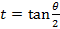 ауыстыруын қолданып, ауыстыруын қолданып, 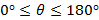 аралығында аралығында 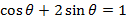 теңдеуді шешіңіз.
Жауабы___________________[5] теңдеуді шешіңіз.
Жауабы___________________[5]
| Емтихан алушыға |
Сұрақ 6.
(a) Р (2; 4; 0) нүктелері арқылы өтетін және 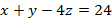 теңдеуімен берілген П жазықтығына перпендикуляр болатын түзудің теңдеуін жазыңыз.
Жауабы___________________[2]
(b) Р нүктесінен П жазықтығына дейінгі қашықтықты табыңыз.
Жауабы___________________[4] теңдеуімен берілген П жазықтығына перпендикуляр болатын түзудің теңдеуін жазыңыз.
Жауабы___________________[2]
(b) Р нүктесінен П жазықтығына дейінгі қашықтықты табыңыз.
Жауабы___________________[4]
| Емтихан алушыға |
Сұрақ 7.
(a) 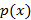 : : 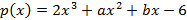 , көпмүшесін табыңыз, мұндағы a және b – тұрақты сандар. , көпмүшесін табыңыз, мұндағы a және b – тұрақты сандар.  екімүшесі көпмүшесінің бөлгіші екендігі белгілі. Ал көпмүшені екімүшесі көпмүшесінің бөлгіші екендігі белгілі. Ал көпмүшені 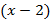 –ге бөлгендегі қалдық 12-ге тең.
Жауабы___________________[4]
(b) Барлық әрекеттерді көрсете отырып және (а) бөліміндегі a мен b –нің мәндерін пайдалана отырып, –ге бөлгендегі қалдық 12-ге тең.
Жауабы___________________[4]
(b) Барлық әрекеттерді көрсете отырып және (а) бөліміндегі a мен b –нің мәндерін пайдалана отырып, 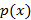 көпмүшесін толығымен көбейткіштерге жіктеңіз.
Жауабы___________________[3] көпмүшесін толығымен көбейткіштерге жіктеңіз.
Жауабы___________________[3]
| Емтихан алушыға |
Сұрақ 8.
(a) 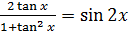 болатынын көрсетіңіз.
Жауабы___________________[3]
(b) Теңдеуді шешіңіз: болатынын көрсетіңіз.
Жауабы___________________[3]
(b) Теңдеуді шешіңіз: 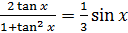 , , 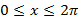 .
Жауабы___________________[4] .
Жауабы___________________[4]
| Емтихан алушыға |
Cұрақ 9.
(a) 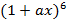 биномдық жіктелуіндегі алғашқы үш мүшесін табыңыз.
Жауабы___________________[2]
(b) a мен b бүтін сандар екені белгілі және биномдық жіктелуіндегі алғашқы үш мүшесін табыңыз.
Жауабы___________________[2]
(b) a мен b бүтін сандар екені белгілі және 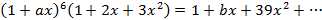 . a мен b мәнін табыңыз.
Жауабы___________________[5] . a мен b мәнін табыңыз.
Жауабы___________________[5]
| Емтихан алушыға |
Сұрақ 10.
(a) Келесі сандардан қанша жеті таңбалы сан құрастыруға болады.
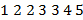 Жауабы___________________[2]
(b) Төмендегі сандардан қанша жұп жеті таңбалы сан құрастыруға болады
Жауабы___________________[2]
(b) Төмендегі сандардан қанша жұп жеті таңбалы сан құрастыруға болады
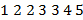 Жауабы___________________[2]
(c) Жоғарыдағы (b) есебіндегі сандардан кері қайтару арқылы кездейсоқ екі сан таңдап алынды. Таңдап алынған екі санның да төртке еселі болу ықтималдығын табыңыз.
Жауабы___________________[4]
Жауабы___________________[2]
(c) Жоғарыдағы (b) есебіндегі сандардан кері қайтару арқылы кездейсоқ екі сан таңдап алынды. Таңдап алынған екі санның да төртке еселі болу ықтималдығын табыңыз.
Жауабы___________________[4]
| Емтихан алушыға |
Сұрақ 11.
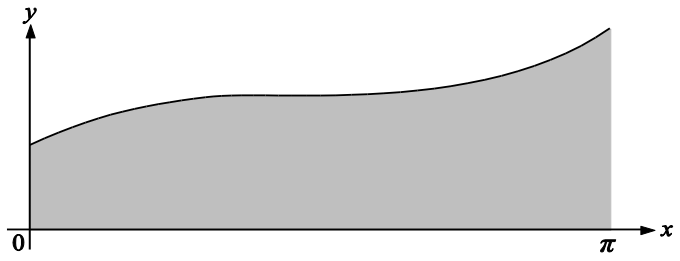 Сызбада
Сызбада 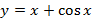 , , 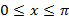 берілген. Боялған бөлігі берілген. Боялған бөлігі 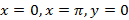 сызықтарымен шектелген. Боялған бөлікті Ox осі бойымен айналдырғанда пайда болған дененің көлемін табыңыз.
Жауабы___________________[10] сызықтарымен шектелген. Боялған бөлікті Ox осі бойымен айналдырғанда пайда болған дененің көлемін табыңыз.
Жауабы___________________[10]
| Емтихан алушыға |
Сұрақ 12.
(a) l түзуінің 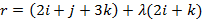 теңдеуімен берілген, ал Р жазықтығының теңдеуі келесідей теңдеуімен берілген, ал Р жазықтығының теңдеуі келесідей 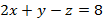 . l мен Р арасындағы бұрышы . l мен Р арасындағы бұрышы 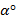 . Жазықтық пен түзудің қиылысу нүктесінің радиус векторын табыңыз.
Жауабы___________________[3] . Жазықтық пен түзудің қиылысу нүктесінің радиус векторын табыңыз.
Жауабы___________________[3]
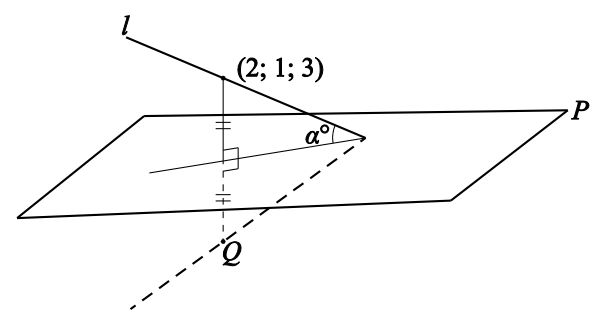 (b) l түзуі P жазықтығына қатысты келесі суреттегідей бейнеленген. (2;1;3) нүктесінің бейнесі болатын Q нүктесінің координатасын табыңыз.
Жауабы___________________[4]
(c) α –ның мәнін табыңыз.
Жауабы___________________[4]
(b) l түзуі P жазықтығына қатысты келесі суреттегідей бейнеленген. (2;1;3) нүктесінің бейнесі болатын Q нүктесінің координатасын табыңыз.
Жауабы___________________[4]
(c) α –ның мәнін табыңыз.
Жауабы___________________[4]
| Емтихан алушыға |
Сұрак 13.
 (a) Суретте
(a) Суретте 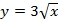 функцияның қисығы бейнеленген. Осы қисыққа жүргізілген (9; 9) нүктесінде жүргізілген жанама Oy осін (0; k) нүктесінде қияды.
Жауабы___________________[5]
(b) Қисық пен жанама және Oy осімен шектелген фигураның айырымын табыңыз.
Жауабы___________________[6] функцияның қисығы бейнеленген. Осы қисыққа жүргізілген (9; 9) нүктесінде жүргізілген жанама Oy осін (0; k) нүктесінде қияды.
Жауабы___________________[5]
(b) Қисық пен жанама және Oy осімен шектелген фигураның айырымын табыңыз.
Жауабы___________________[6]
| Емтихан алушыға |
ЧИСТАЯ СТРАНИЦА
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|