
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Функцияның туындысын табыңыз. . 3 страница
Есепте: 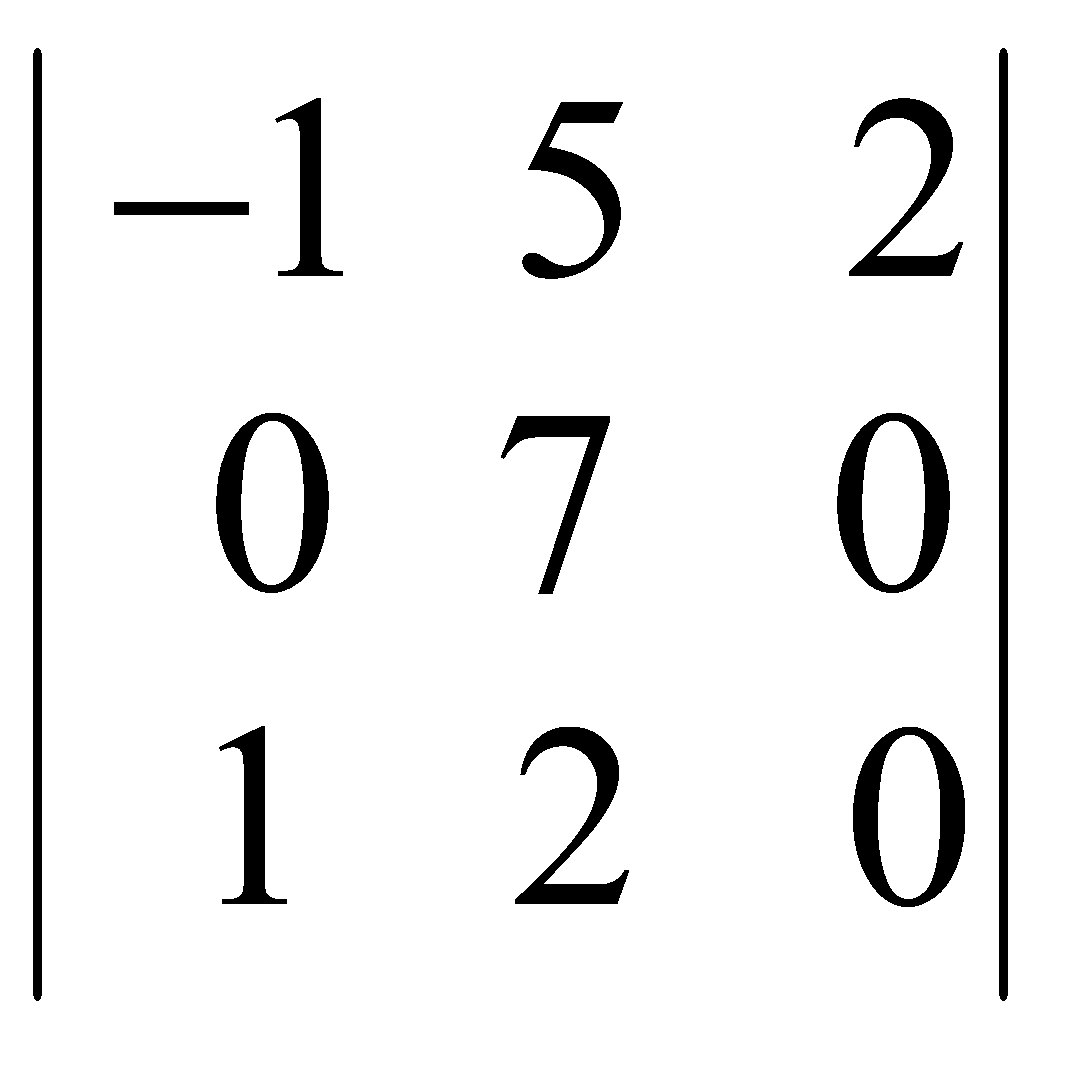 A) –14 D) -28/2 G) -42/3
A) –14 D) -28/2 G) -42/3
Есепте: 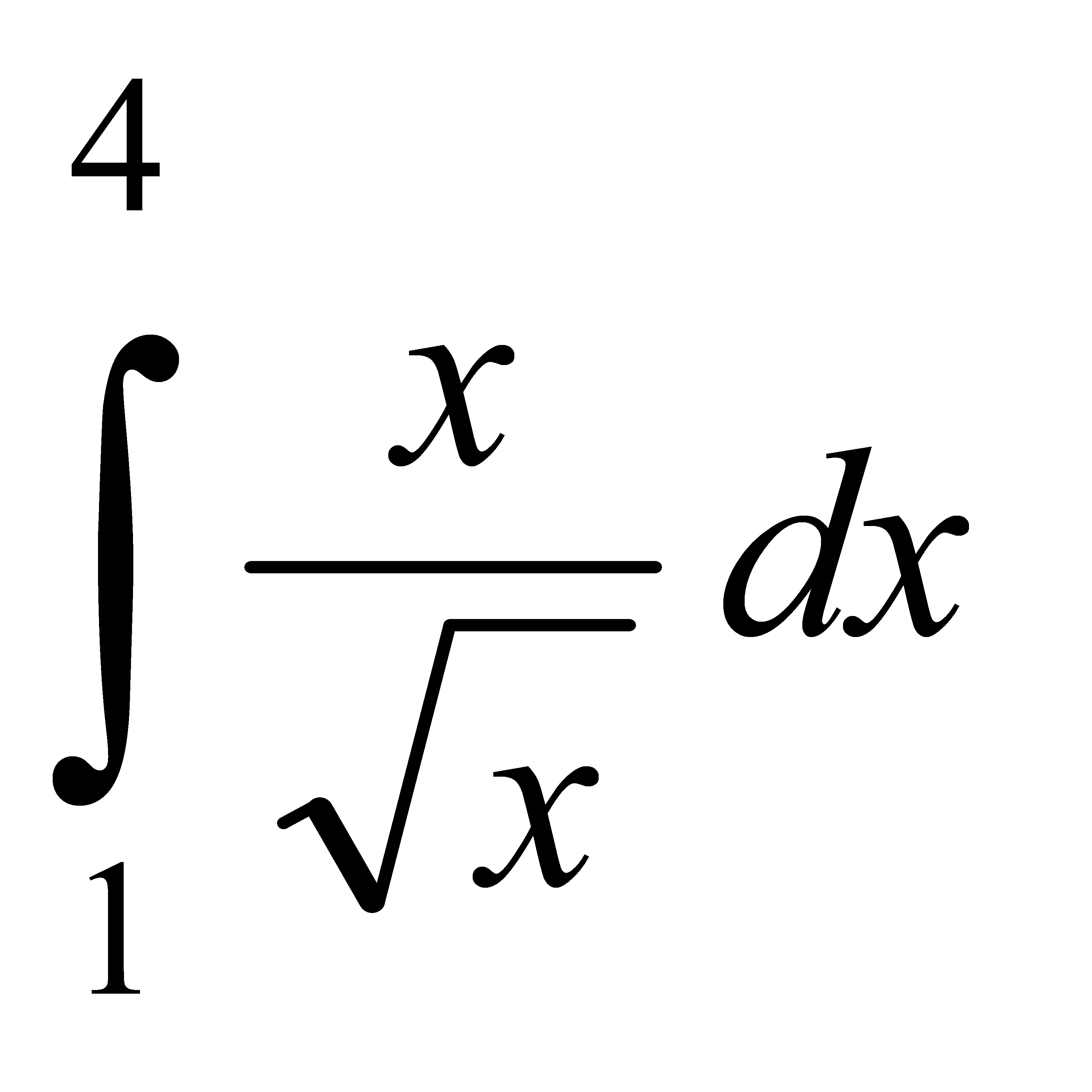 A) 14/3 E) 14 3-1 H) 42/9
A) 14/3 E) 14 3-1 H) 42/9
Есепте: 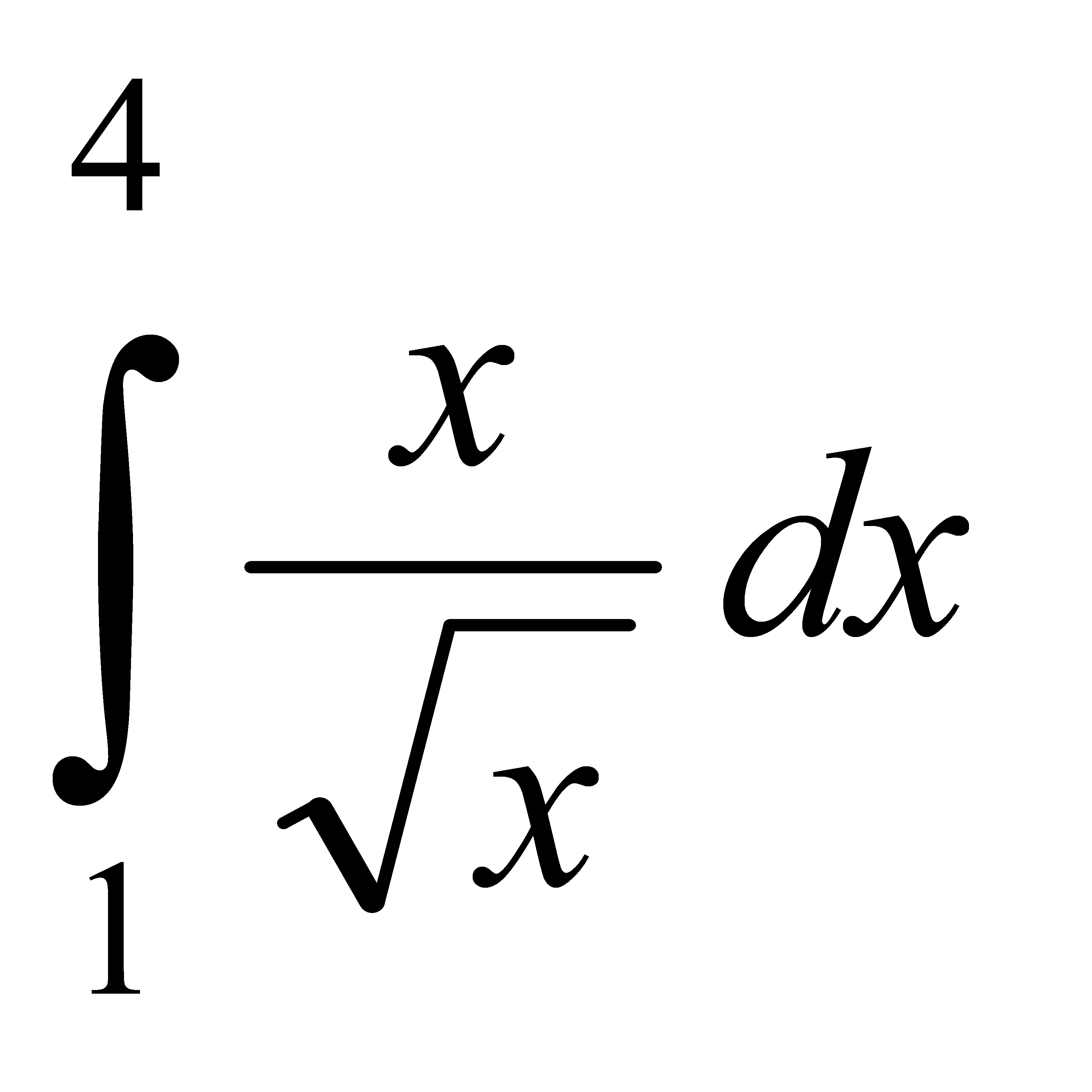 A) 14/3 E) 14 3-1 H) 42/9
A) 14/3 E) 14 3-1 H) 42/9
Есепте: 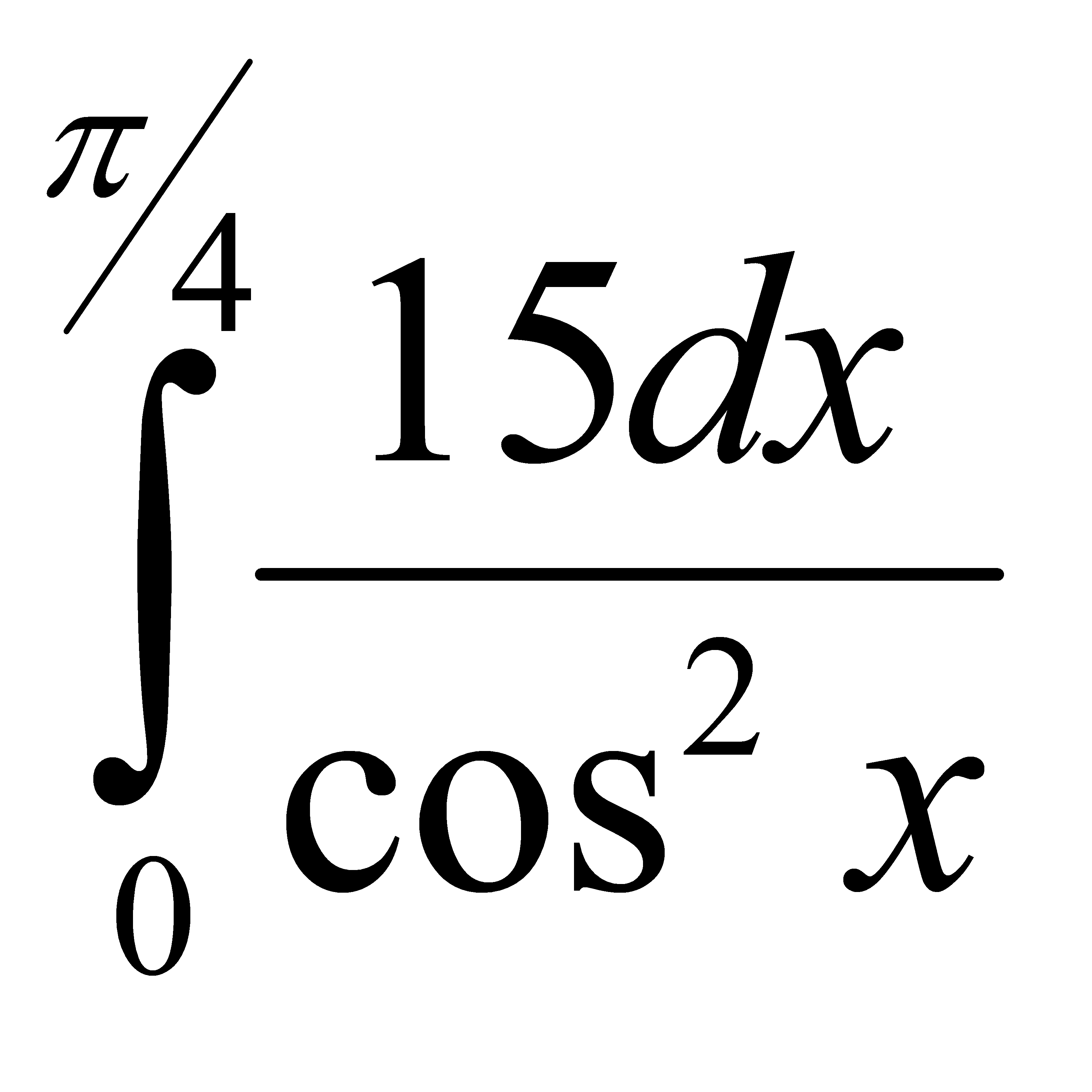 A) 15 C) 30/2 E) 45/3
A) 15 C) 30/2 E) 45/3
Есепте: 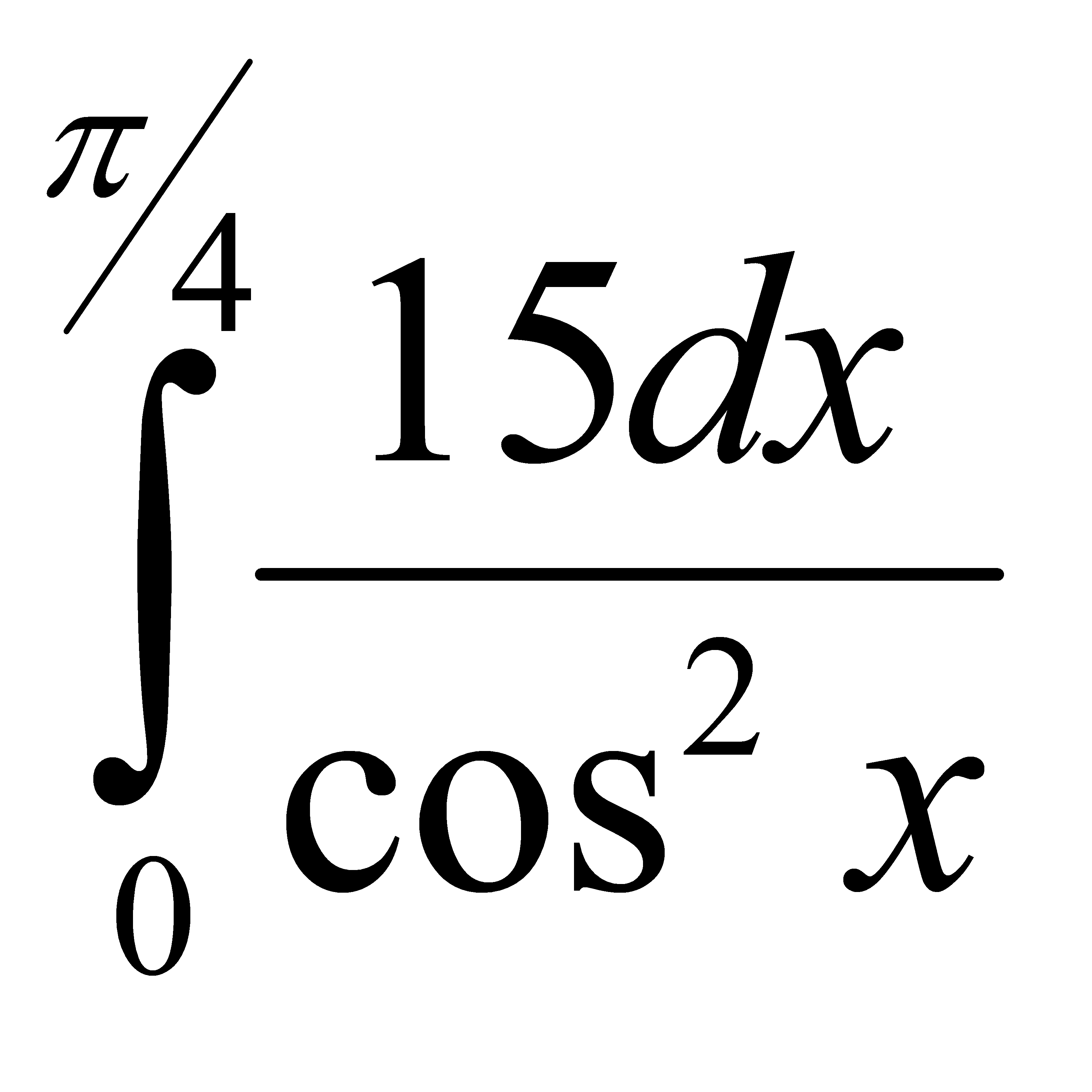 A) 15 C) 30/2 E) 45/3
A) 15 C) 30/2 E) 45/3
Есепте: 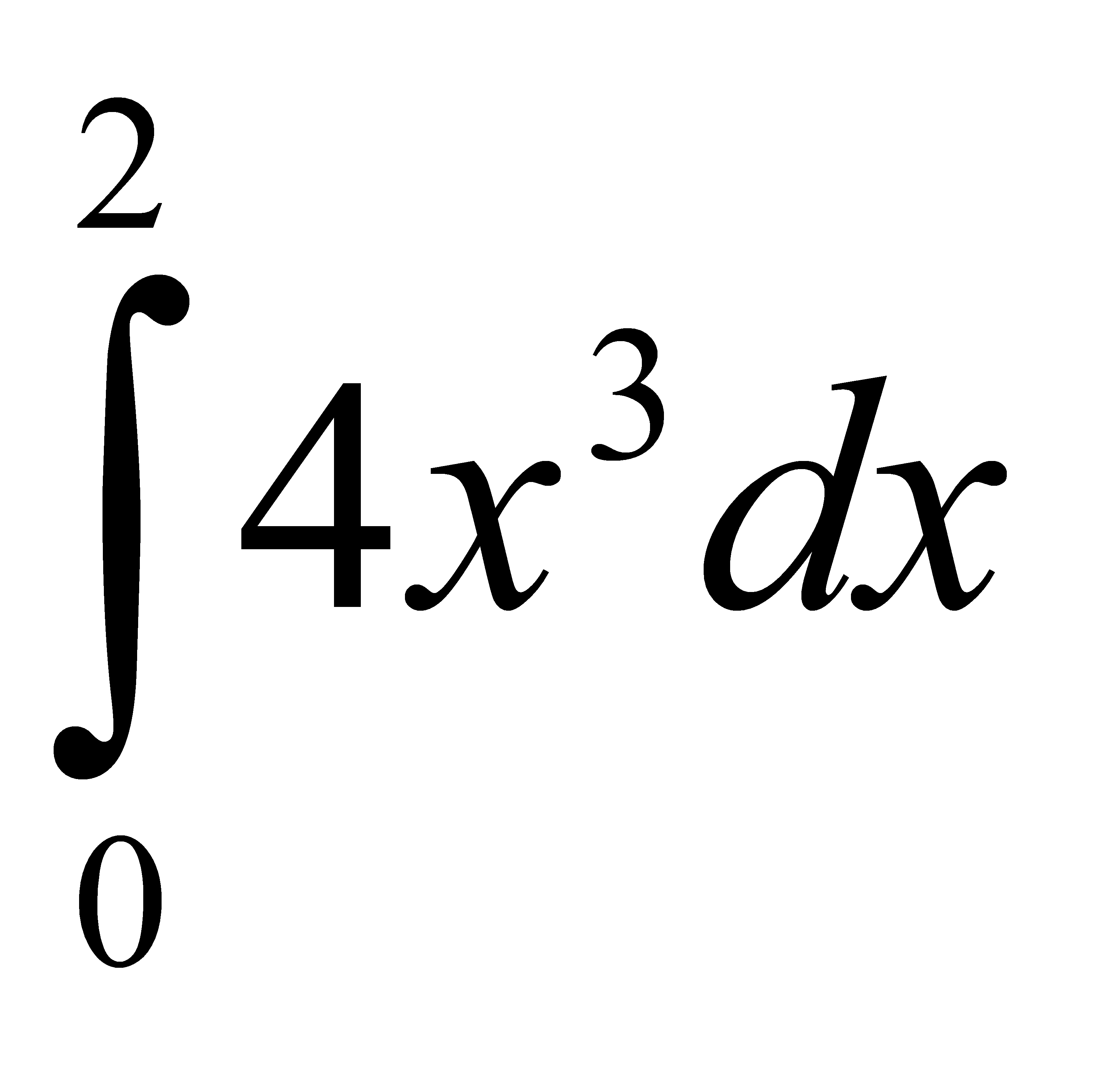 A) 16 D) 32/2 G) 48/3
A) 16 D) 32/2 G) 48/3
Есепте: 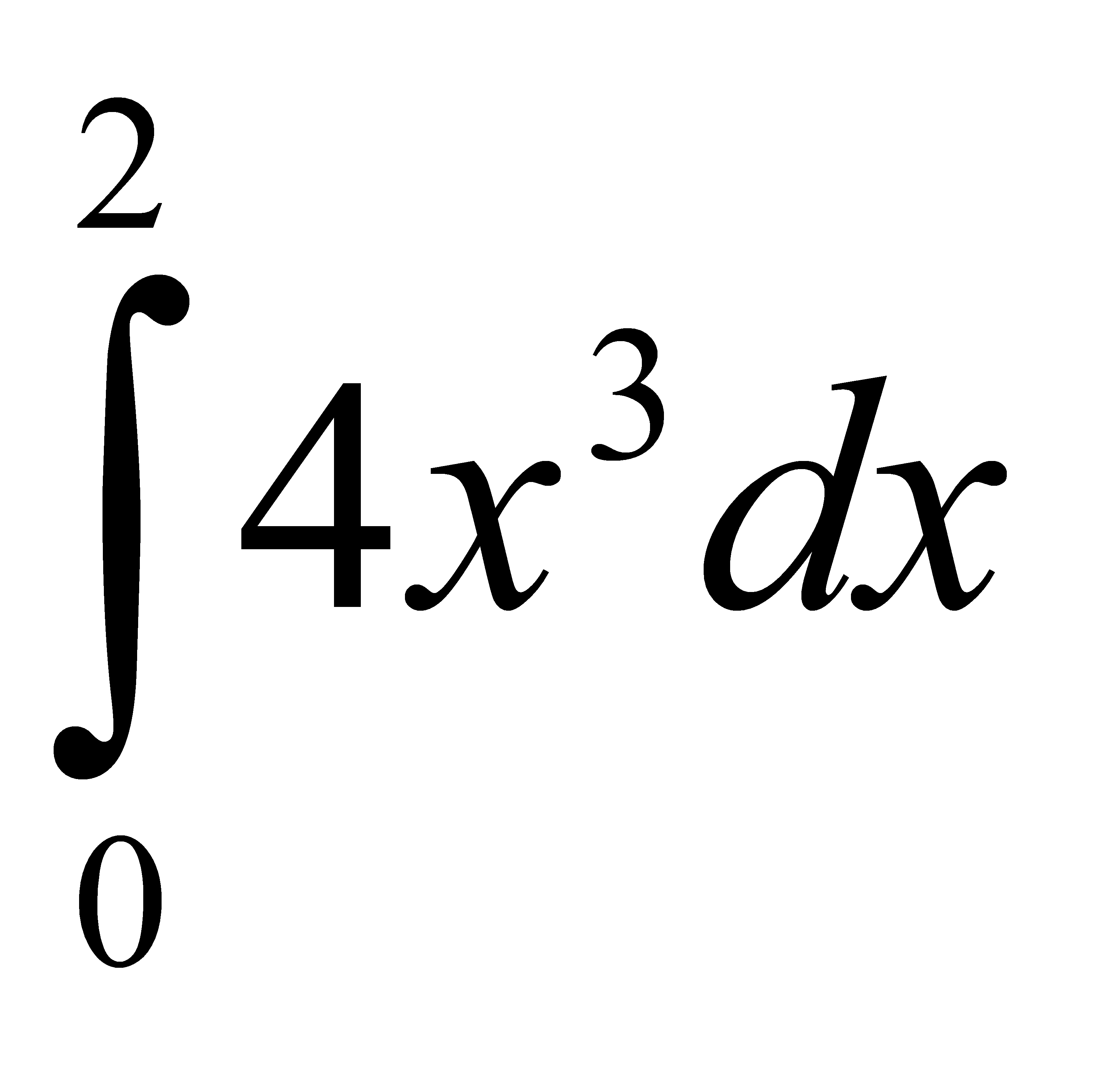 A) 16 D) 32/2 G) 48/3
A) 16 D) 32/2 G) 48/3
Есепте: 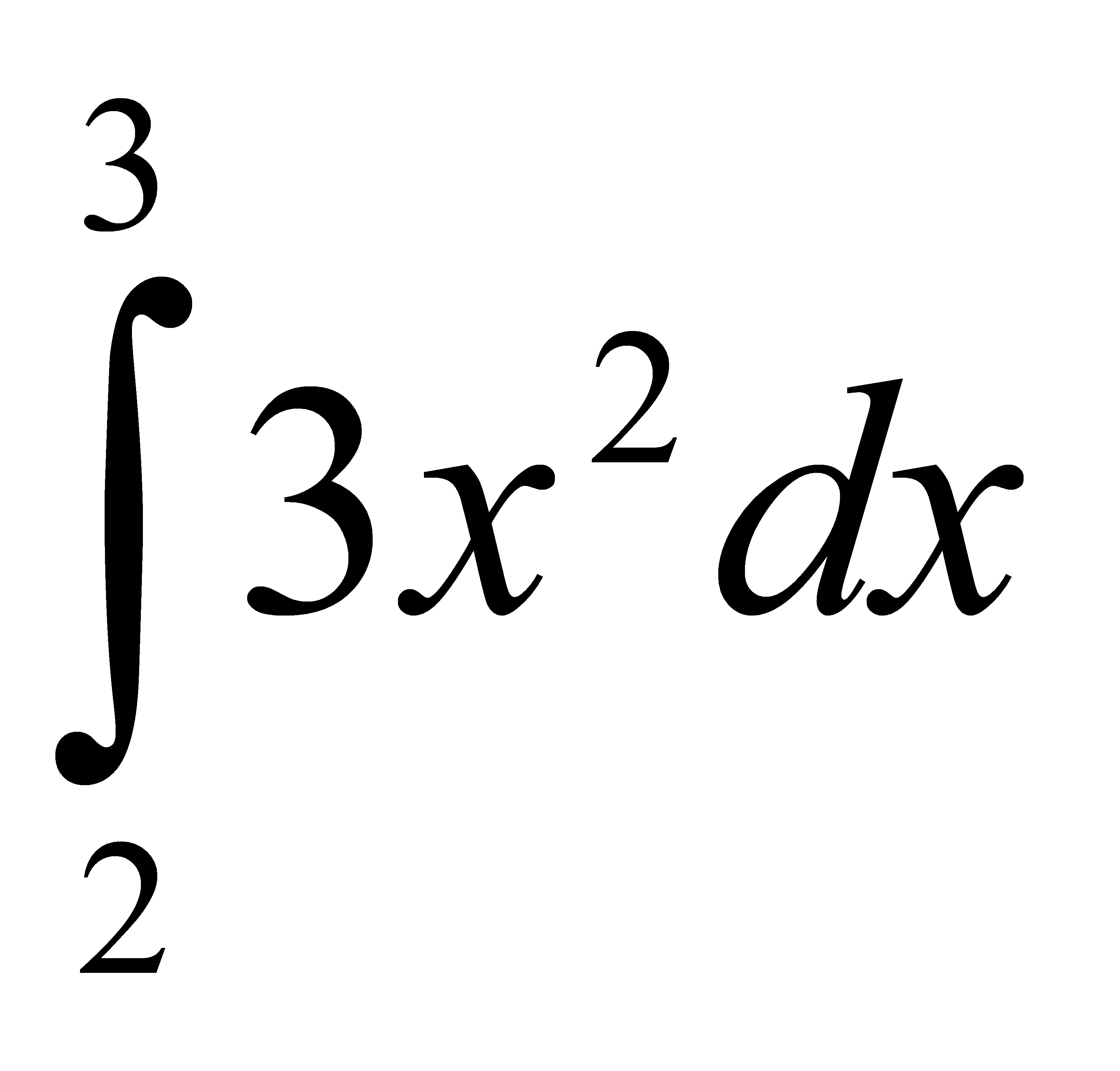 A) 19 G) 38/2 H) 57/3
A) 19 G) 38/2 H) 57/3
Есепте: 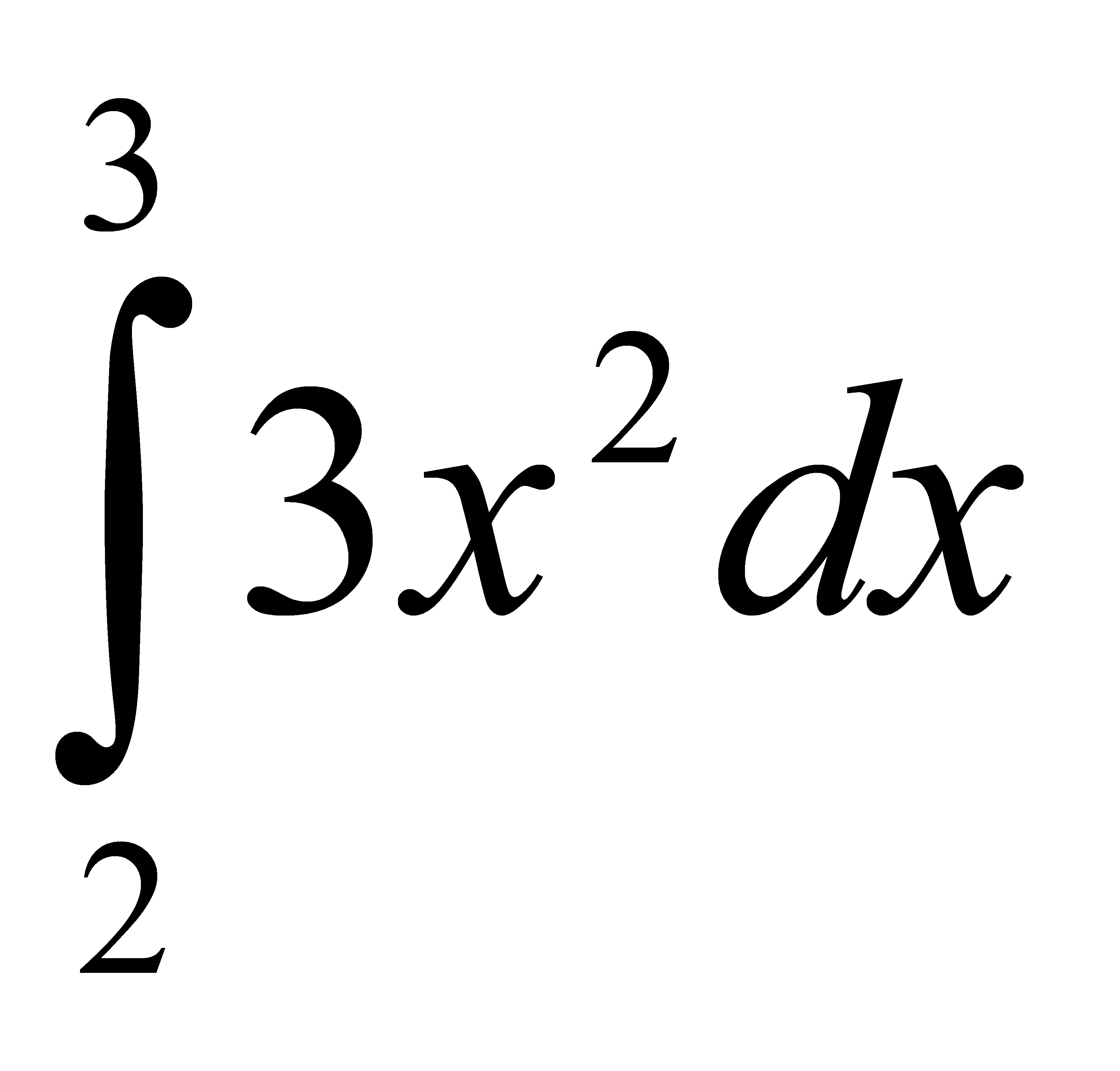 A) 19 G) 38/2 H) 57/3
A) 19 G) 38/2 H) 57/3
Есепте: 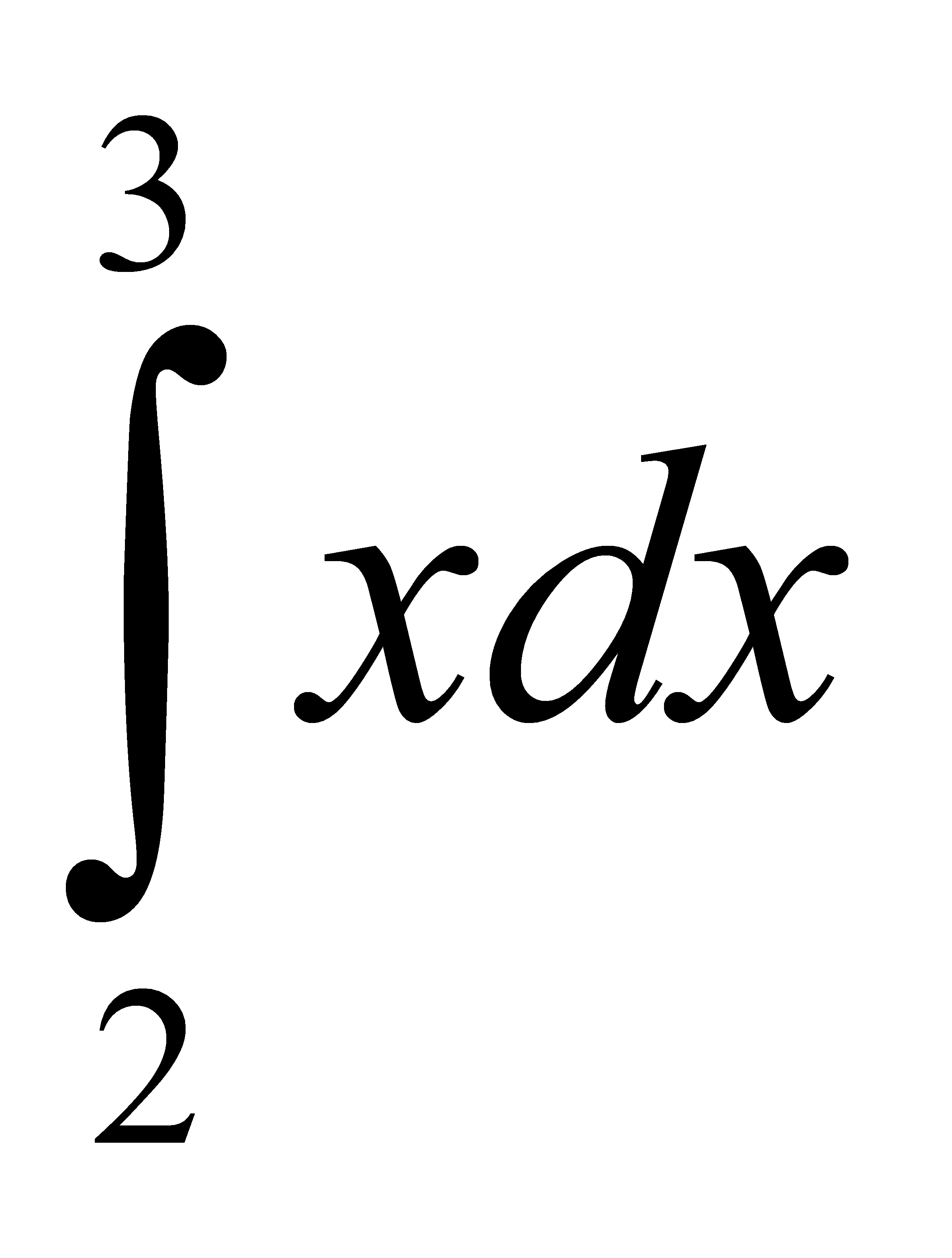 A) 2,5 C) 25/10 H) 5/2
A) 2,5 C) 25/10 H) 5/2
Есепте: 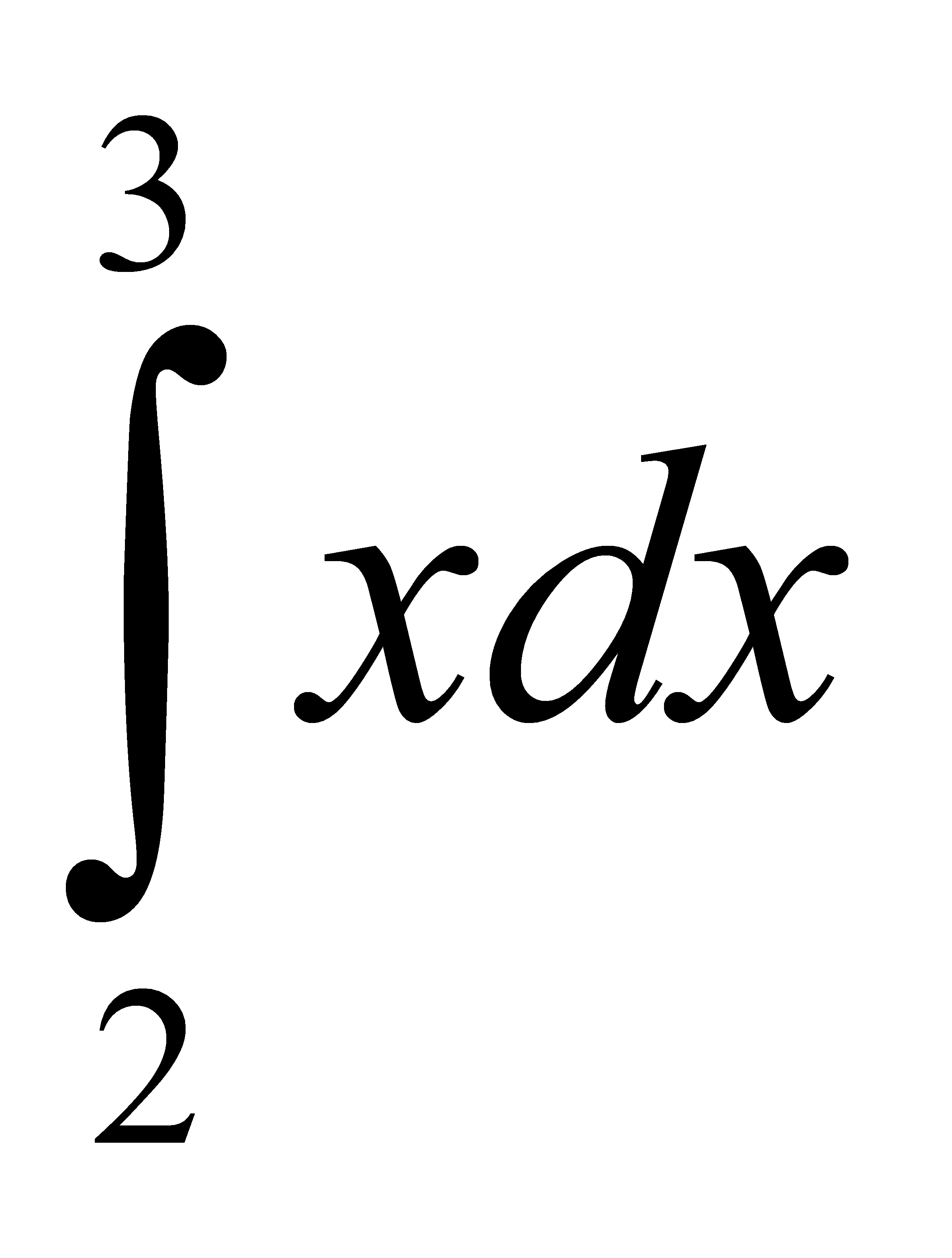 A) 2,5 C) 25/10 H) 5/2
A) 2,5 C) 25/10 H) 5/2
Есепте: 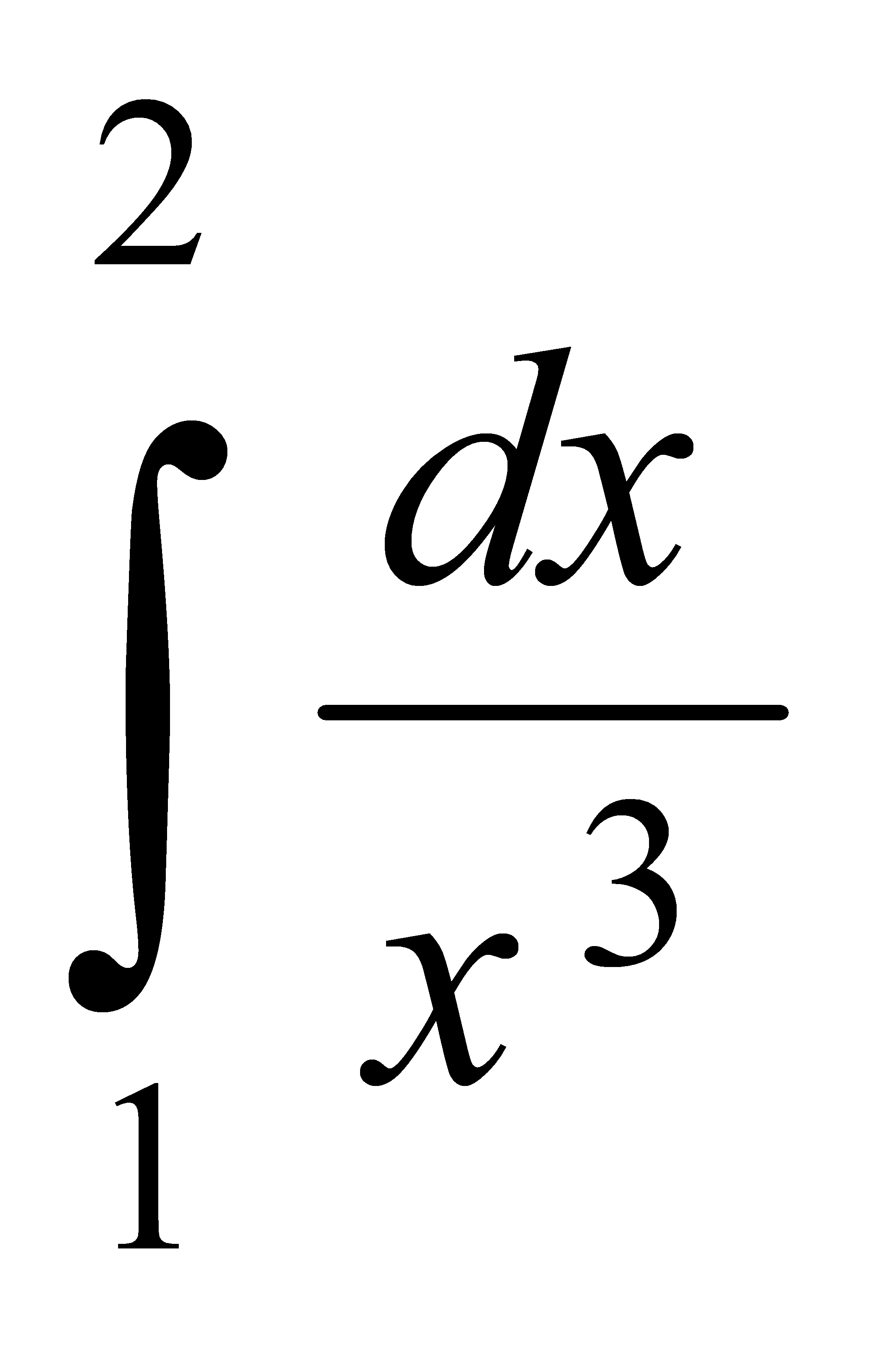 A) 3/8 C) 6/16 E) 9/24
A) 3/8 C) 6/16 E) 9/24
Есепте: 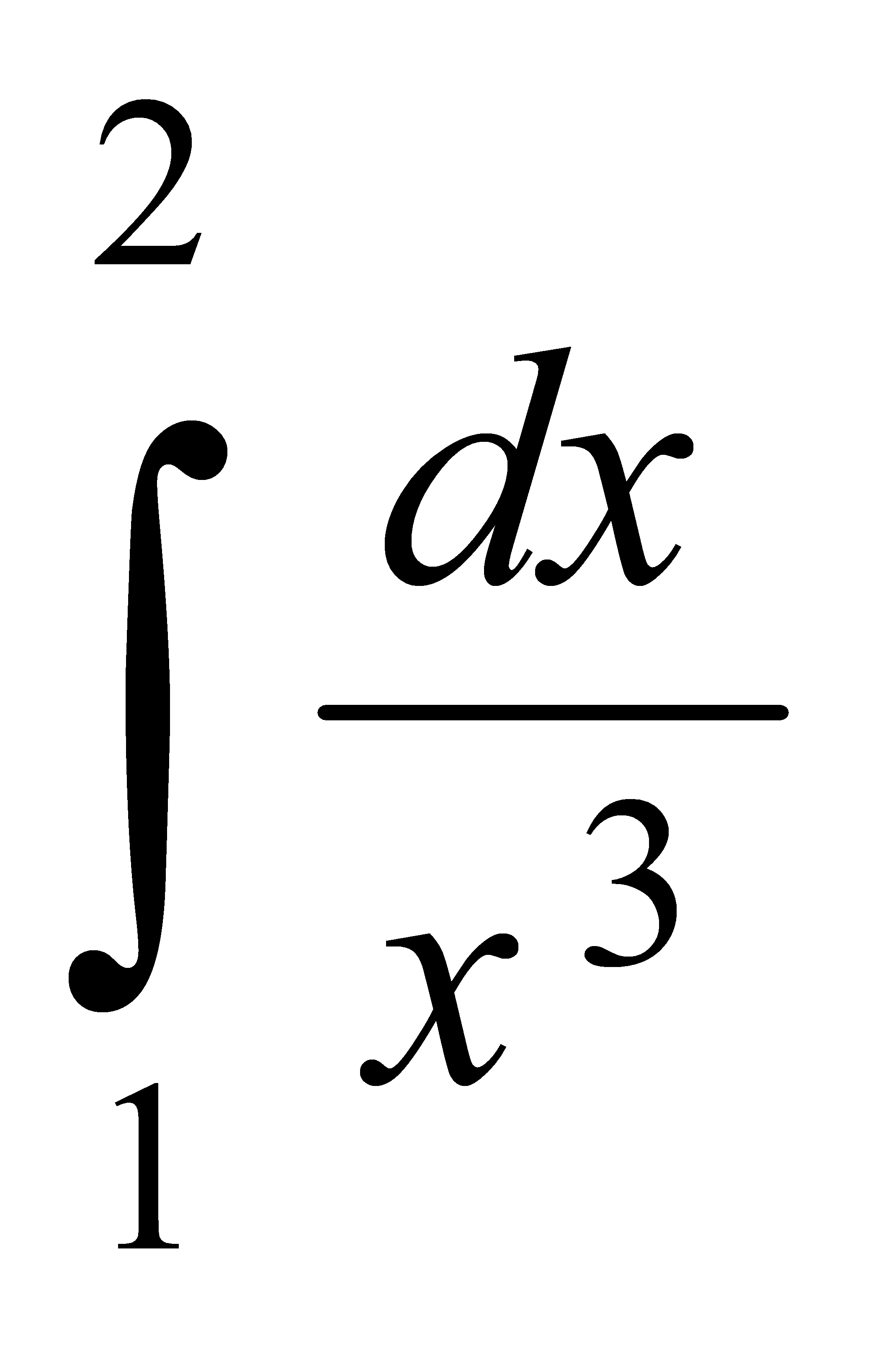 A) 3/8 C) 6/16 E) 9/24
A) 3/8 C) 6/16 E) 9/24
Есепте: 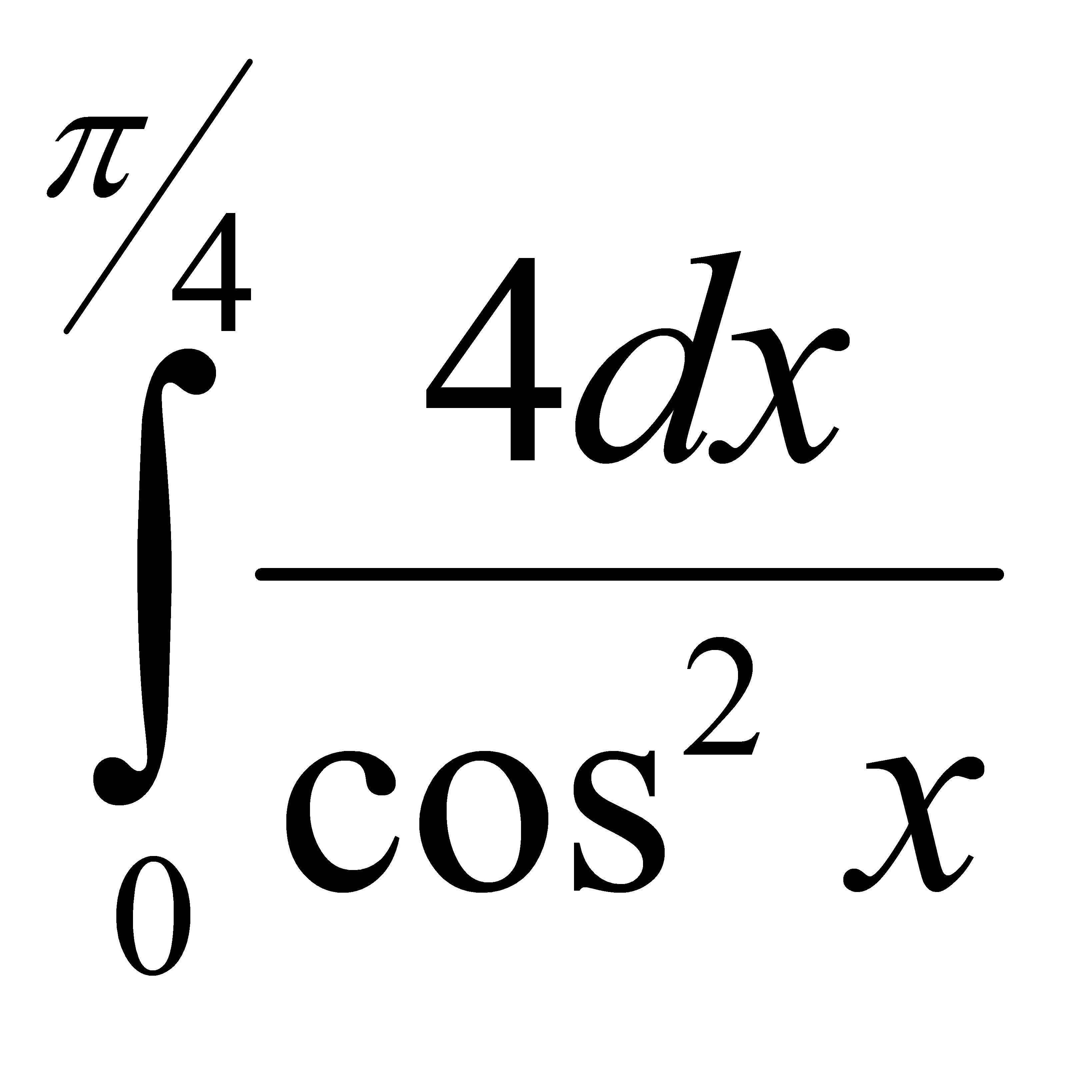 A) 4 G) 8/2 H) 12/3
A) 4 G) 8/2 H) 12/3
Есепте: 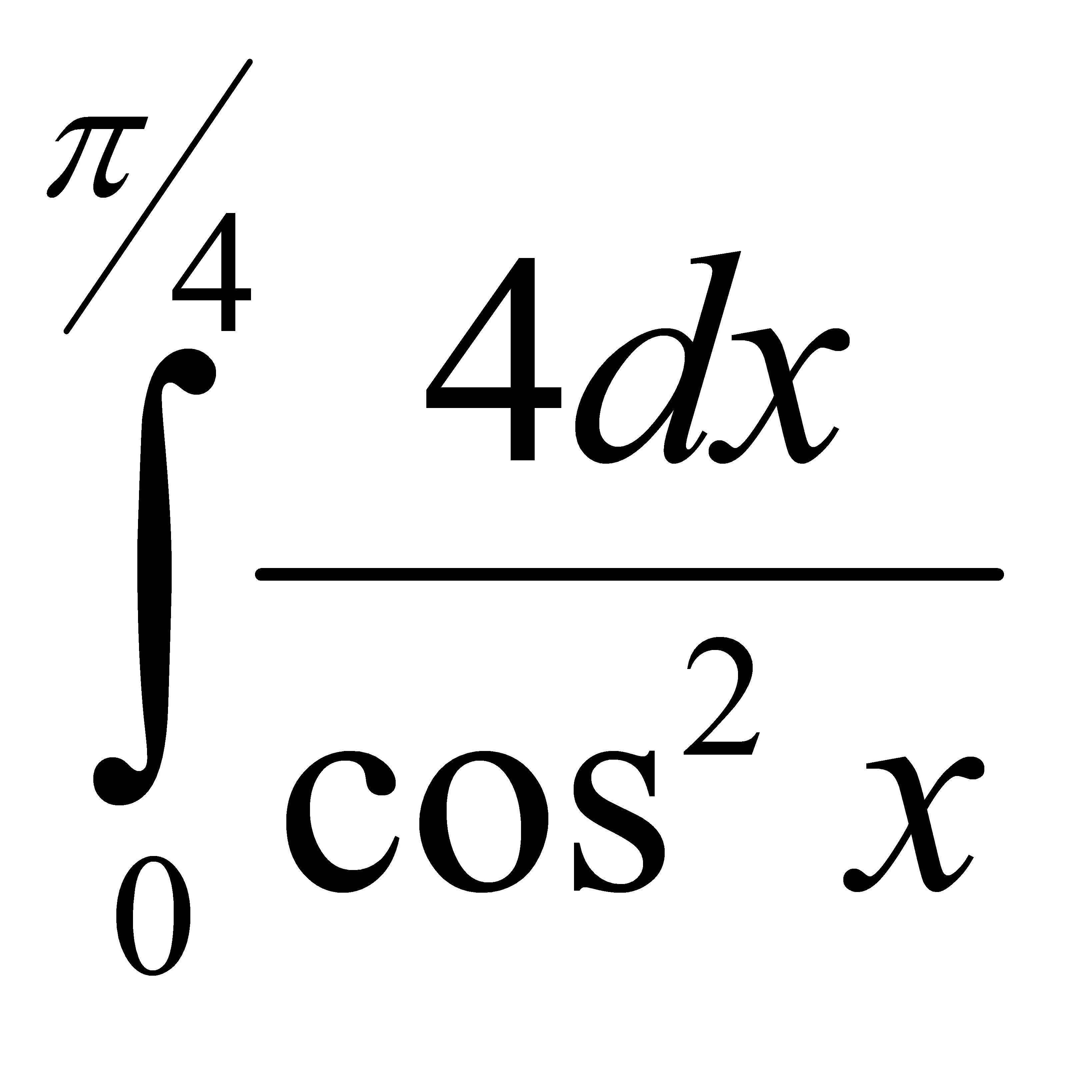 A) 4 G) 8/2 H) 12/3
A) 4 G) 8/2 H) 12/3
Есепте: 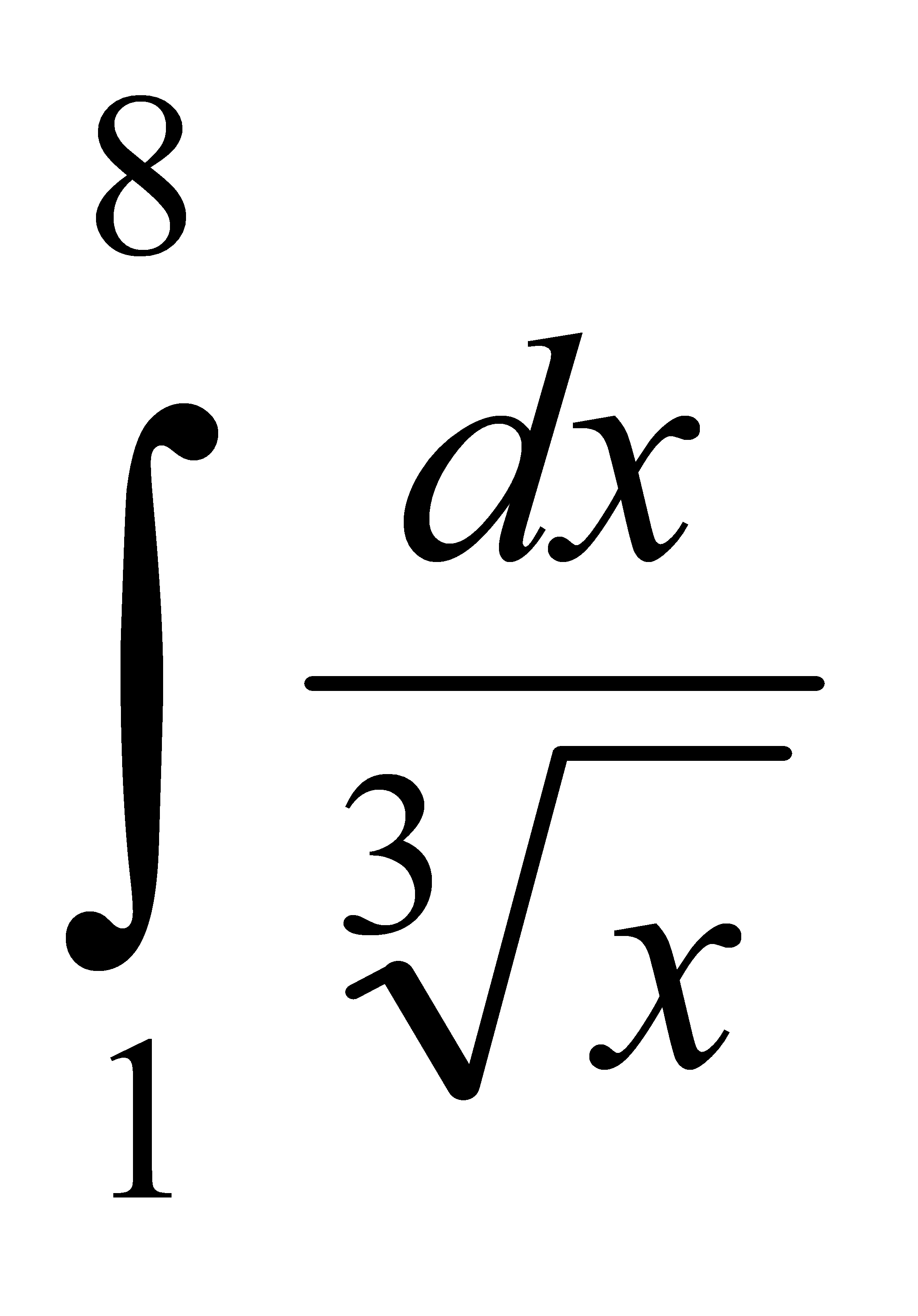 A) 4,5 D) 45 10-1 G) 9/2
A) 4,5 D) 45 10-1 G) 9/2
Есепте: 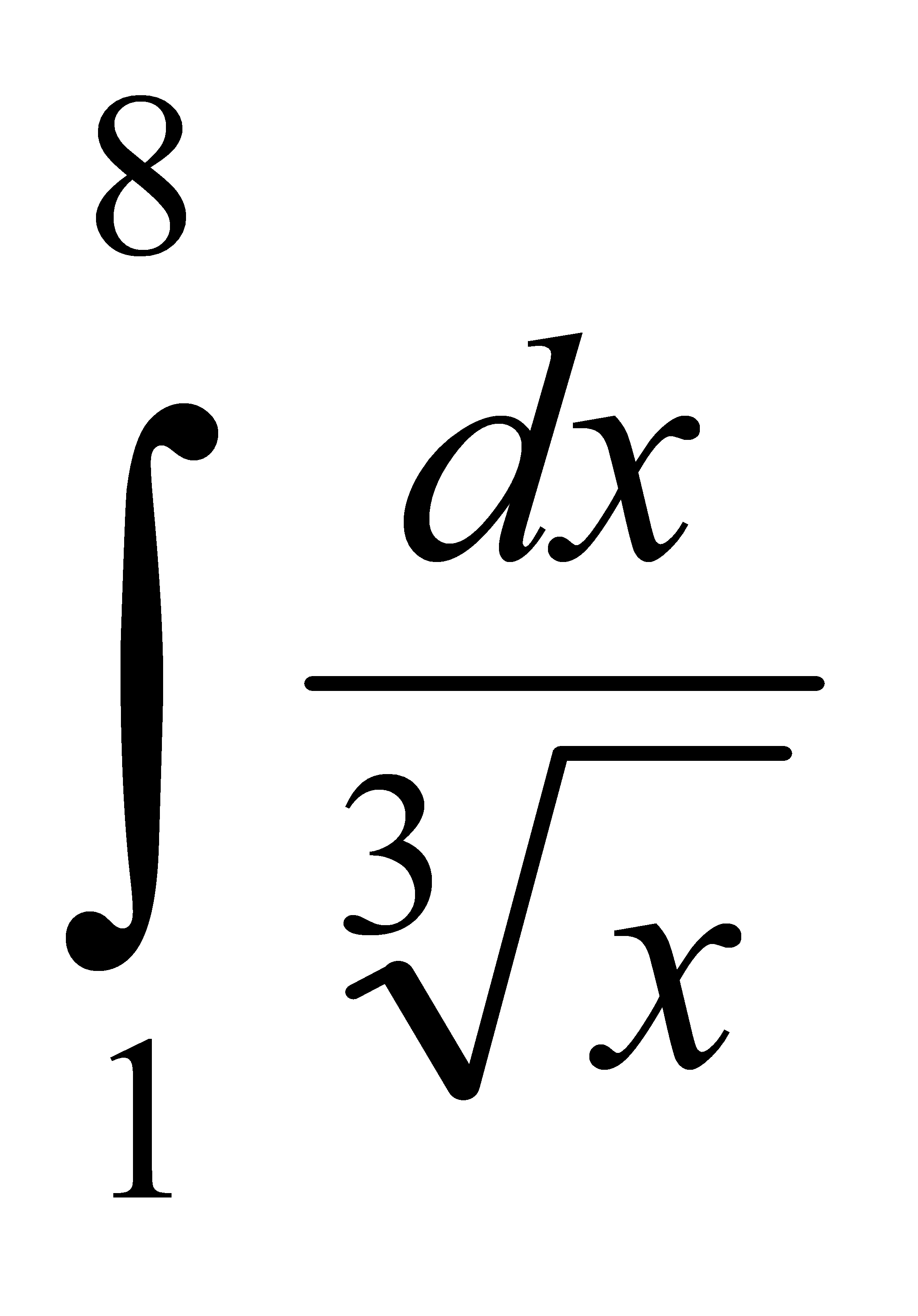 A) 4,5 D) 45 10-1 G) 9/2
A) 4,5 D) 45 10-1 G) 9/2
Есепте: 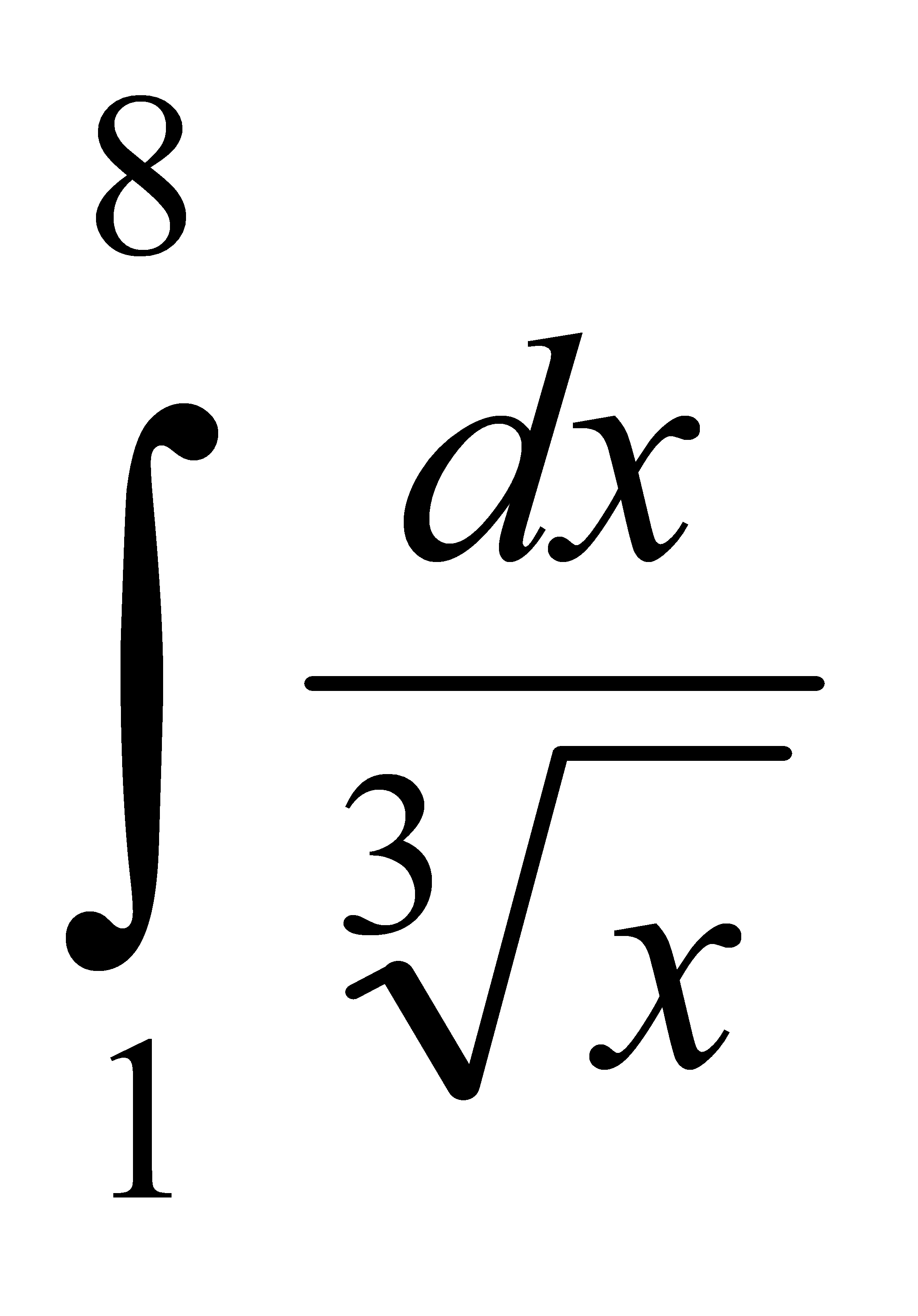 A) 4,5 G) 45/10 H) 9/2
A) 4,5 G) 45/10 H) 9/2
Есепте: 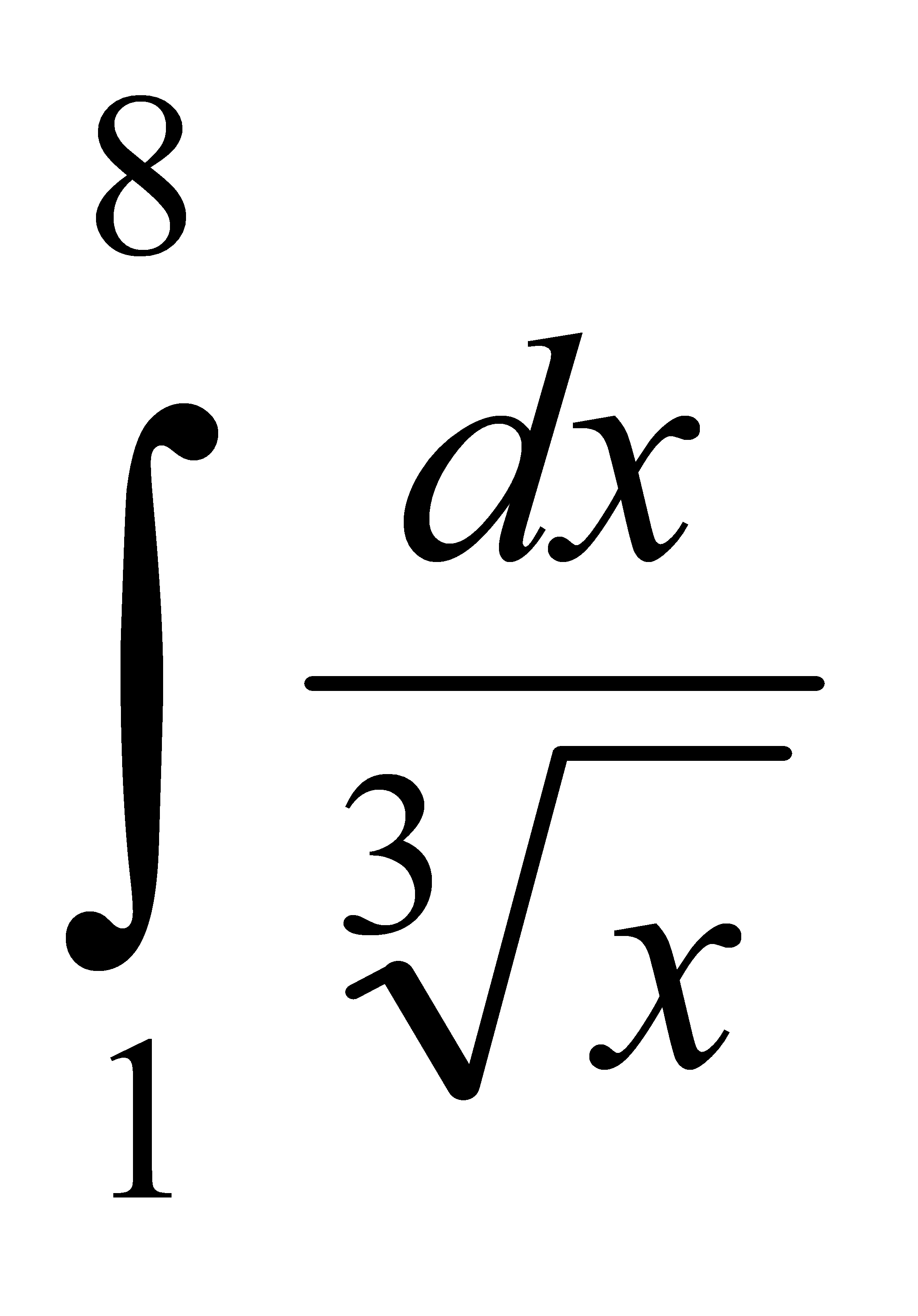 A) 4,5 G) 45/10 H) 9/2
A) 4,5 G) 45/10 H) 9/2
Есепте: 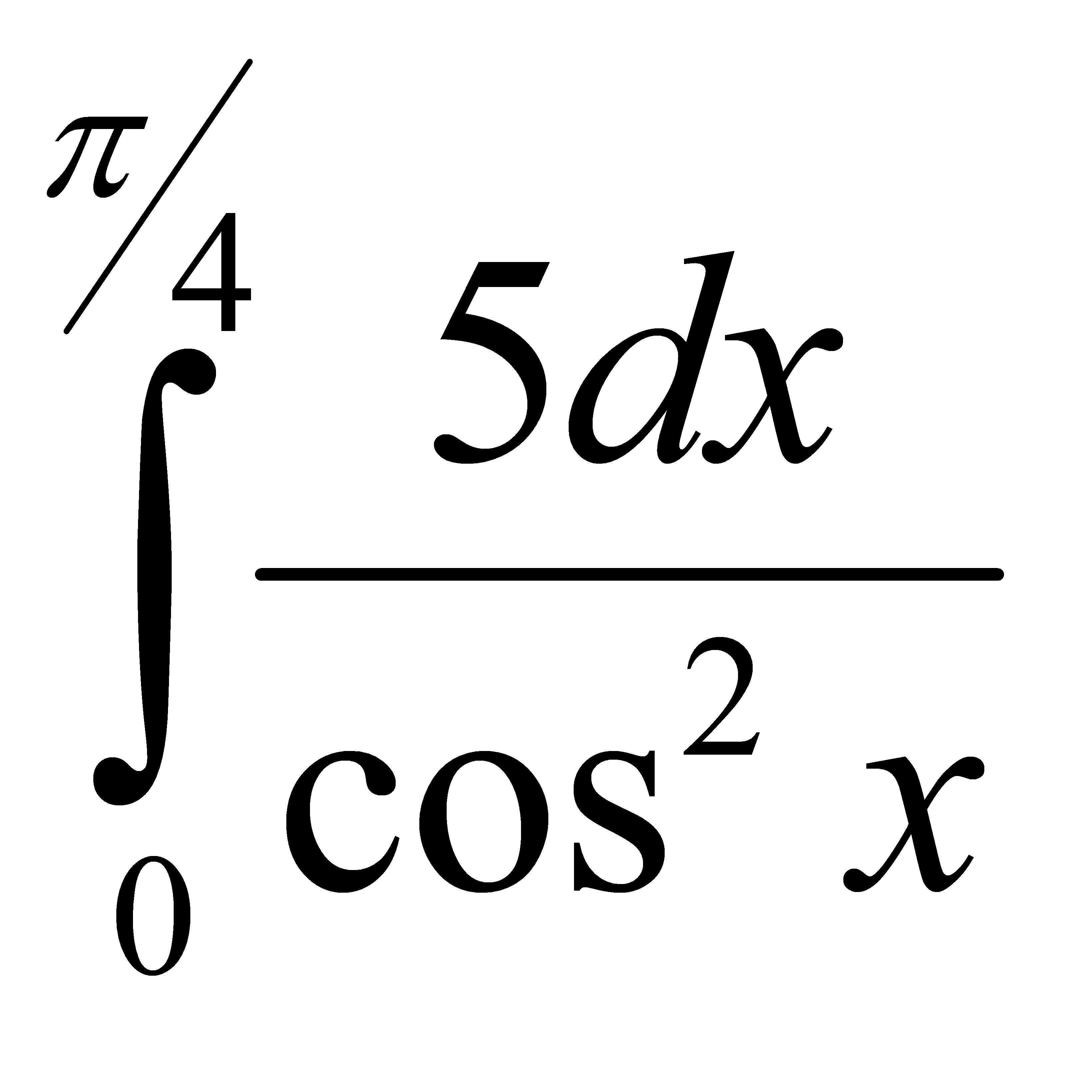 A) 5 B) 10/2 C) 15/3
A) 5 B) 10/2 C) 15/3
Есепте: 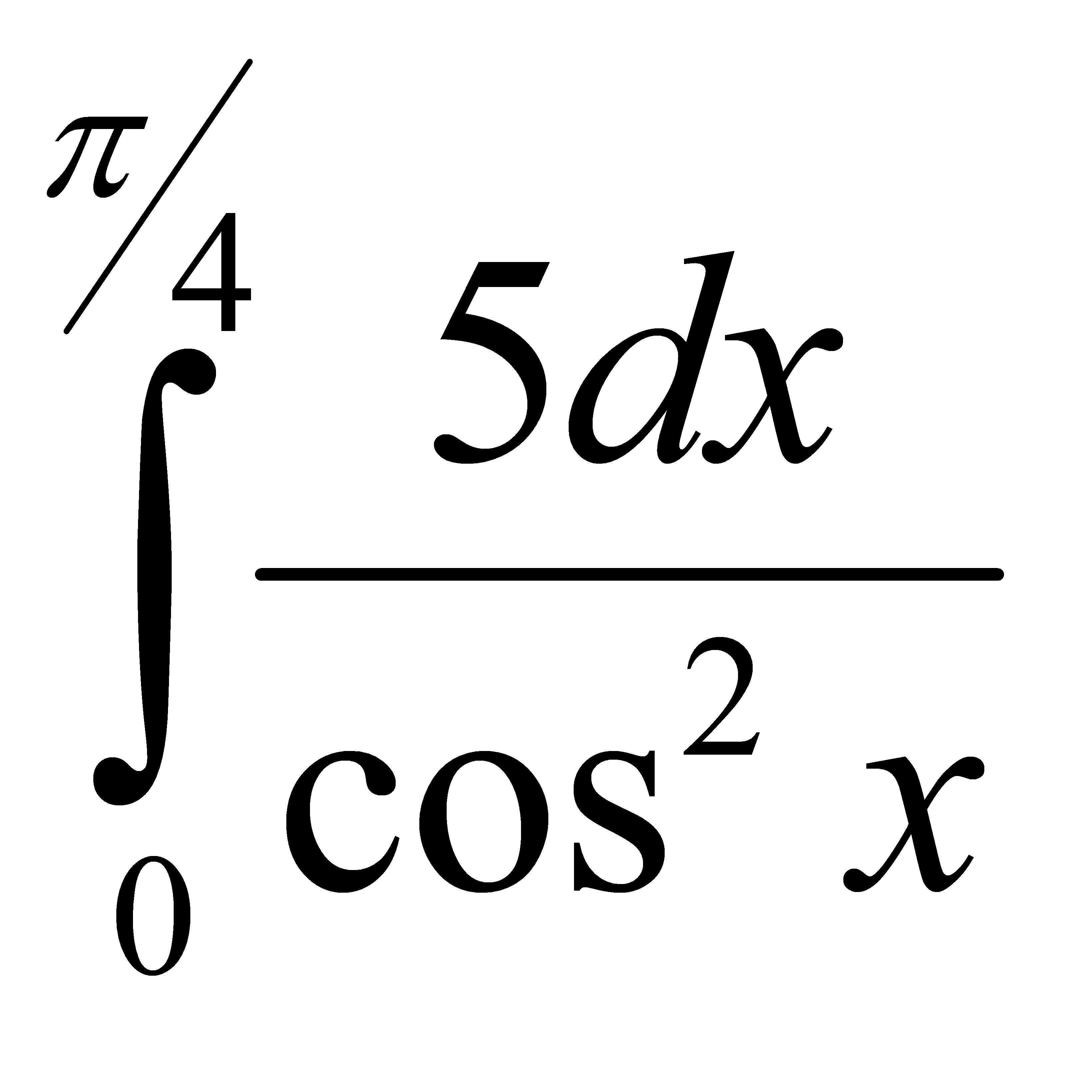 A) 5 B) 10/2 C) 15/3
A) 5 B) 10/2 C) 15/3
Есепте: 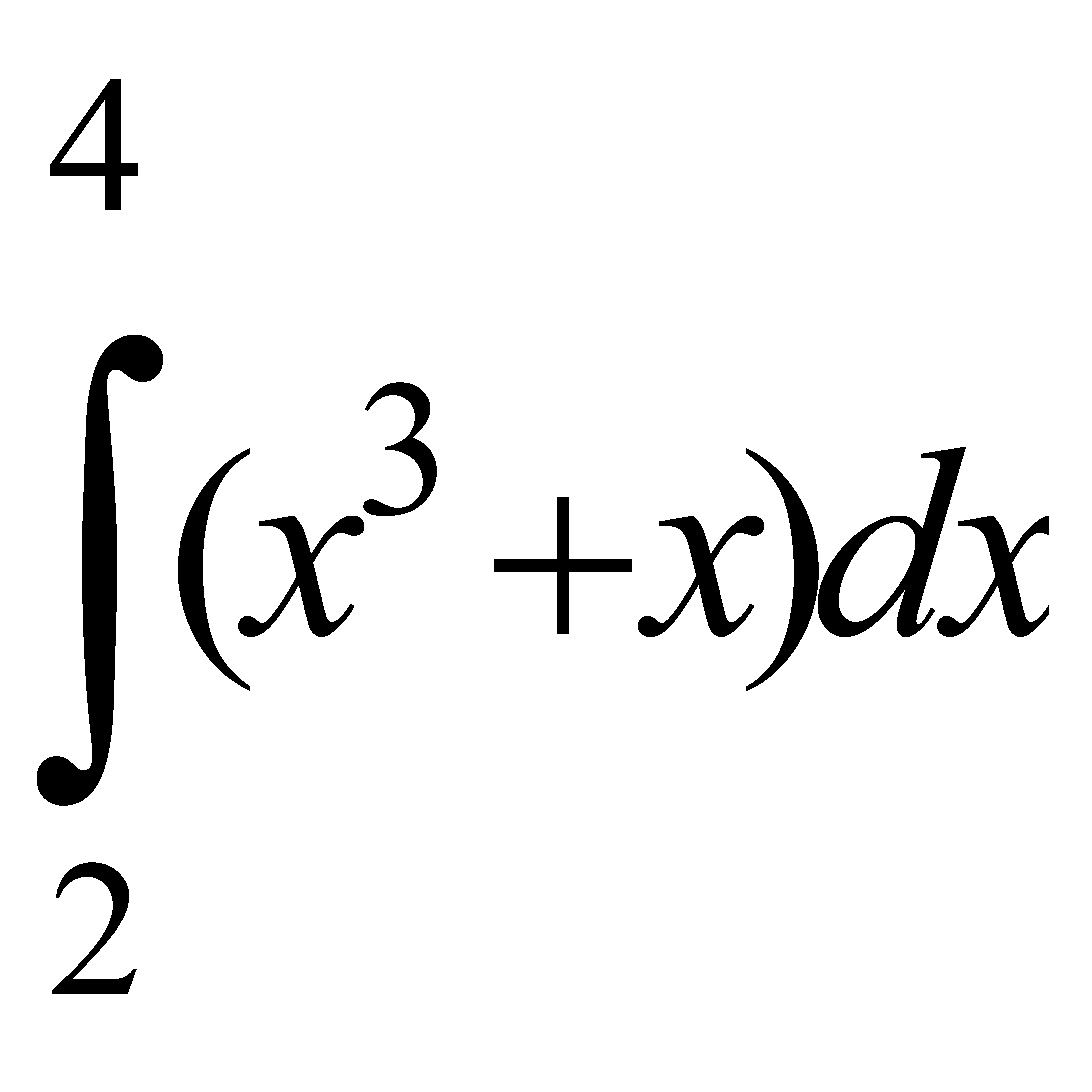 A) 66 D) 132/2 G) 198/3
A) 66 D) 132/2 G) 198/3
Есепте: 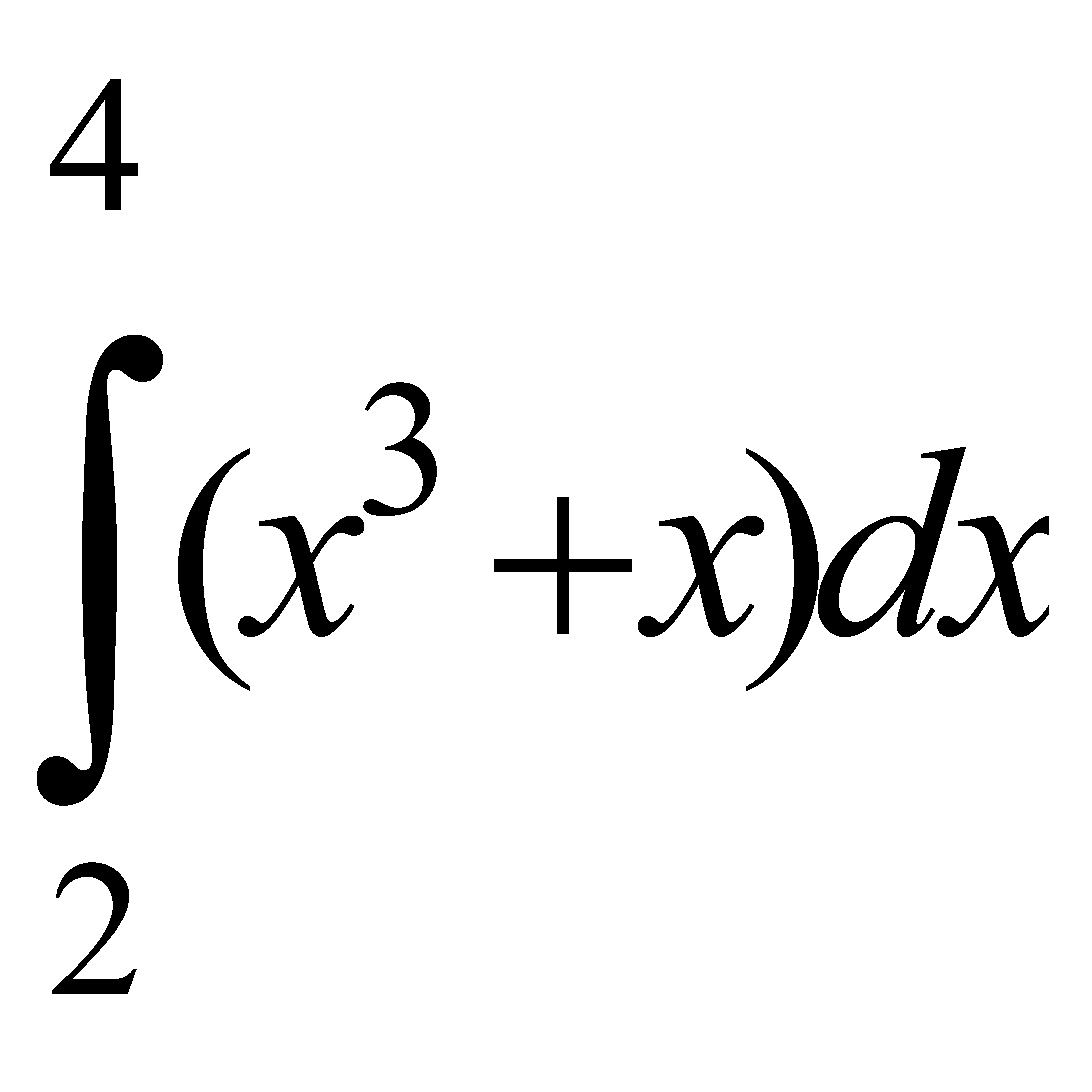 A) 66 D) 132/2 G) 198/3
A) 66 D) 132/2 G) 198/3
Есепте: 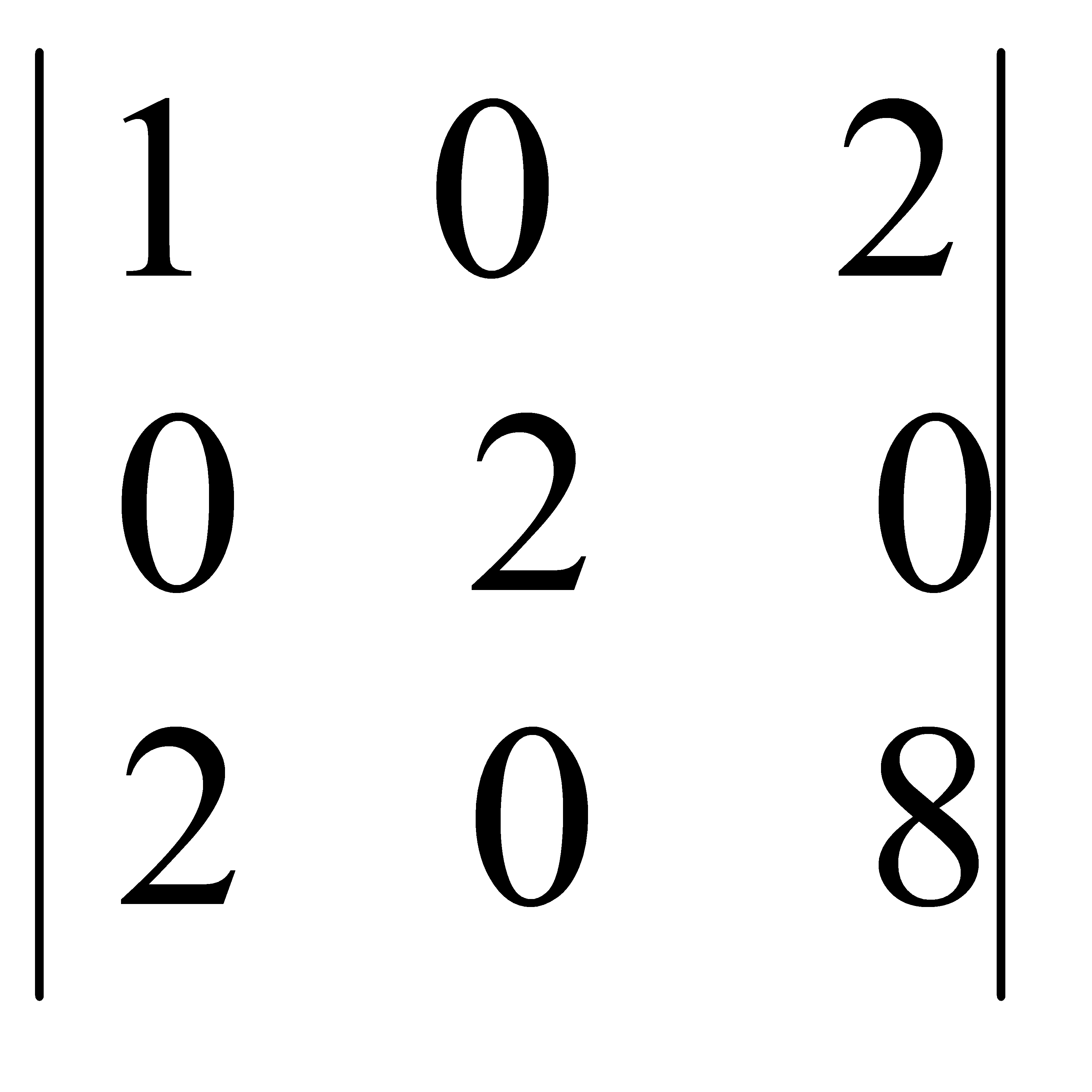 A) 8 C) 16/2 E) 24/3
A) 8 C) 16/2 E) 24/3
Есепте: 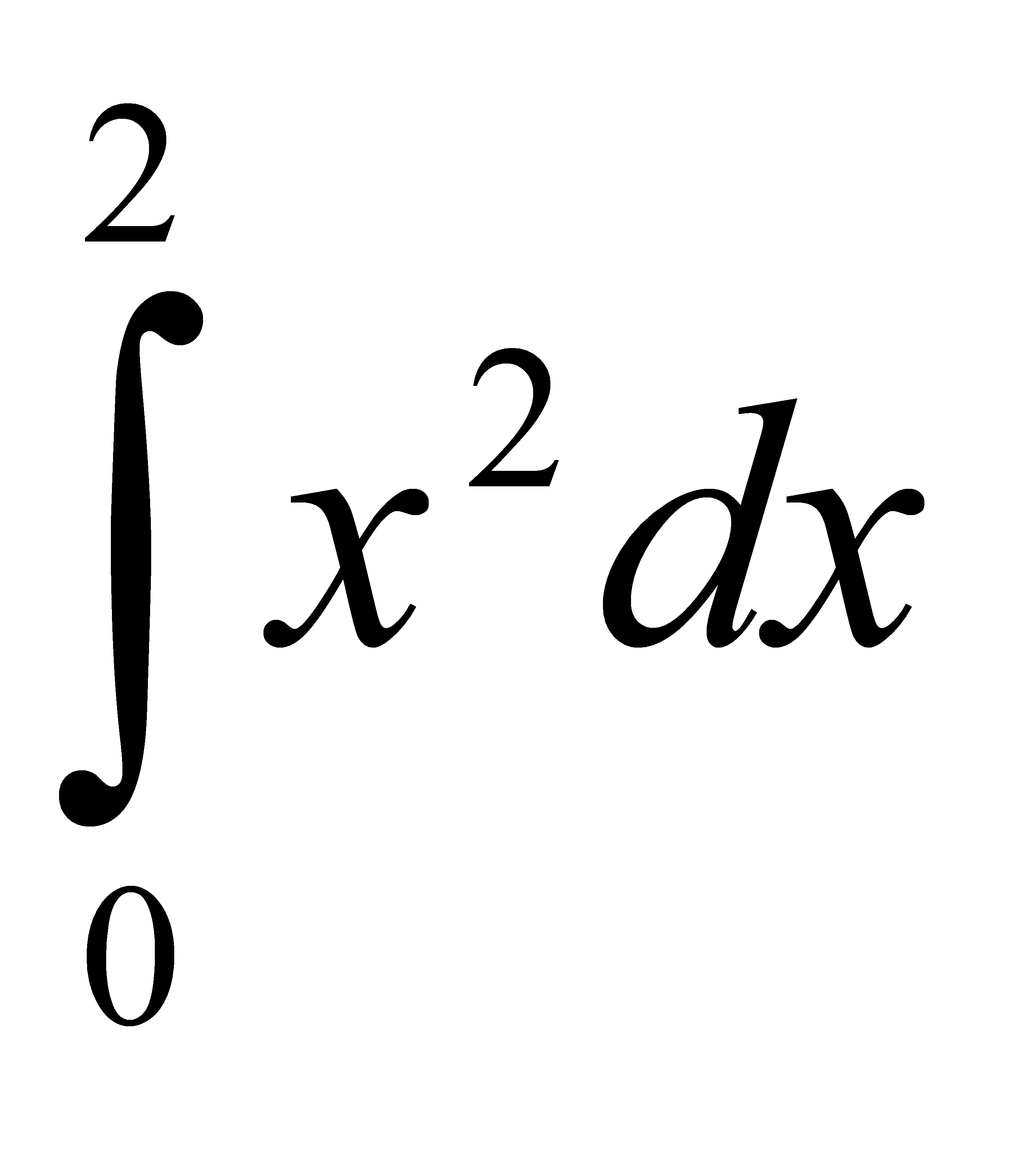 A) 8/3 G) 16/6 H) 24/9
A) 8/3 G) 16/6 H) 24/9
Есепте: 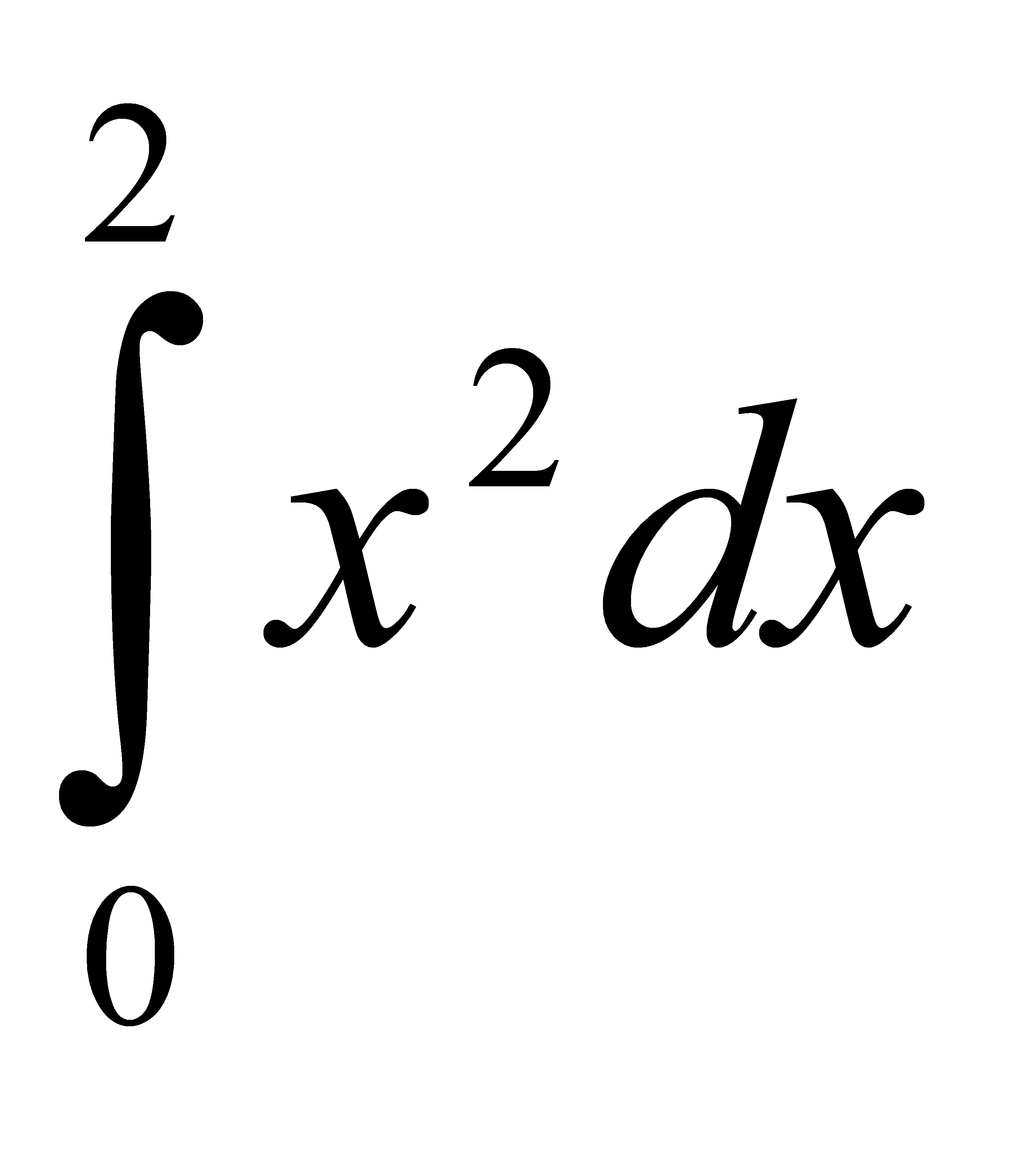 A) 8/3 G) 16/6 H) 24/9
A) 8/3 G) 16/6 H) 24/9
Есепте: 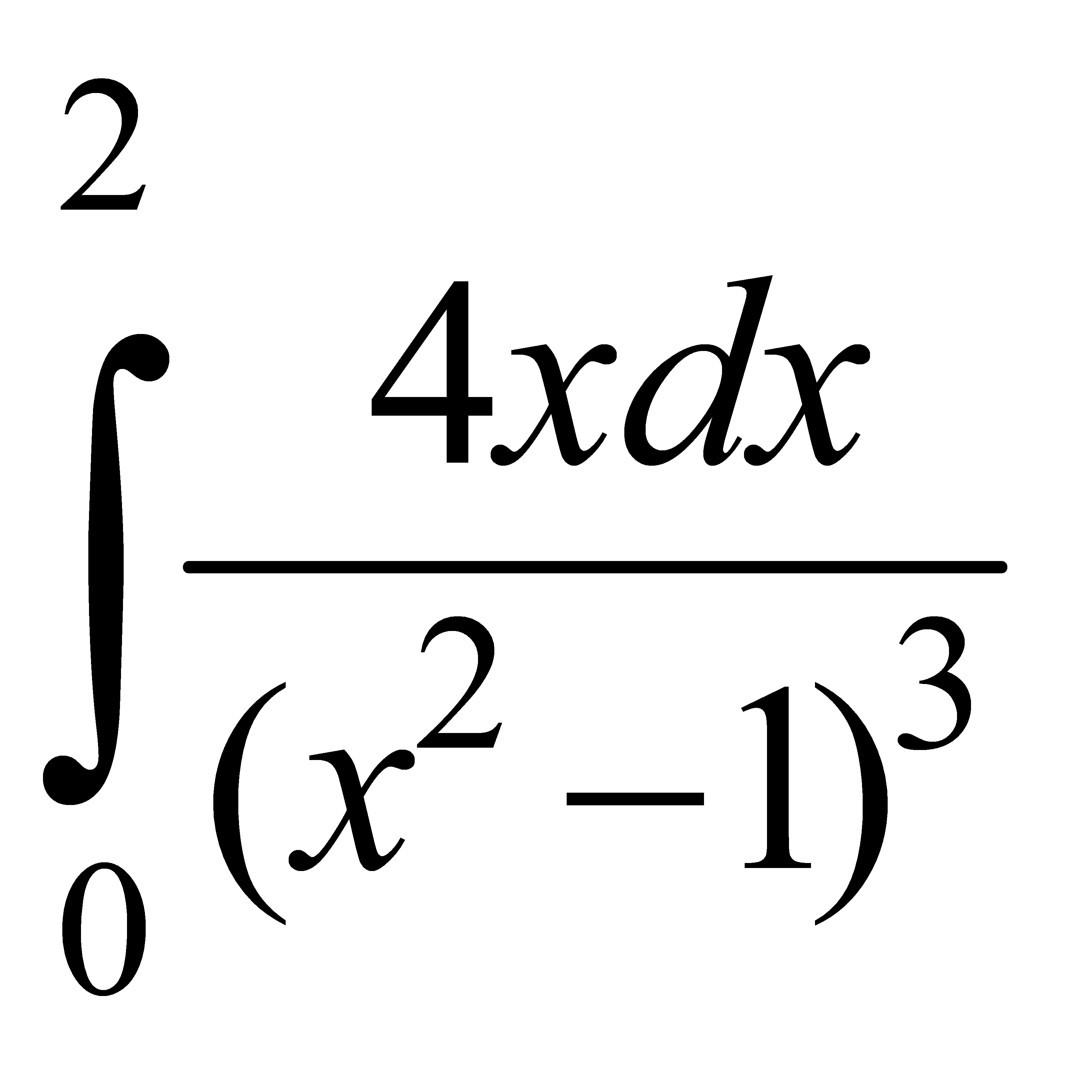 A) 8/9 B) 24/27 H) 16/18
A) 8/9 B) 24/27 H) 16/18
Есепте: 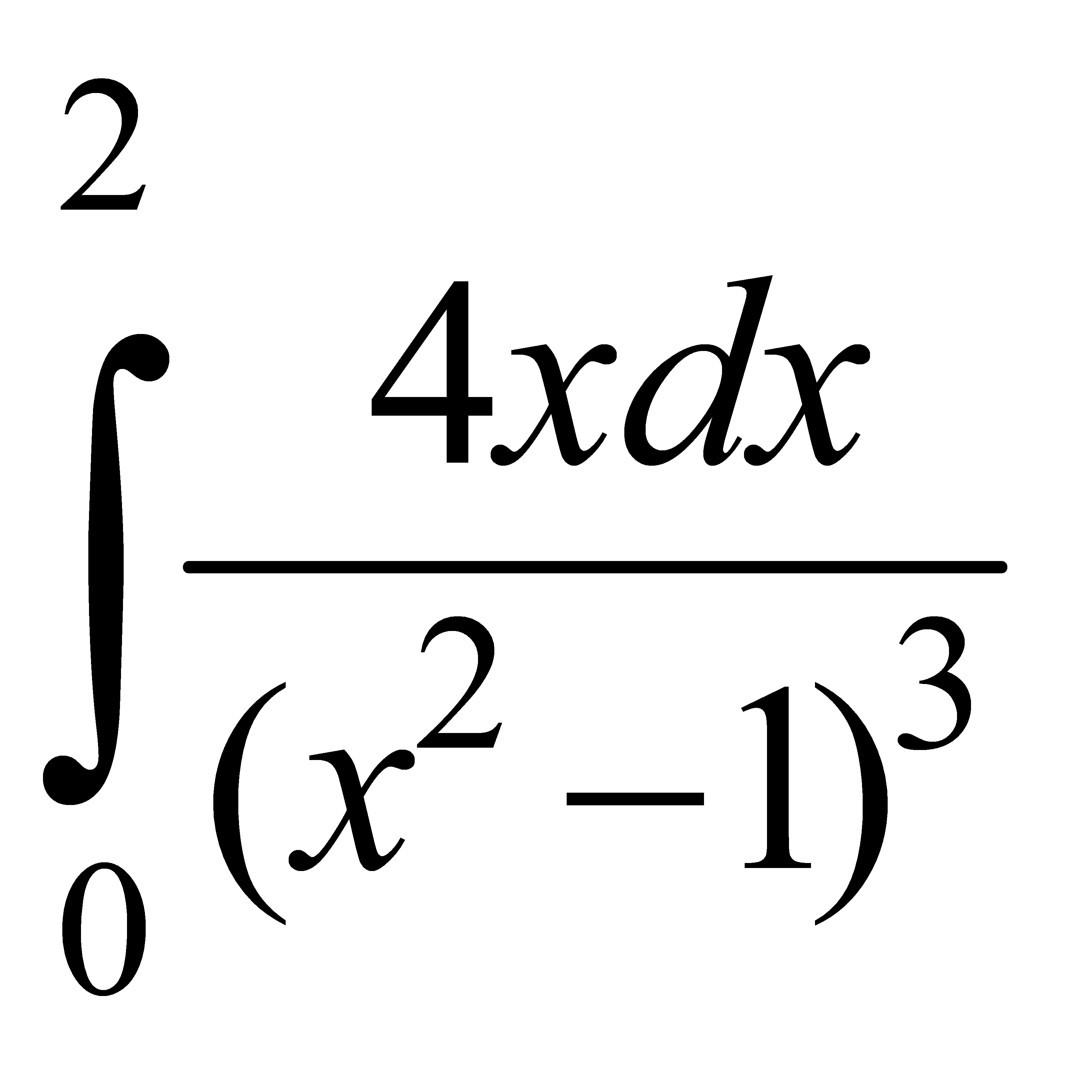 A) 8/9 B) 24/27 H) 16/18
A) 8/9 B) 24/27 H) 16/18
Есепте: 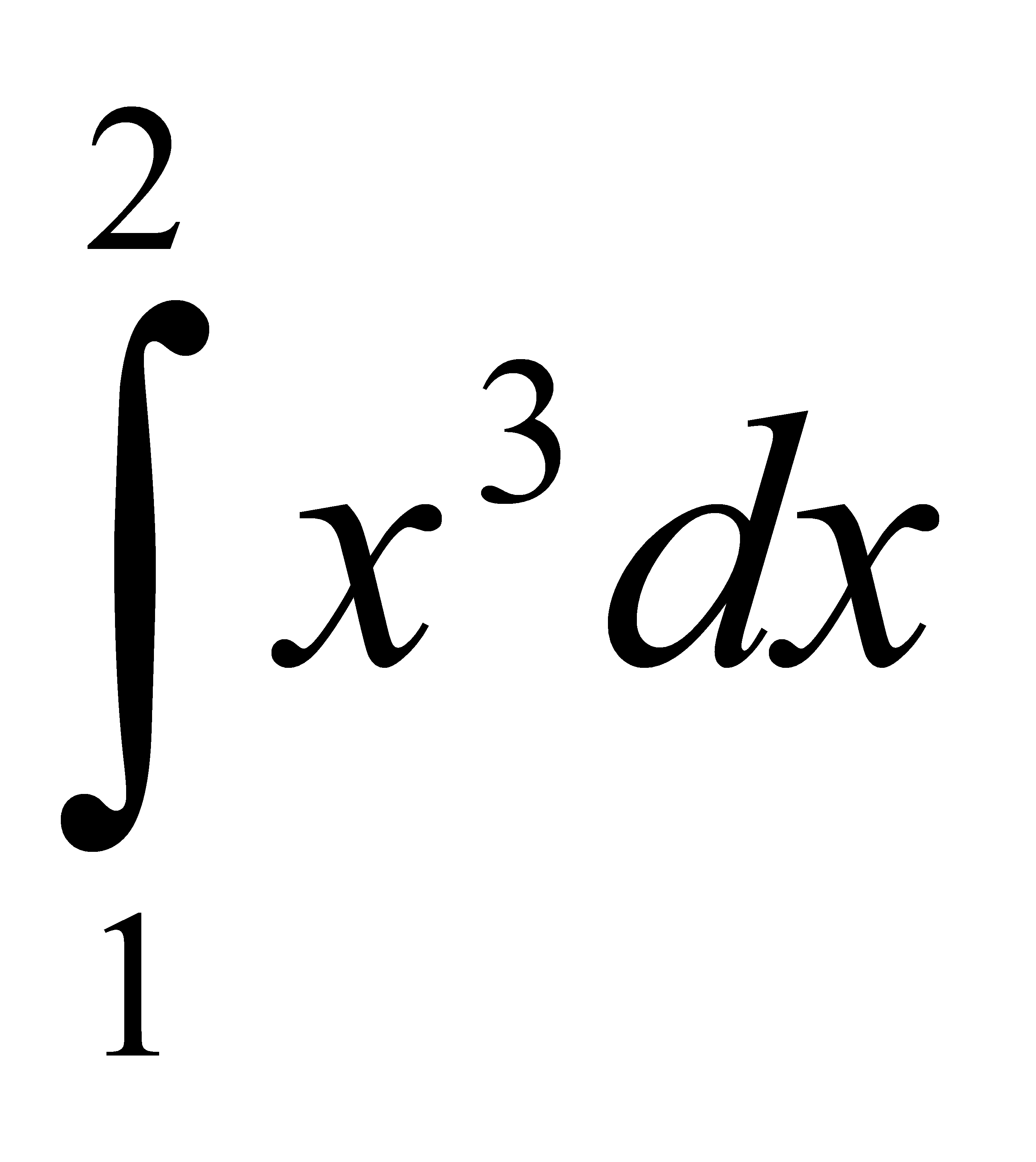 B) 15/4 D) 30/8 G) 45/12
B) 15/4 D) 30/8 G) 45/12
Есепте: 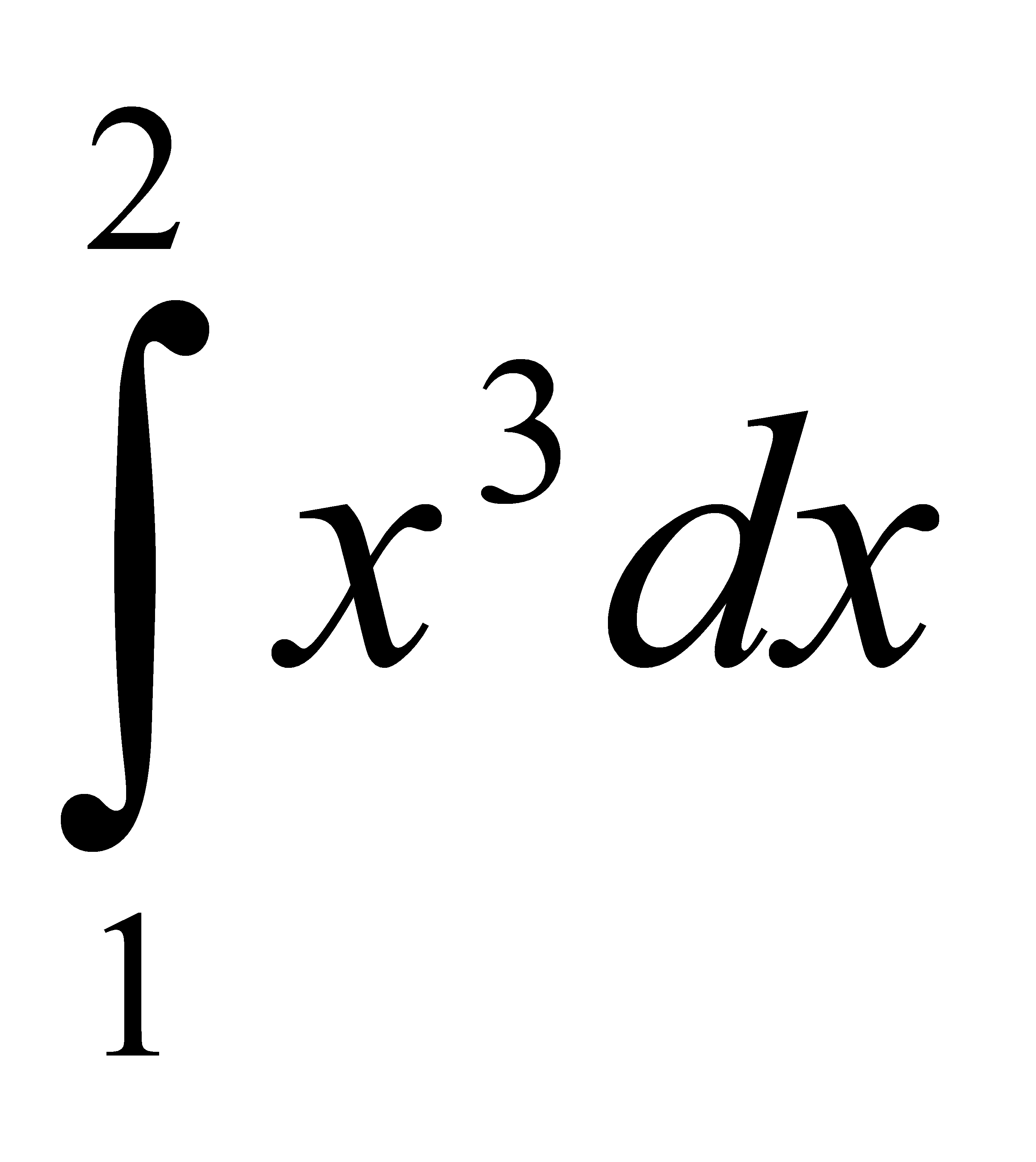 B) 15/4 D) 30/8 G) 45/12
B) 15/4 D) 30/8 G) 45/12
Есепте: 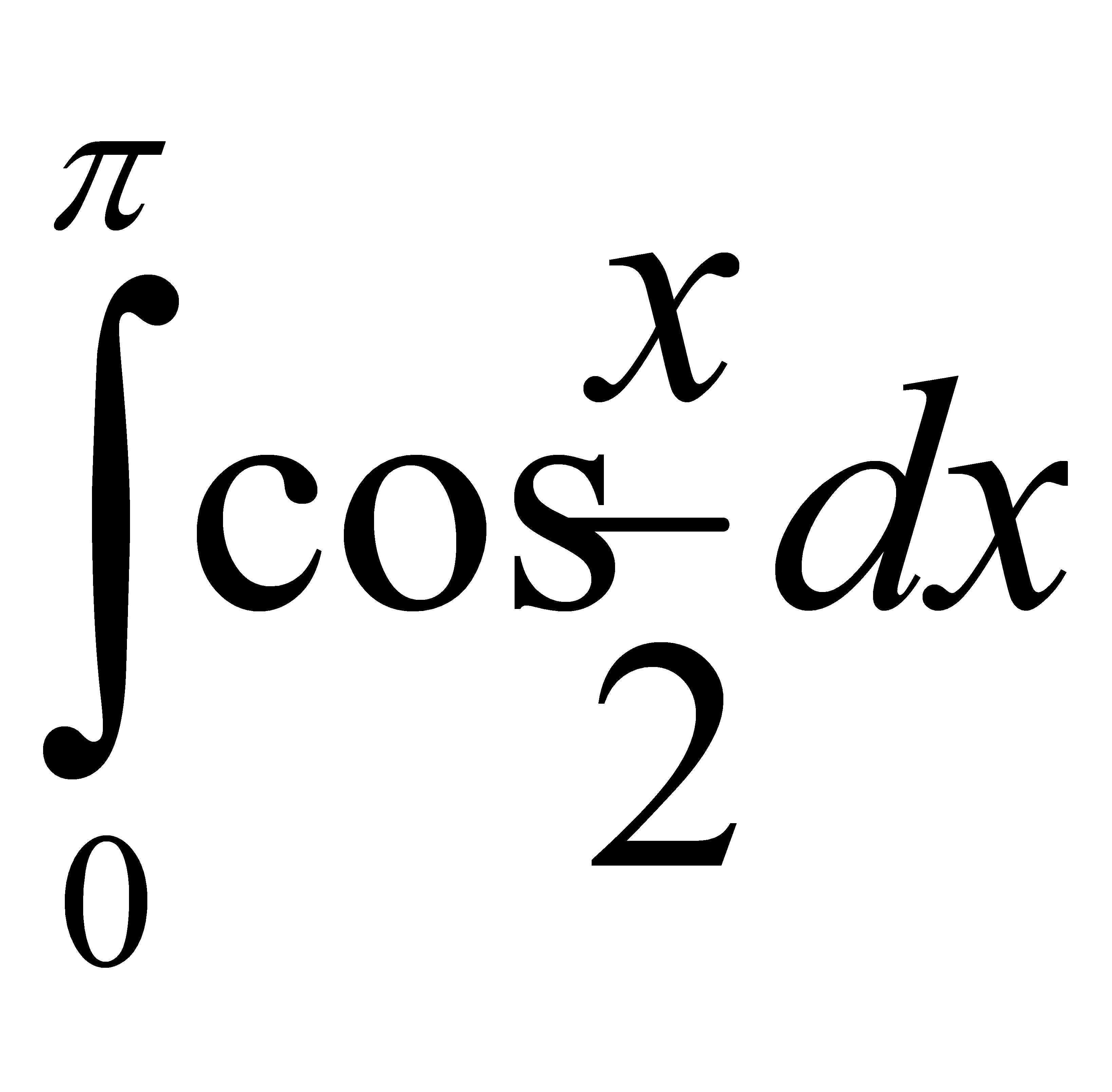 C) 2 E) 4/2 H) 6/3
C) 2 E) 4/2 H) 6/3
Есепте: 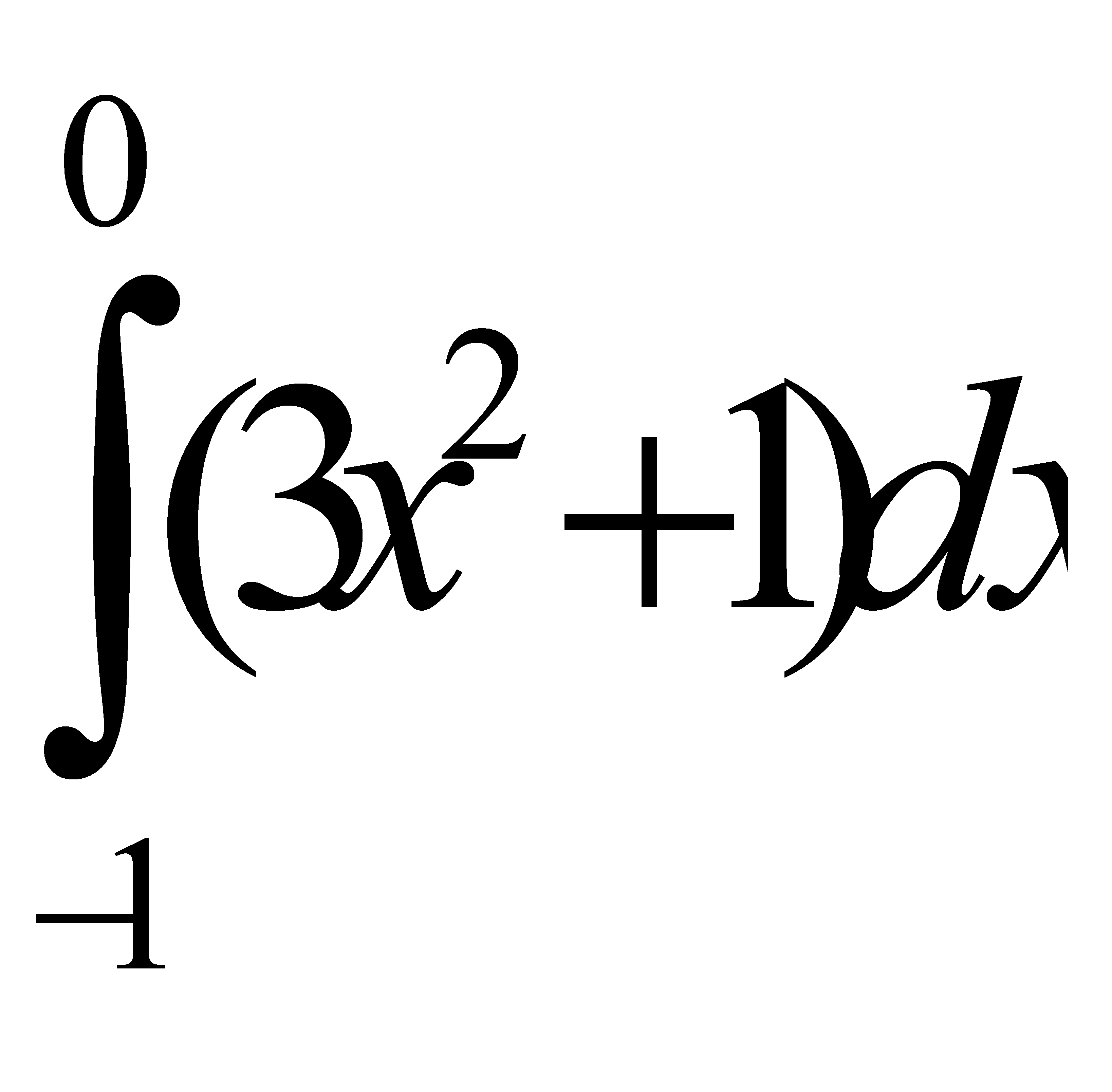 C) 2 E) 4/2 H) 6/3
C) 2 E) 4/2 H) 6/3
Есепте: 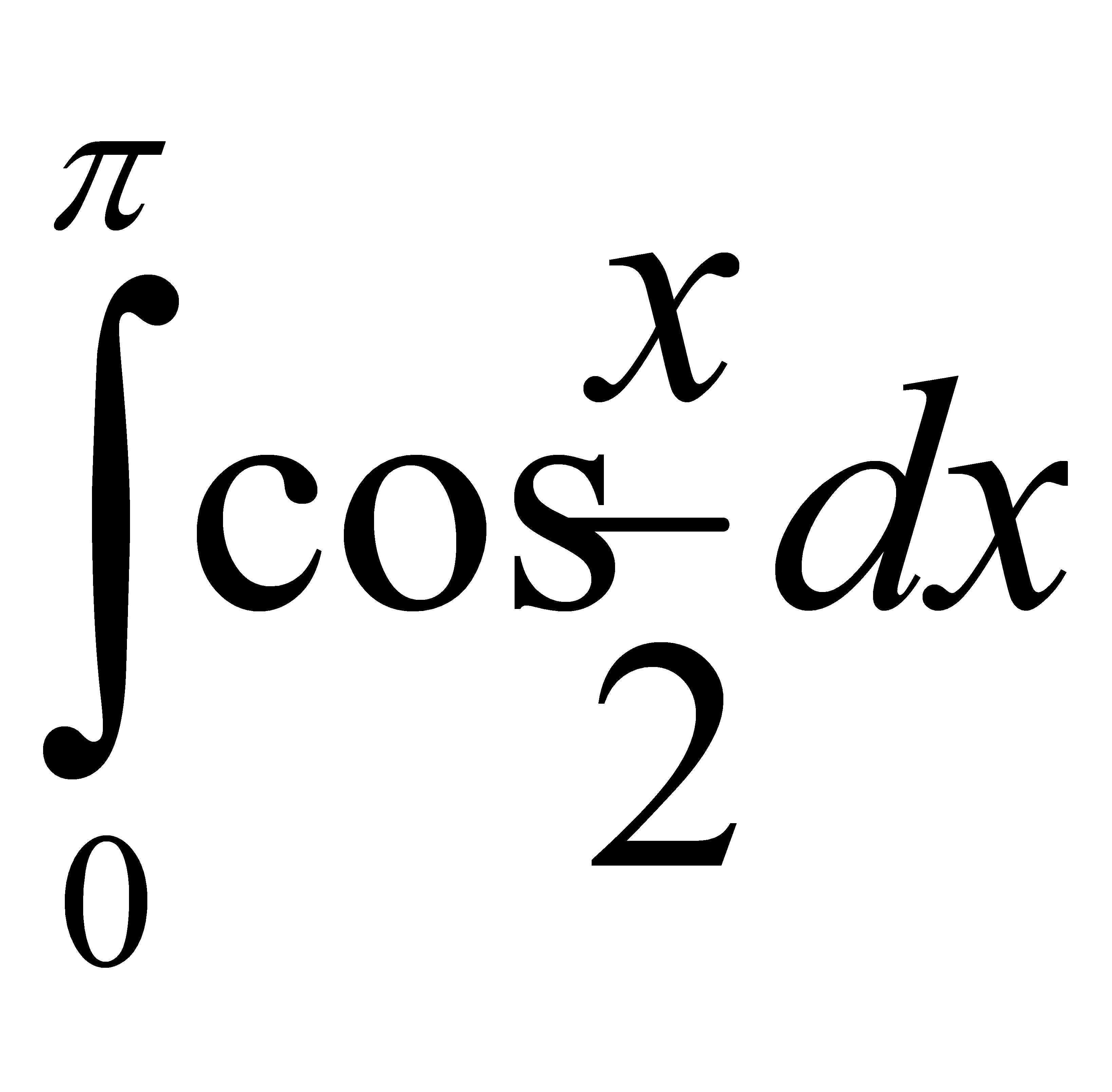 C) 2 E) 4/2 H) 6/3
C) 2 E) 4/2 H) 6/3
Есепте: 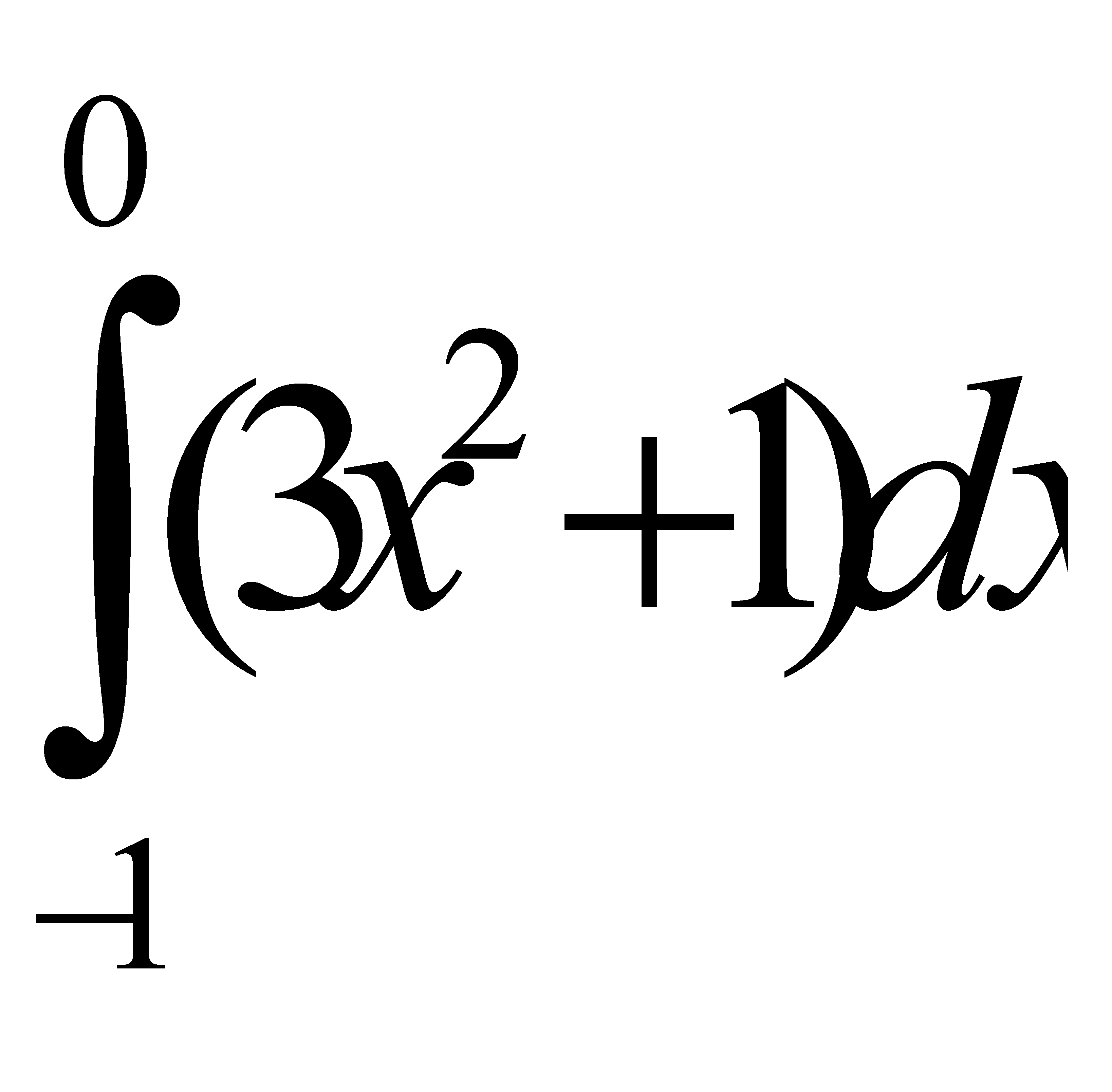 C) 2 E) 4/2 H) 6/3
C) 2 E) 4/2 H) 6/3
Есепте: 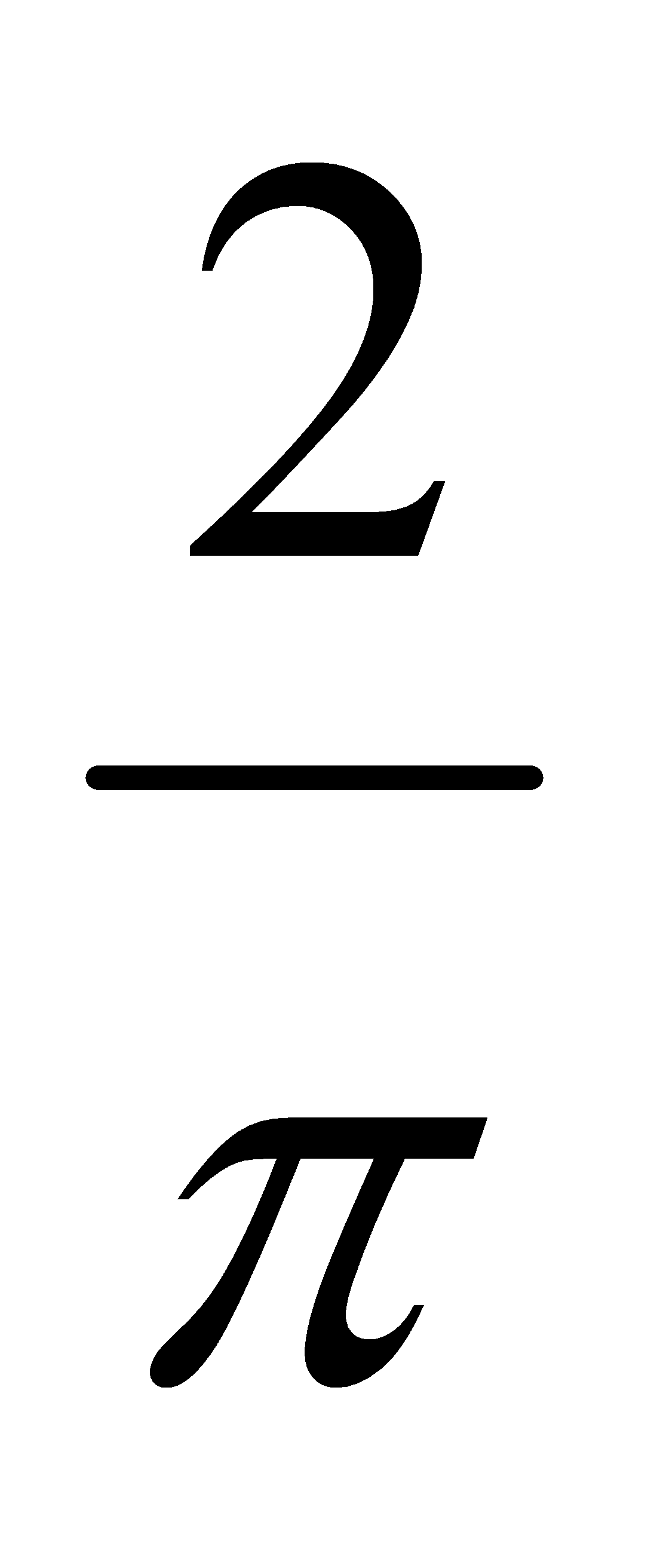
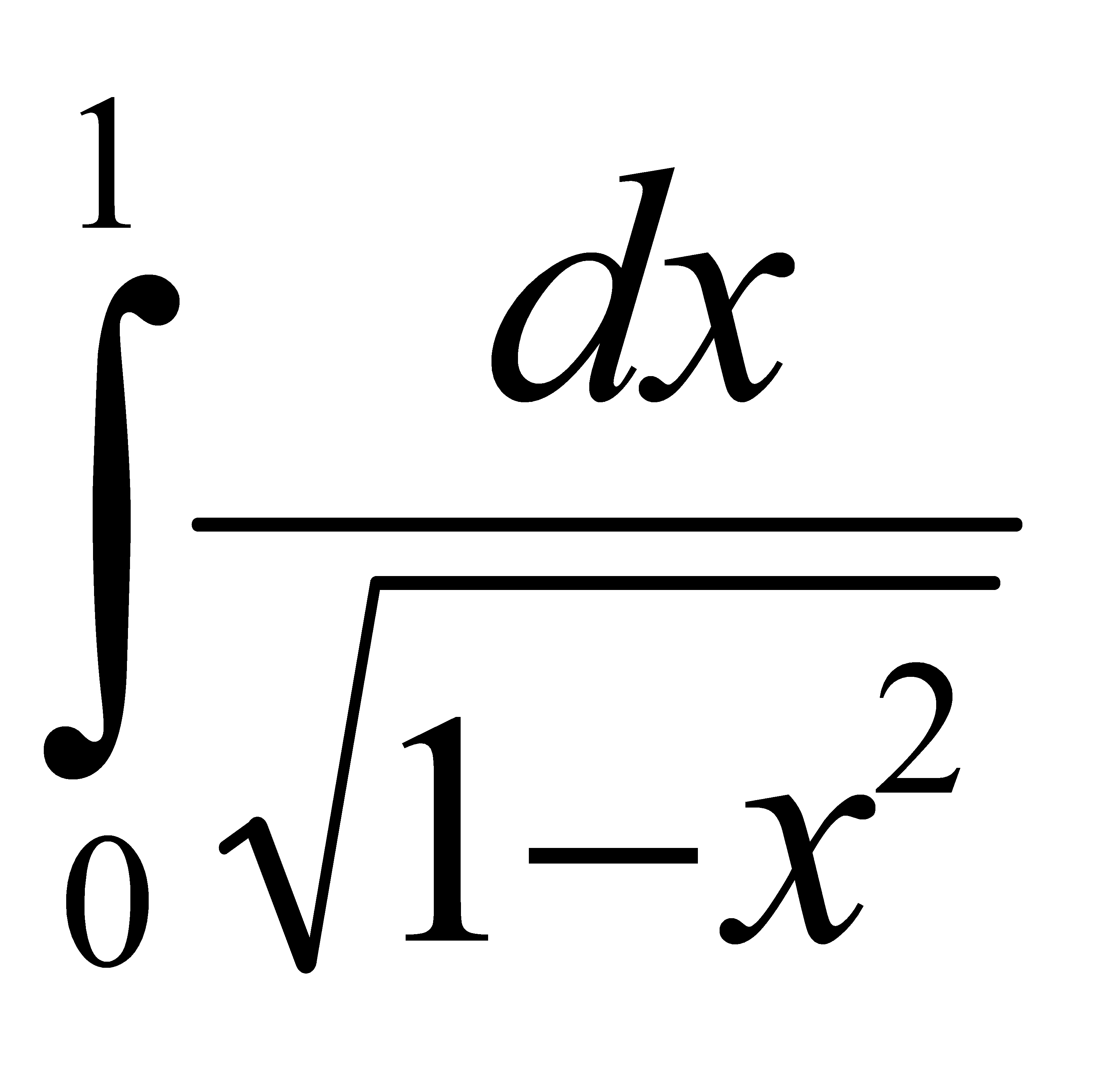 D) 1 G) 2/2 H) 8/8
D) 1 G) 2/2 H) 8/8
Есепте: 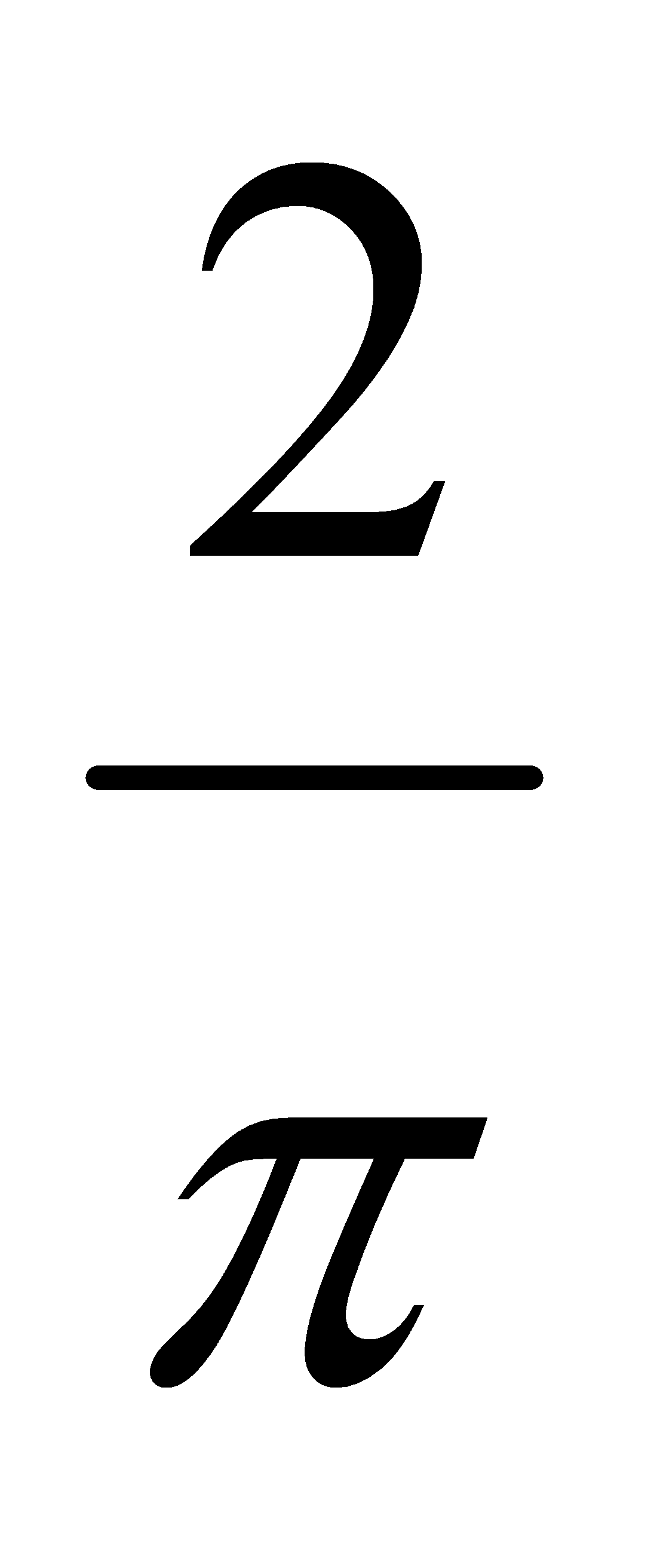
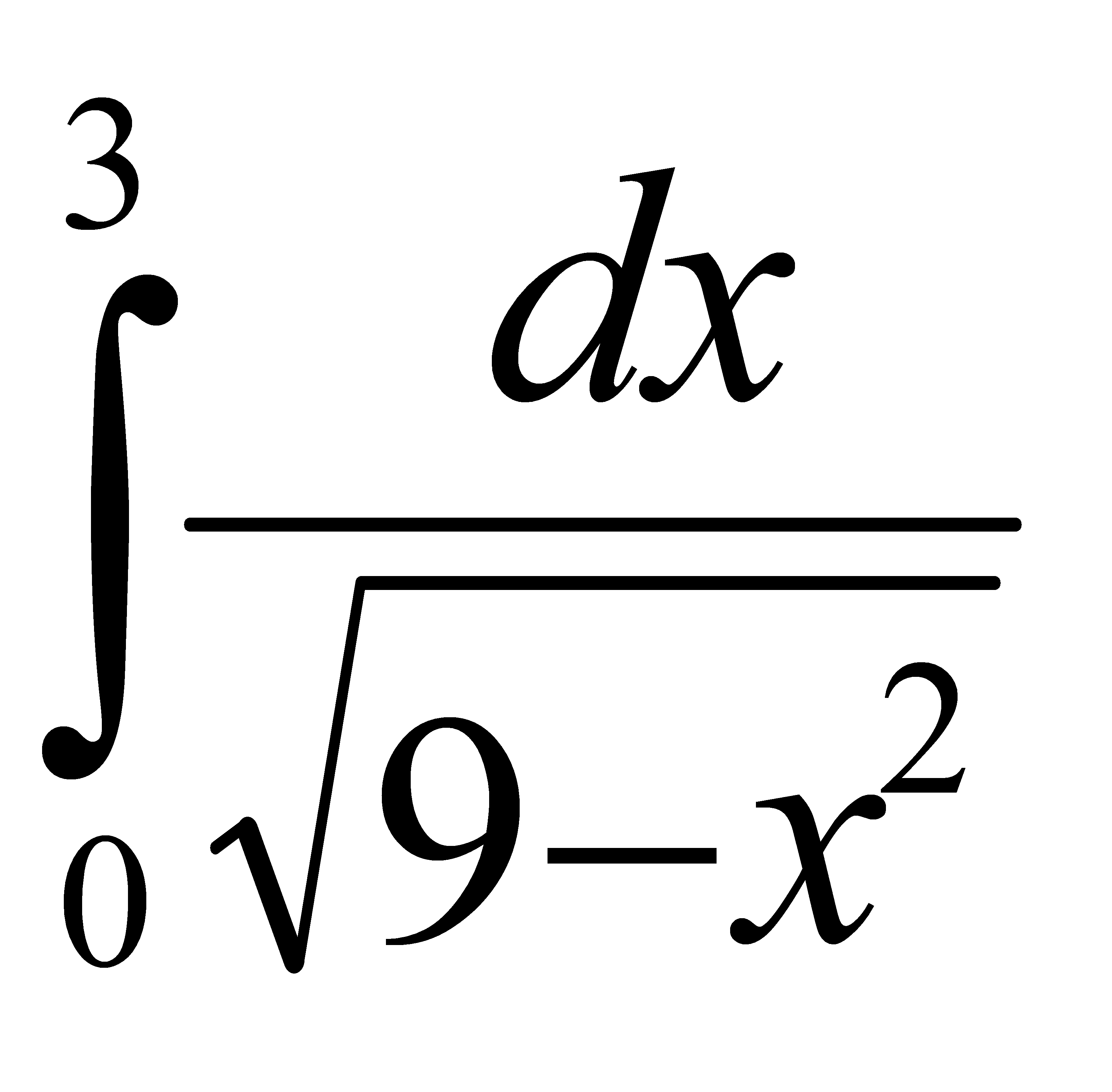 D) 1 G) 2/2 H) 8/8
D) 1 G) 2/2 H) 8/8
Есепте: 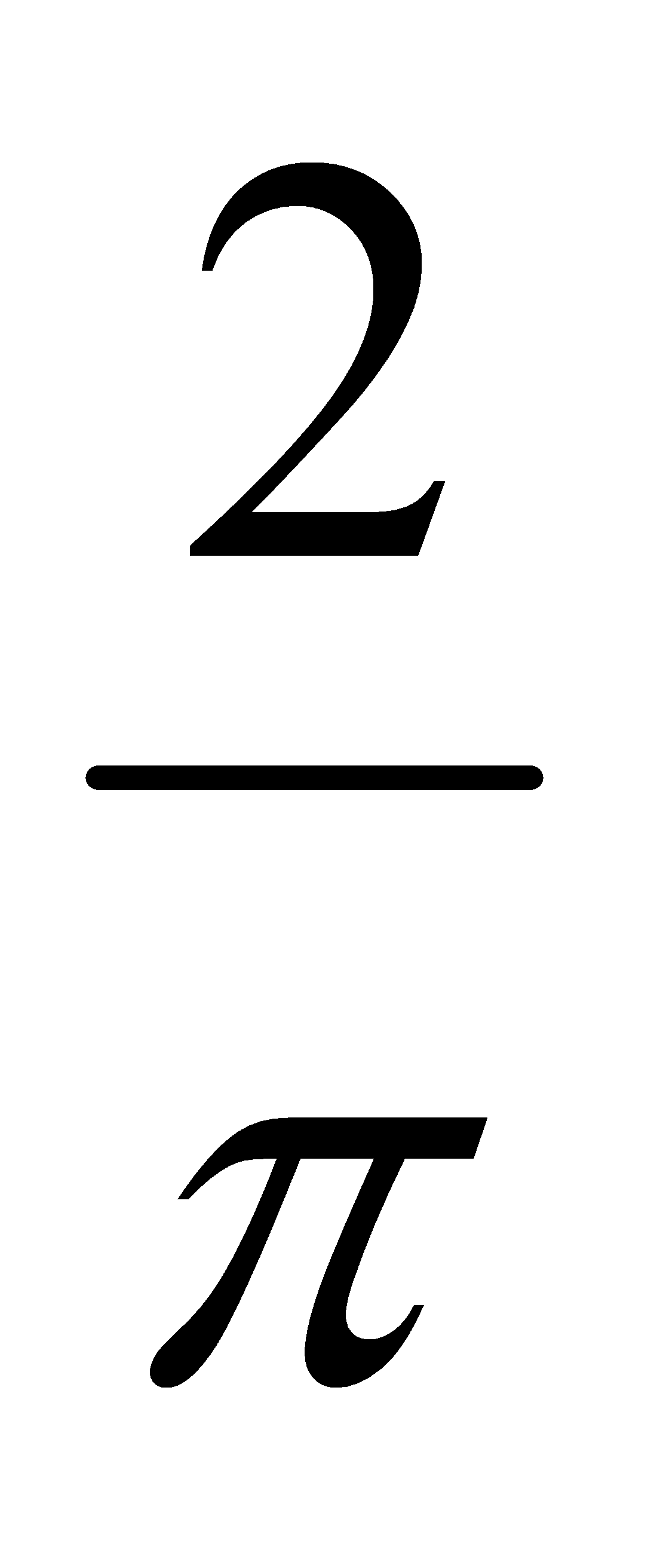
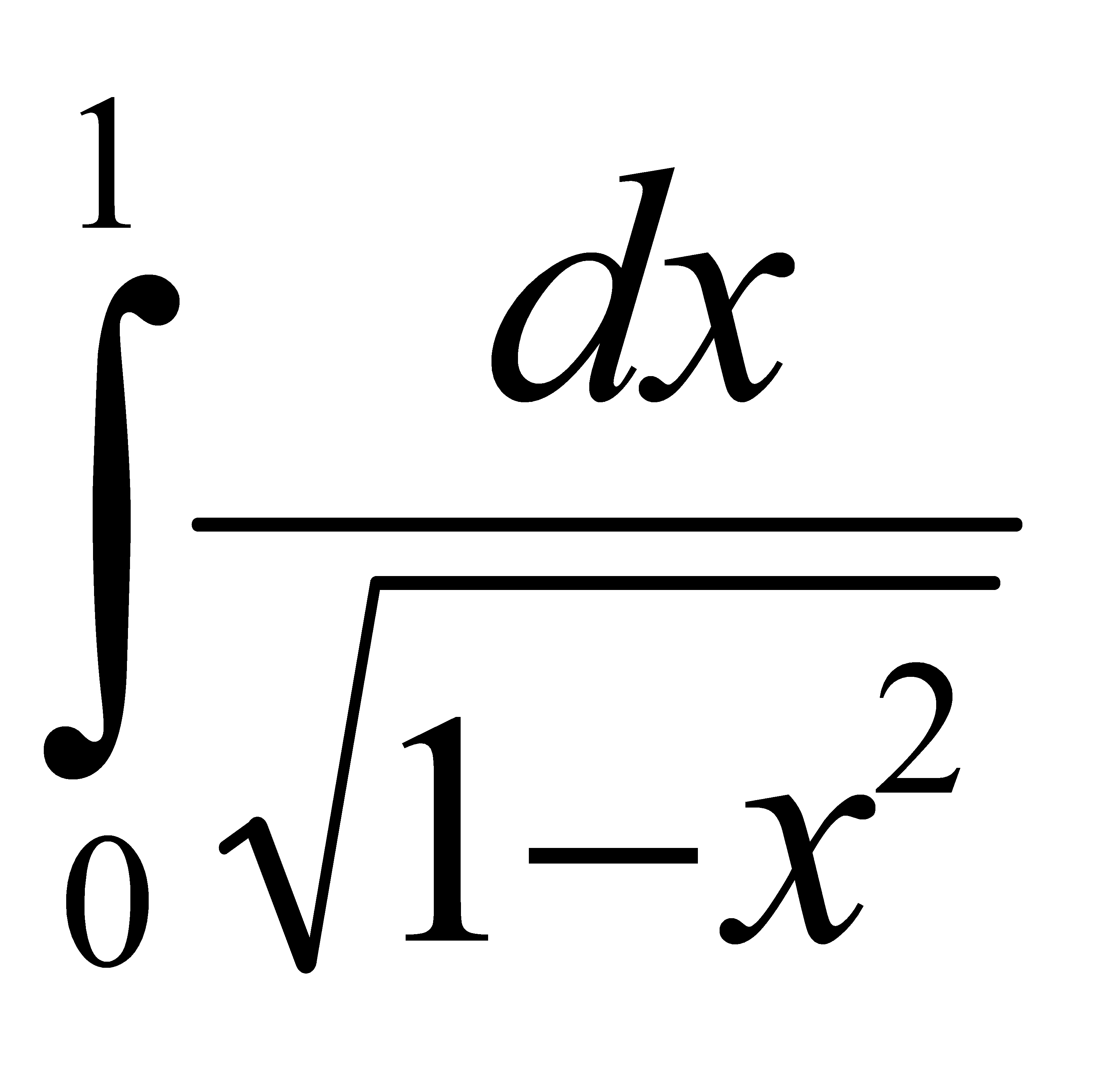 D) 1 G) 2/2 H) 8/8
D) 1 G) 2/2 H) 8/8
Есепте: 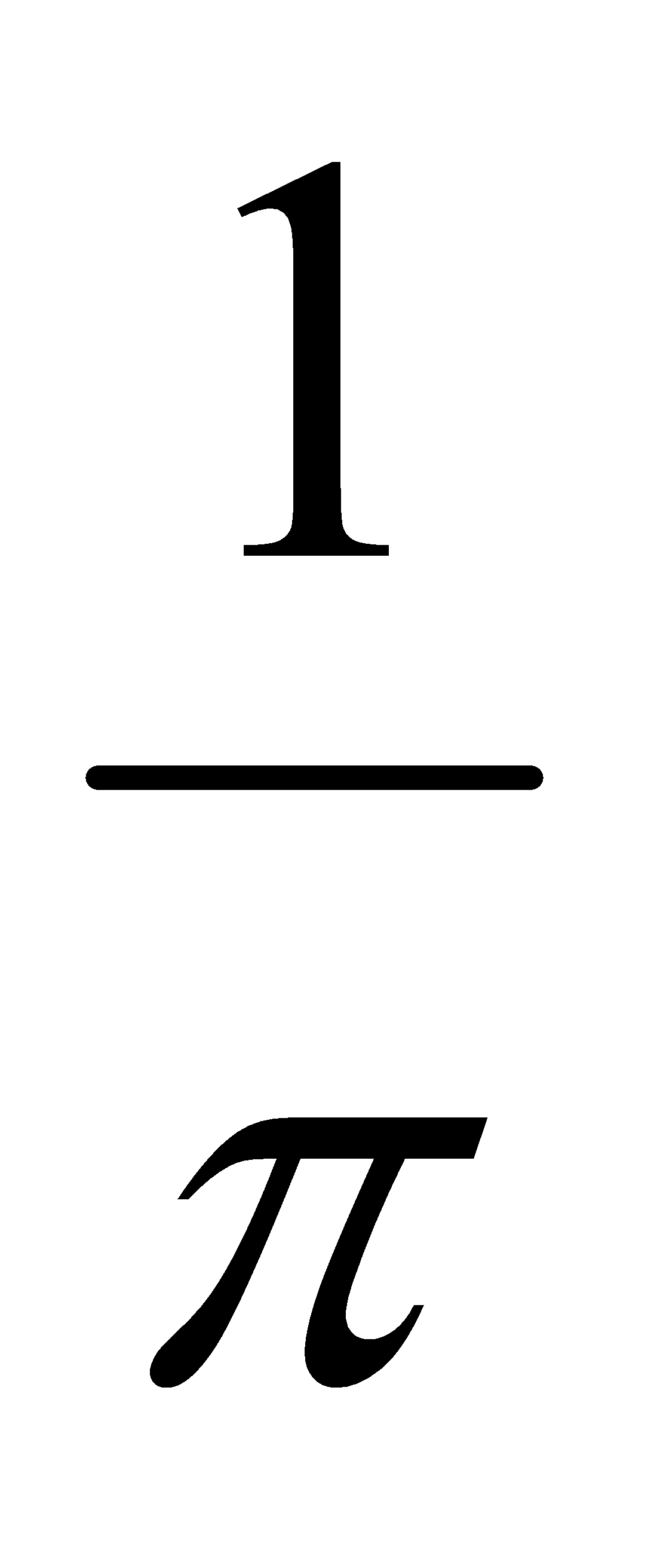
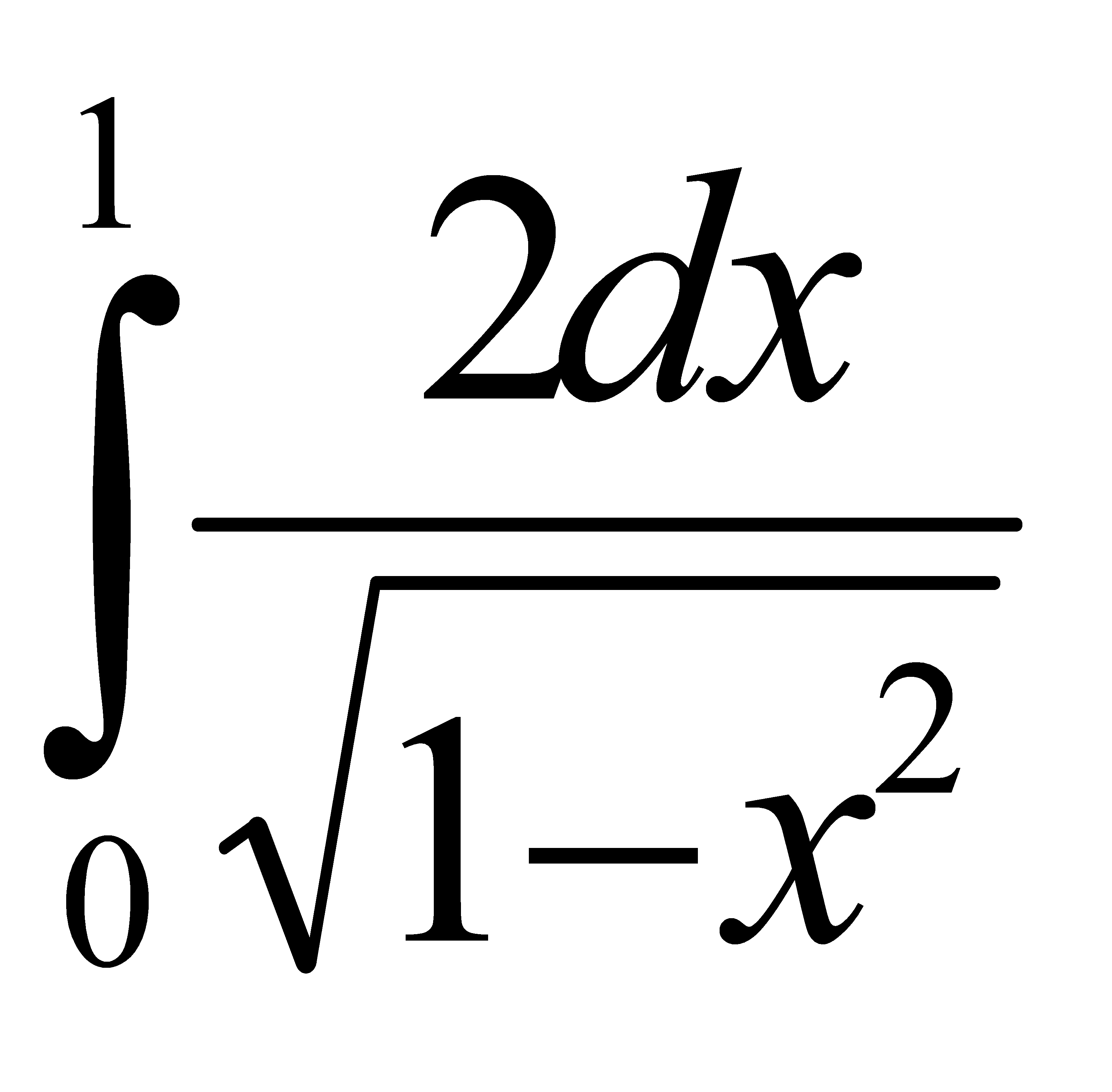 D) 1 G) 2/2 H) 80
D) 1 G) 2/2 H) 80
Есепте: 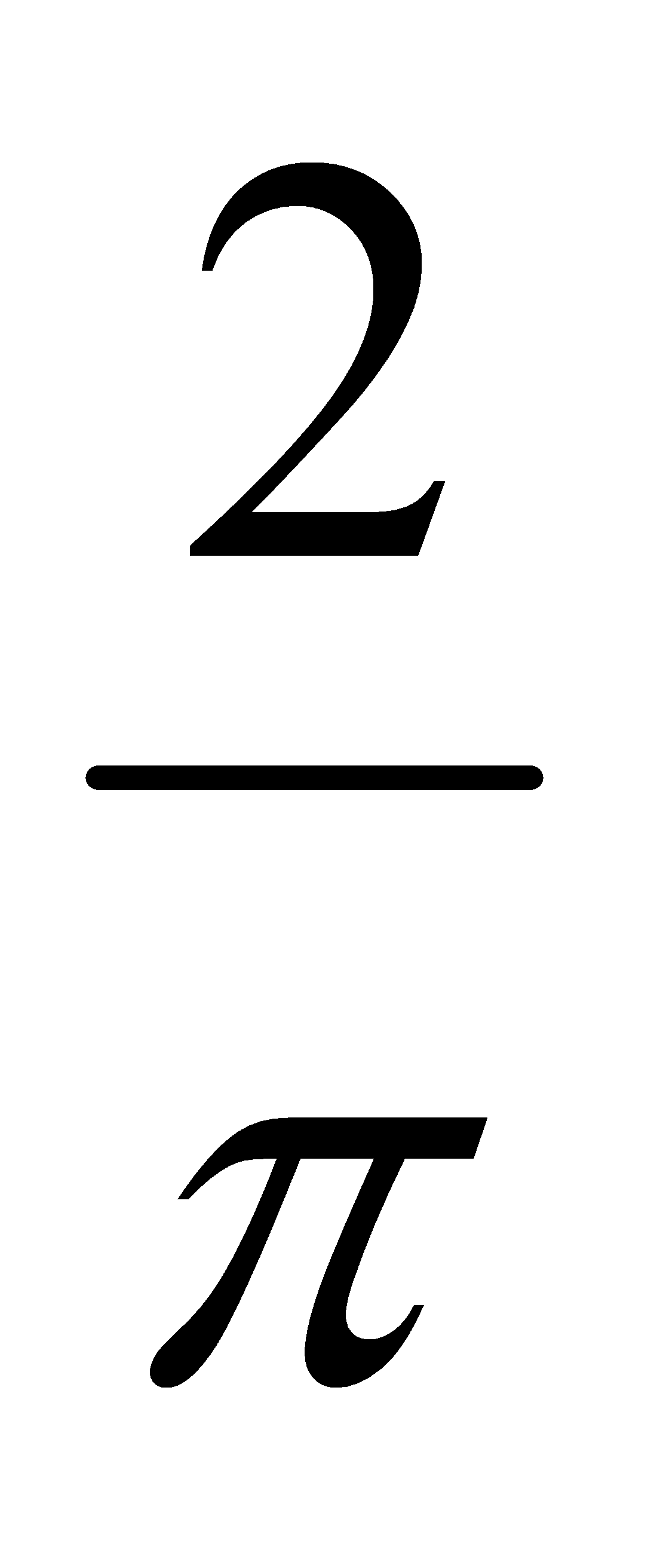
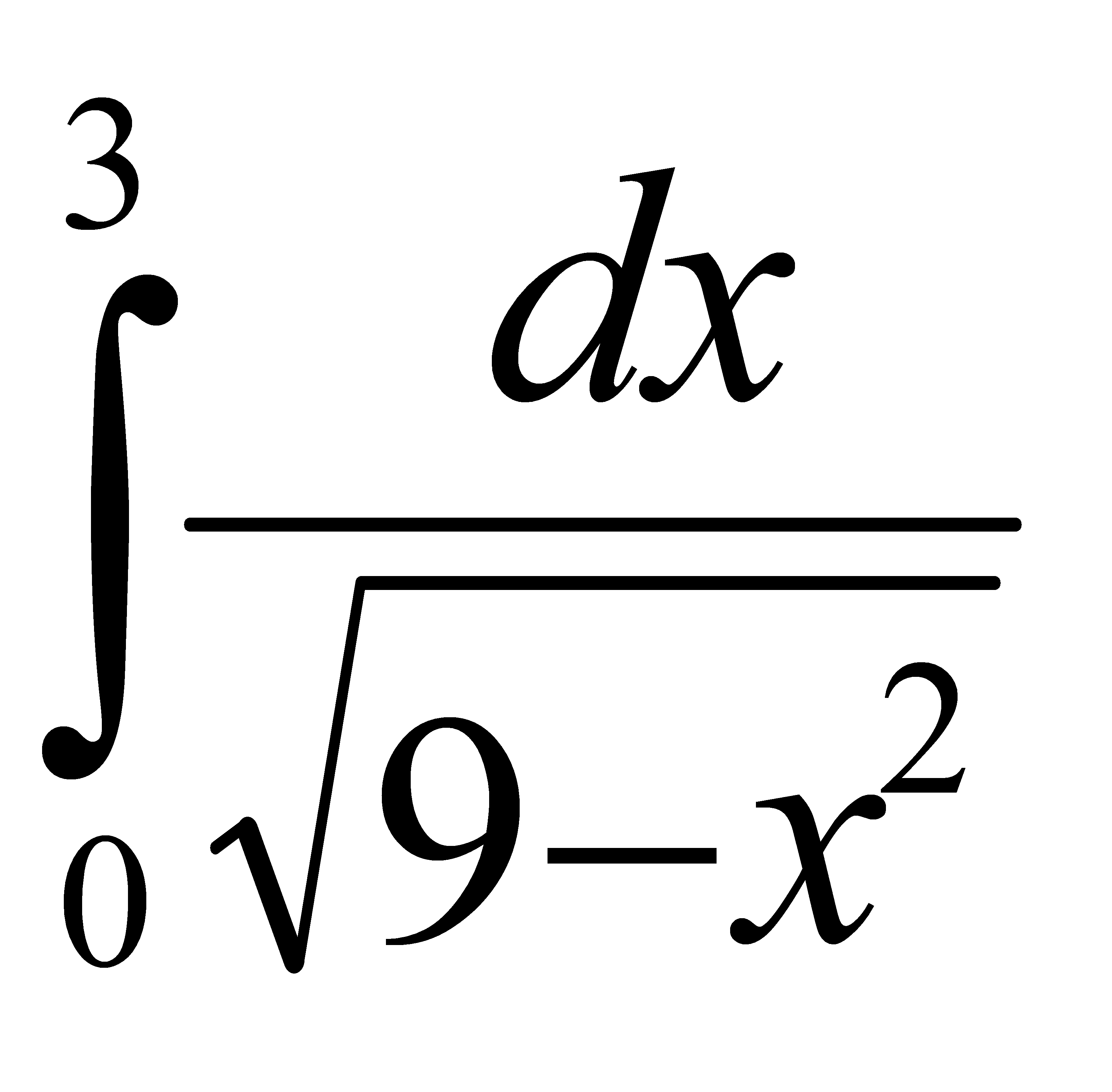 D) 1 G) 2/2H) 8/8
D) 1 G) 2/2H) 8/8
Есепте: 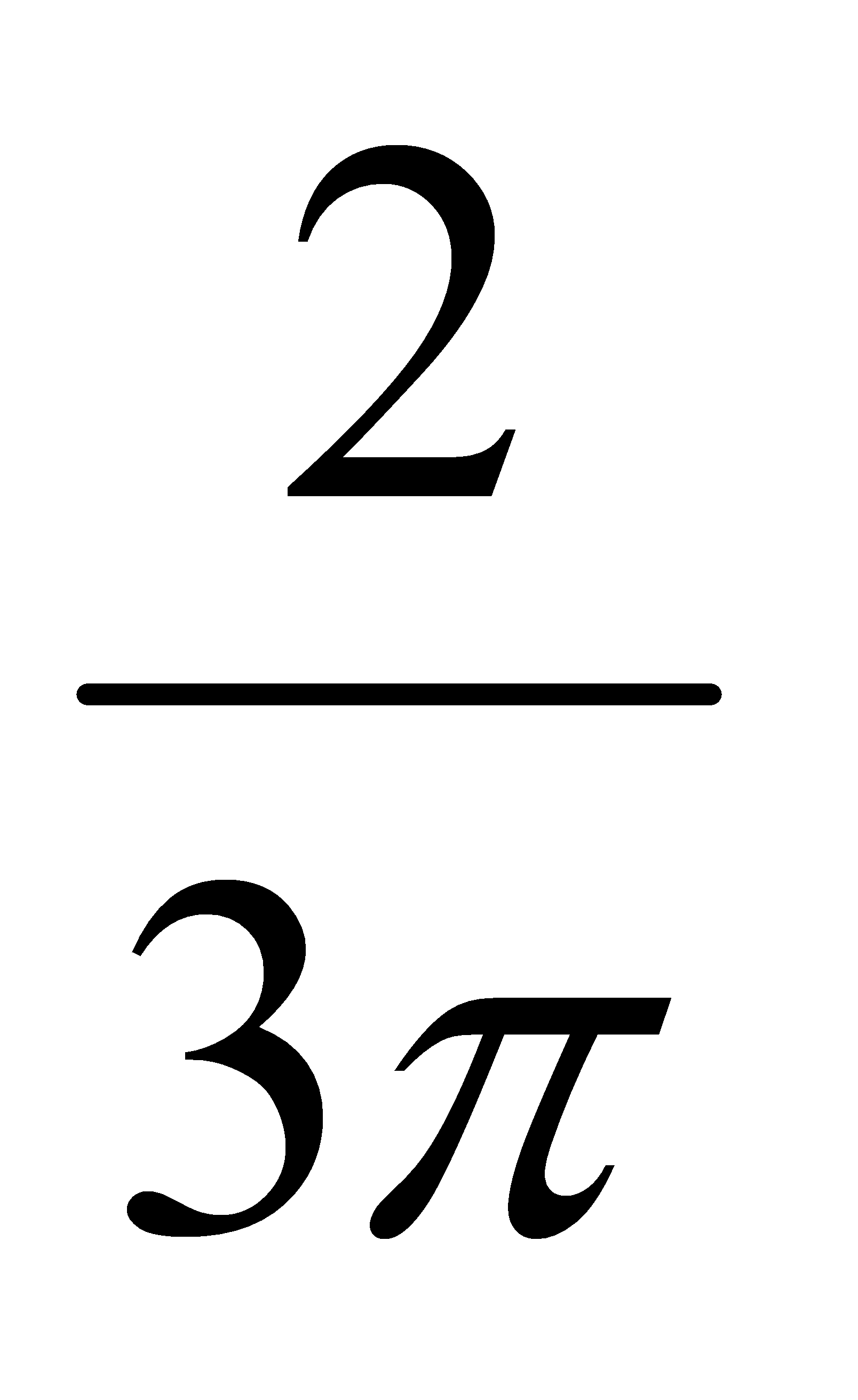
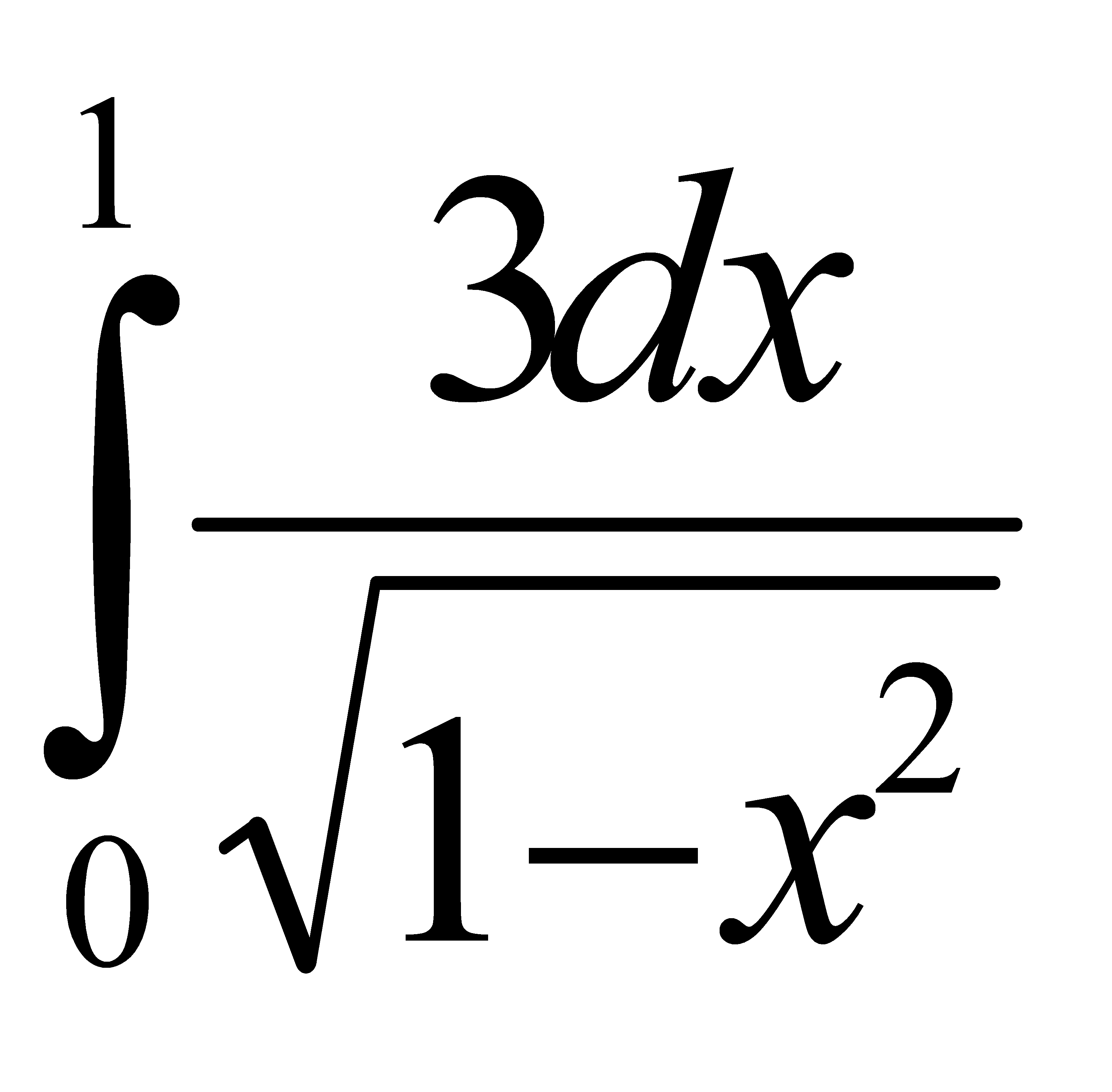 D) 1 G) 20 H) 8/8
D) 1 G) 20 H) 8/8
Есепте: 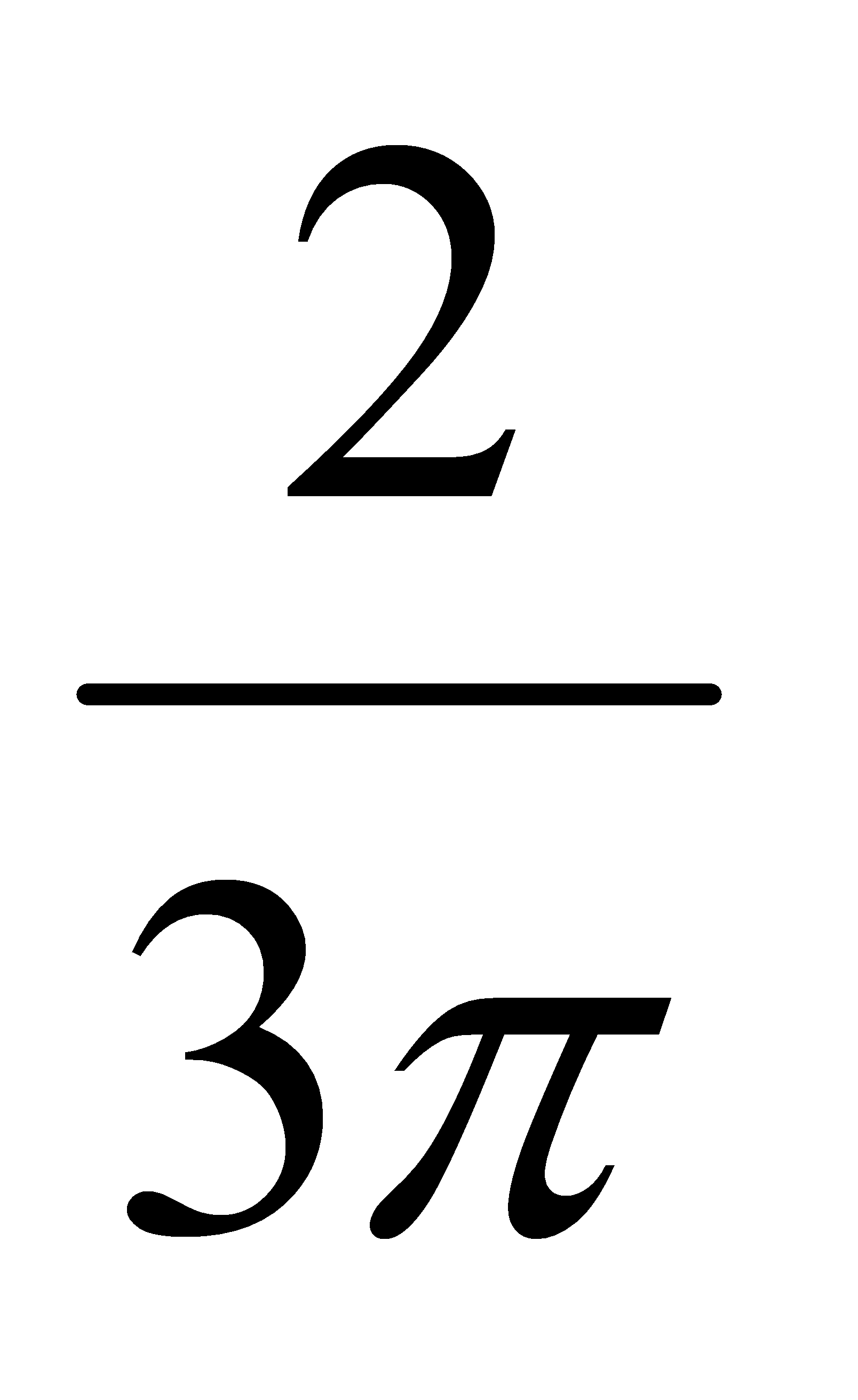
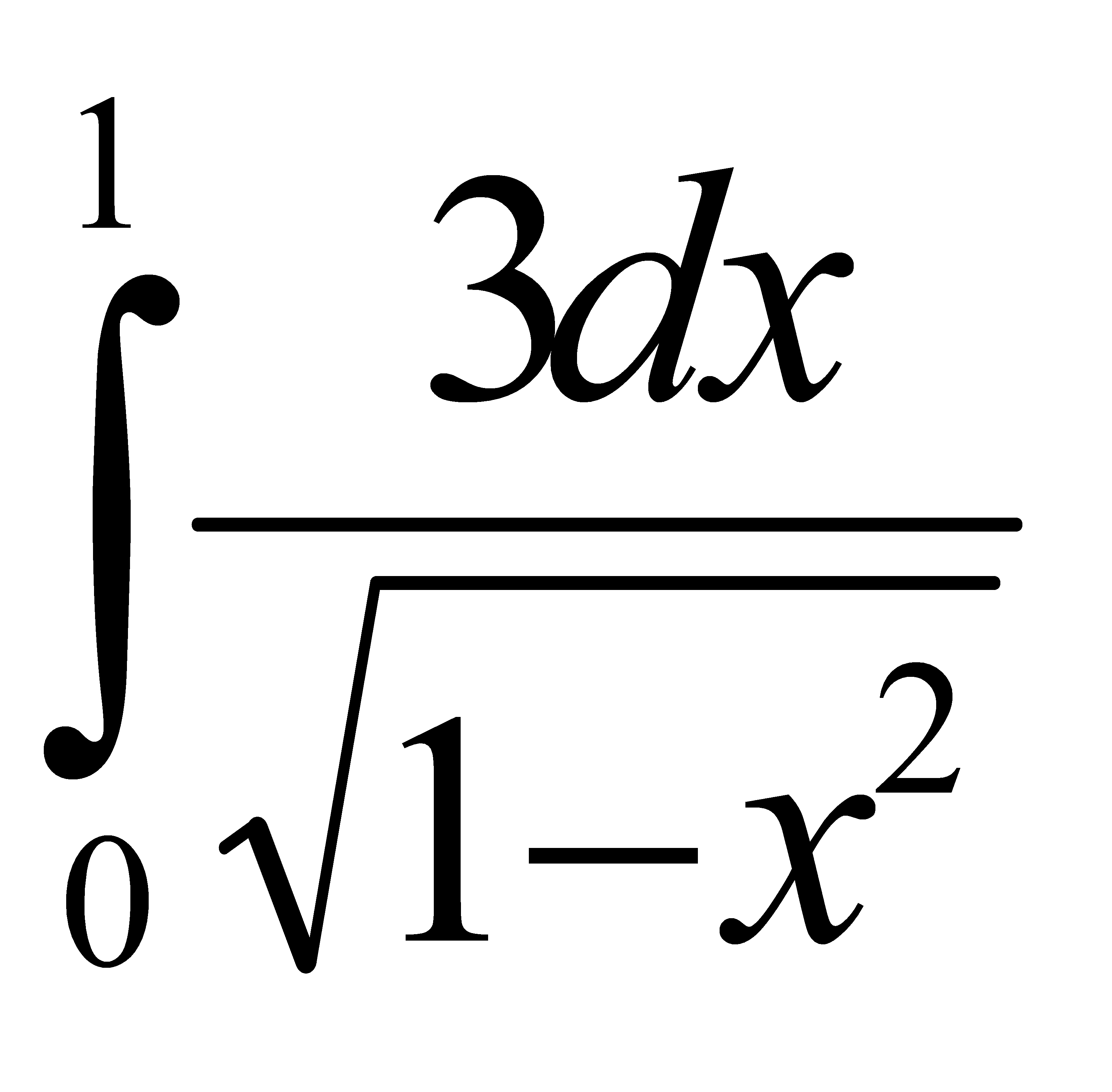 D) 1 G) 20 H) 8/8
D) 1 G) 20 H) 8/8
Есепте: 
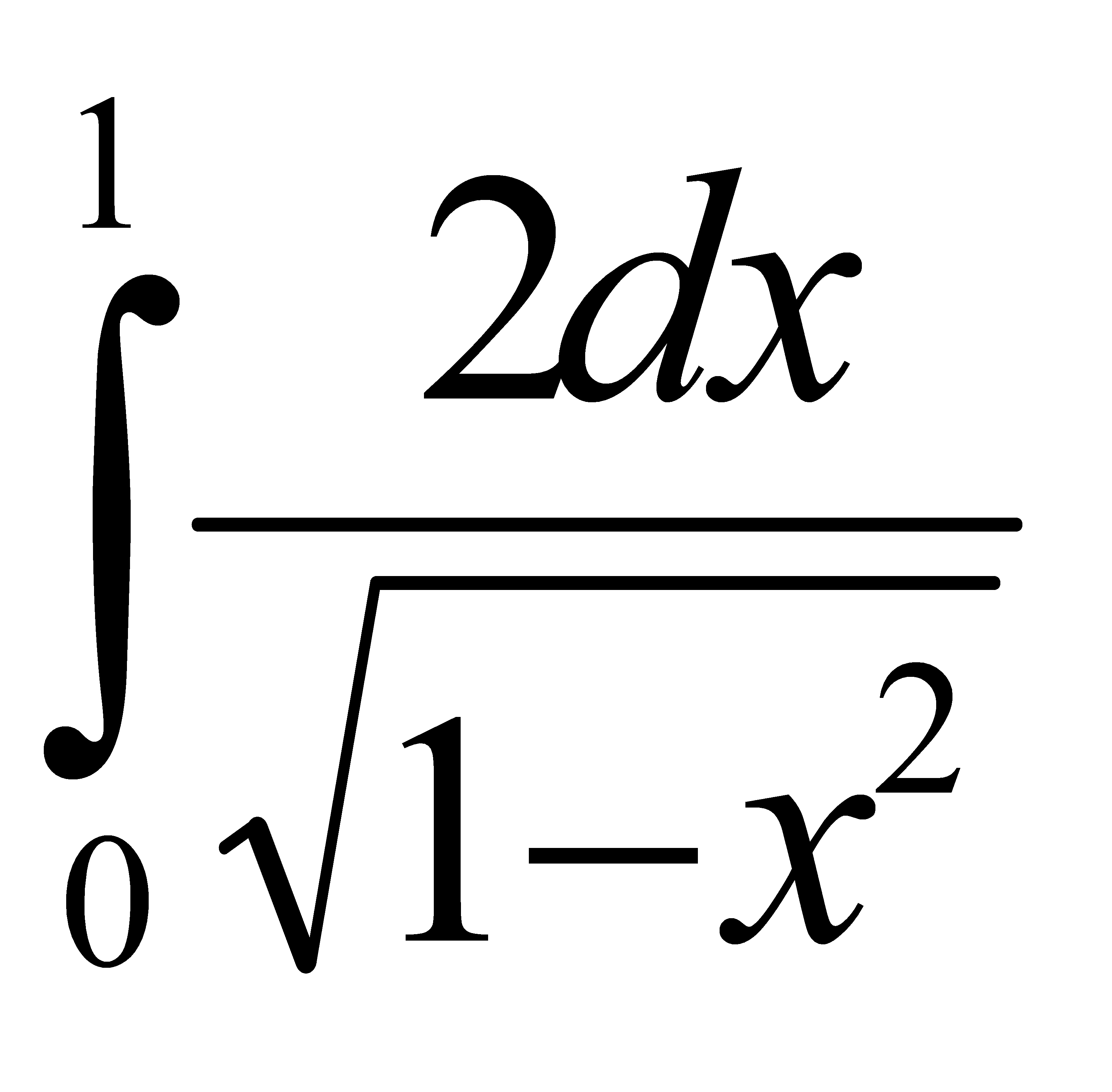 D) 1G) 2/2 H) 80
D) 1G) 2/2 H) 80
Есепте: 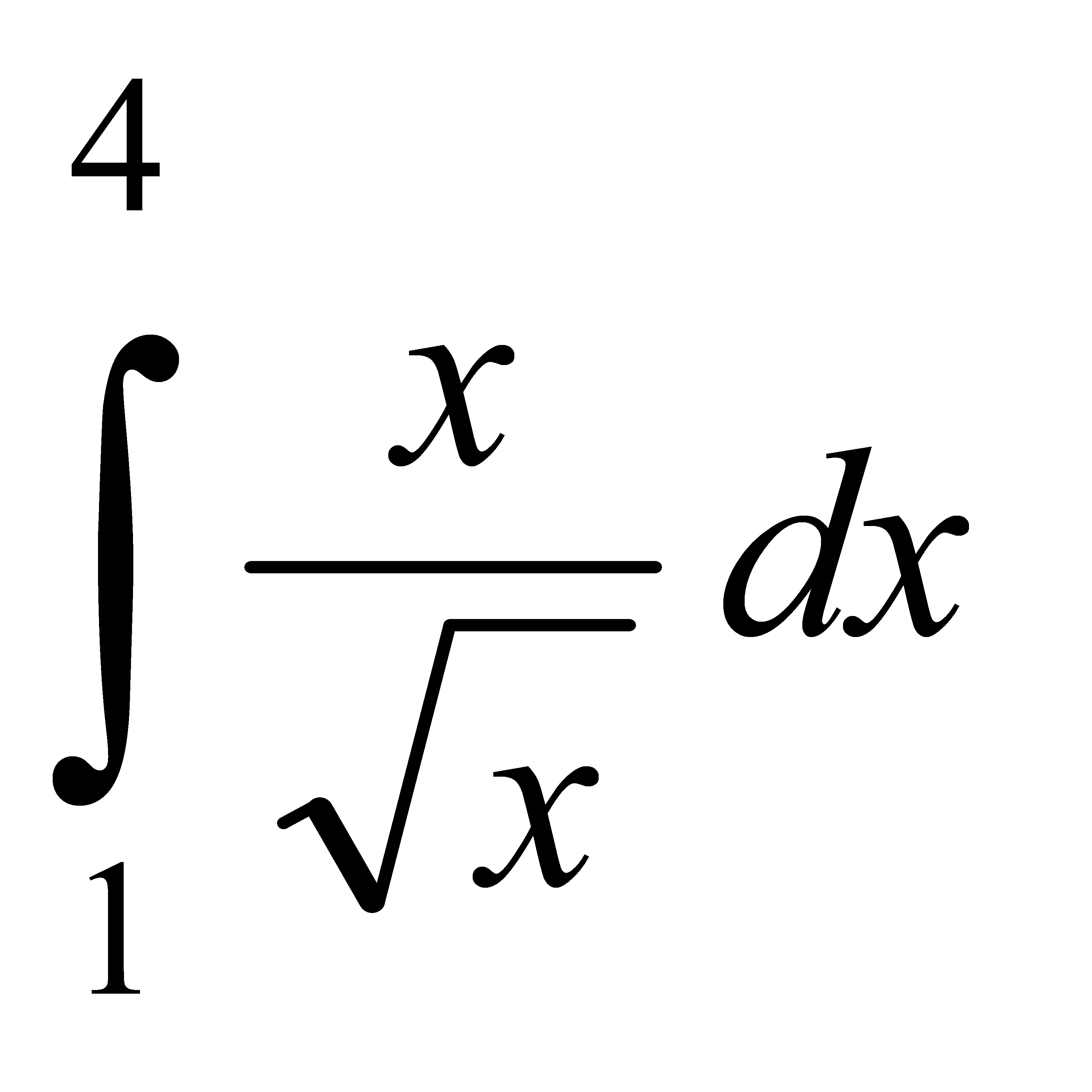 A) 14/3 B) 28/6 E) 42/9
A) 14/3 B) 28/6 E) 42/9
Есепте: 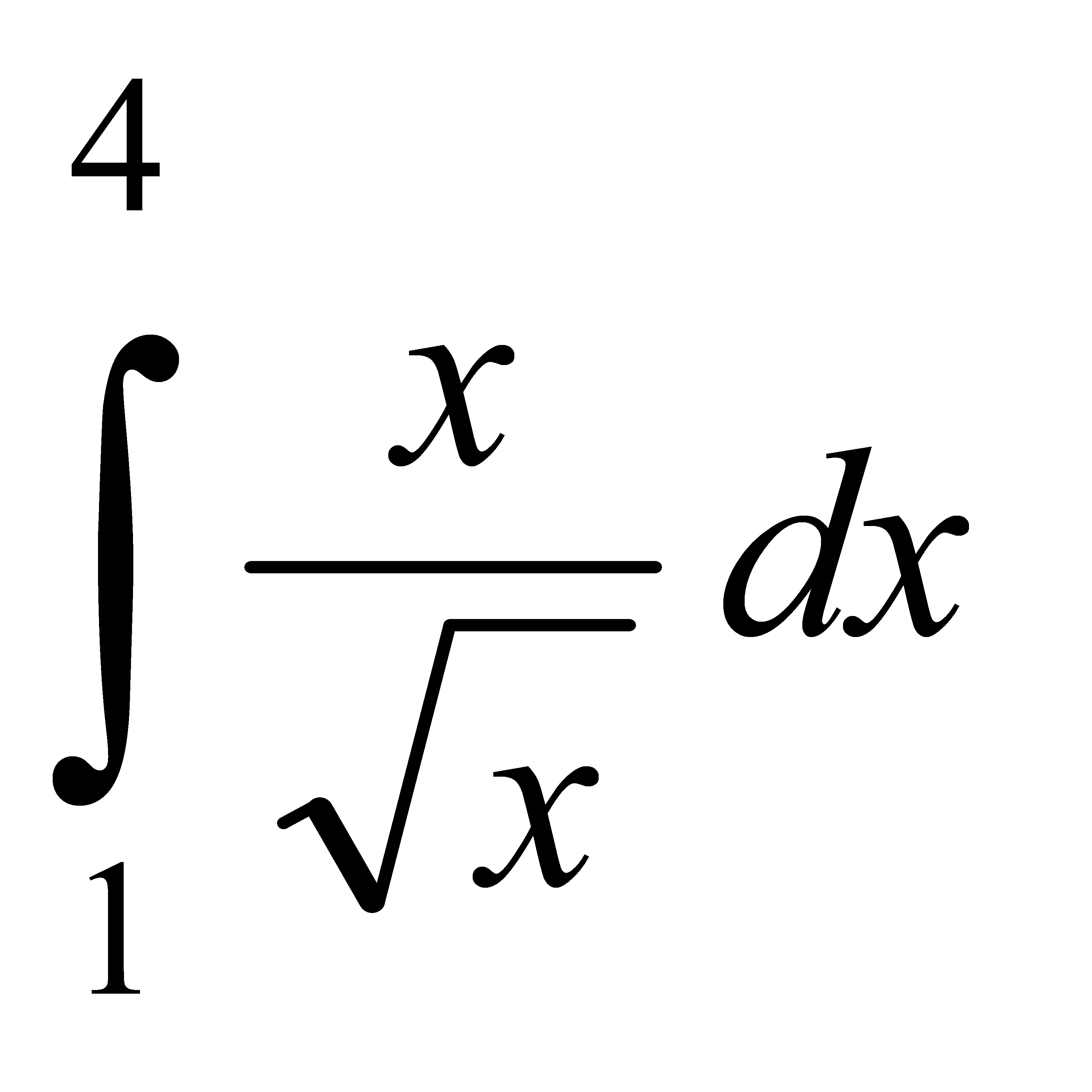 A) 14/3 B) 28/6 E) 42/9
A) 14/3 B) 28/6 E) 42/9
Есепте: 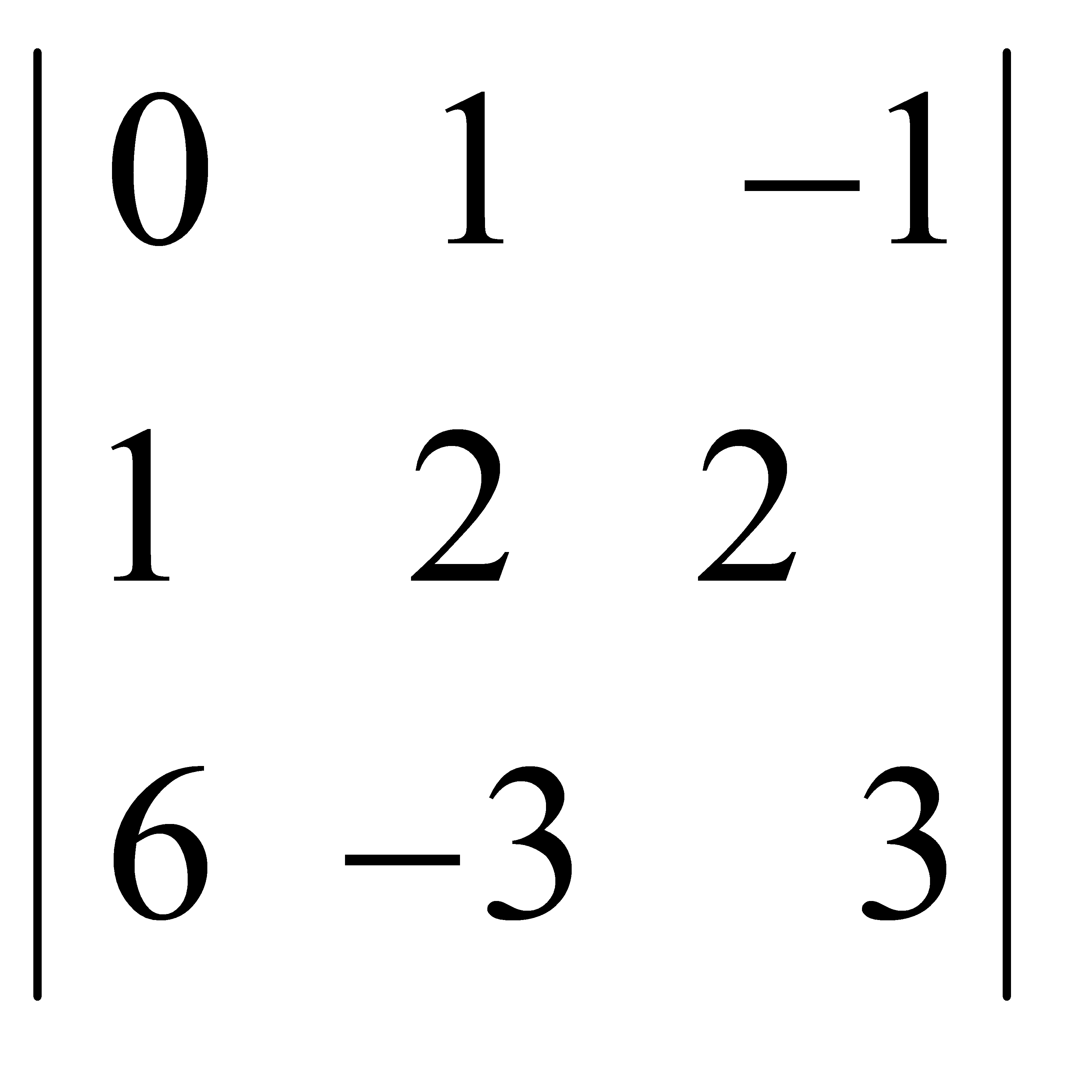 A) 24 C) 48/2 Е) 72/3
A) 24 C) 48/2 Е) 72/3
Есепте:  A) –28 B)-56/2 C)-84/3
A) –28 B)-56/2 C)-84/3
Есепте: 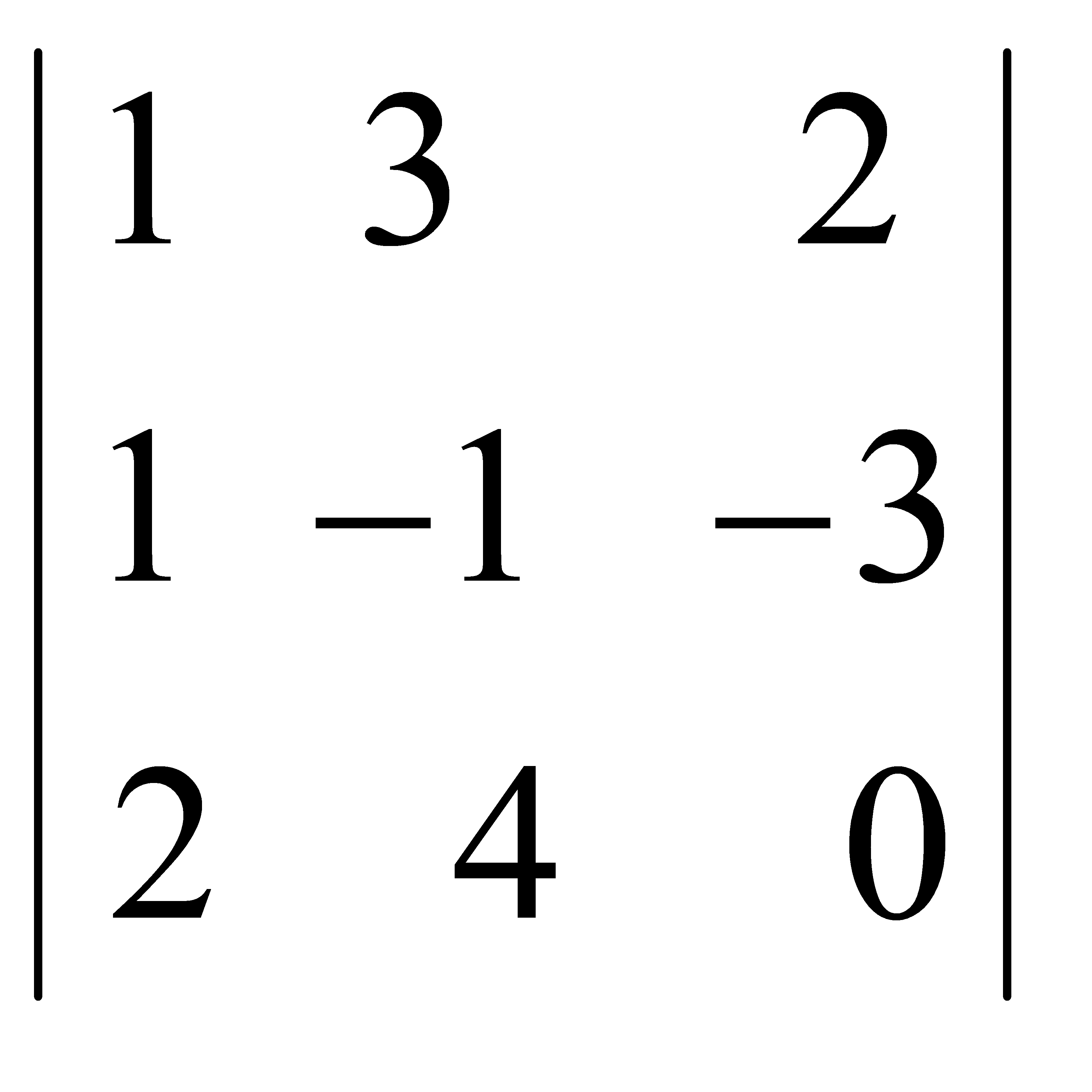 A) 6 C) 12/2 E) 18/3
A) 6 C) 12/2 E) 18/3
Есепте: 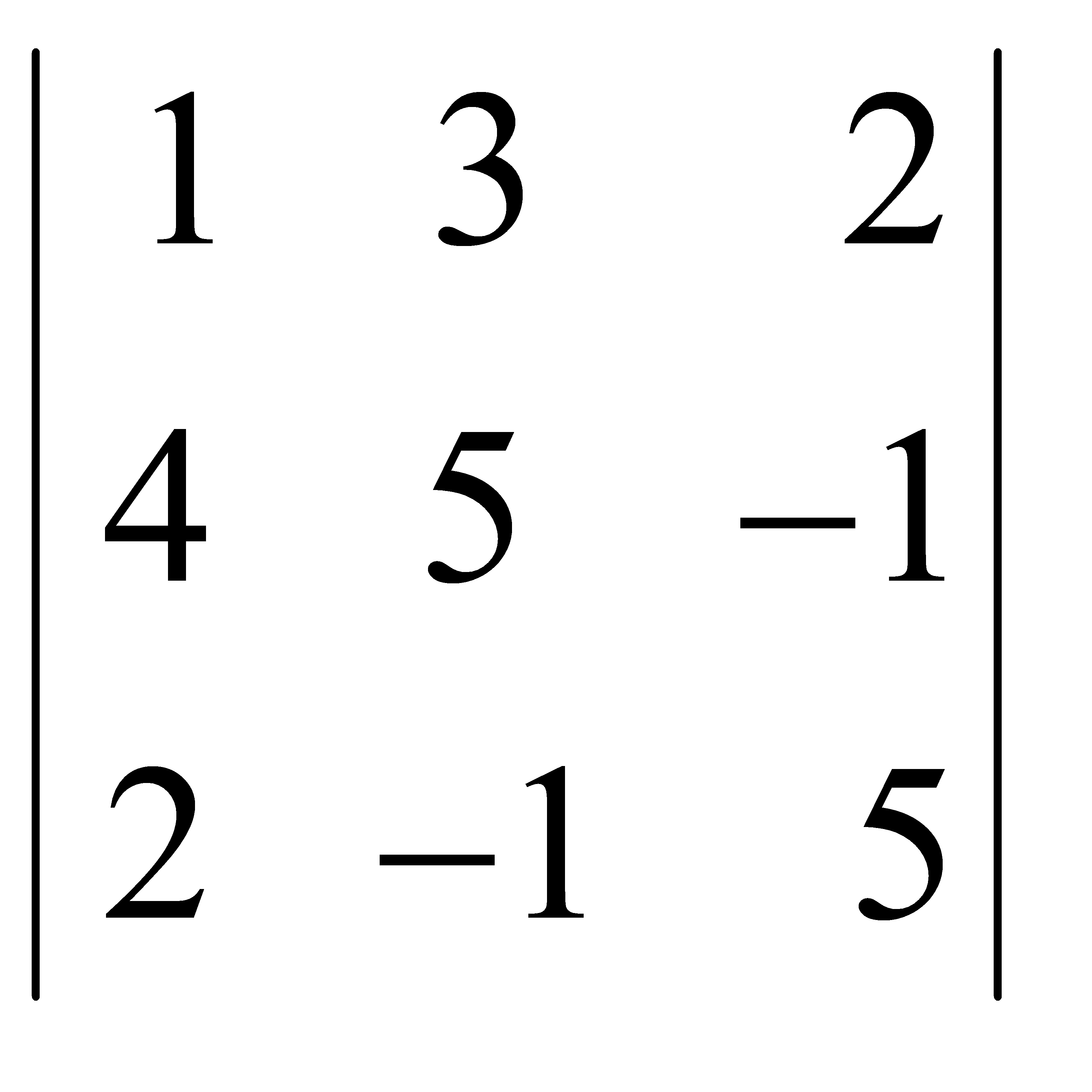 A) -70 C)-140/2 G)-210/3
A) -70 C)-140/2 G)-210/3
Есепте: 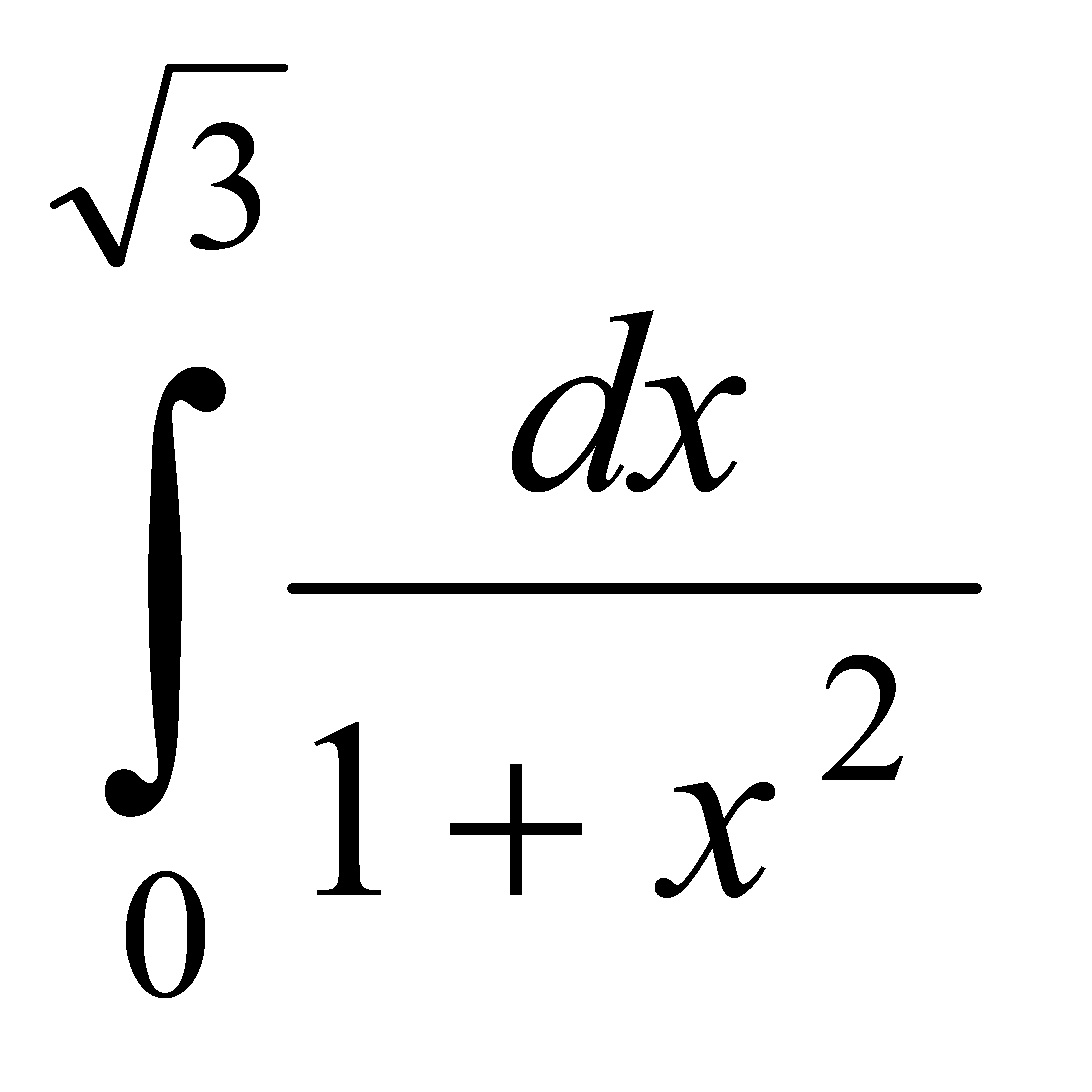 A) p/3 C) 2 p/6 H) 3p/9
A) p/3 C) 2 p/6 H) 3p/9
Есепте: 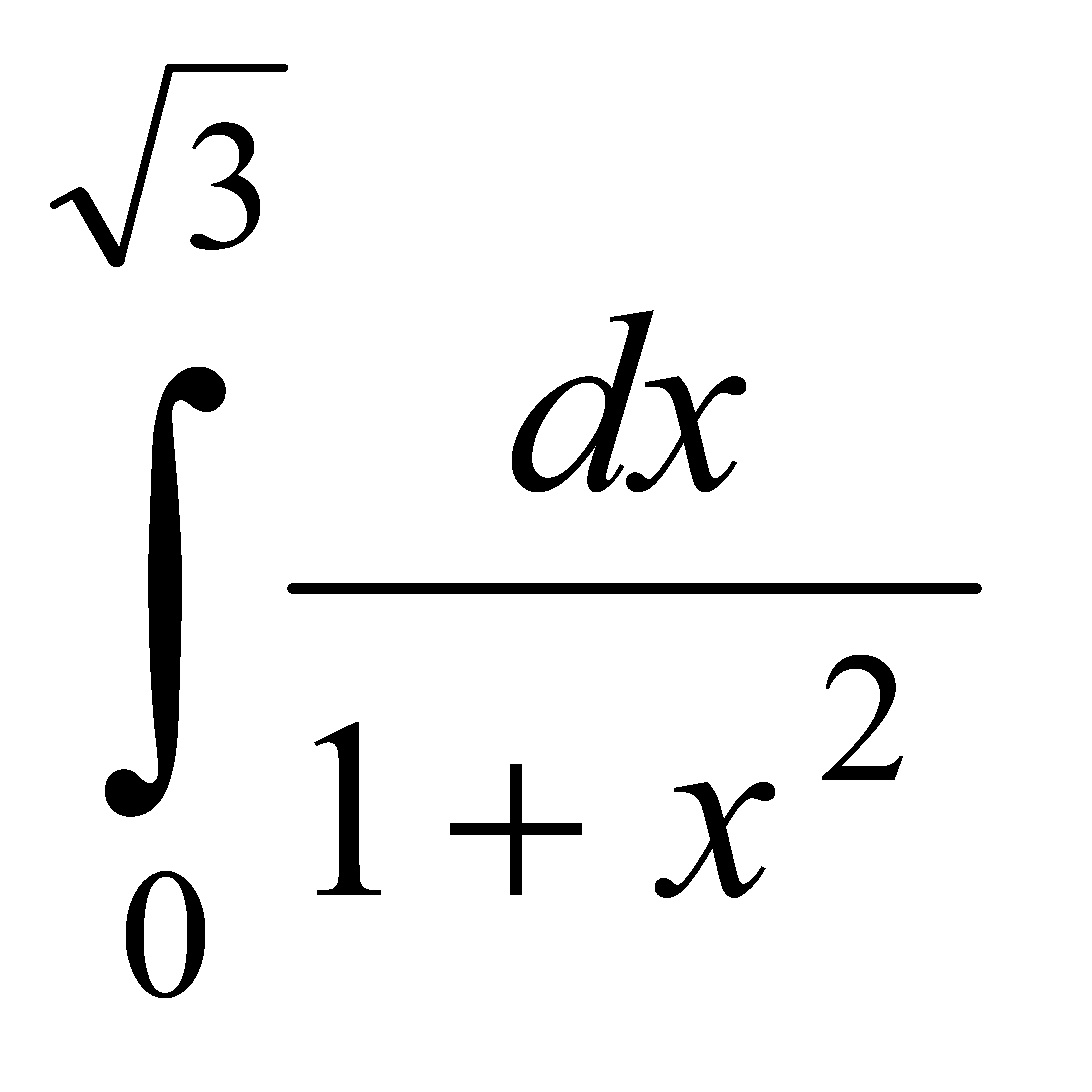 A) p/3 C) 2 p/6 H) 3p/9
A) p/3 C) 2 p/6 H) 3p/9
Есепте: 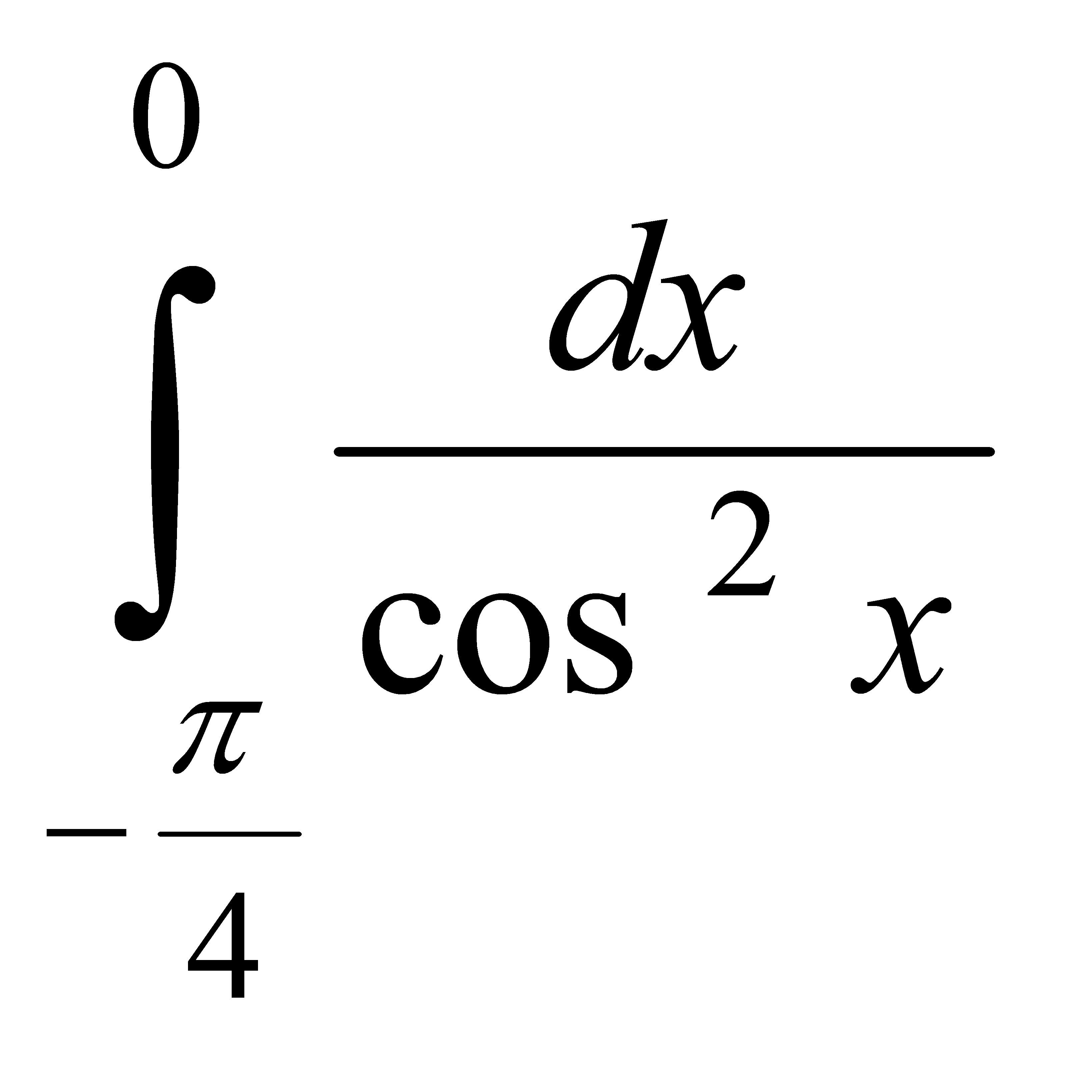 D) 1 G) 2/2 H) 8/8
D) 1 G) 2/2 H) 8/8
Есепте: 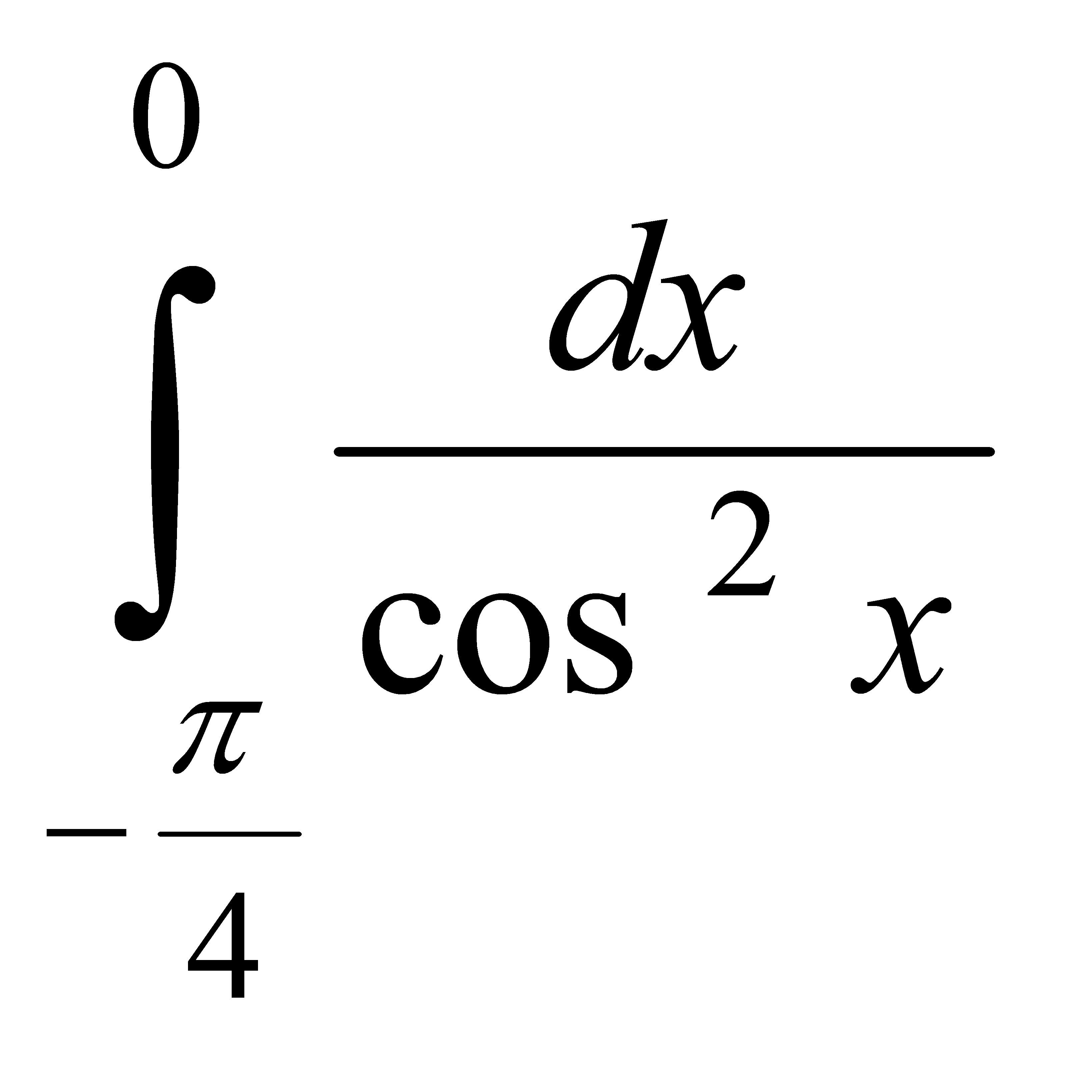 D) 1 G) 2/2 H) 8/8
D) 1 G) 2/2 H) 8/8
Есептеңіз: 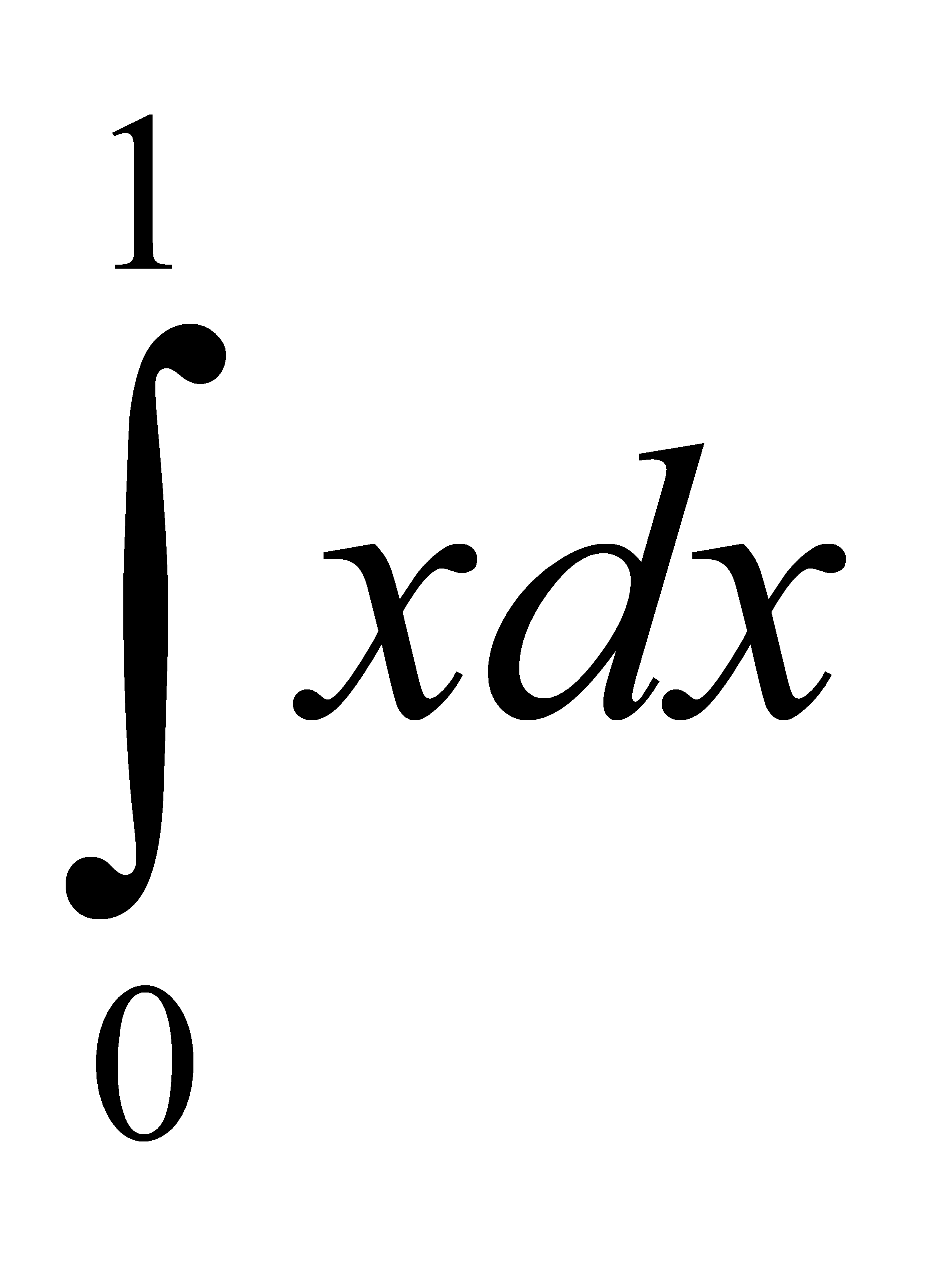 A) 0,5 E) ½ H) 2/4
A) 0,5 E) ½ H) 2/4
Есептеңіз: 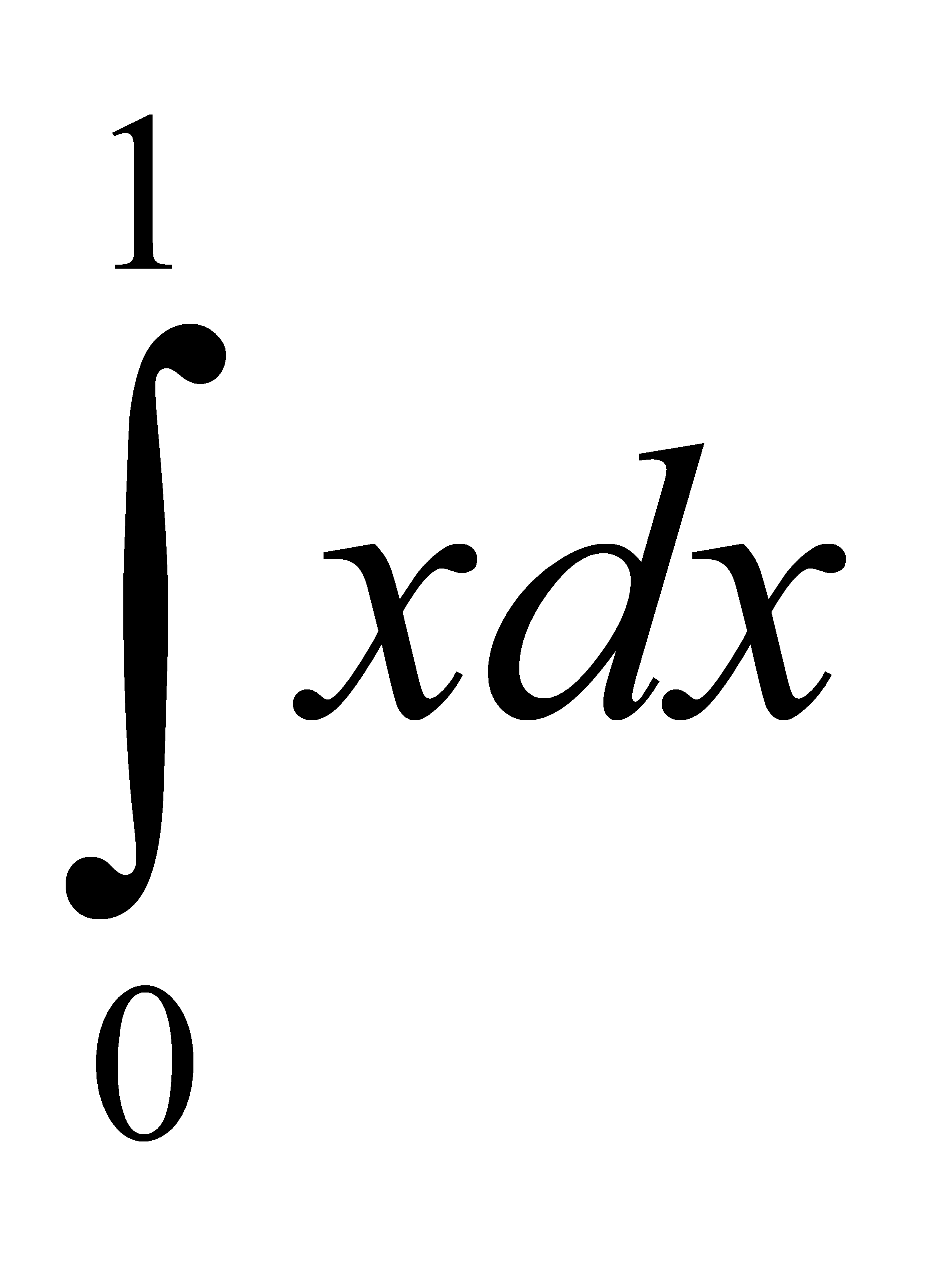 A) 0,5 E) ½ H) 2/4
A) 0,5 E) ½ H) 2/4
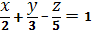 жазықтығы:A)
жазықтығы:A) 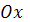 өсінен 2-ге тең кесінді қияды B)
өсінен 2-ге тең кесінді қияды B) 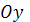 өсінен 3-ке тең кесінді қияды F)
өсінен 3-ке тең кесінді қияды F) 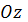 өсін -5-ке тең нүктеде қияды
өсін -5-ке тең нүктеде қияды
 жазықтығы:B)
жазықтығы:B) 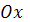 өсінен 2-ге тең кесінді қияды E) координаталық өстерден 2-ге тең кесінділер қияды H) координаталық өстерден бірдей кесінді қияды
өсінен 2-ге тең кесінді қияды E) координаталық өстерден 2-ге тең кесінділер қияды H) координаталық өстерден бірдей кесінді қияды
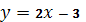 және
және 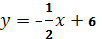 түзулері:A) әртүрлі бұрыштық коэффициентке ие G) перпендикуляр H) 90° бұрыш жасайды
түзулері:A) әртүрлі бұрыштық коэффициентке ие G) перпендикуляр H) 90° бұрыш жасайды
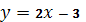 және
және 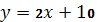 түзулеріB) бірдей бұрыштық коэффициентке ие C) 0° бұрыш жасайды F) параллель
түзулеріB) бірдей бұрыштық коэффициентке ие C) 0° бұрыш жасайды F) параллель
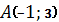 және
және 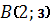 нүктелері арқылы өтетін түзудің теңдеуі: A)
нүктелері арқылы өтетін түзудің теңдеуі: A) 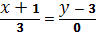 C)
C) 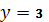 E)
E) 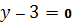
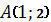 және
және  нүктелері арқылы өтетін түзудің теңдеуі: B)
нүктелері арқылы өтетін түзудің теңдеуі: B) 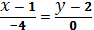 D)
D) 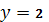 G)
G) 
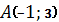 және
және 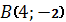 нүктелері арқылы өтетін түзудің теңдеуі:A)
нүктелері арқылы өтетін түзудің теңдеуі:A) 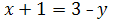 C)
C) 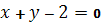 H)
H) 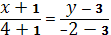
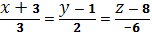 және
және 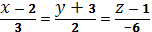 түзулері:B) параллель E)
түзулері:B) параллель E) 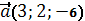 бағыттаушы векторына ие G) 0° бұрыш жасайды
бағыттаушы векторына ие G) 0° бұрыш жасайды
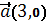 және
және 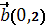 векторлардан құрылған паралелограммның ауданы:A)6 E)бүтін сан G)оң сан
векторлардан құрылған паралелограммның ауданы:A)6 E)бүтін сан G)оң сан
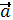 және
және 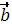 векторларының векторлық көбейтіндісі деп төмендегі шарттарды қанағаттандыратын
векторларының векторлық көбейтіндісі деп төмендегі шарттарды қанағаттандыратын 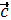 векторын атайды: A)
векторын атайды: A) 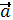 векторына да,
векторына да, 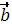 векторына да перпендикуляр C)осы векторлармен реттелген оң үштік құрайды E)ұзындығы
векторына да перпендикуляр C)осы векторлармен реттелген оң үштік құрайды E)ұзындығы 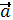 және
және 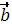 векторларынан құрылған параллелограммның ауданына тең
векторларынан құрылған параллелограммның ауданына тең
Жинақтылыққа Даламбер белгісімен зерттелетін қатардың жалпы мүшесі:A) 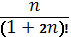 C)
C) 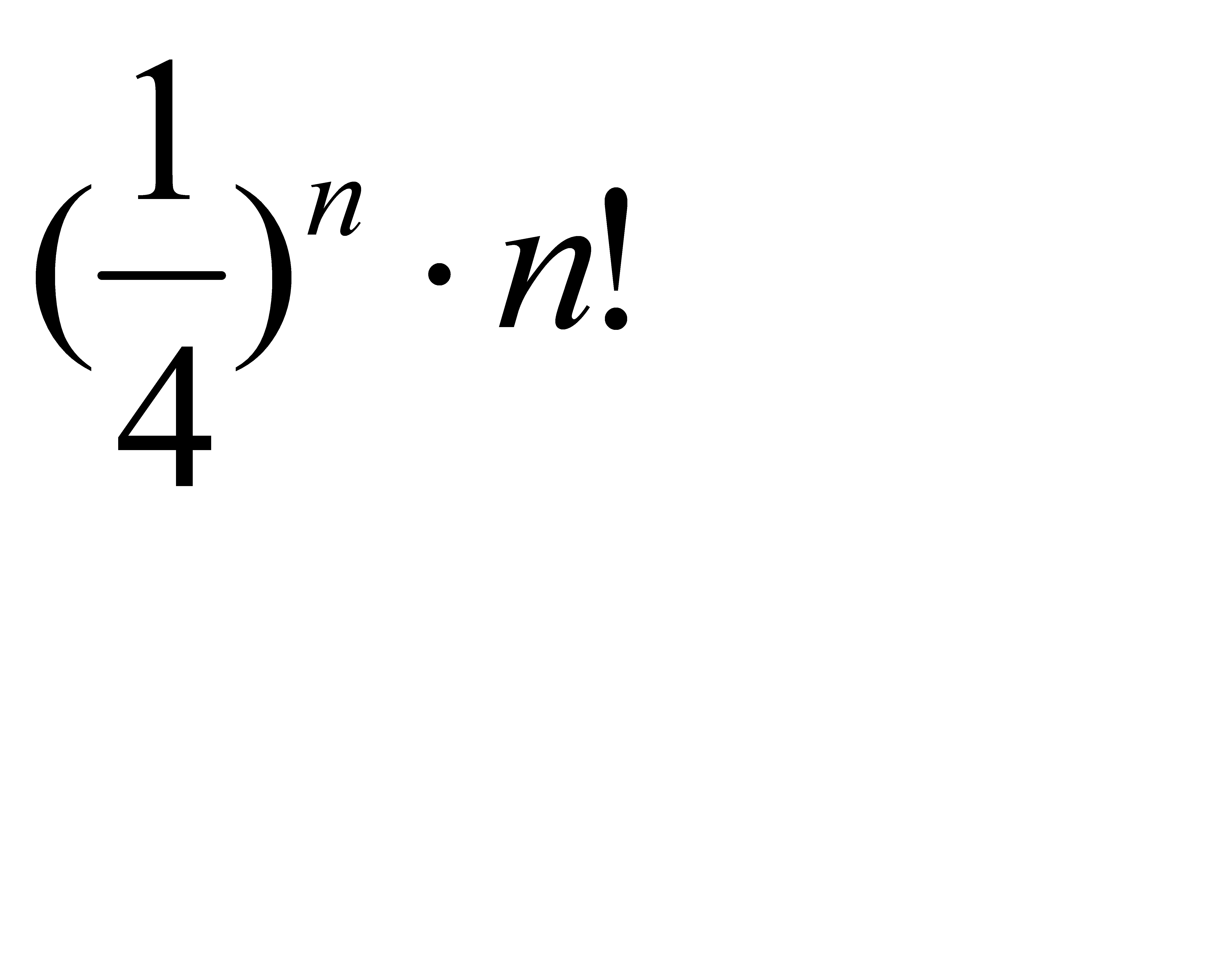 E)
E) 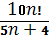
Жинақтылыққа Даламбер белгісімен зерттелетін қатардың жалпы мүшесі:C) 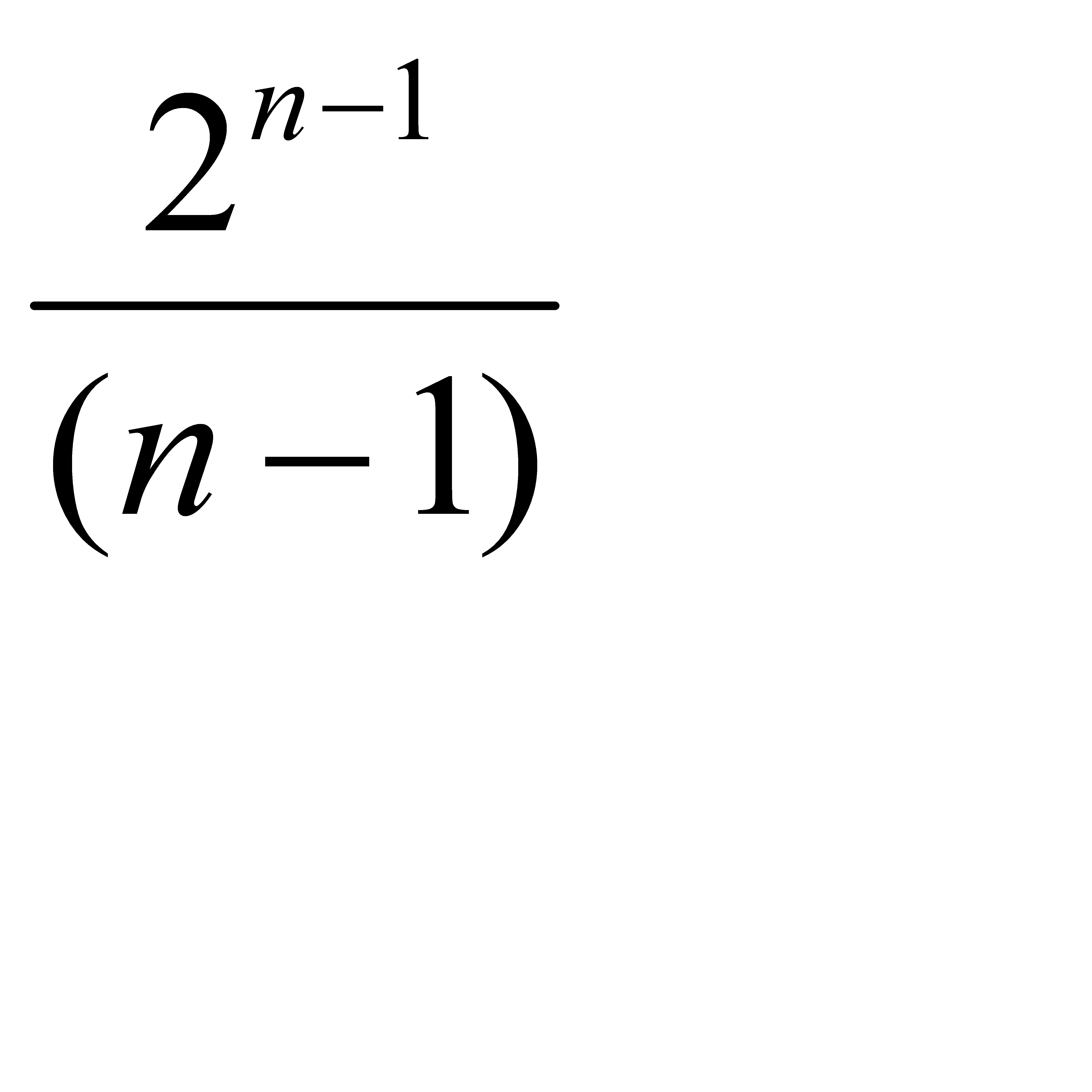 D)
D) 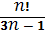 E)
E) 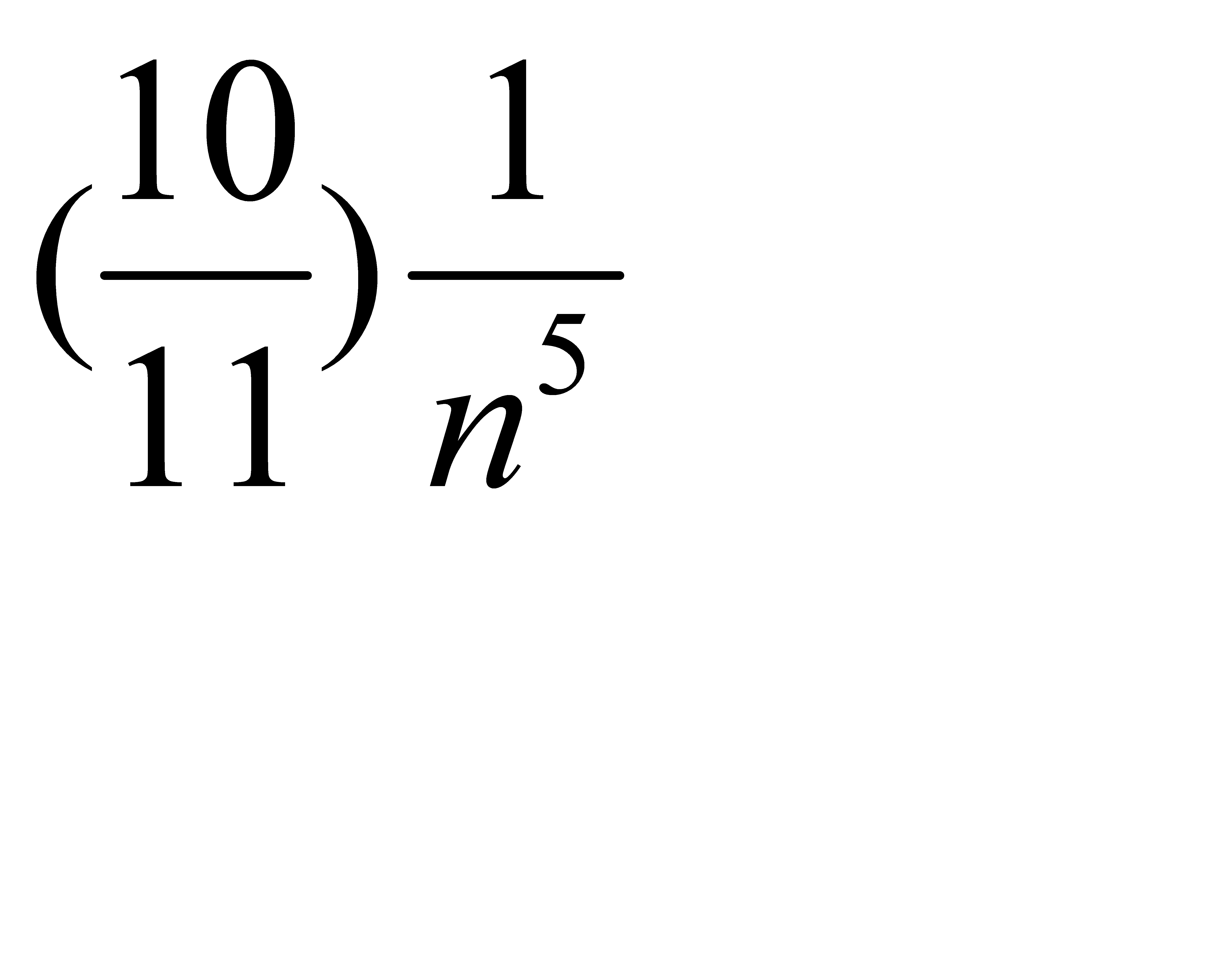
Жинақтылыққа Кошидің радикалдық белгісімен зерттелетін қатардың жалпы мүшесі: A) 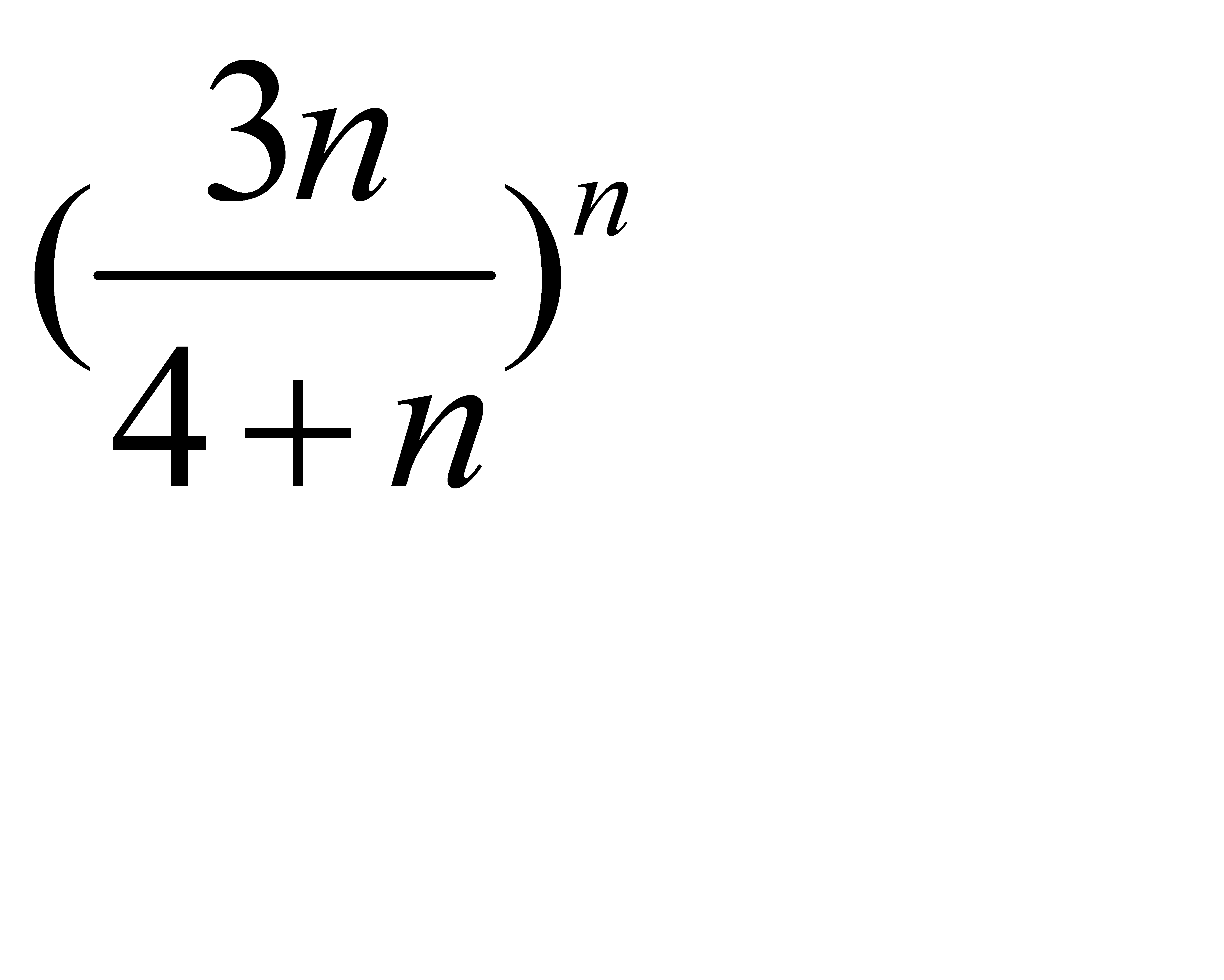 C) D)
C) D) 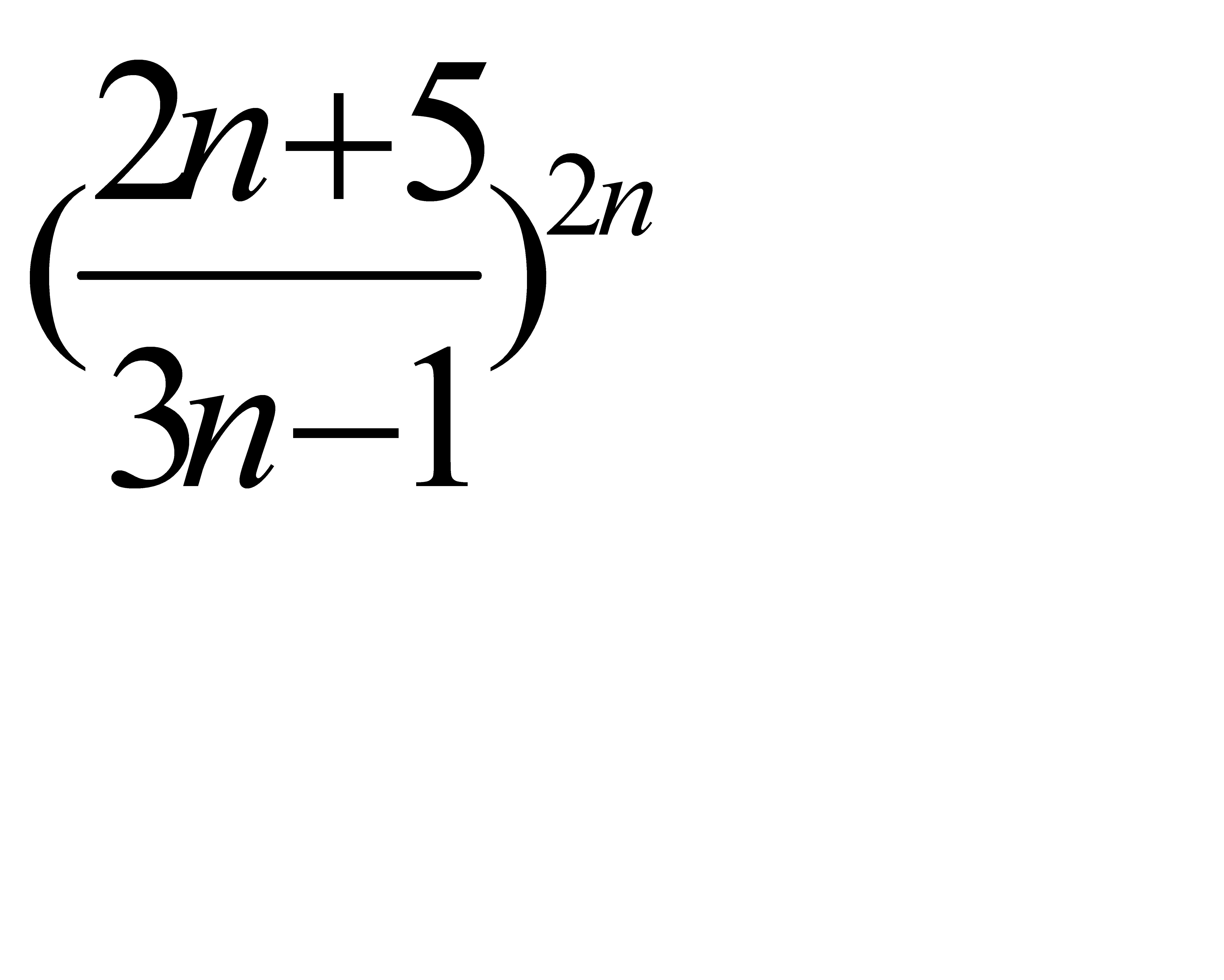
Жинақтылыққа Кошидің радикалдық белгісімен зерттелетін қатардың жалпы мүшесі: A) 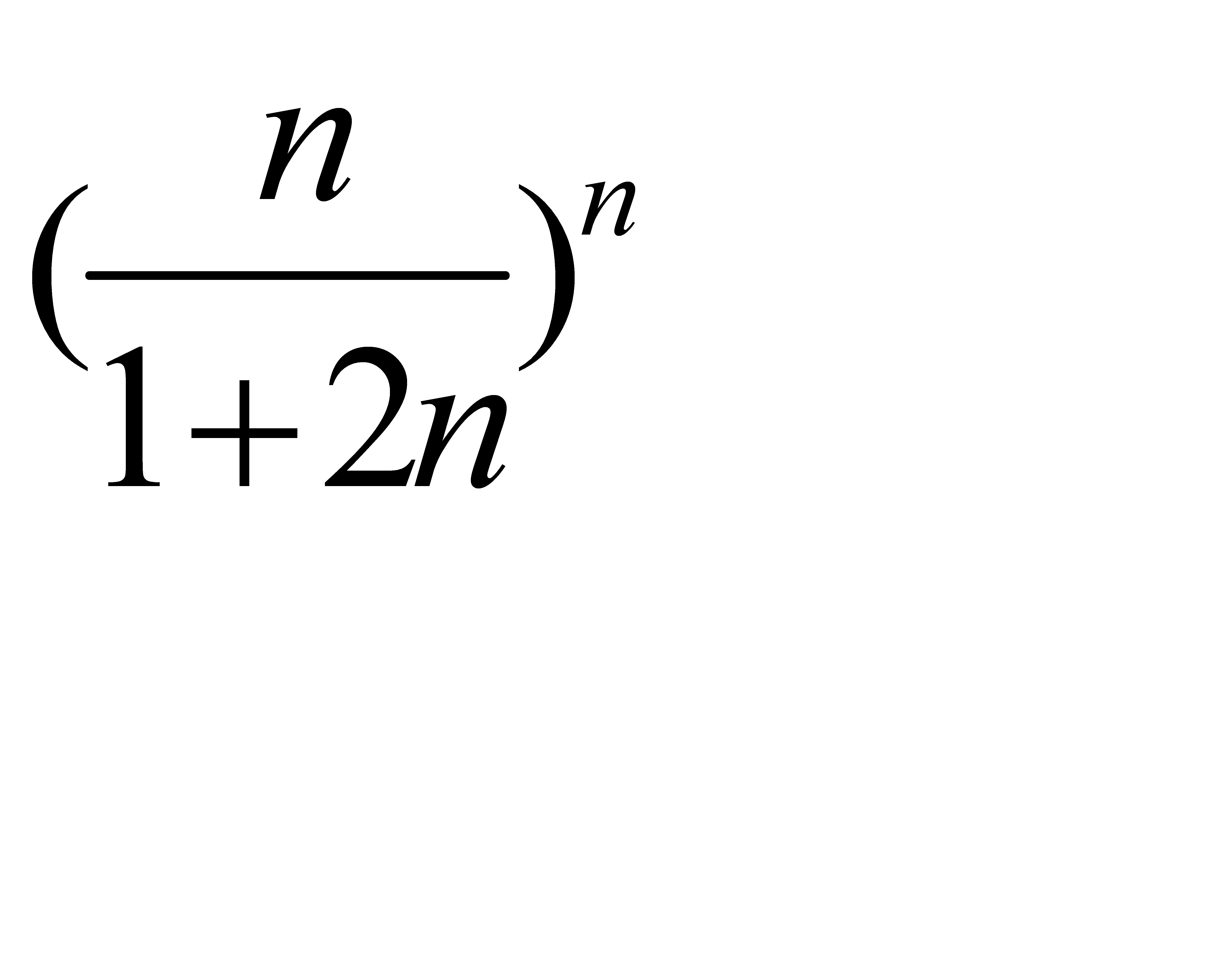 D)
D) 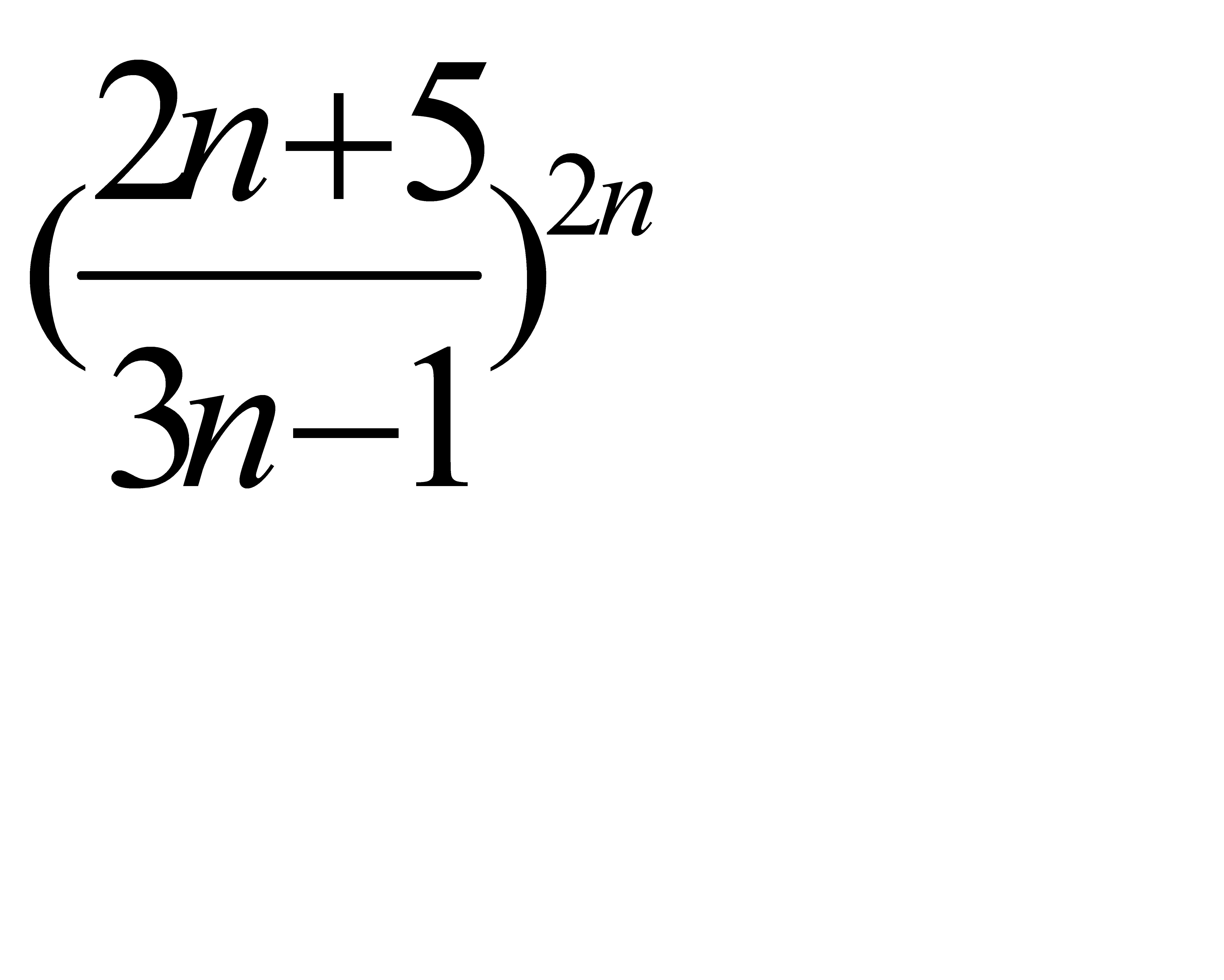 G)
G) 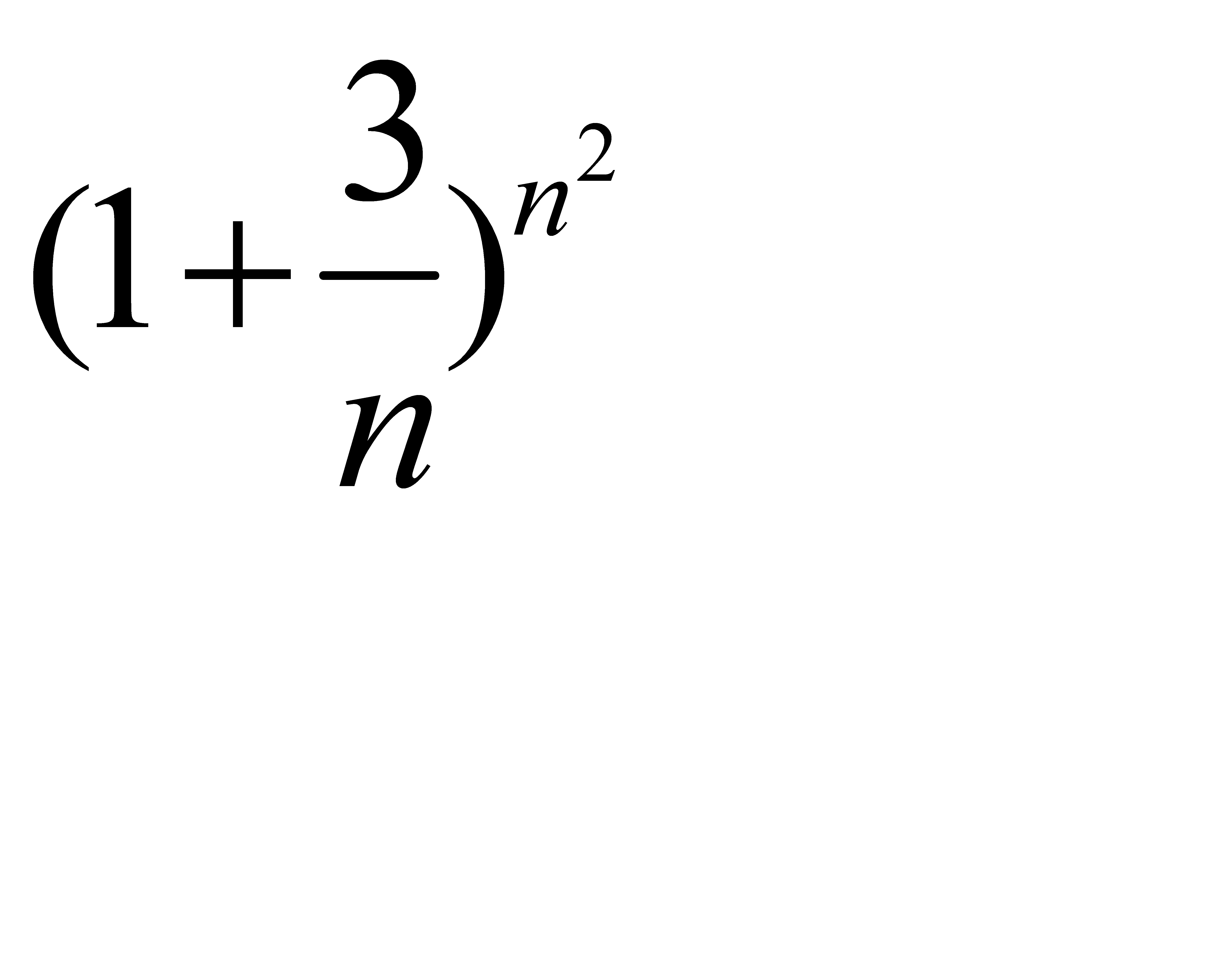
Жинақтылыққа Лейбниц белгісімен зерттелетін қатардың жалпы мүшесі: B) 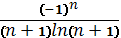 D)
D) 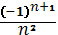 F)
F) 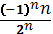
Жинақтылыққа салыстыру белгісімен зерттелетін қатардың жалпы мүшесі:B) 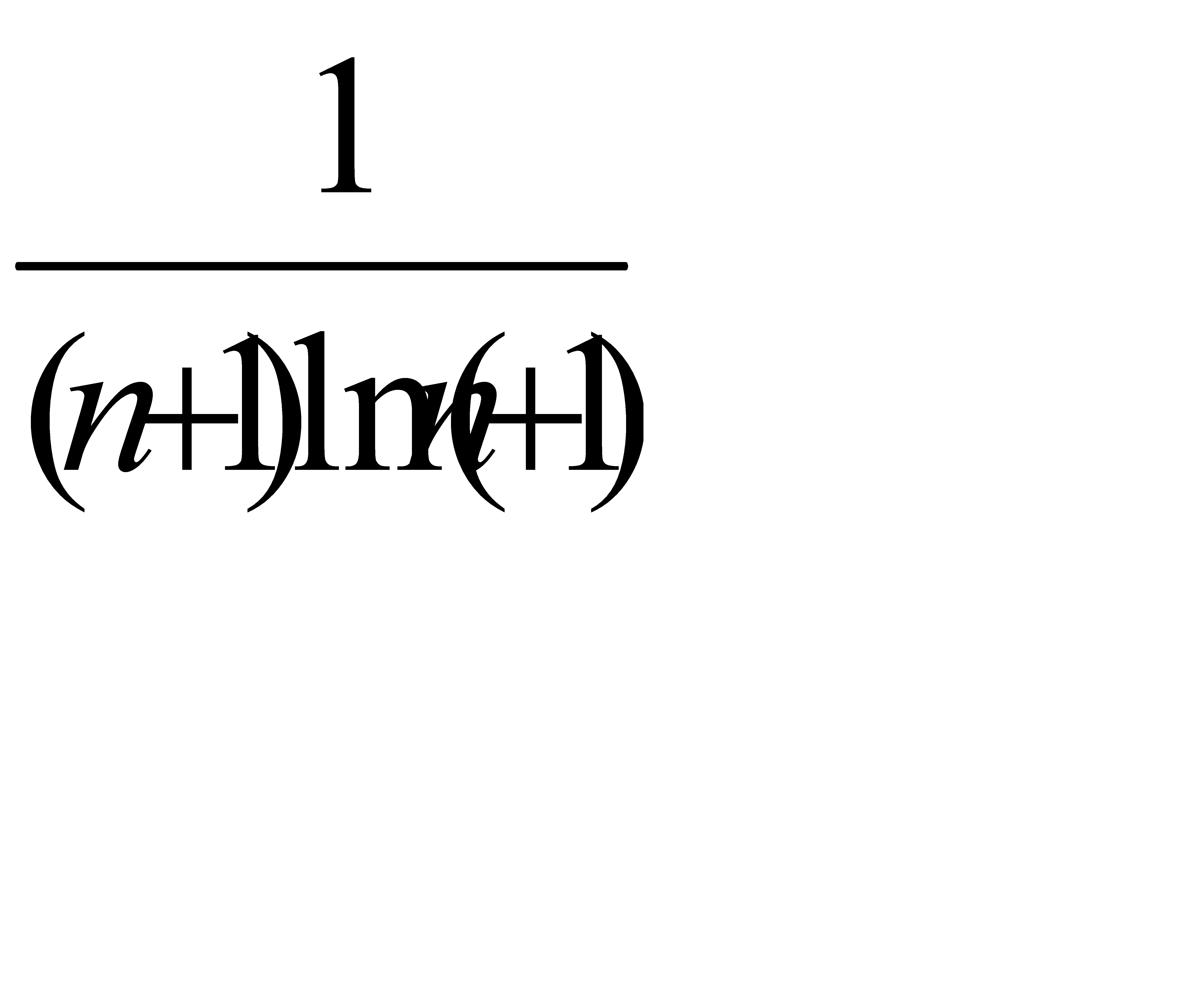 D)
D) 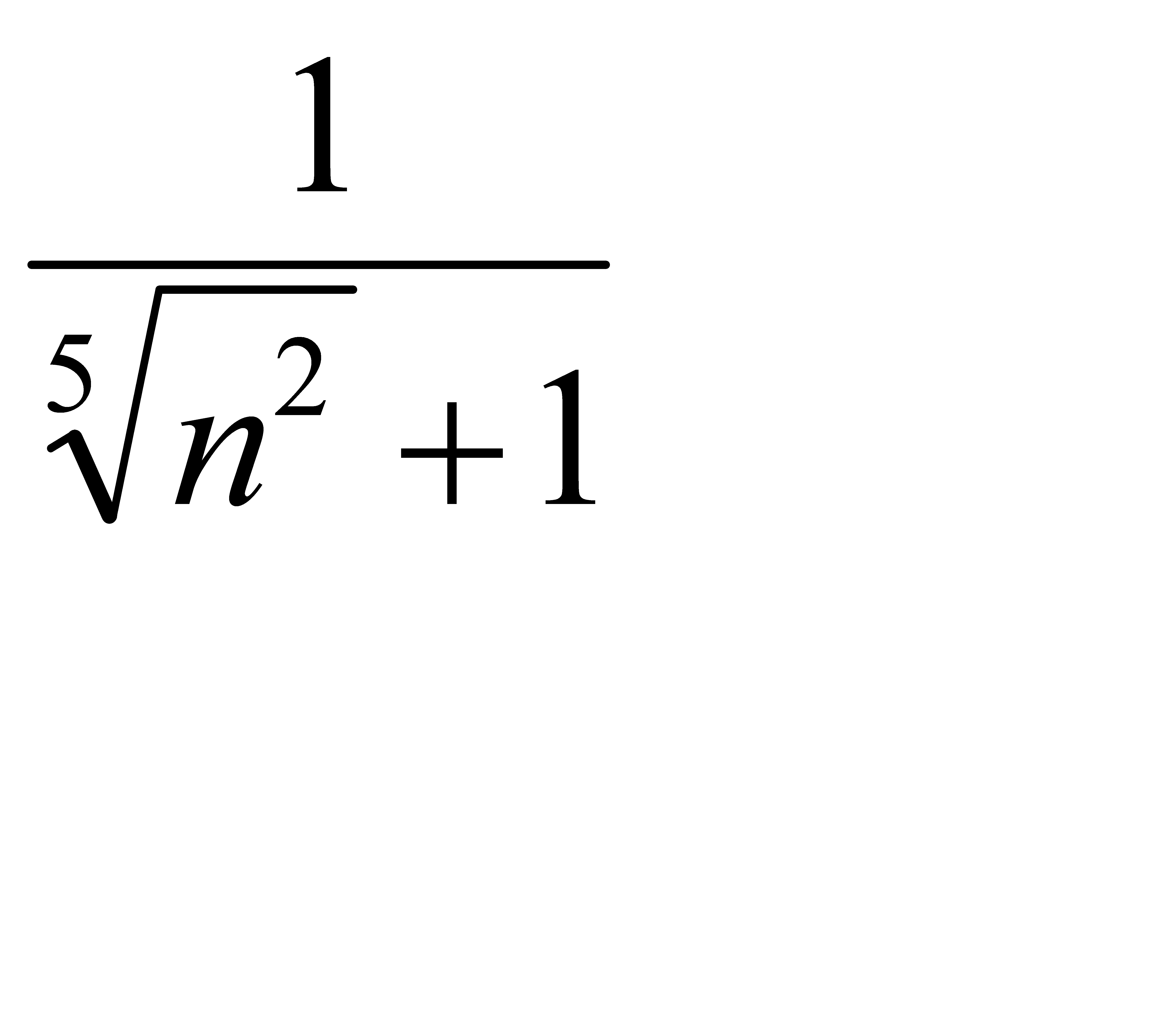 E)
E) 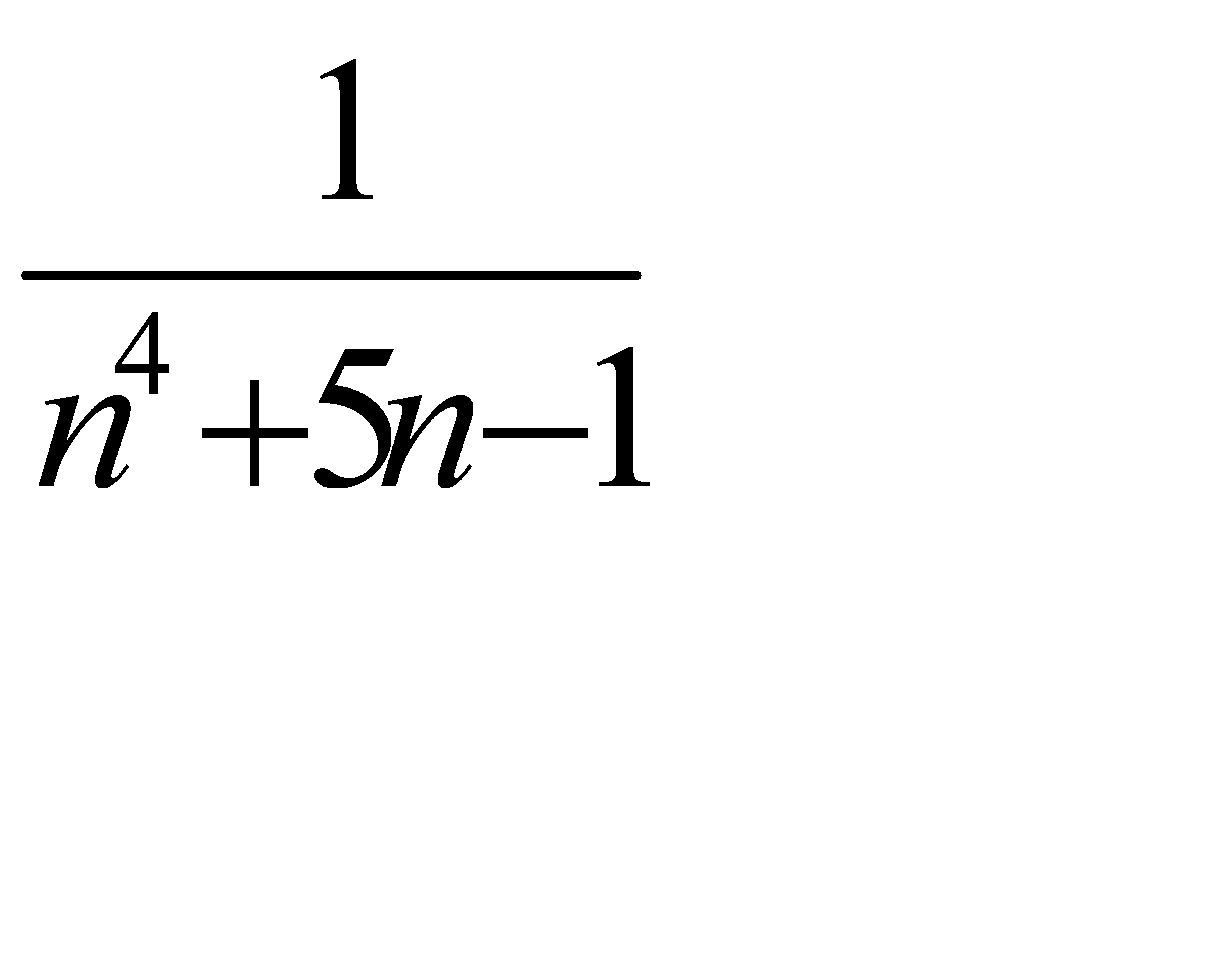
Жинақтылықтың қажетті белгісі орындалатын қатардың жалпы мүшесі: B) 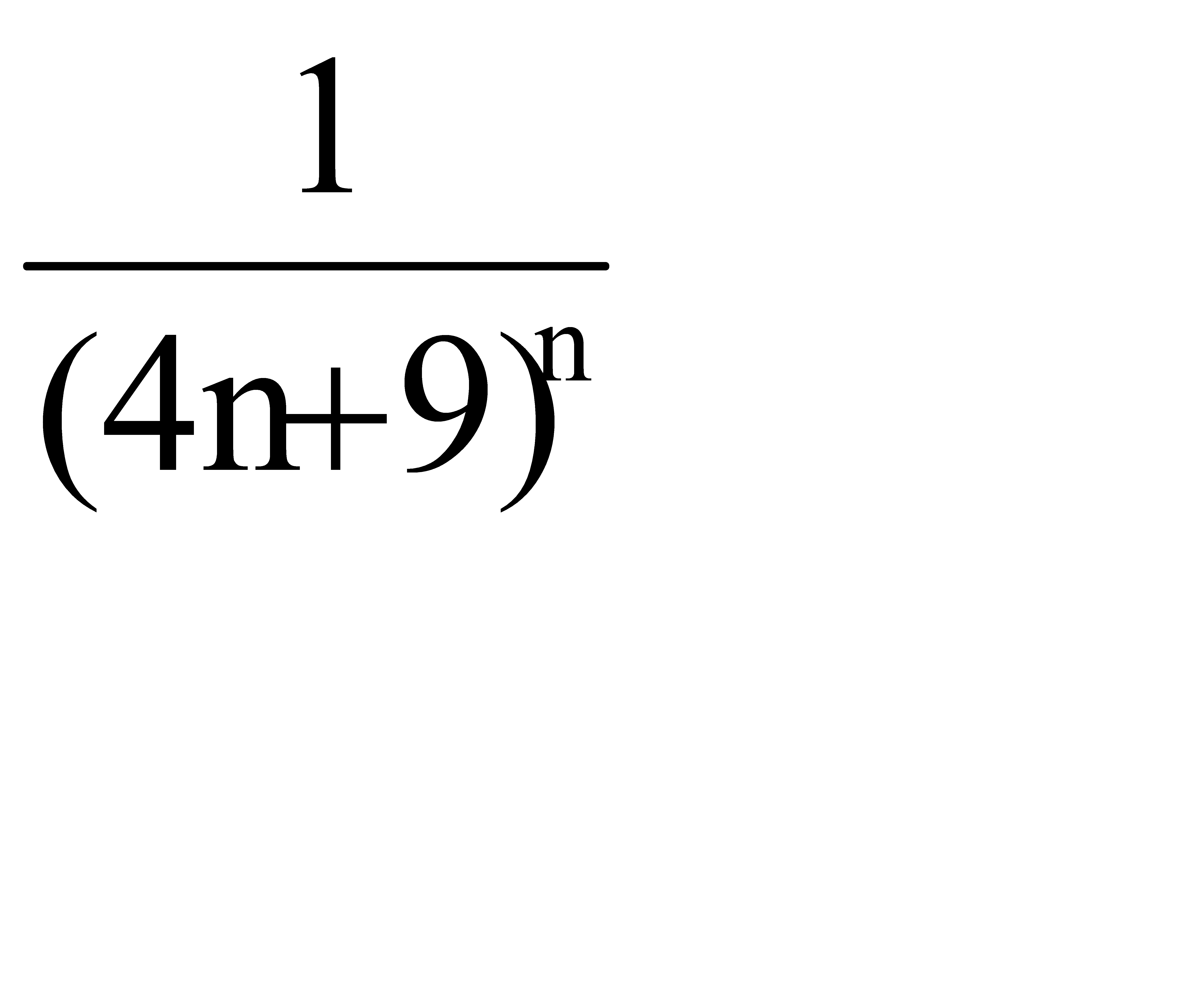 D)
D) 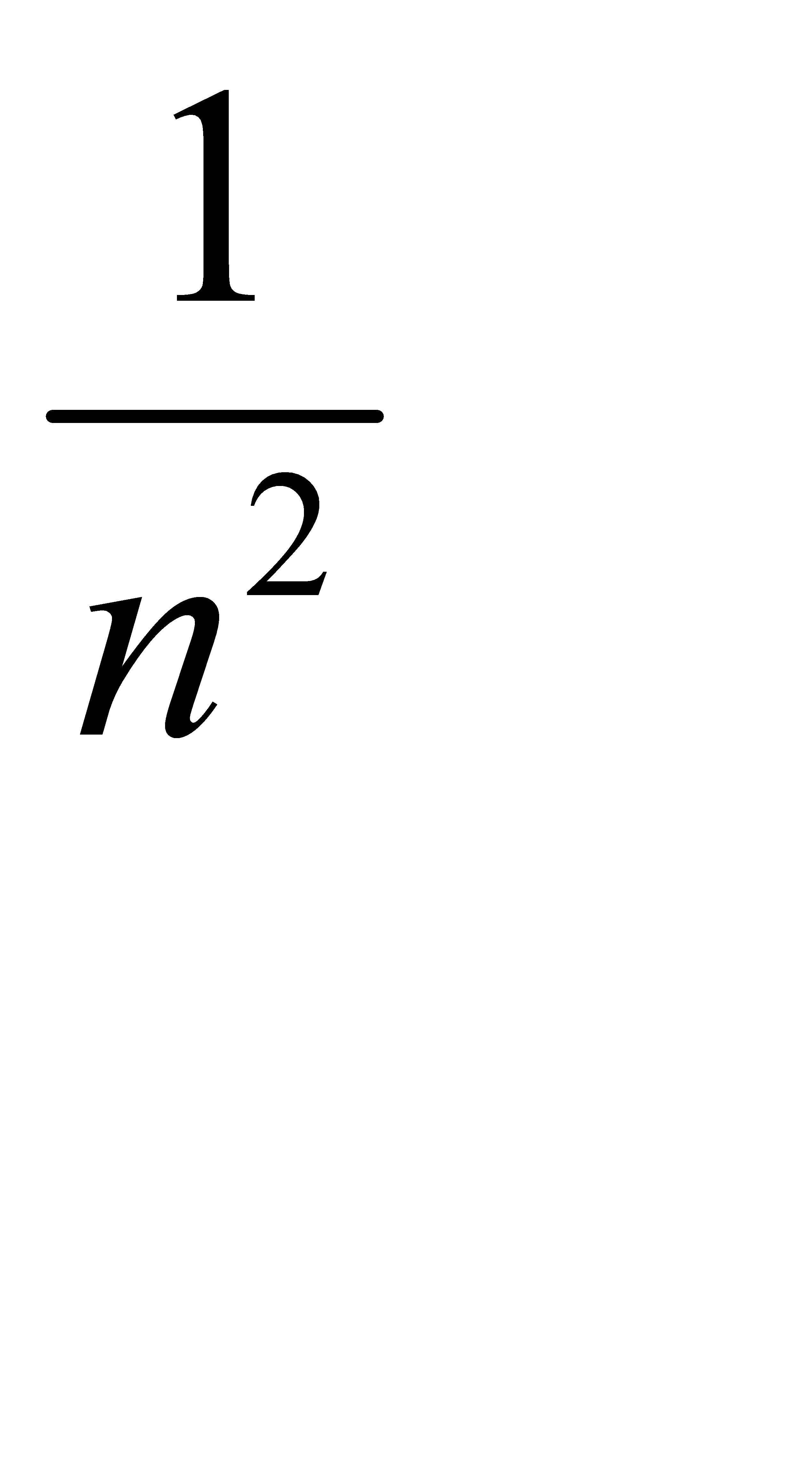 E)
E) 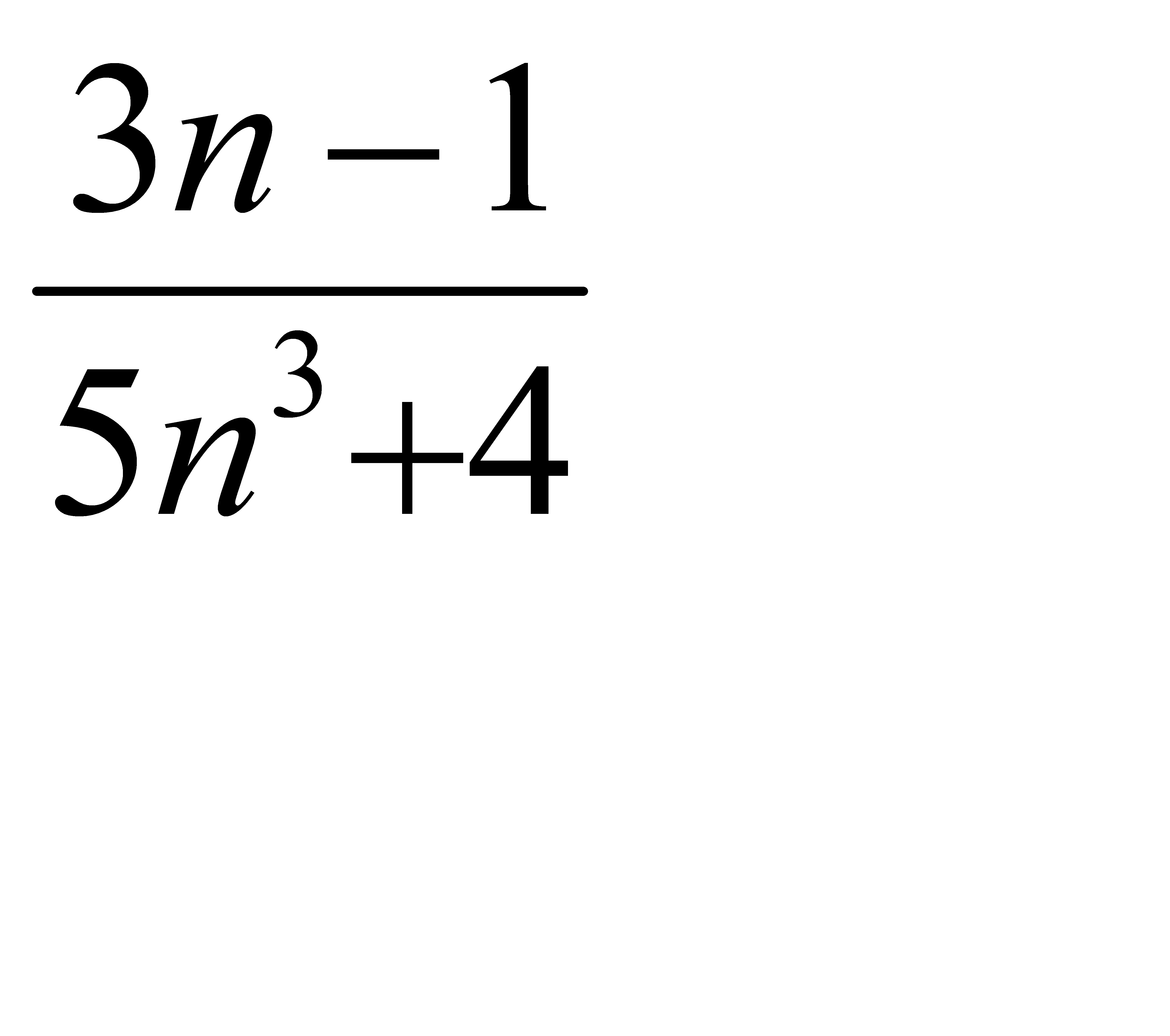
Жинақтылықтың қажетті белгісі орындалатын қатардың жалпы мүшесі:B) 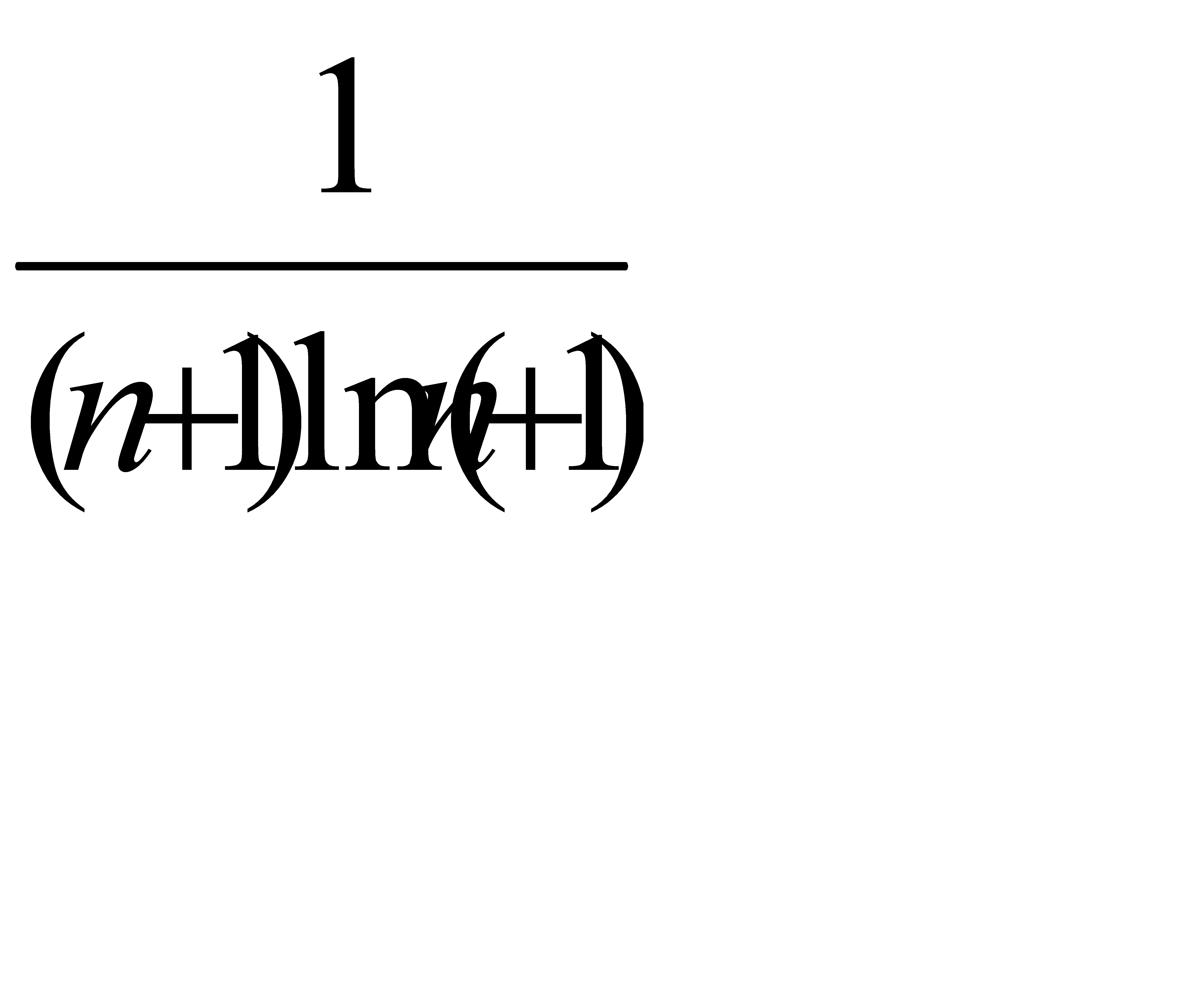 D)
D) 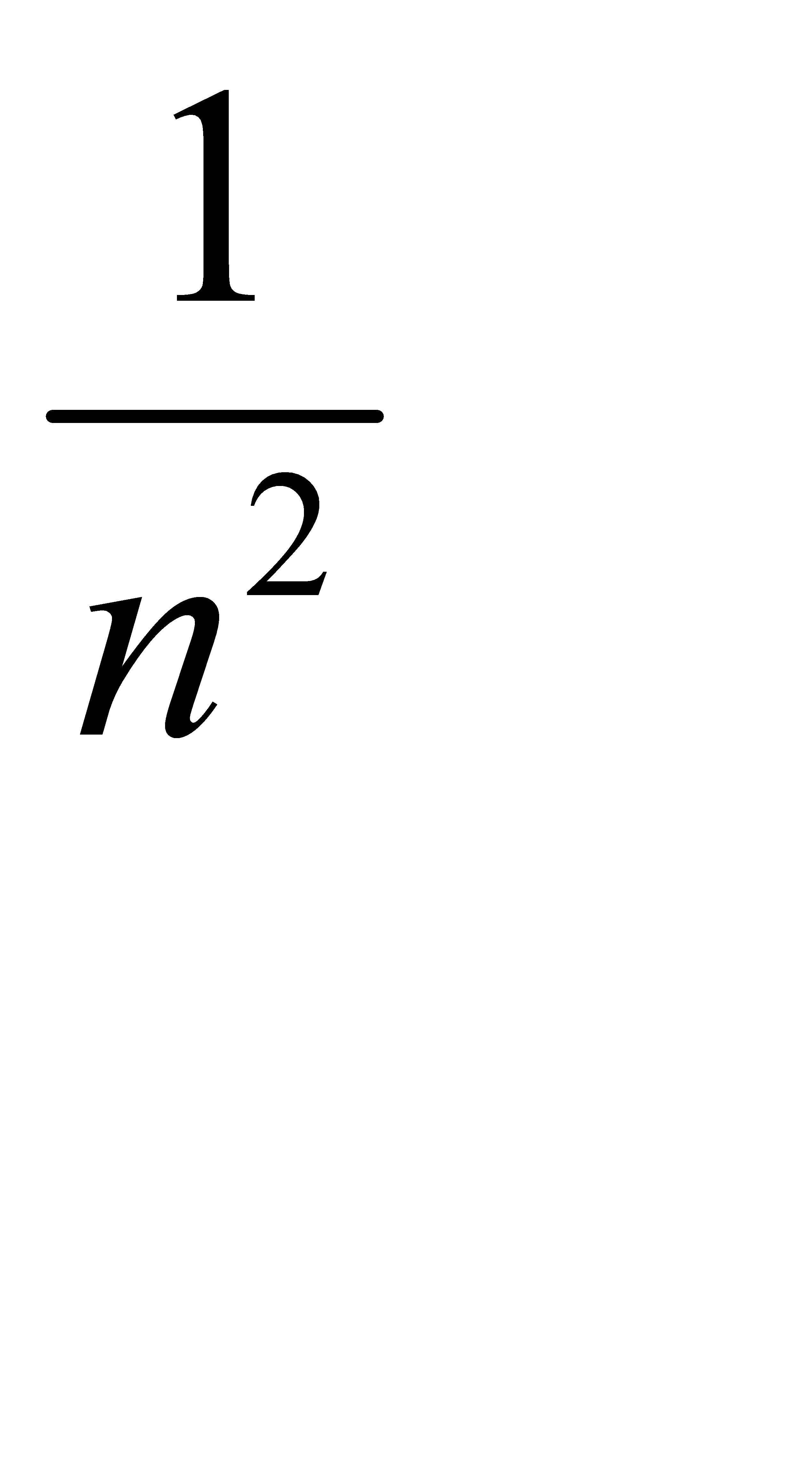 F)
F) 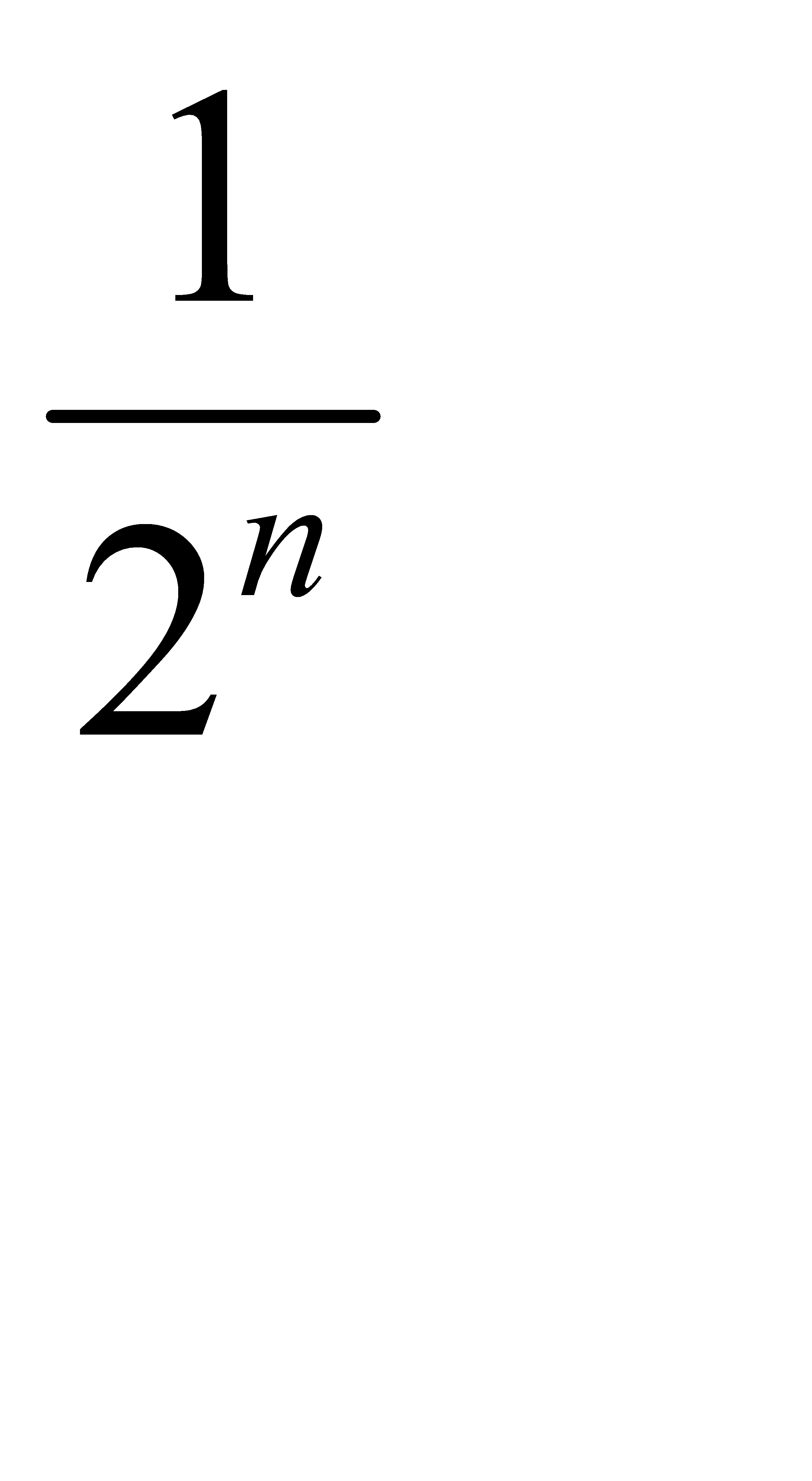
Интегралды есепте. 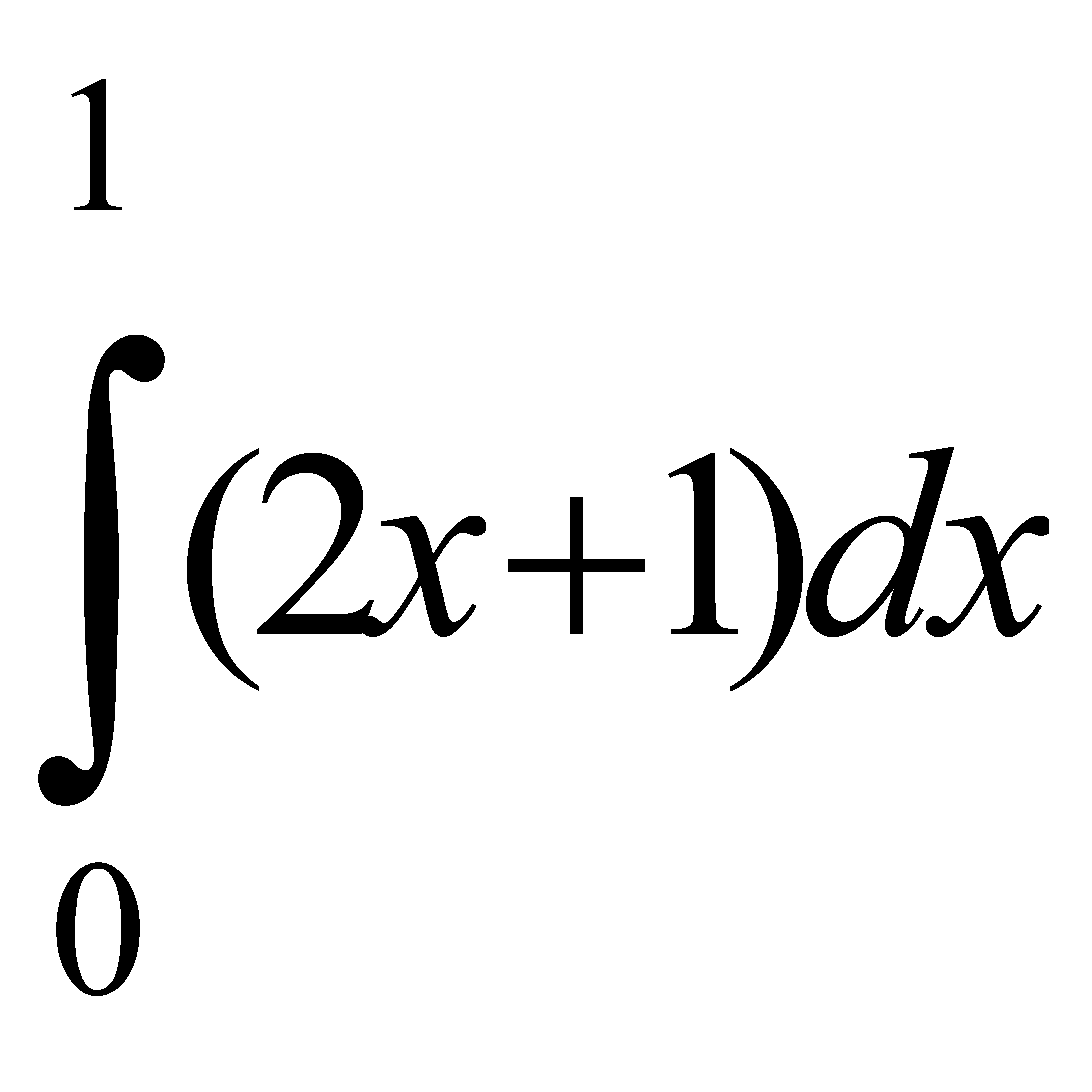 C) 2 E) 4/2 H) 6/3
C) 2 E) 4/2 H) 6/3
Интегралды есепте. 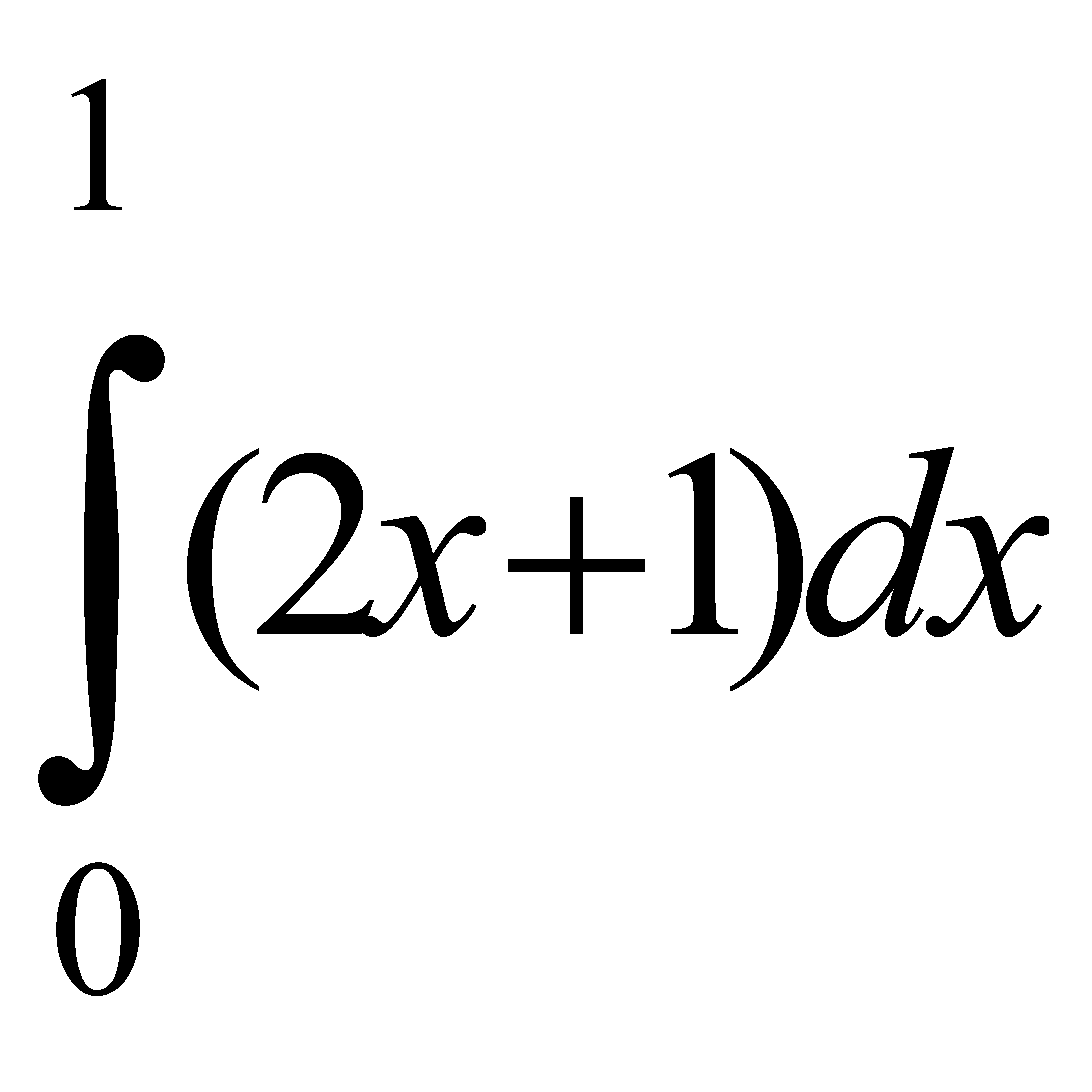 C) 2 E) 4/2 H) 6/3
C) 2 E) 4/2 H) 6/3
Интегралды есепте:  мұндағы -
мұндағы -  аймағы
аймағы  .A) 9/20 D)
.A) 9/20 D) 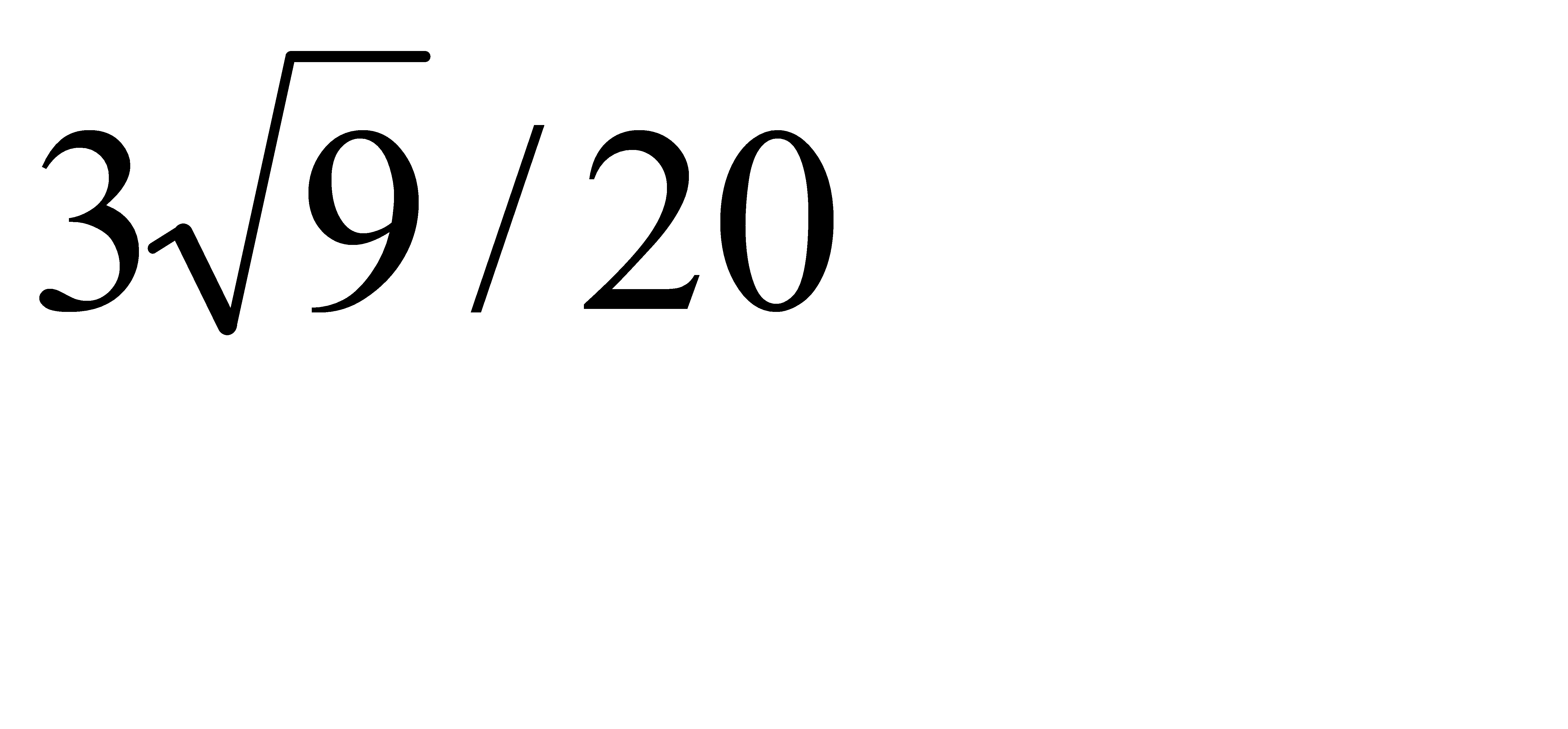 F)
F) 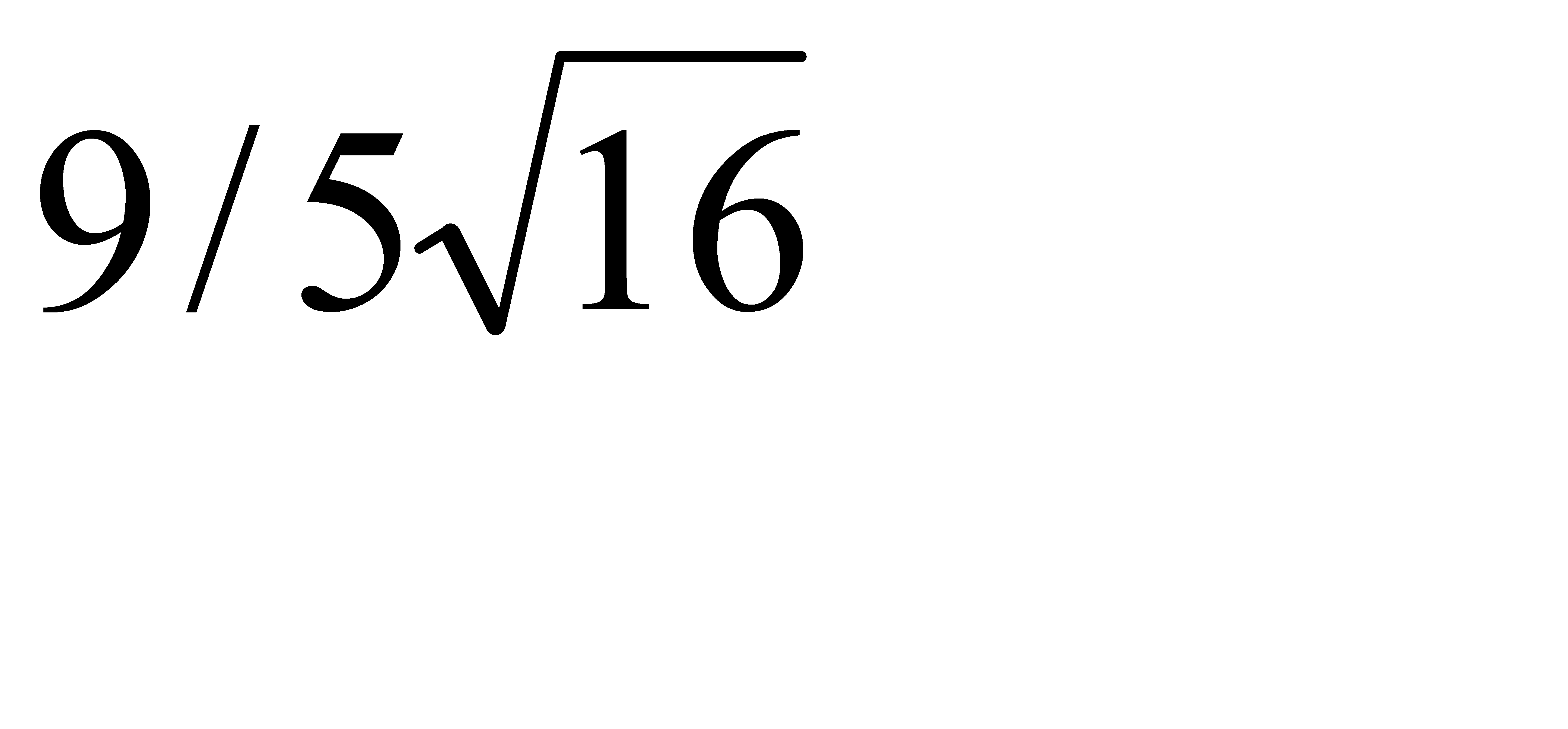
Интегралды есепте: 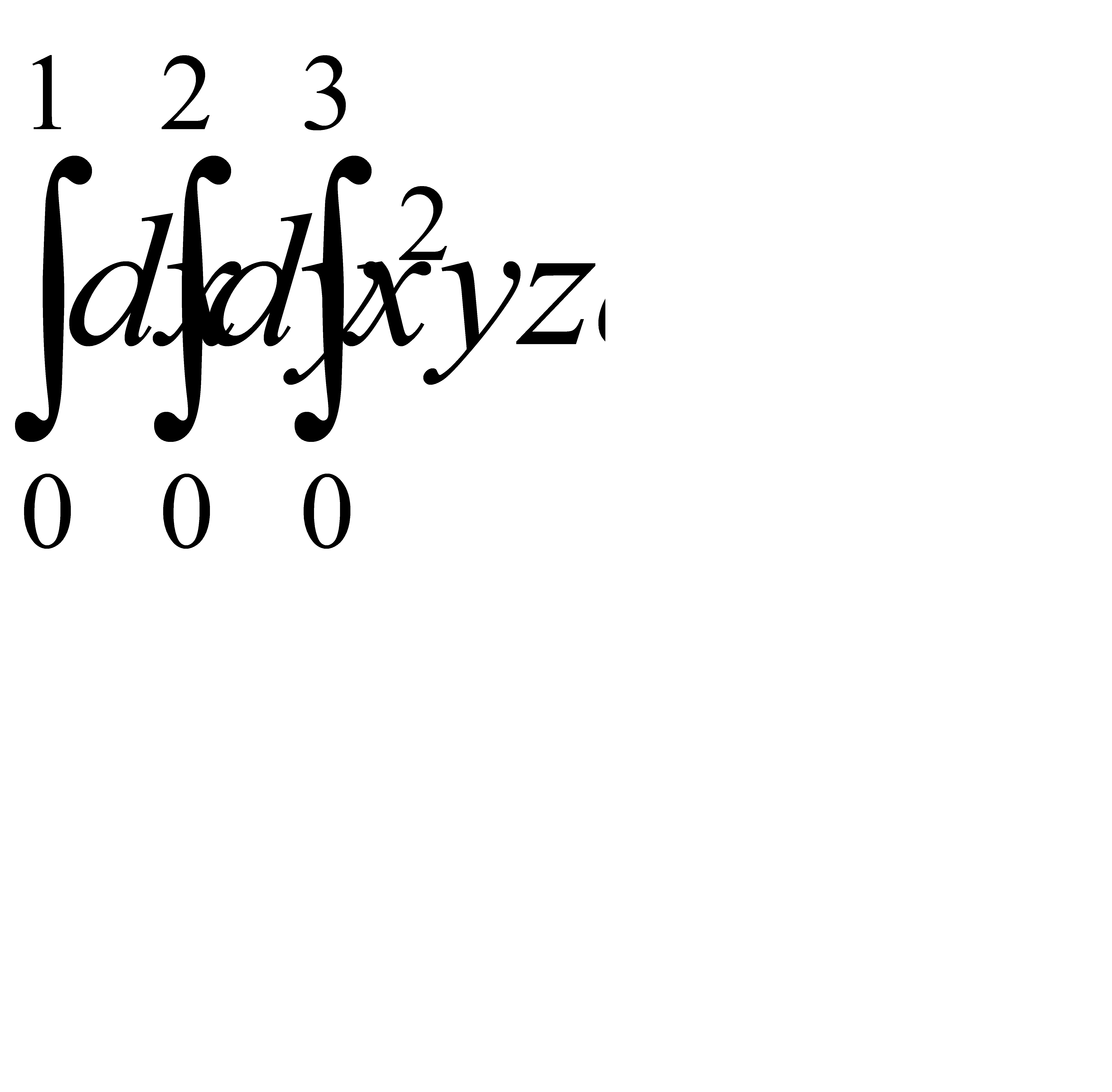 : C) 3 F) 6/2 H) 9/3
: C) 3 F) 6/2 H) 9/3
Интегралды есепте: 24  D) 1 G) 2/2 H) 8/8
D) 1 G) 2/2 H) 8/8
Интегралды есепте:  3
3 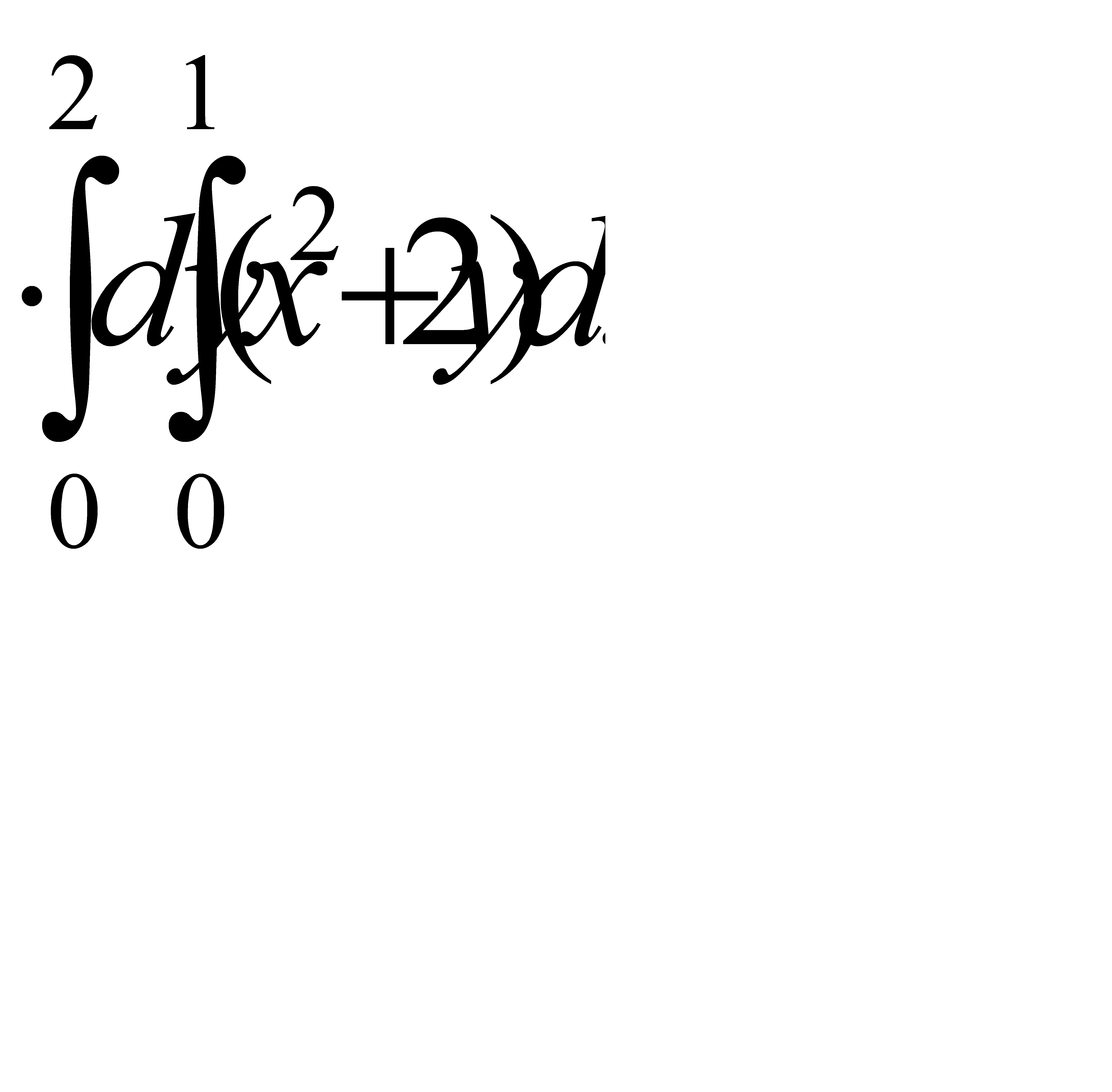 A) 14 D) 28/2 G) 42/3
A) 14 D) 28/2 G) 42/3
Интегралды есепте:  3
3 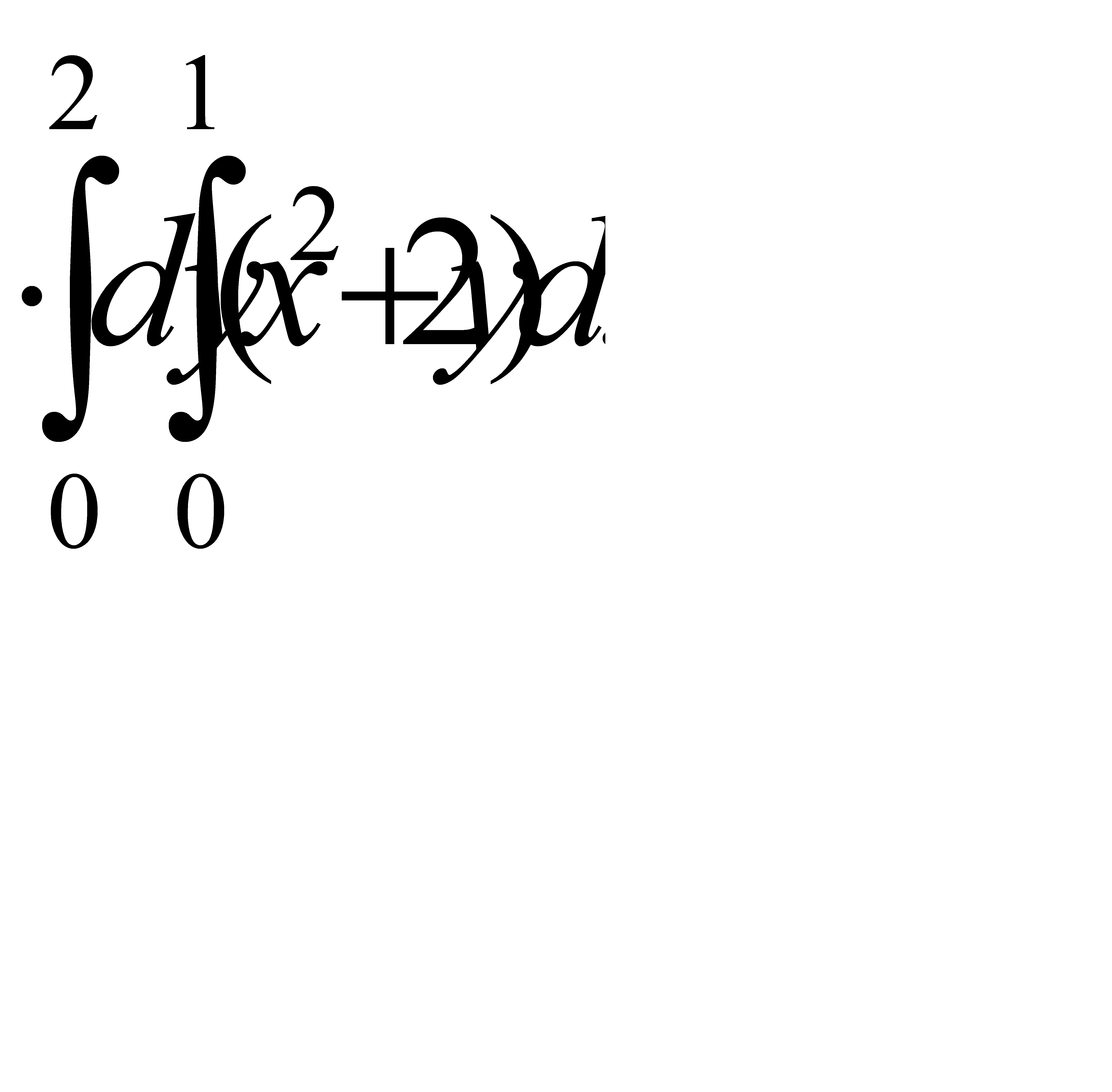 A) 14 D) 28/2 G) 42/3
A) 14 D) 28/2 G) 42/3
Интегралды есепте: 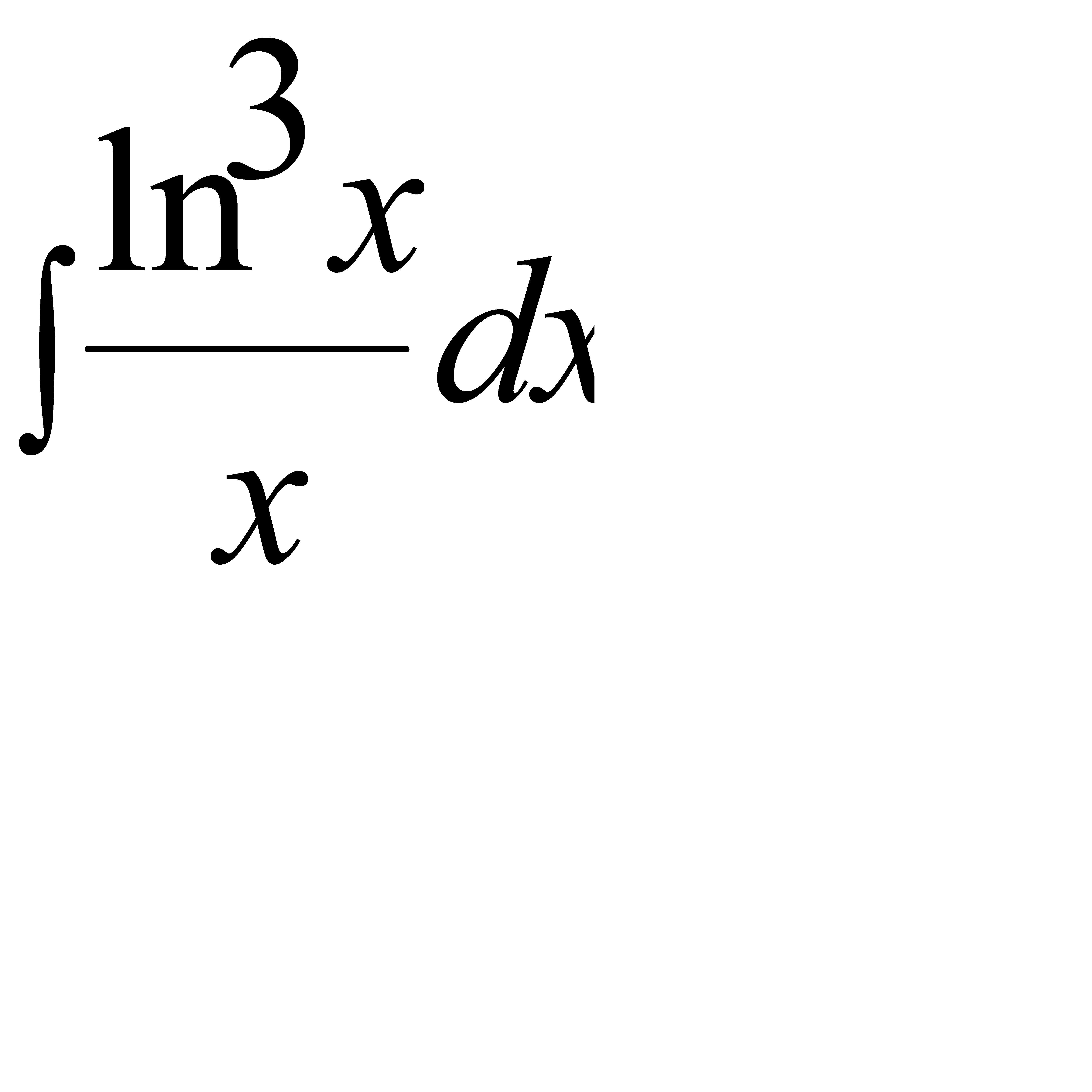 A)
A) 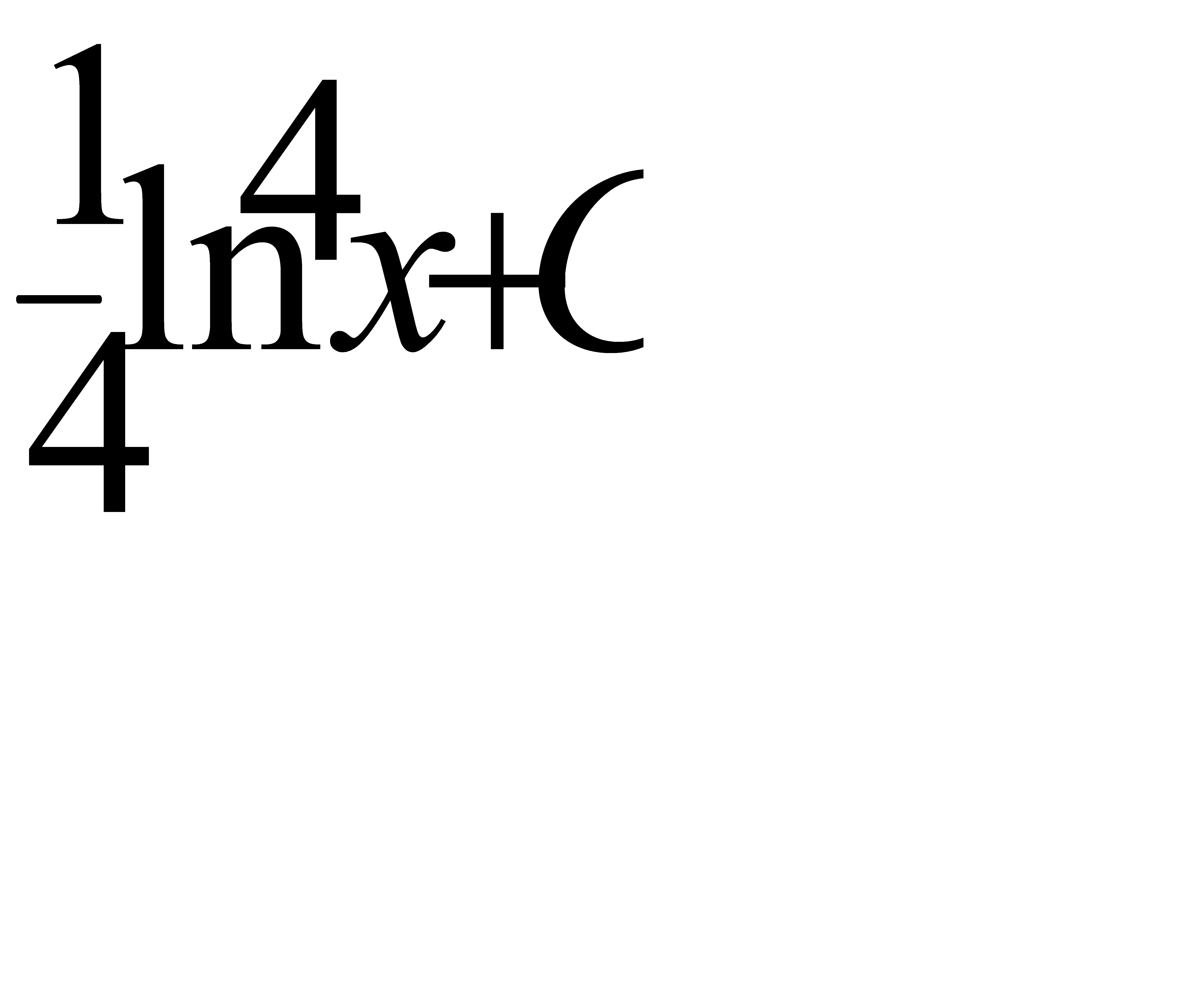 G)
G) 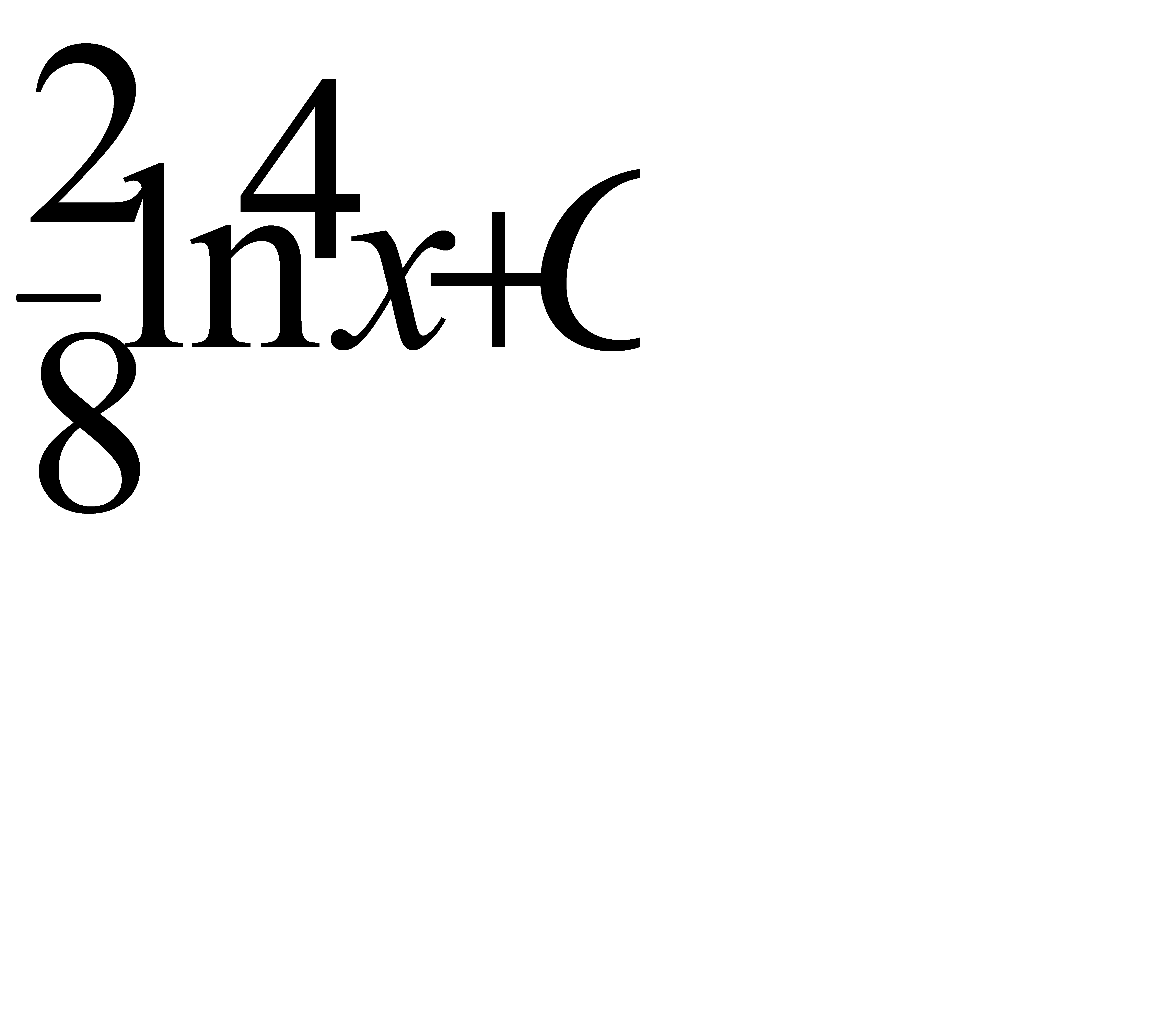 H)
H) 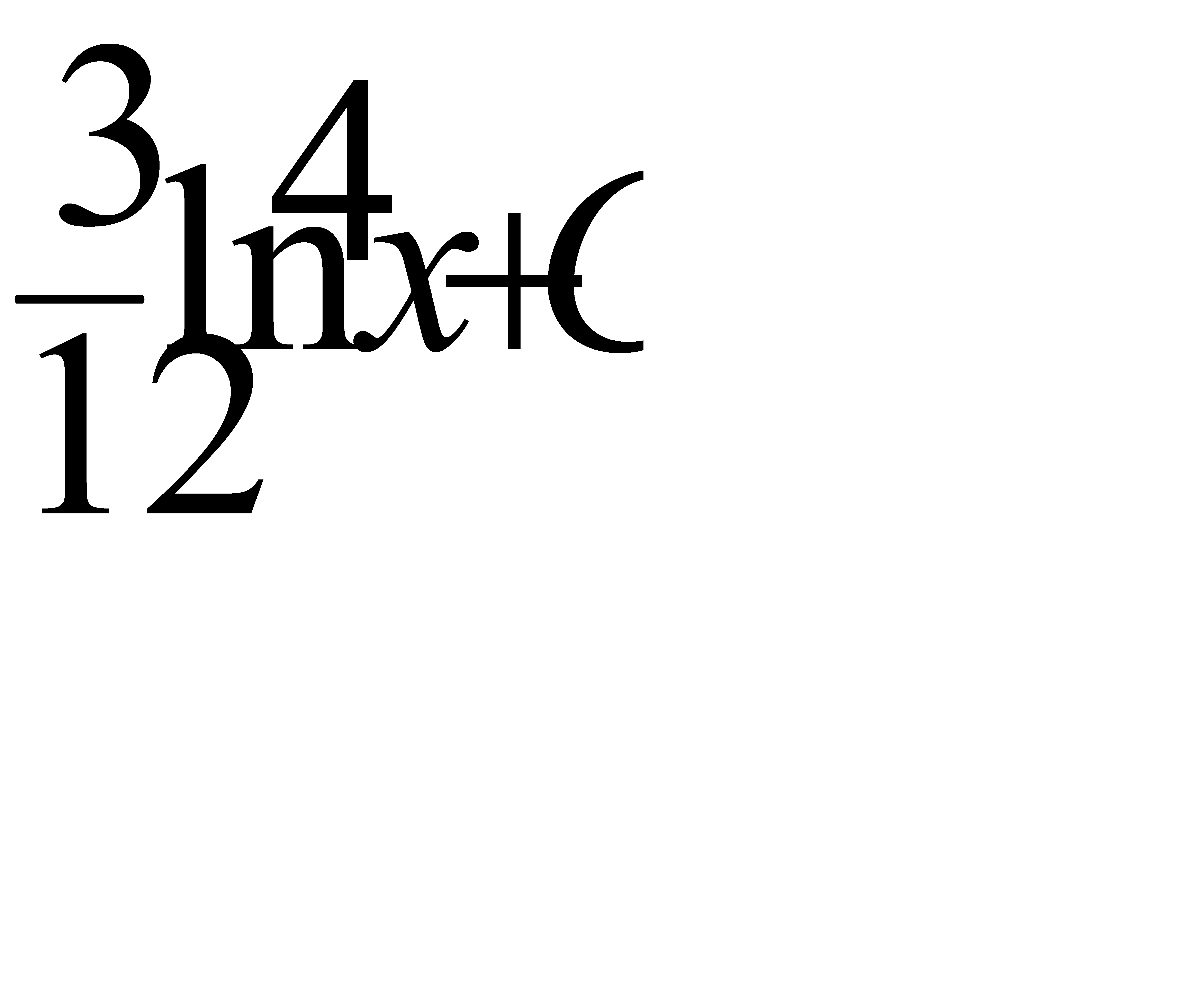
Интегралды есепте:
| ( |
| ) |
| dx: |
| y |
| x |
| dy |
| ò |
| ò |
| + |
Интегралды есепте:
| ò |
| ò |
| ò |
| Dz; |
| z |
| xy |
| dy |
| dx |
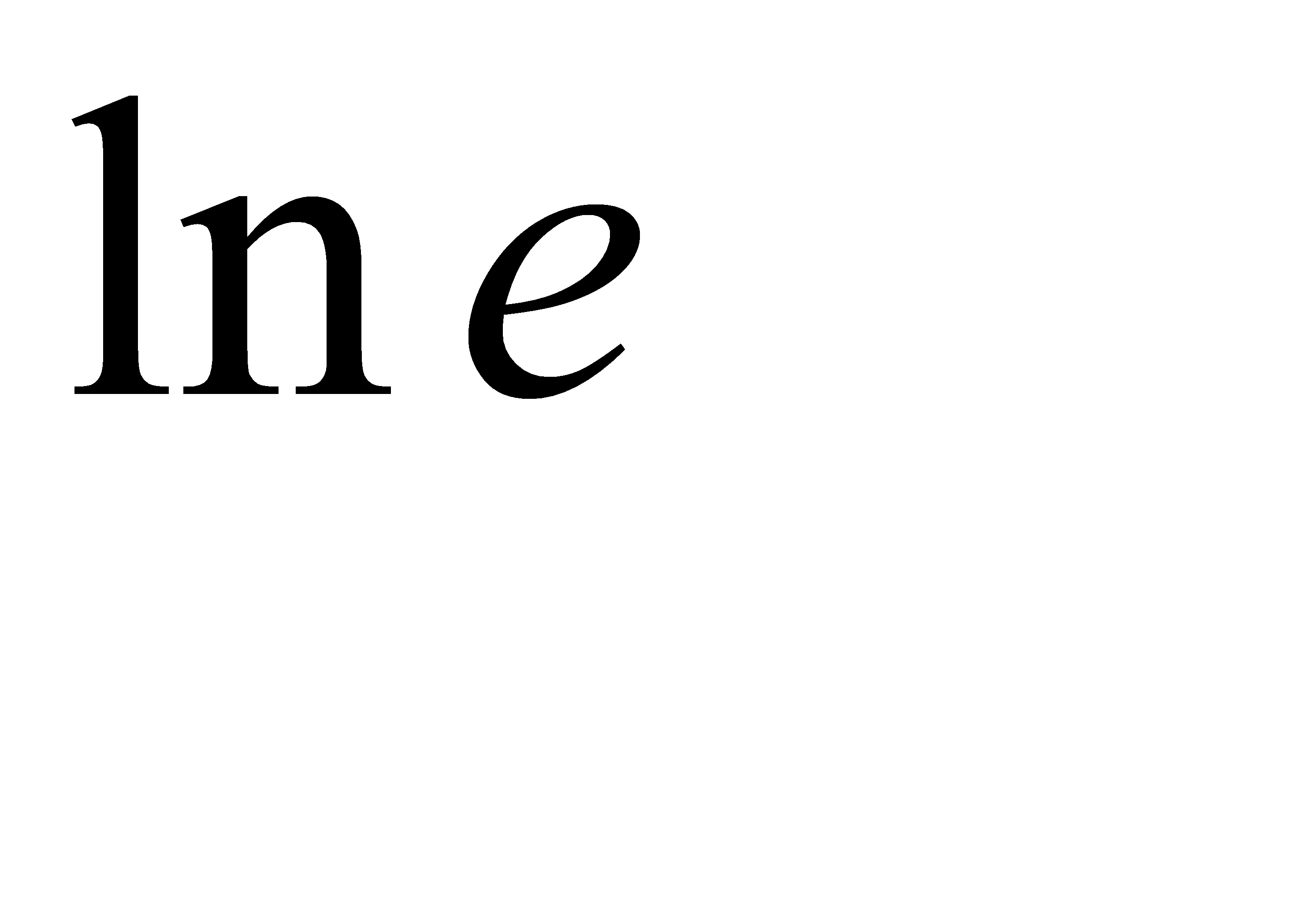 G)
G) 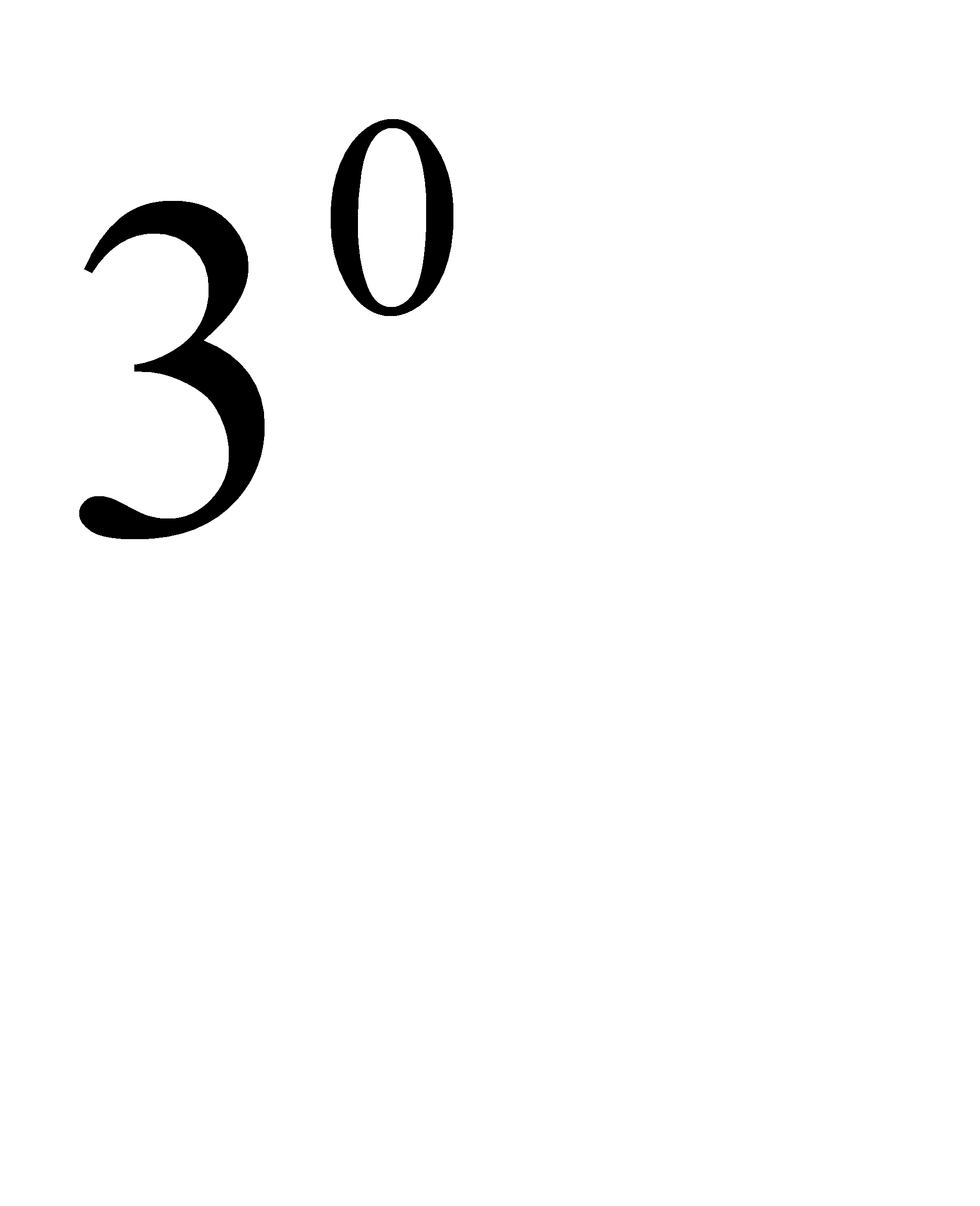
Интегралды есепте:
| ( |
| ) |
| dy: |
| y |
| x |
| dx |
| ò |
| ò |
| + |
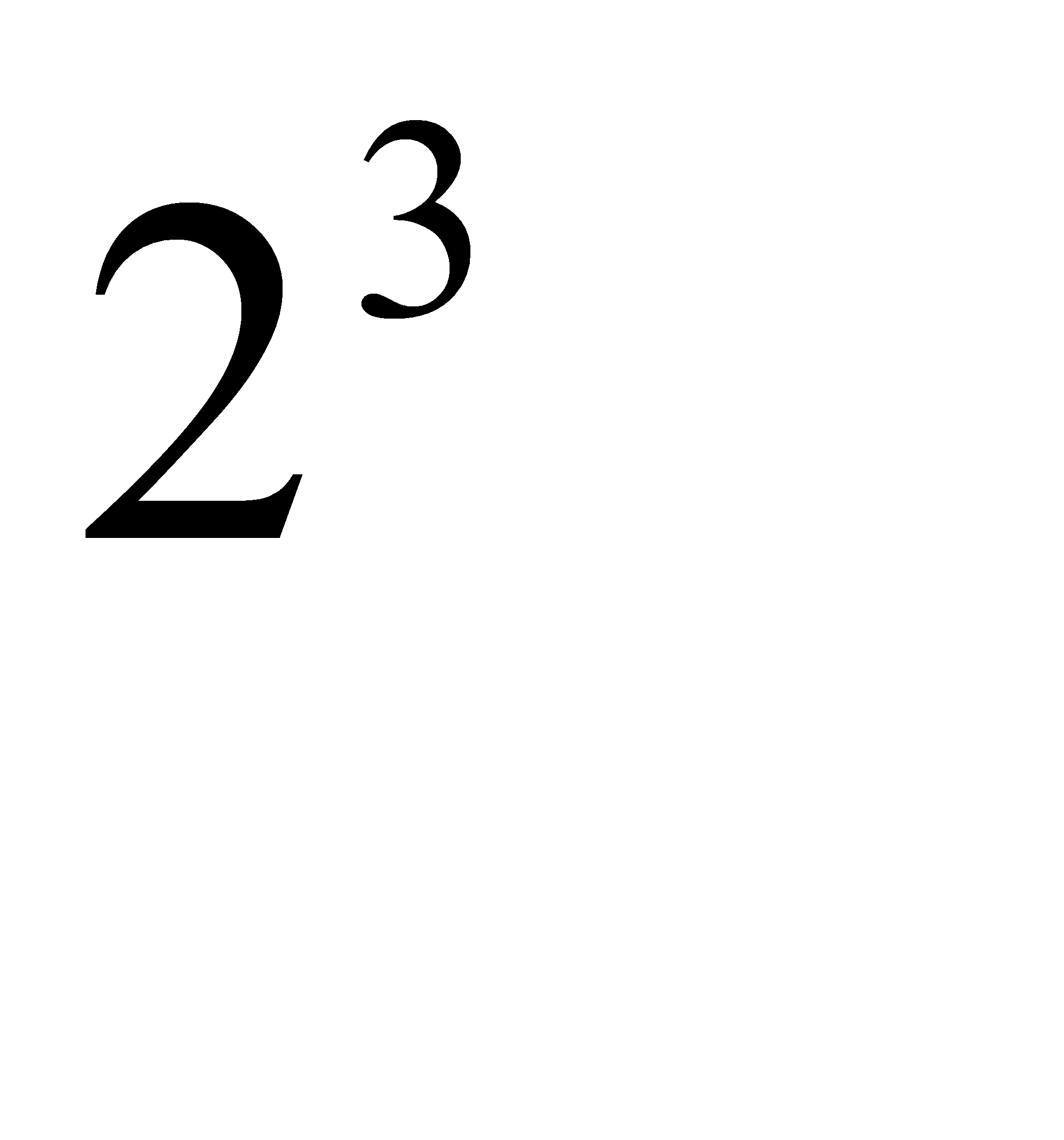 E) 16/2
E) 16/2
Интегралды есепте:
| ò |
| ò |
| x |
| xydy |
| dx |
Интегралды есепте: 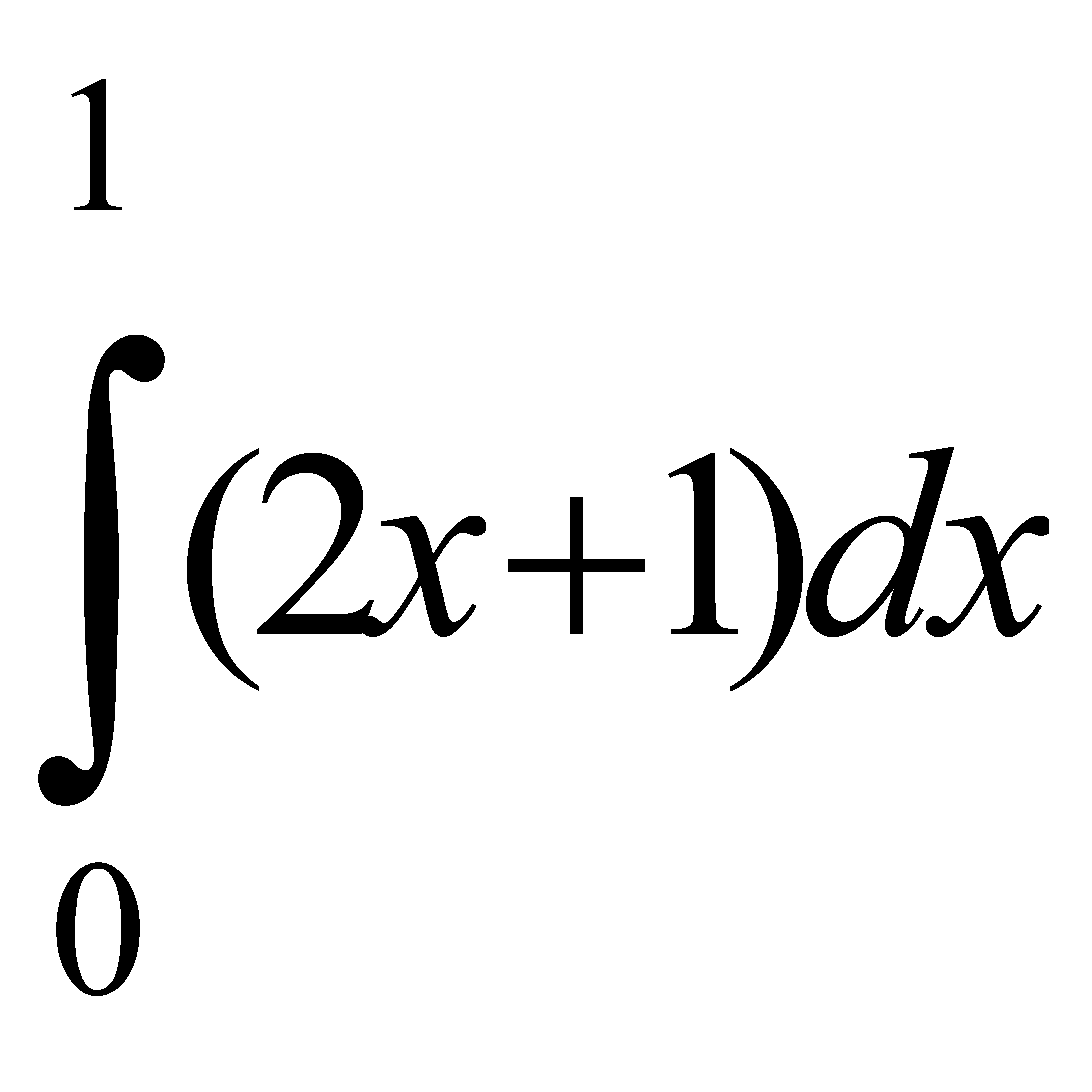 C) 2 E) 20 2 H)
C) 2 E) 20 2 H) 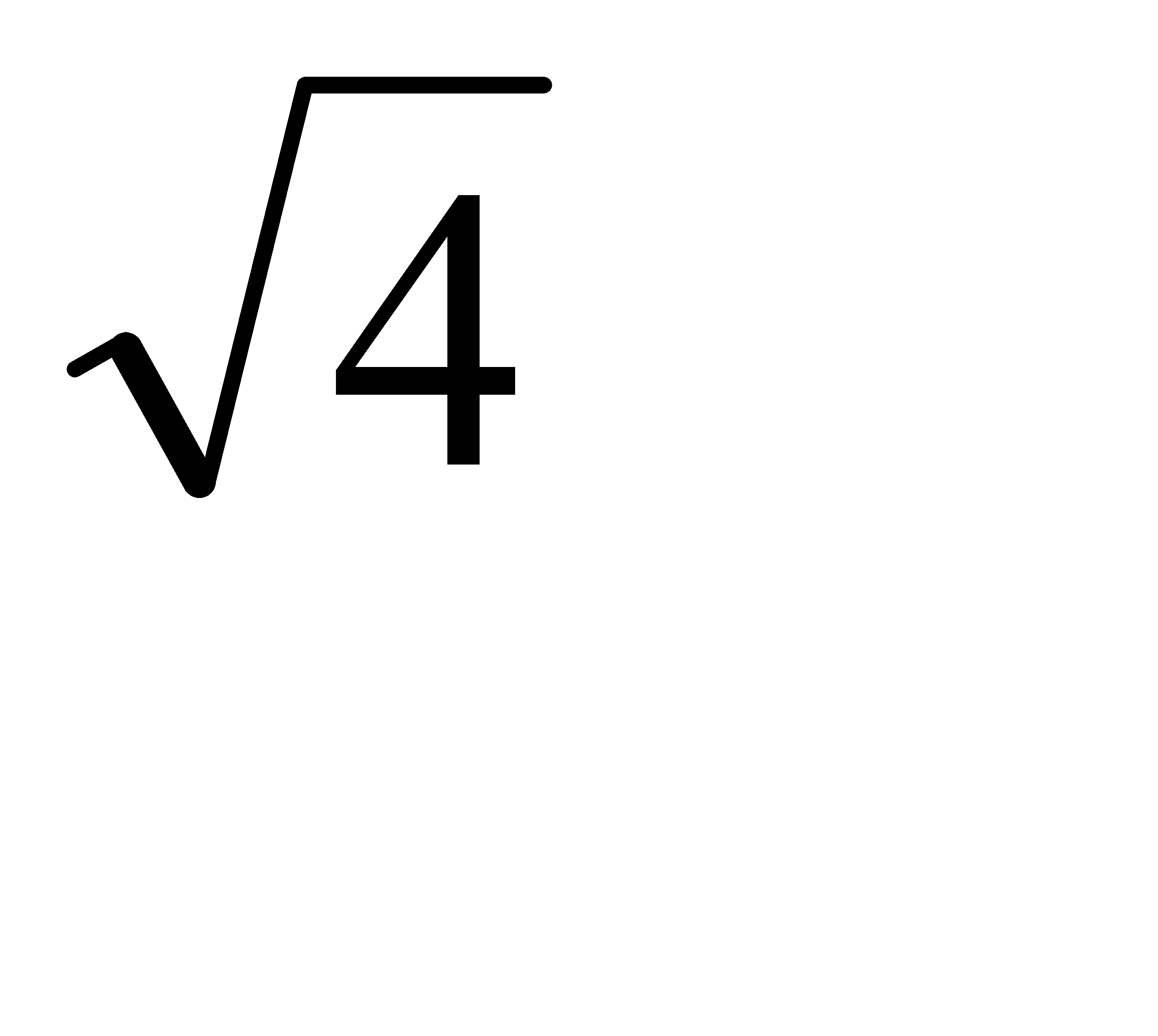
Интегралды есепте: 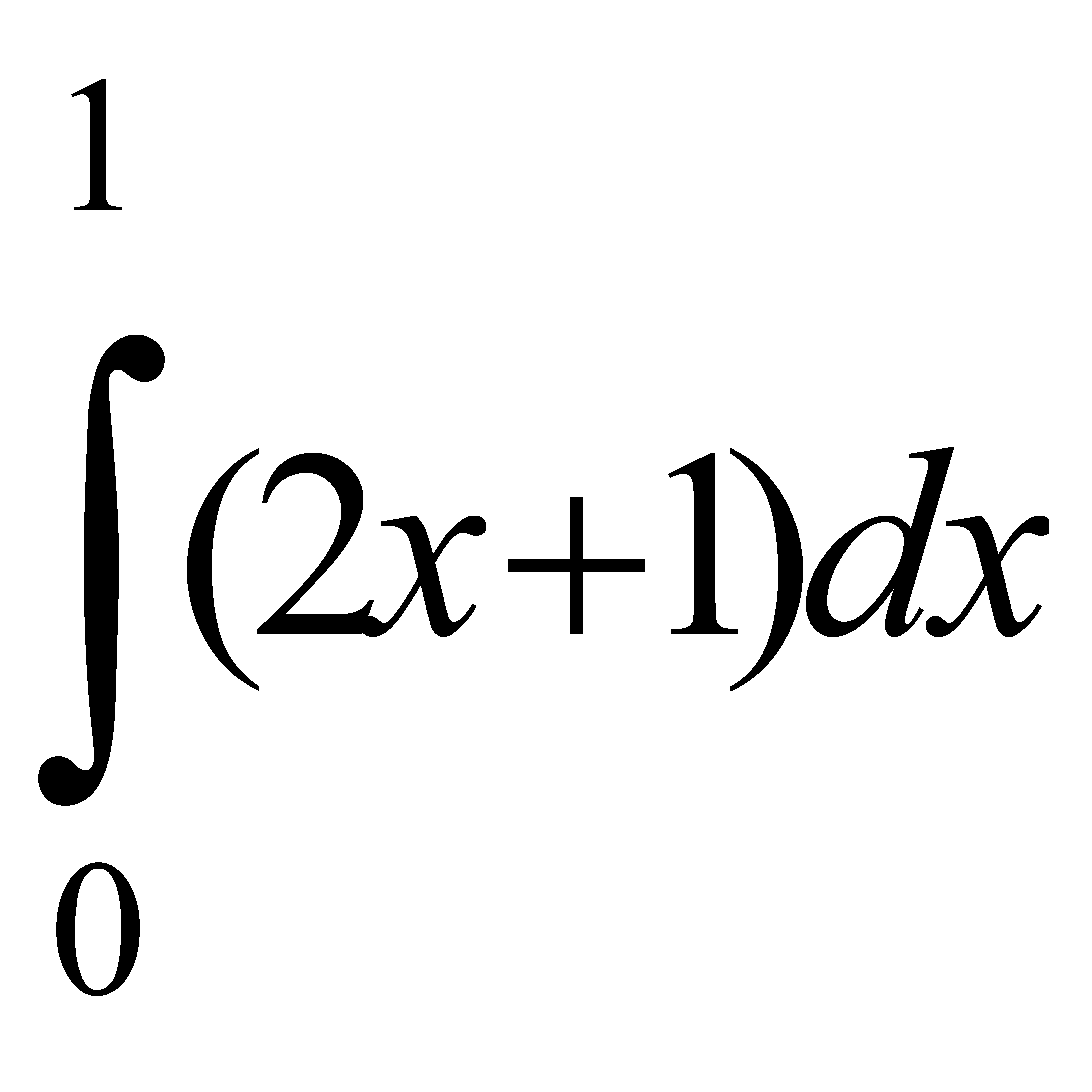 C) 2 E) 20 2 H)
C) 2 E) 20 2 H) 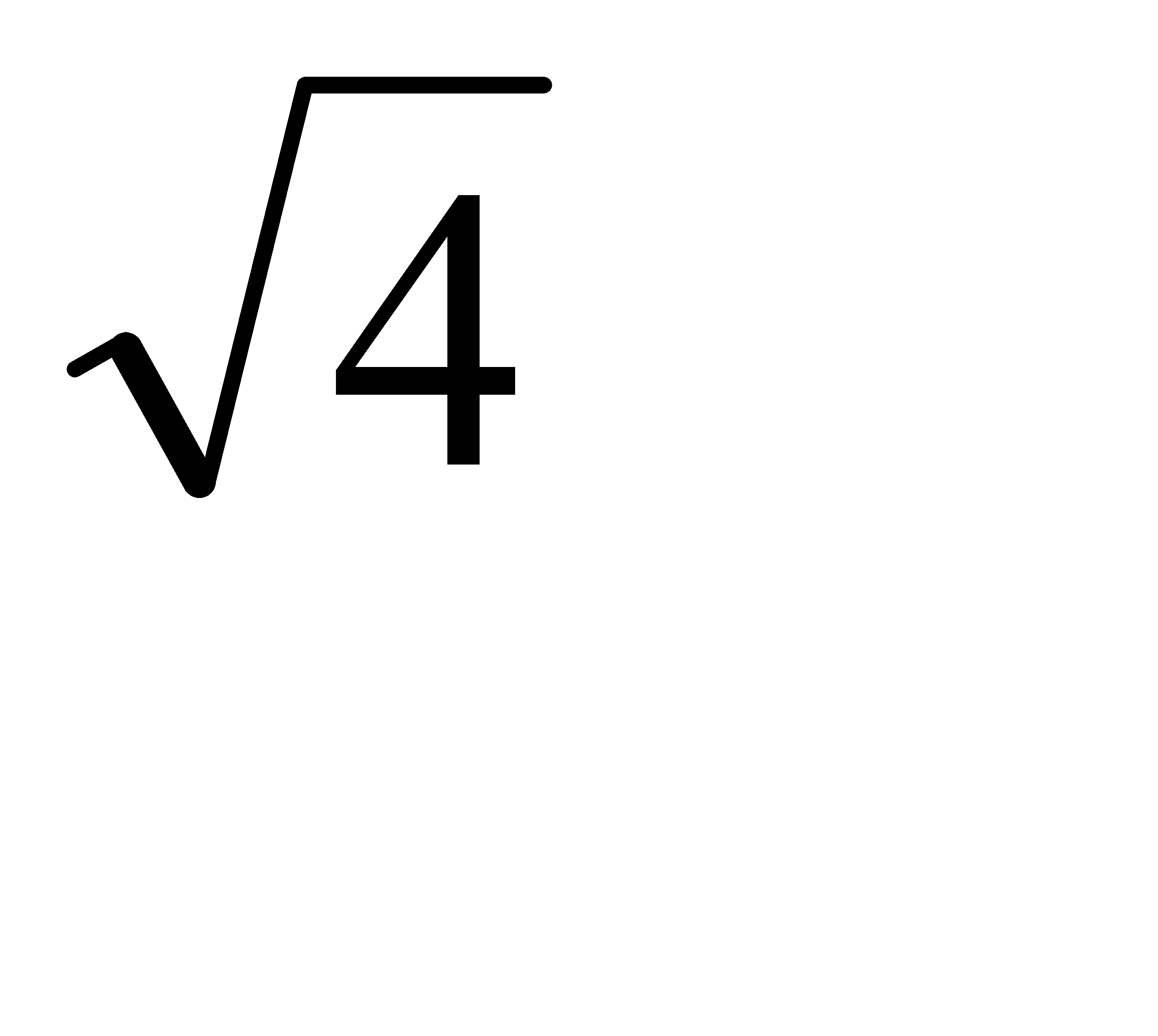
Интегралды есепте:  .A)
.A) 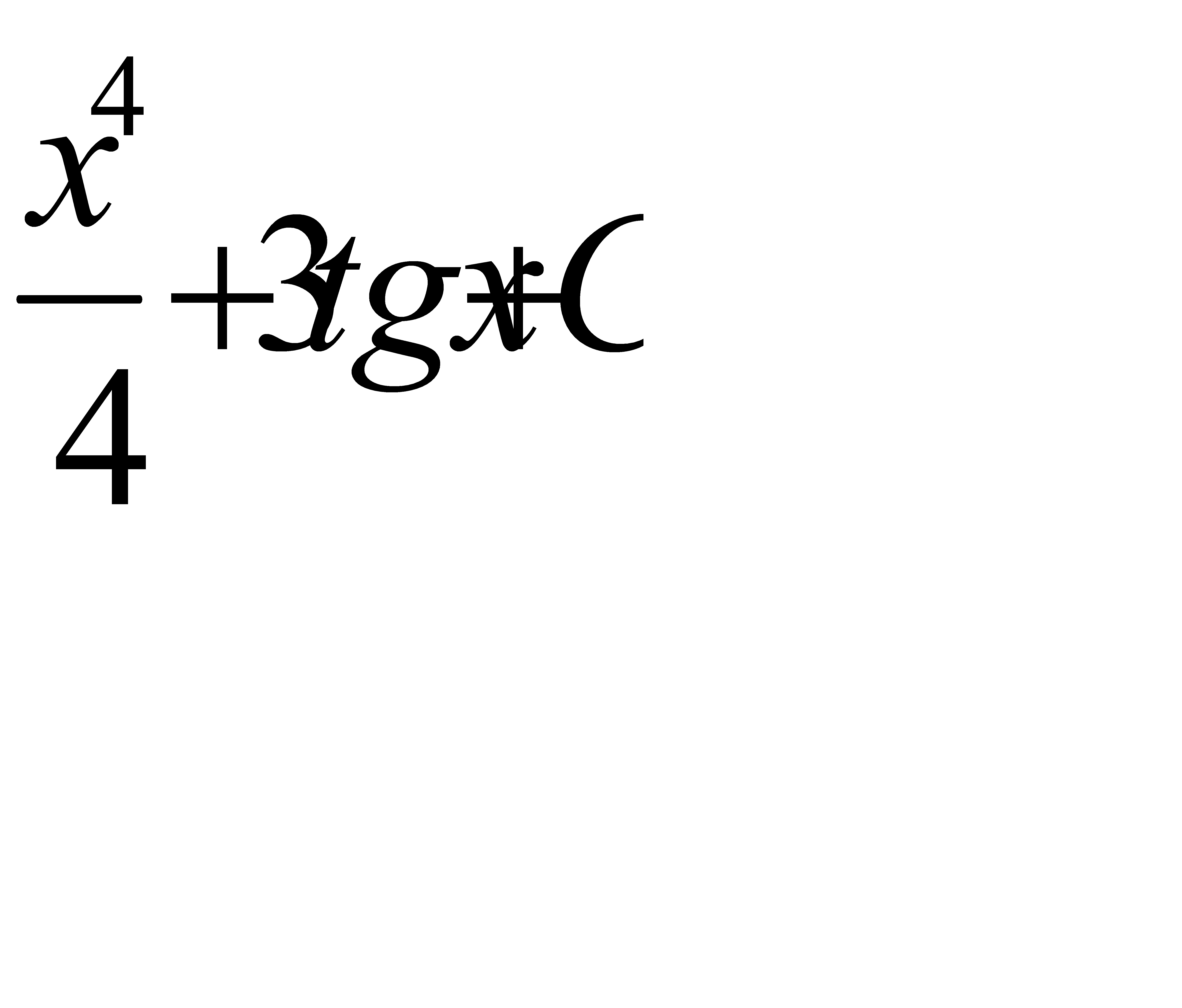 G)
G) 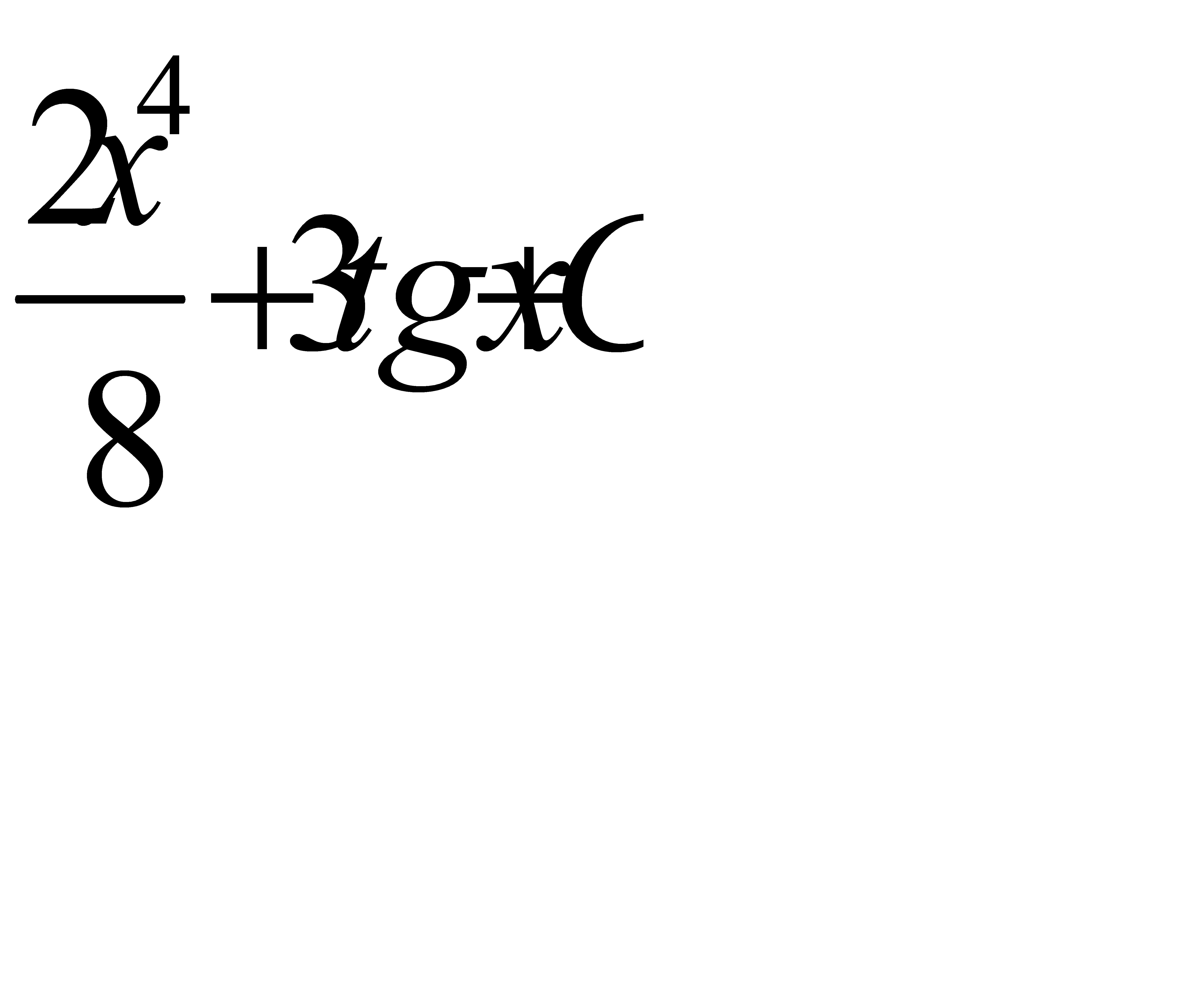 H)
H) 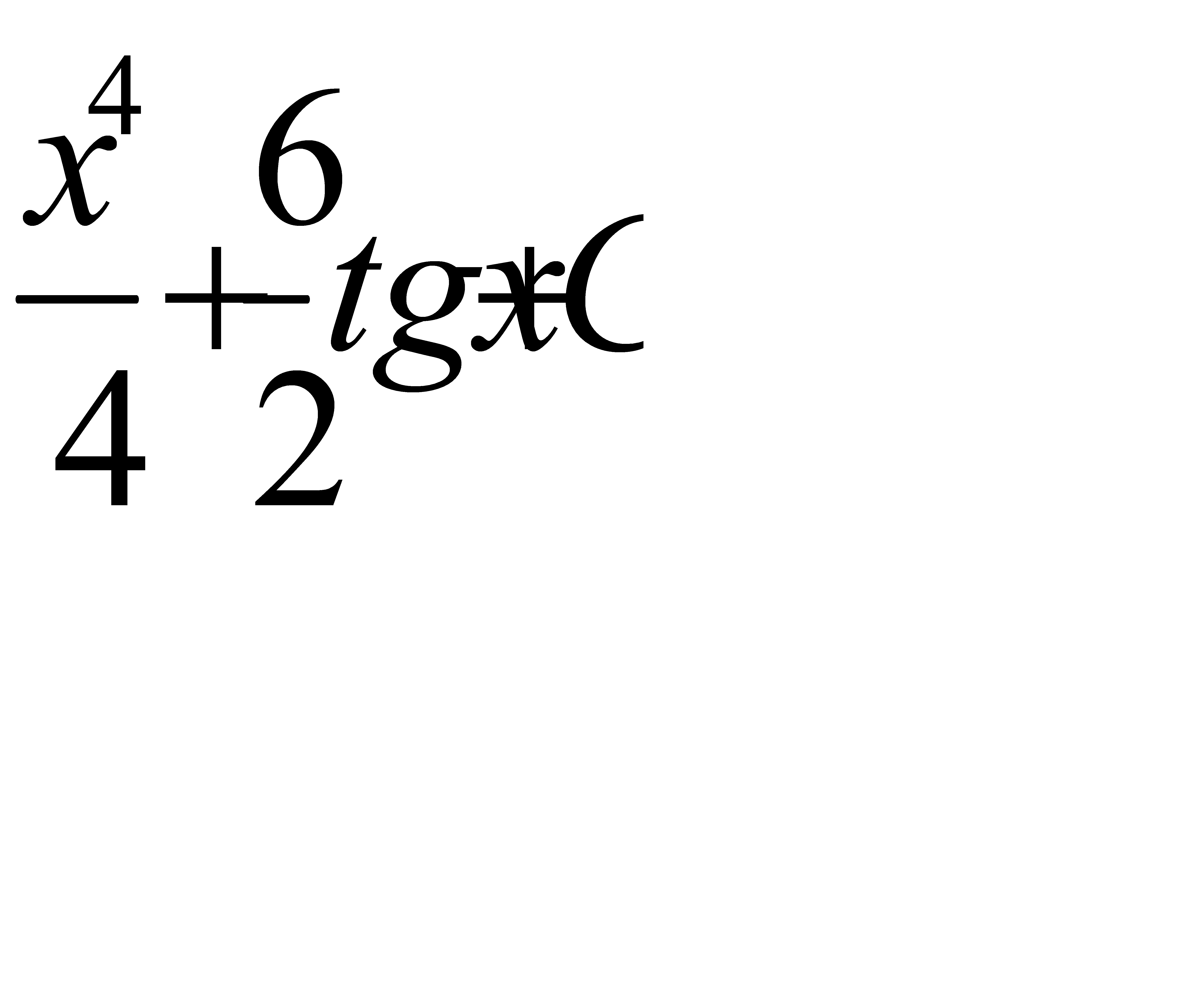
Интегралды есепте: 
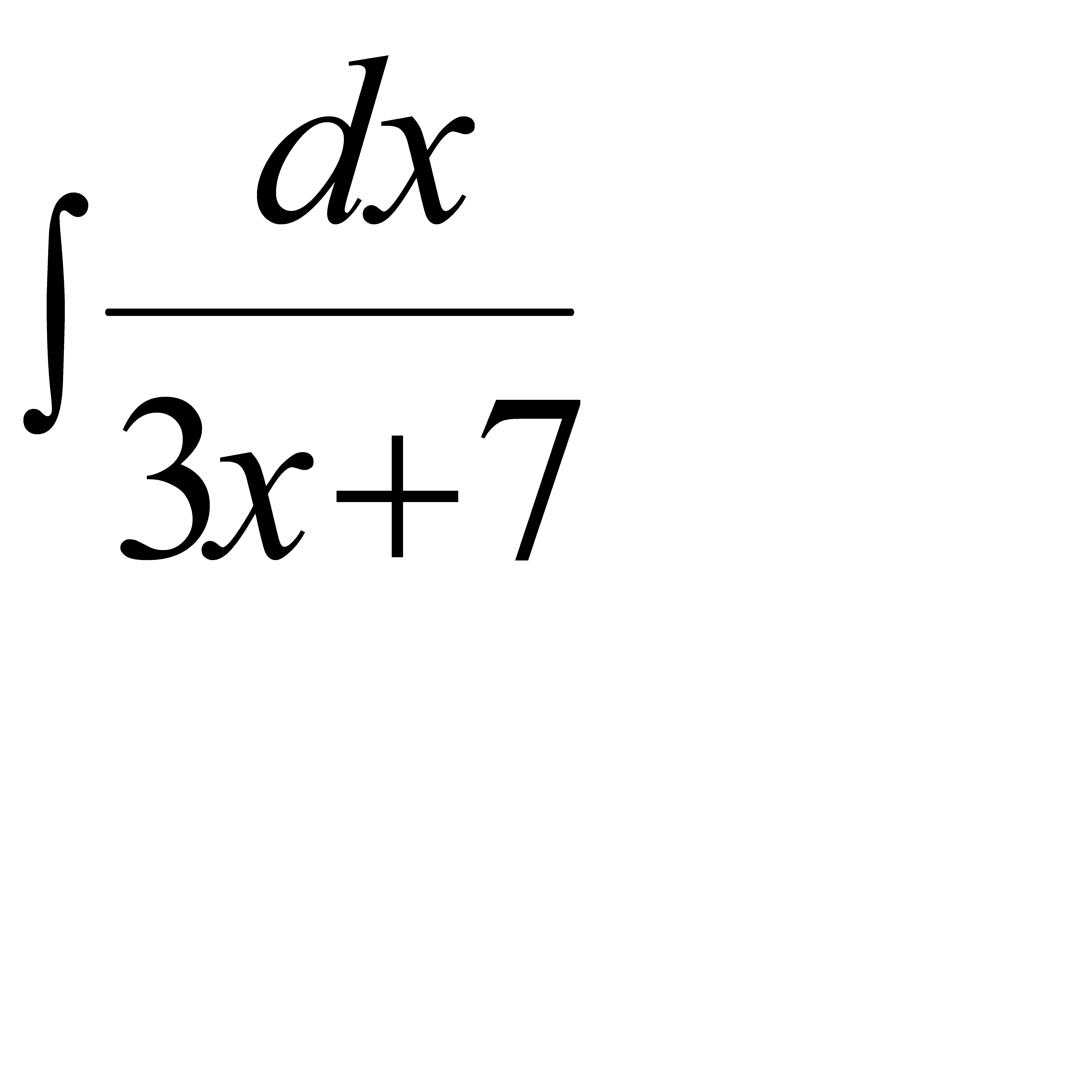 .A)
.A) 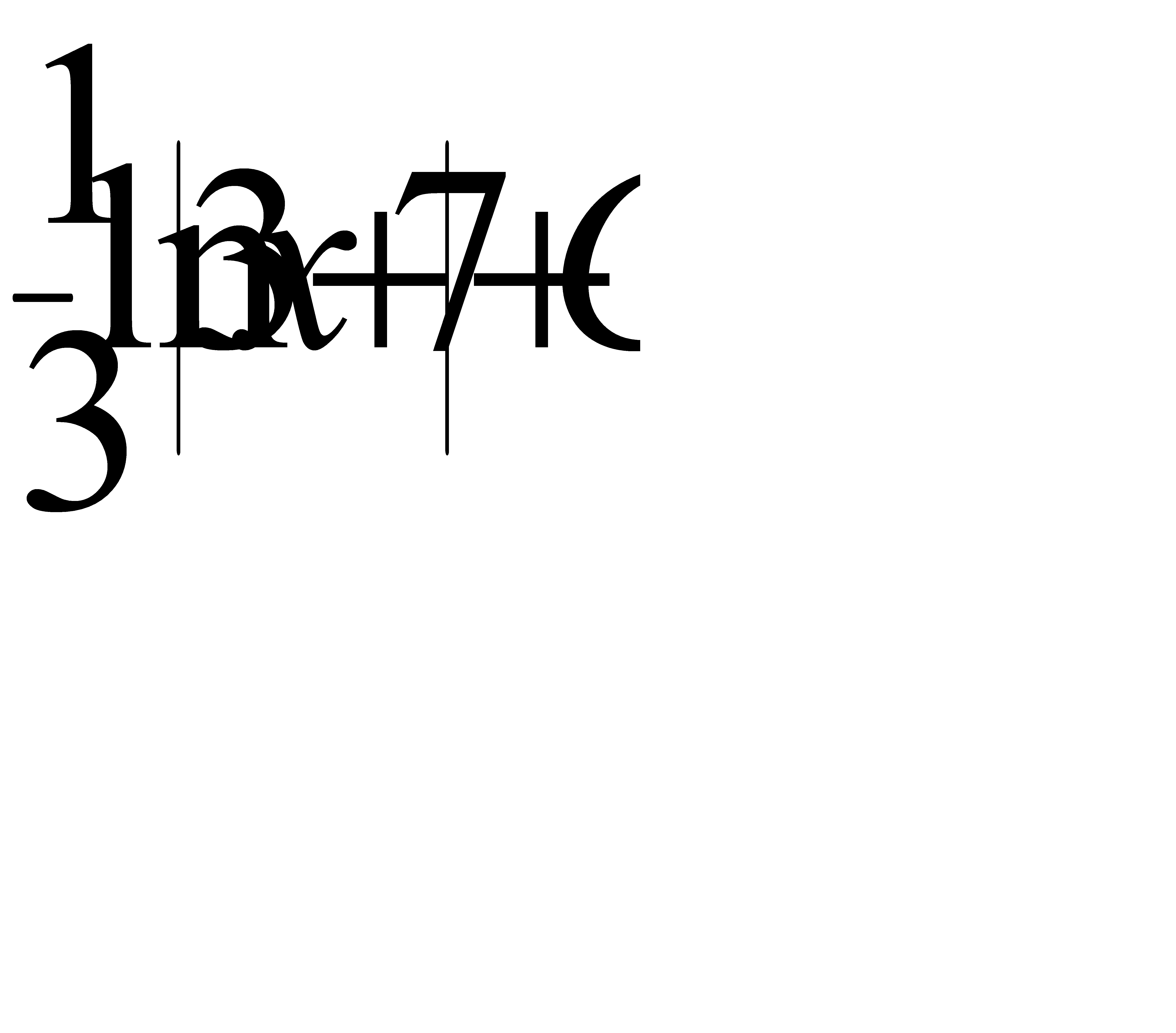 G)
G) 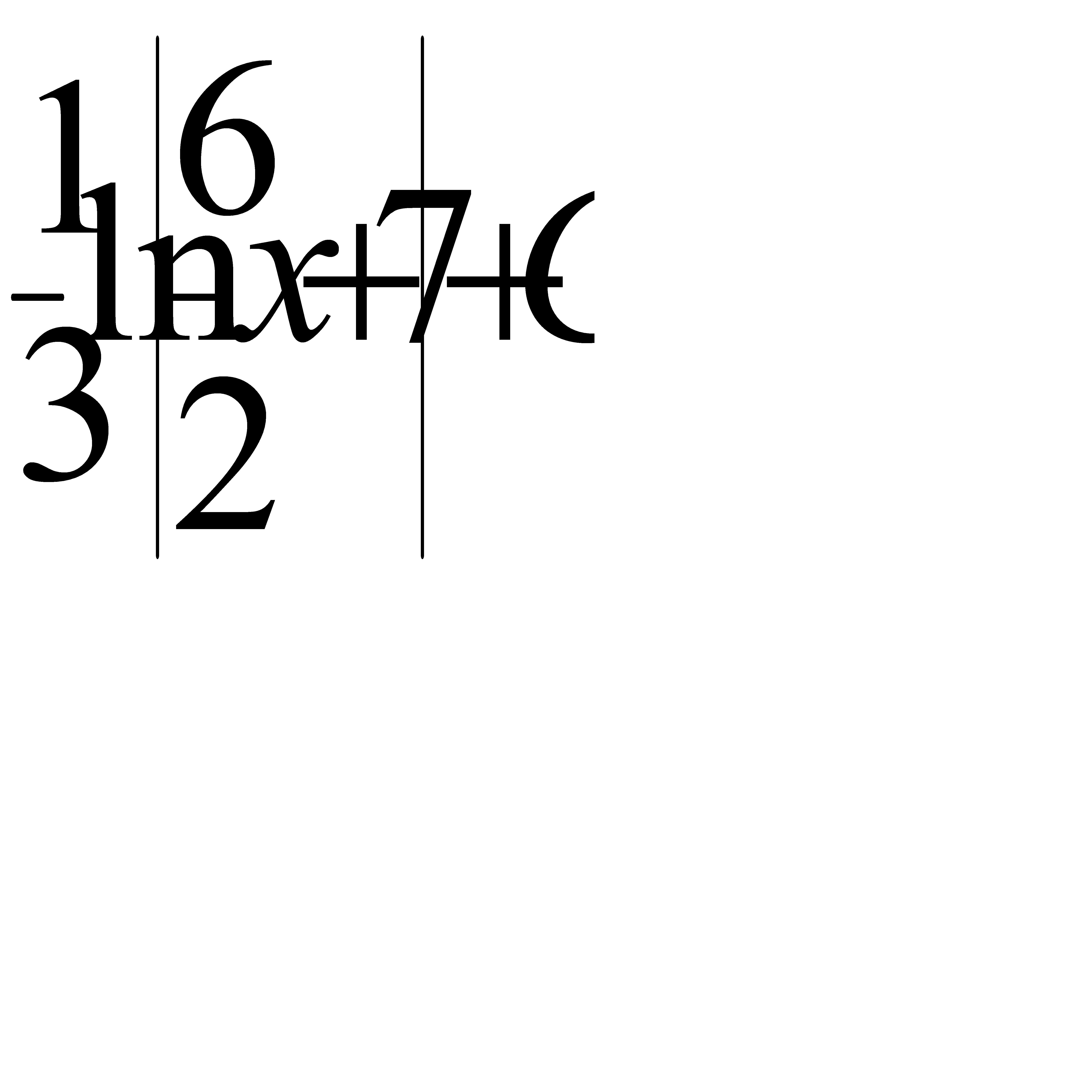 H)
H) 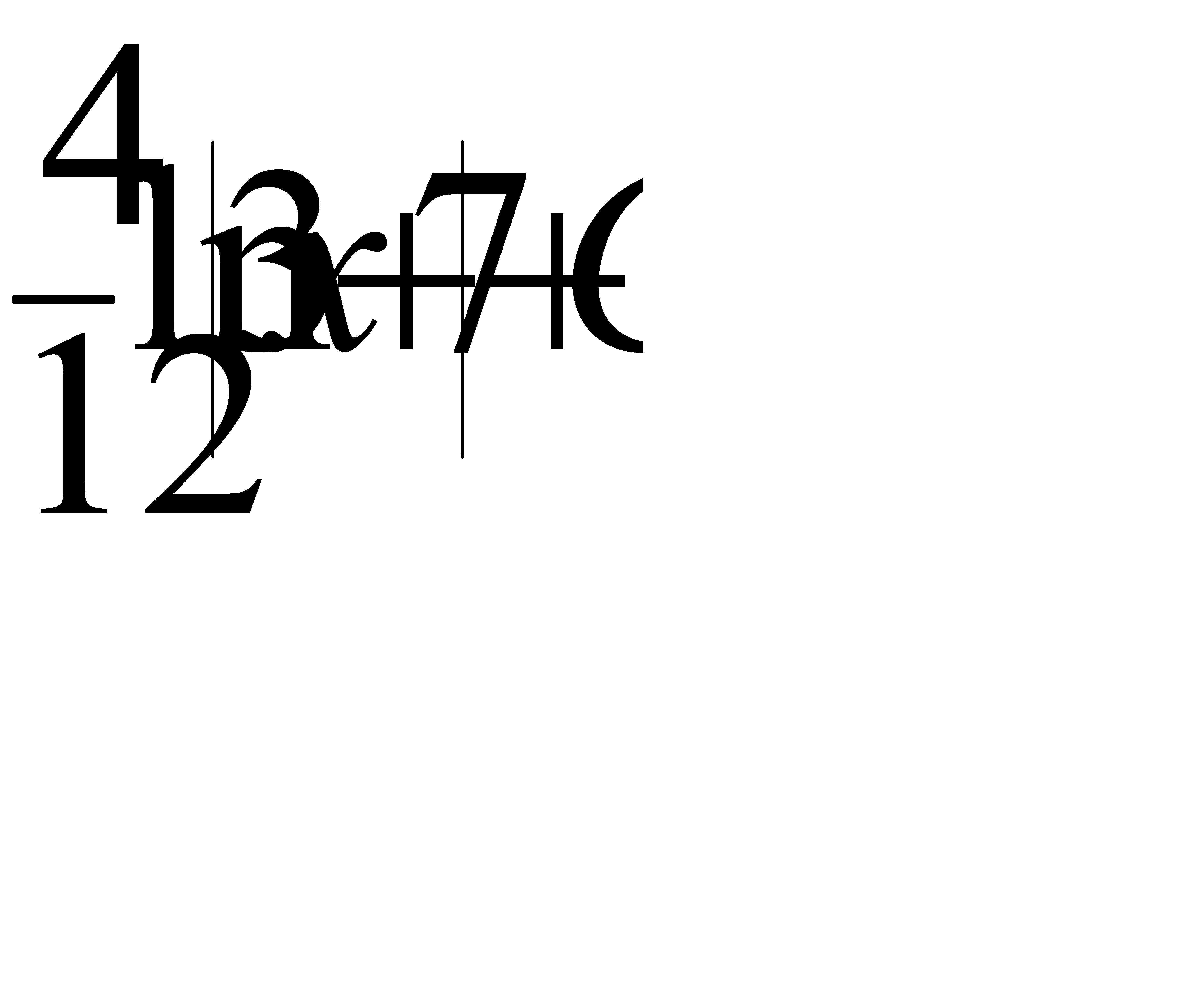
Интегралды есепте:  .A)
.A) 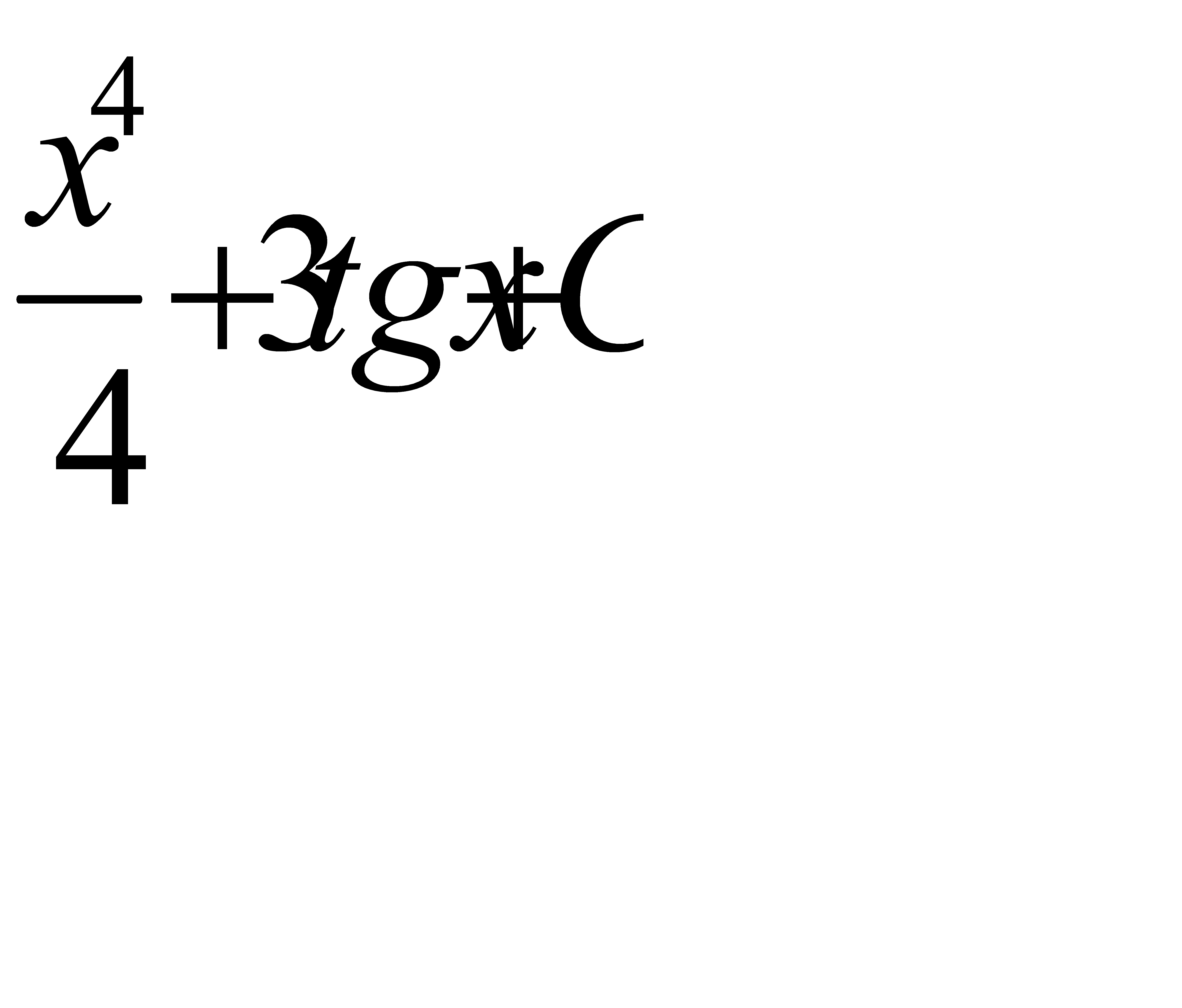 G)
G) 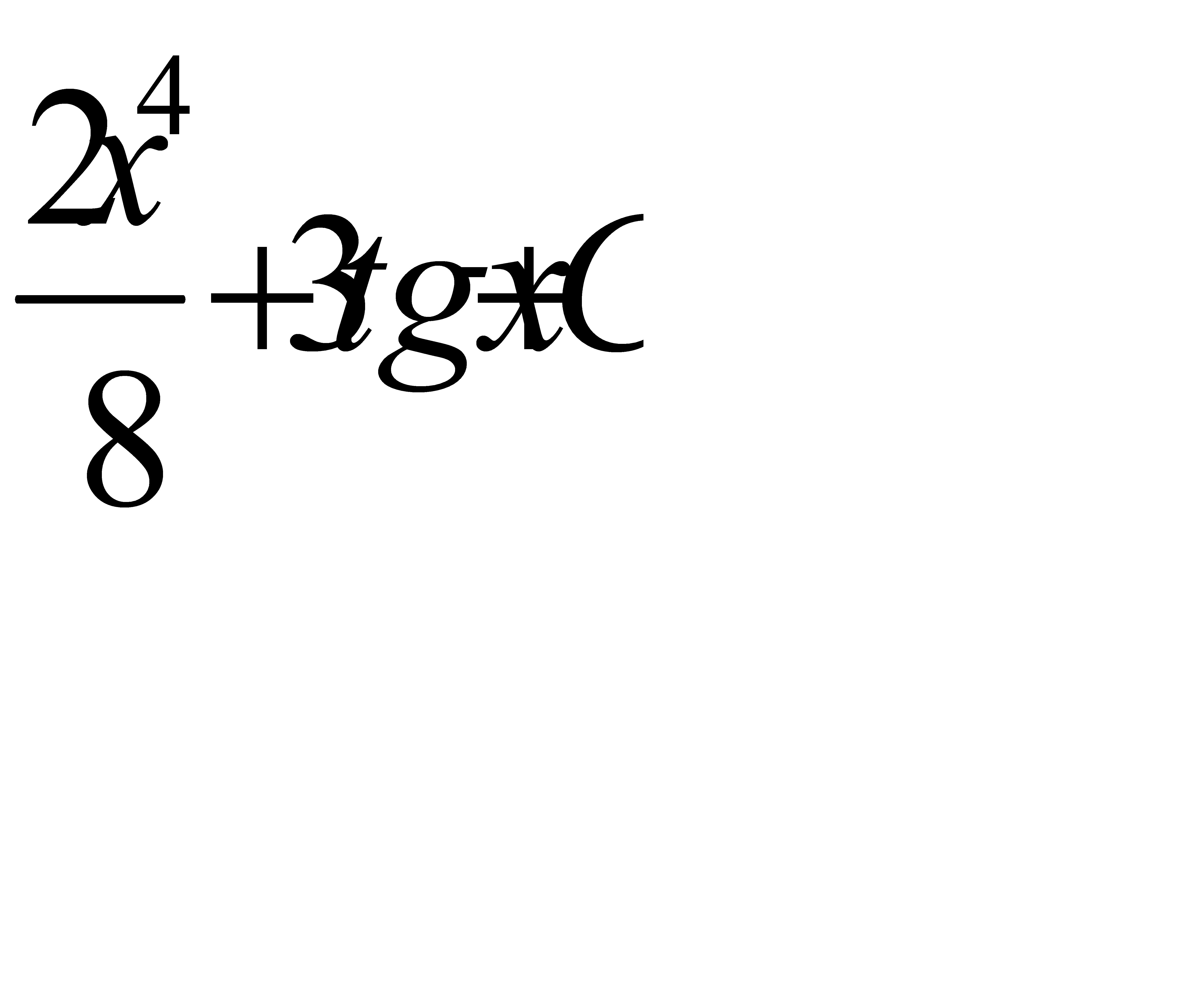 H)
H) 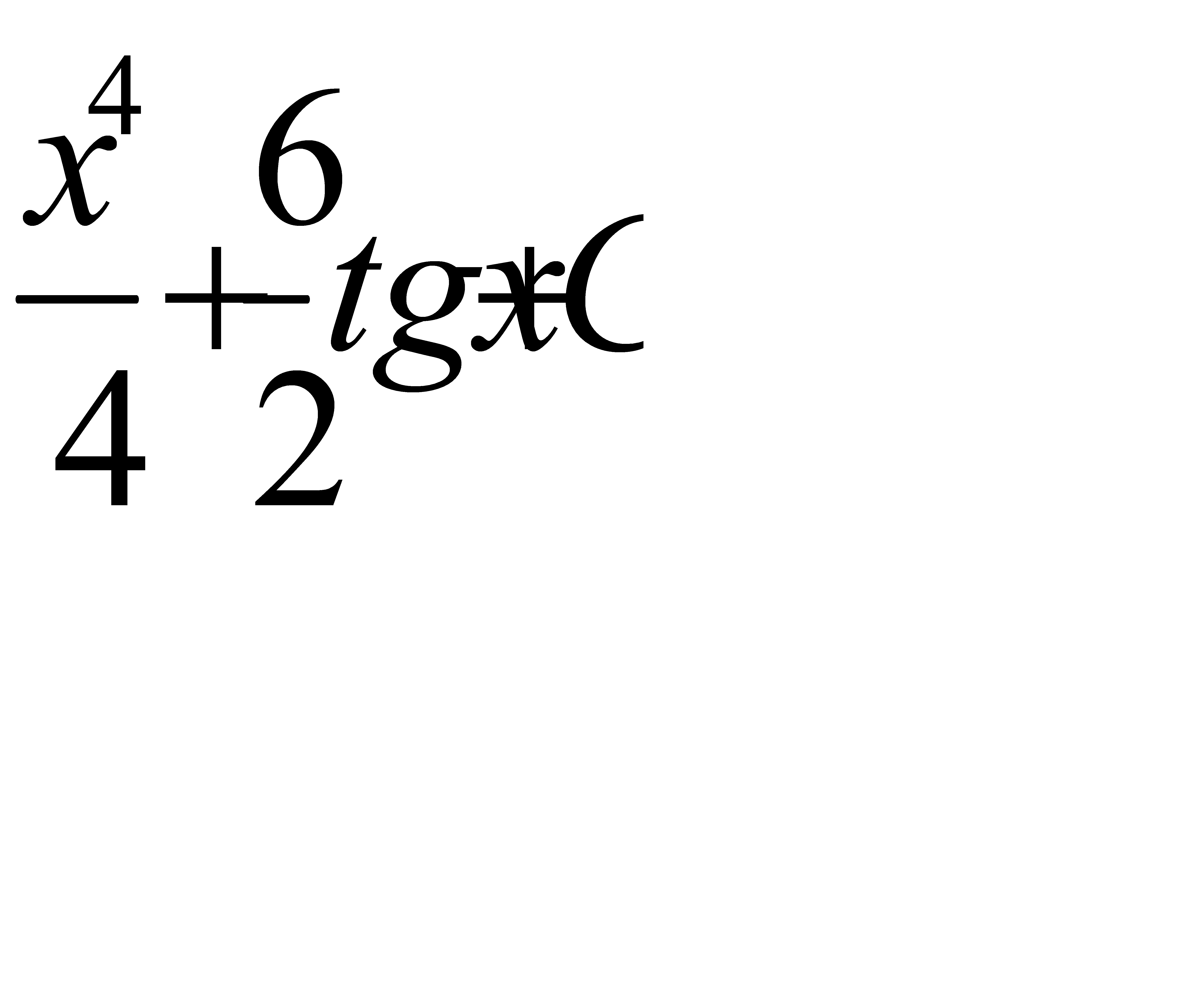
Интегралды есепте: 
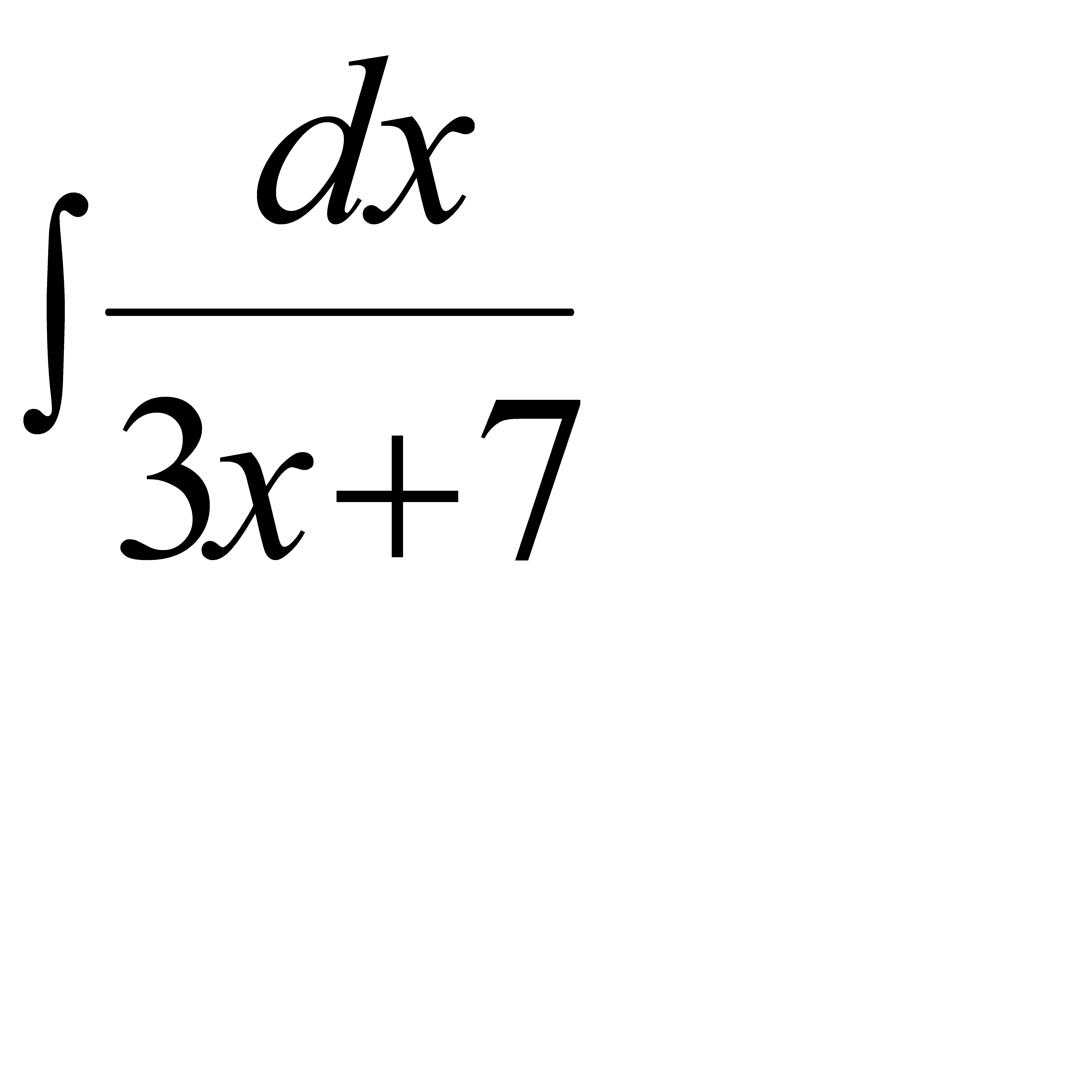 .A)
.A) 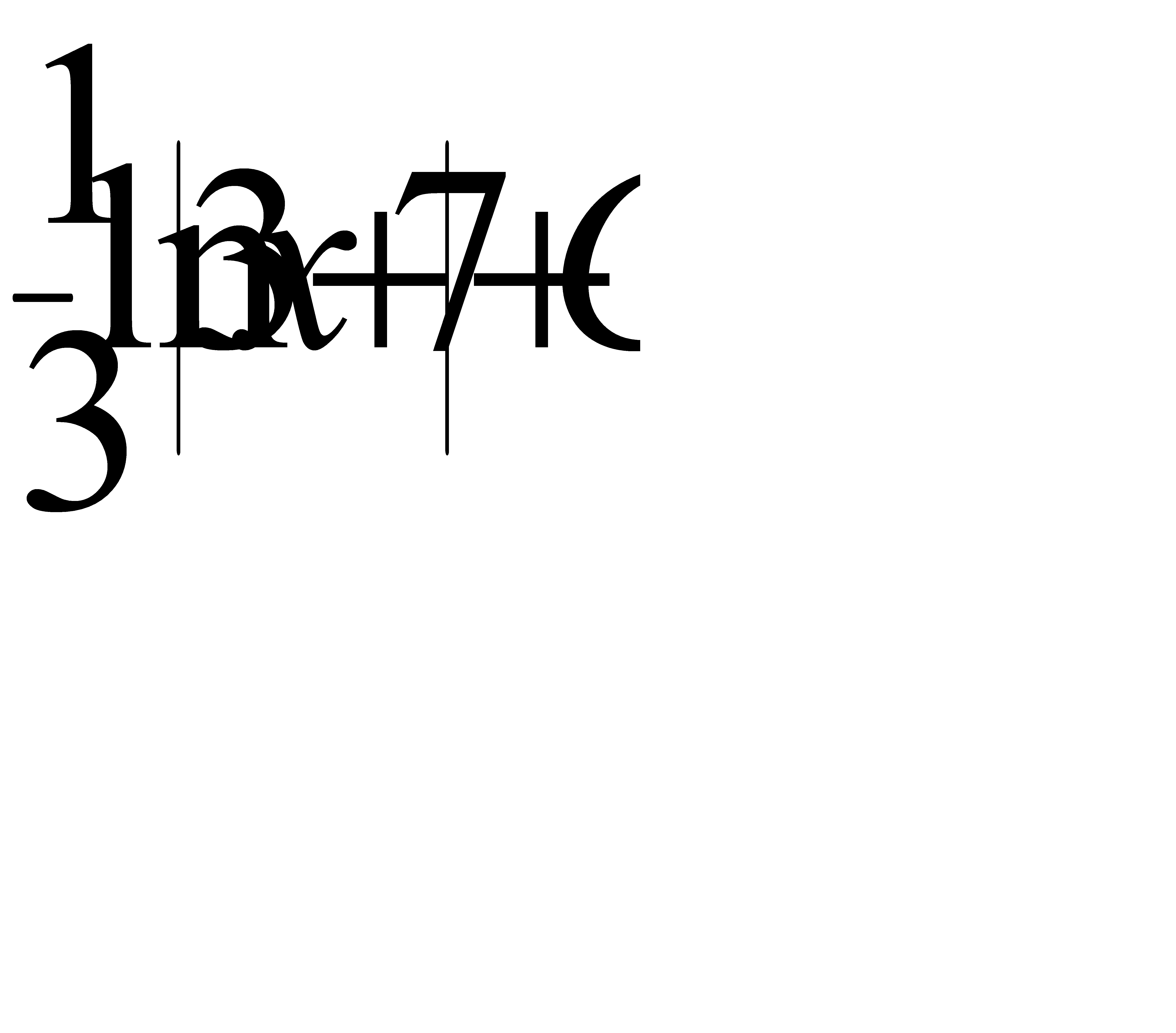 G)
G) 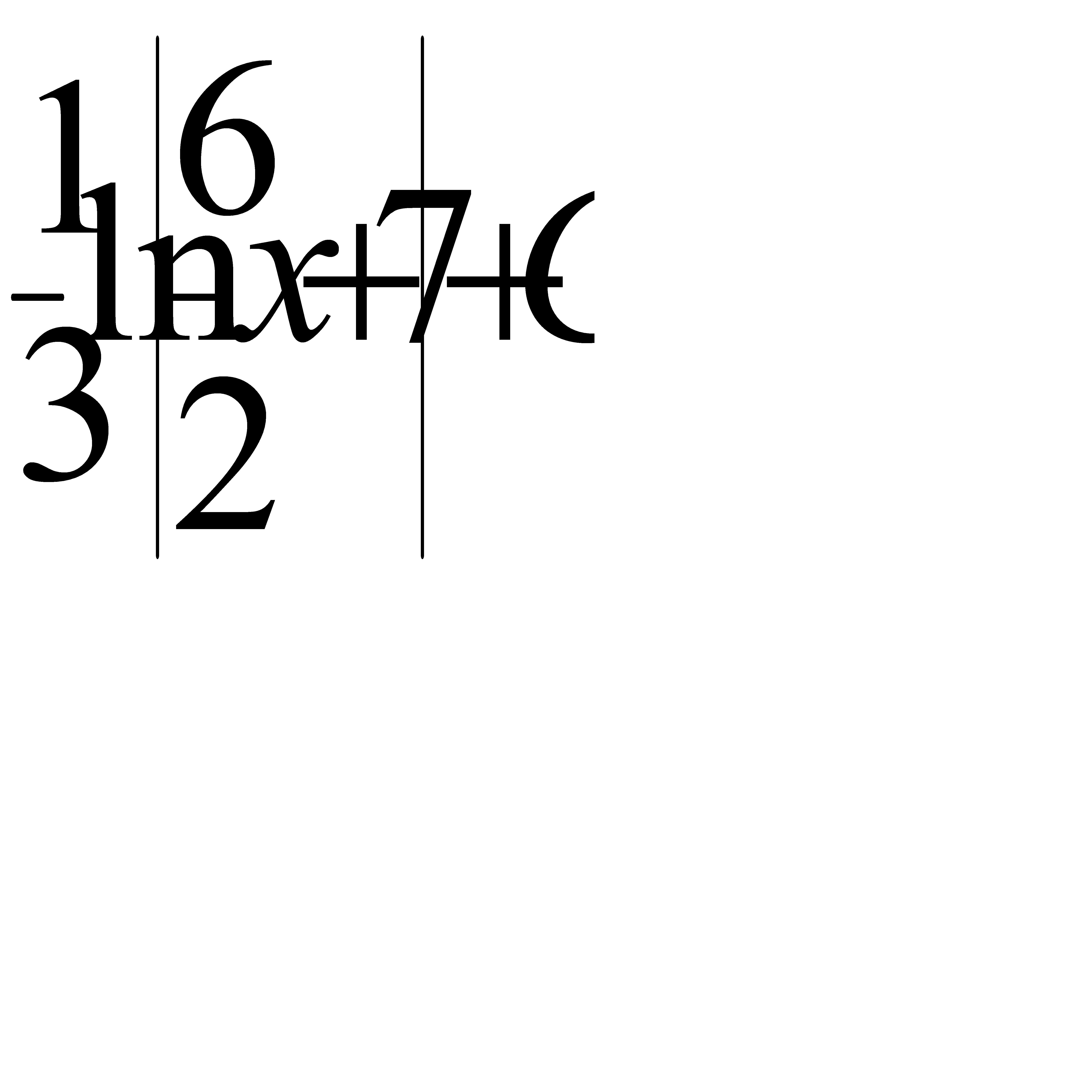 H)
H) 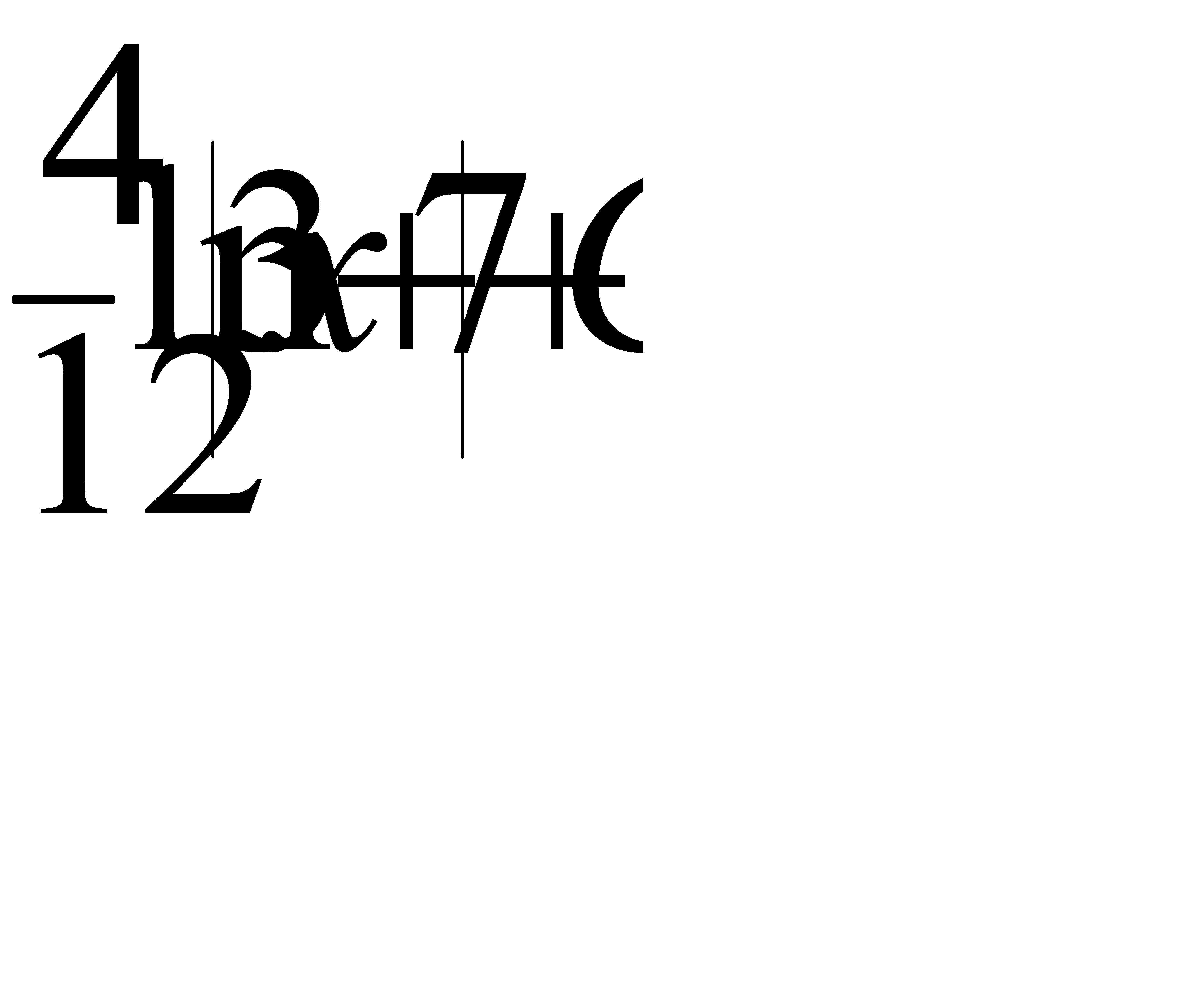
Интегралды есепте: 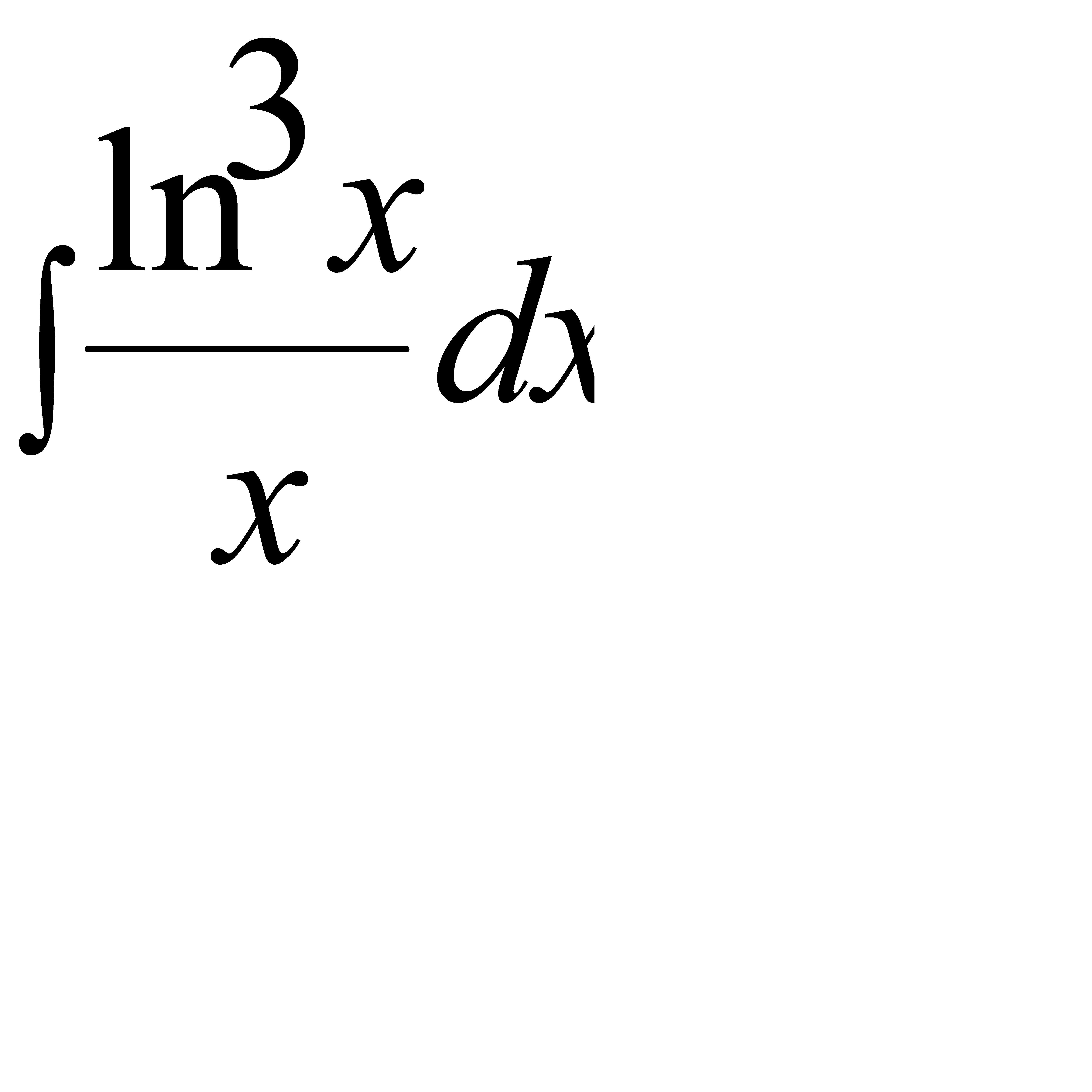 : A)
: A) 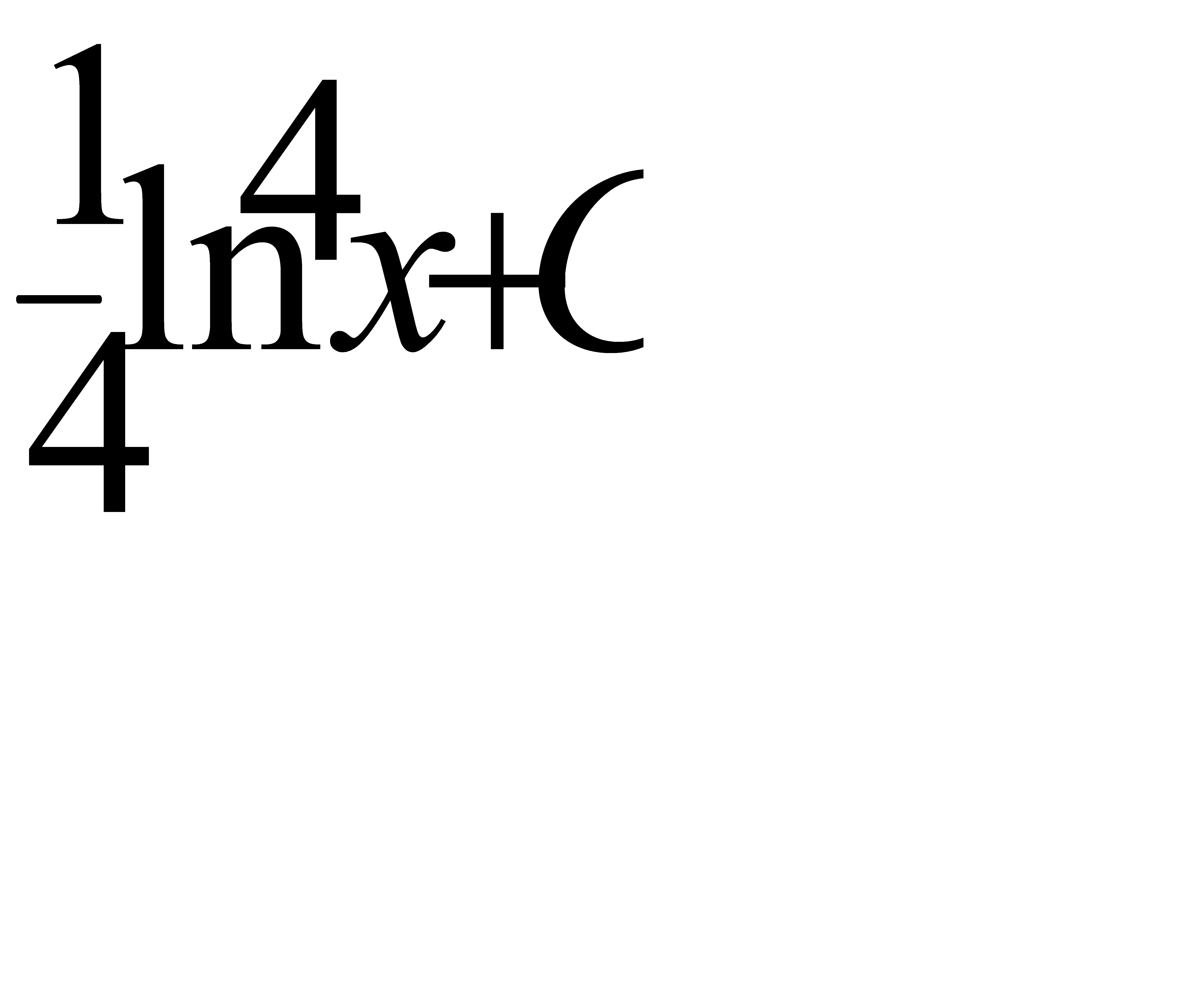 G)
G) 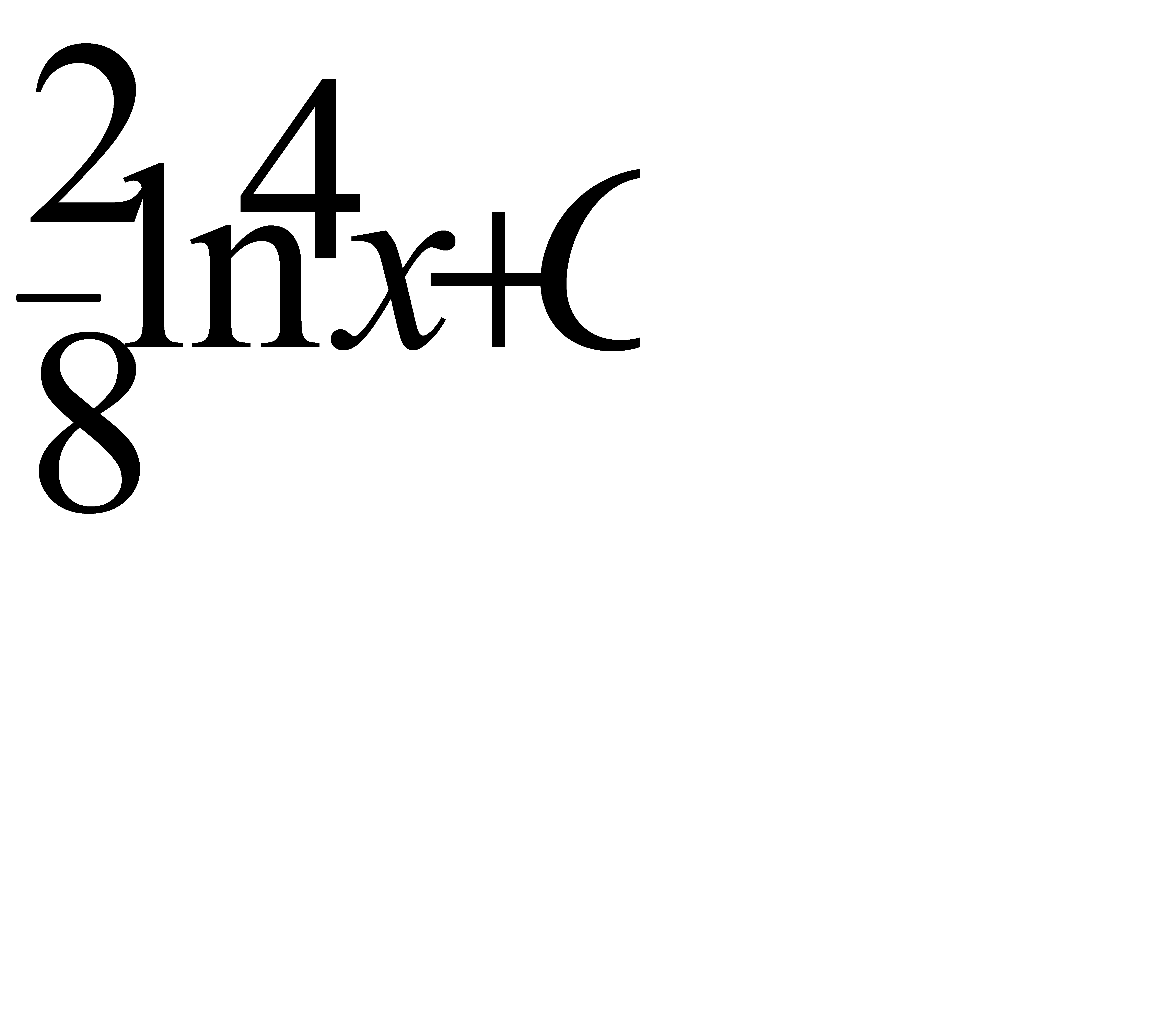 H)
H) 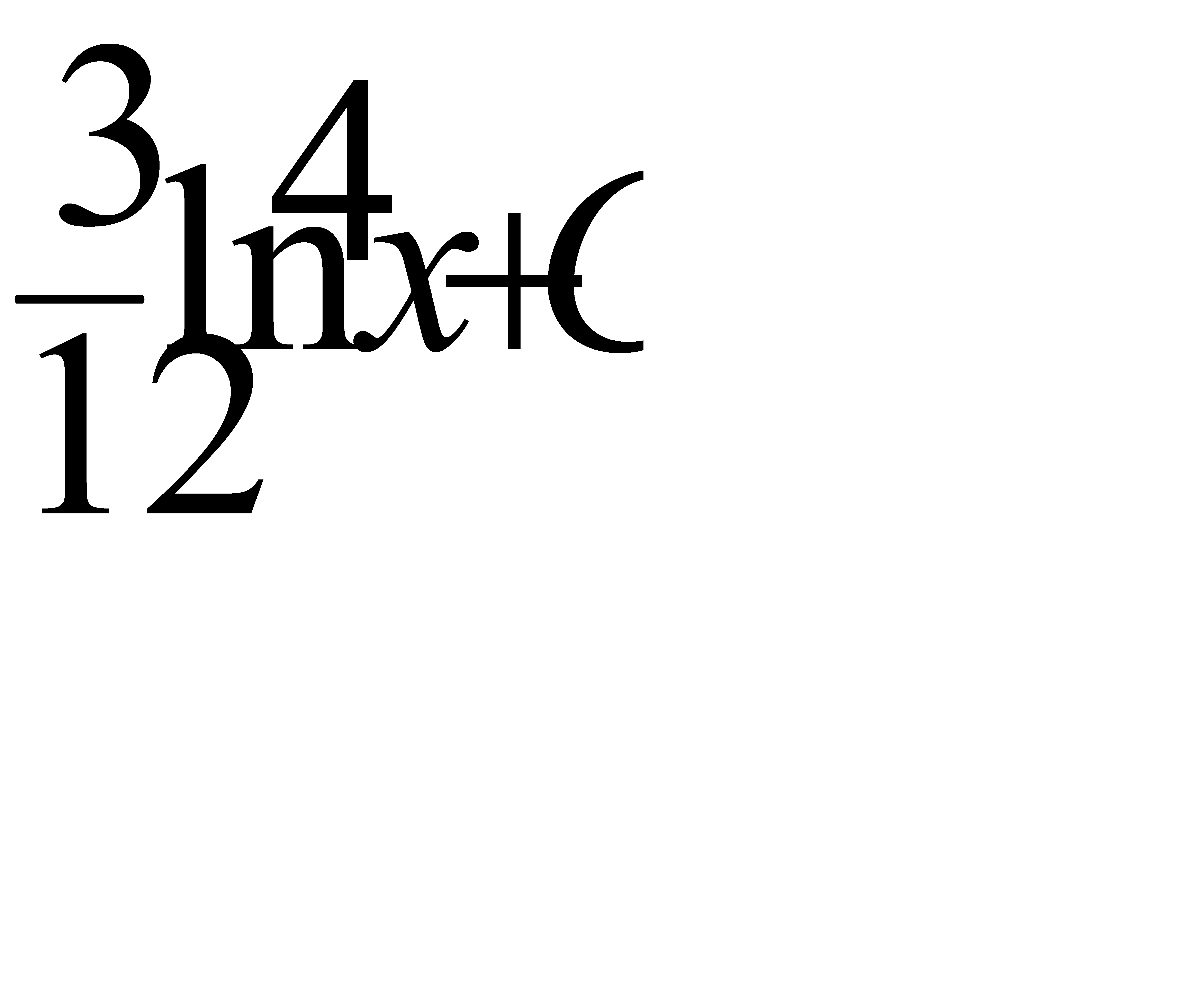
Интегралды есепте: 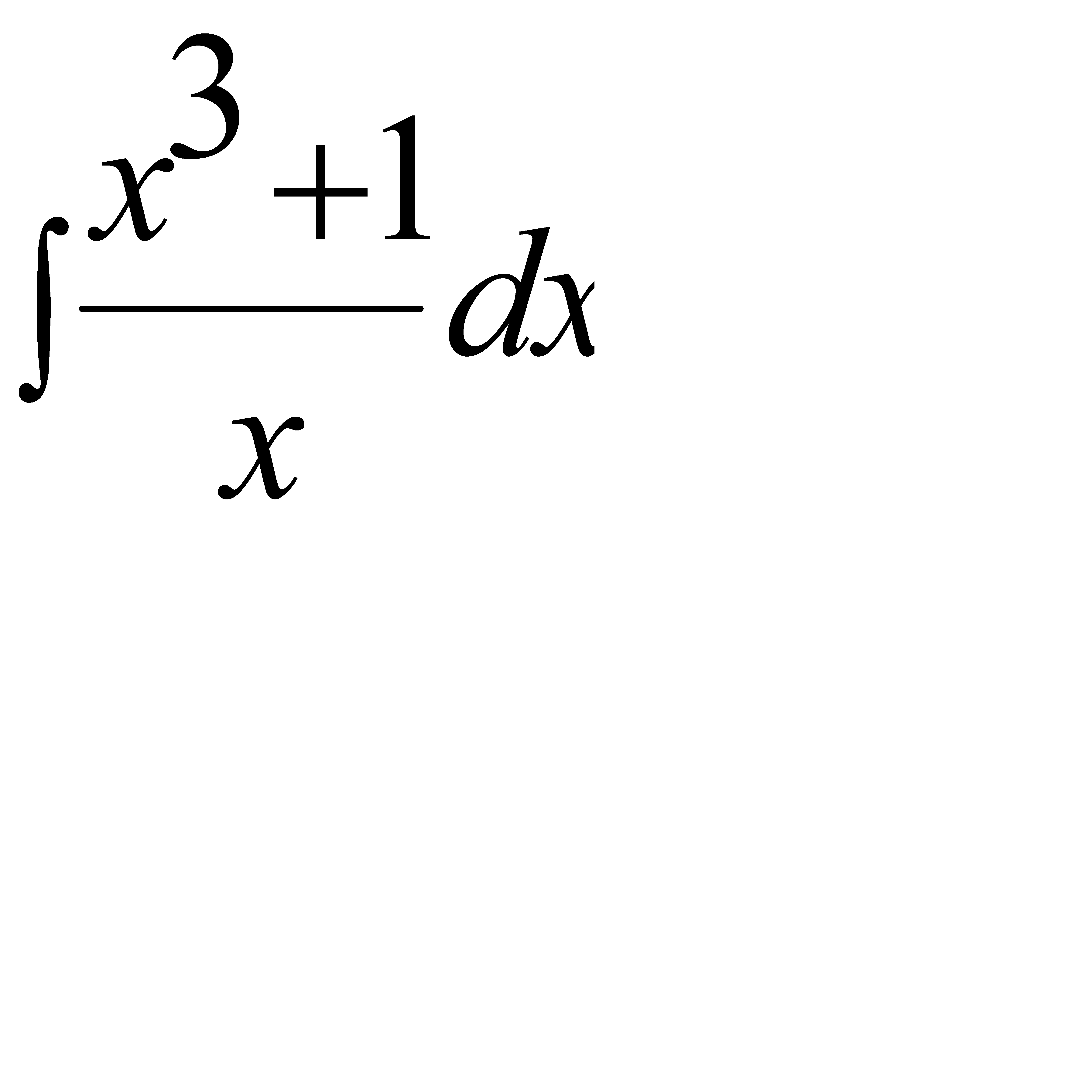 : А) х3/3+lnx+С G) 2х3/6+lnx+С H) 4х3/12+lnx+С
: А) х3/3+lnx+С G) 2х3/6+lnx+С H) 4х3/12+lnx+С
Интегралды есепте: 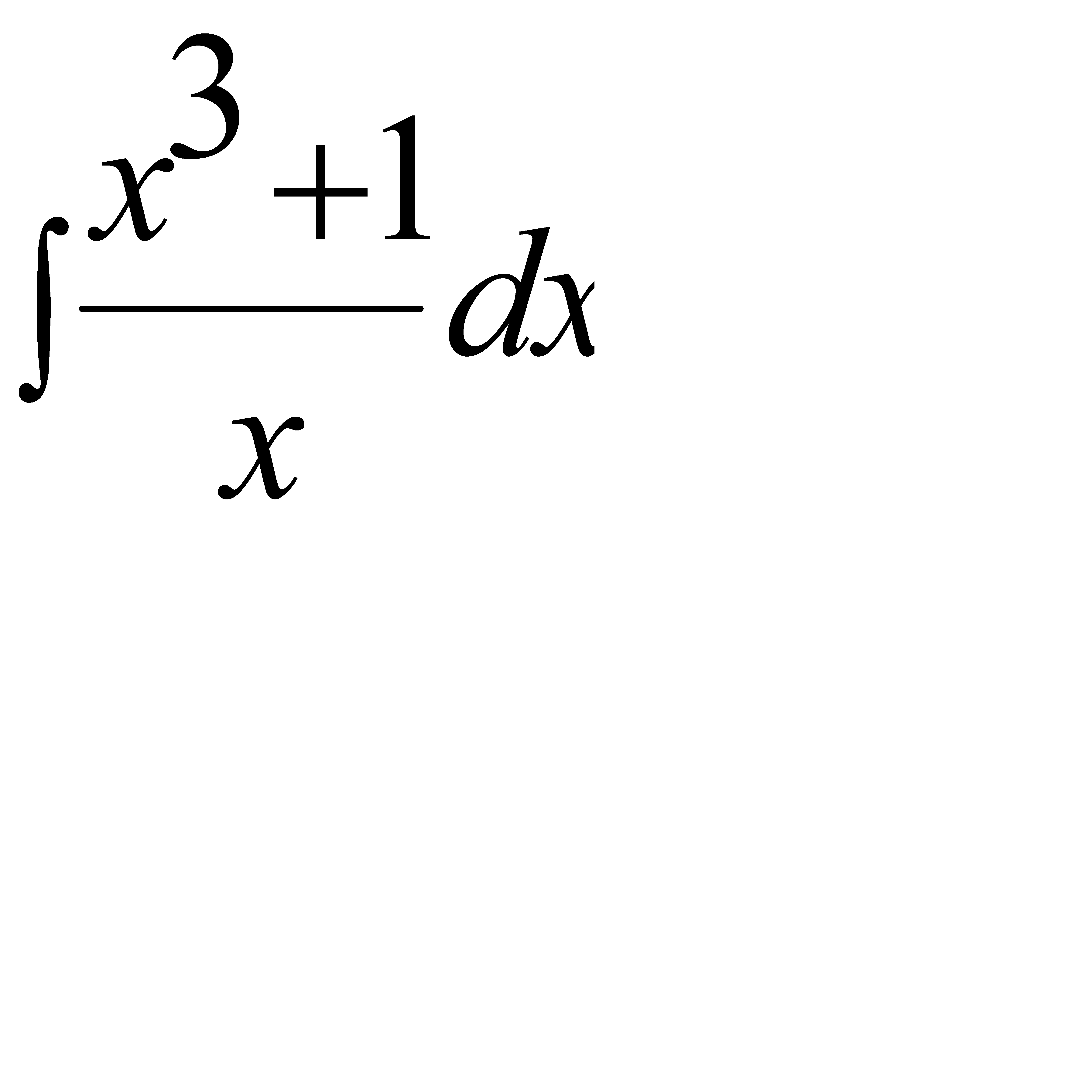 :А) х3/3+lnx+С G) 2х3/6+lnx+С H) 4х3/12+lnx+С
:А) х3/3+lnx+С G) 2х3/6+lnx+С H) 4х3/12+lnx+С
Интегралды табыңыз: 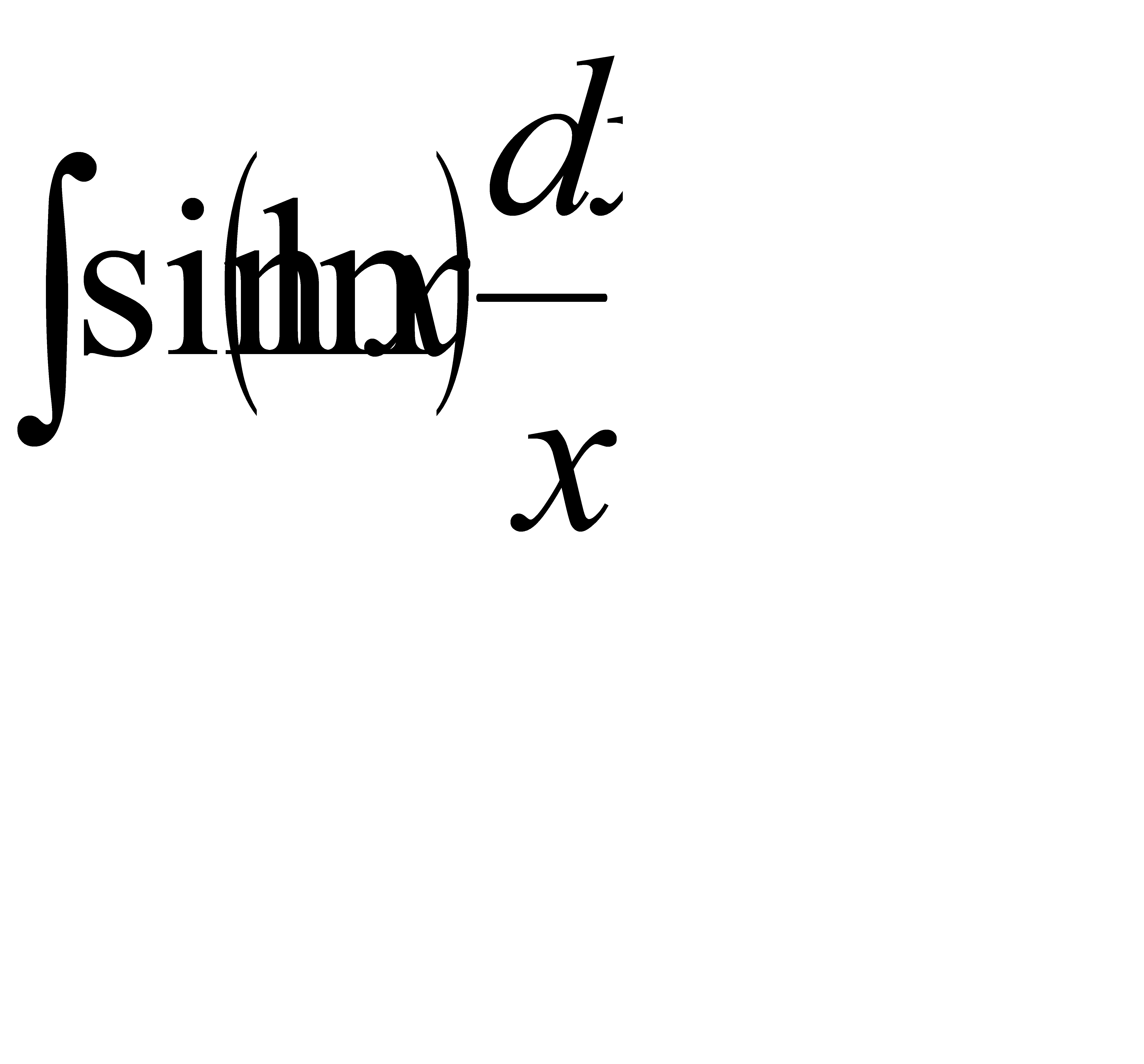 A) -cos(lnx) +C G) 20 cos(lnx) +C H) -30cos(lnx) +C
A) -cos(lnx) +C G) 20 cos(lnx) +C H) -30cos(lnx) +C
Интегралды табыңыз: 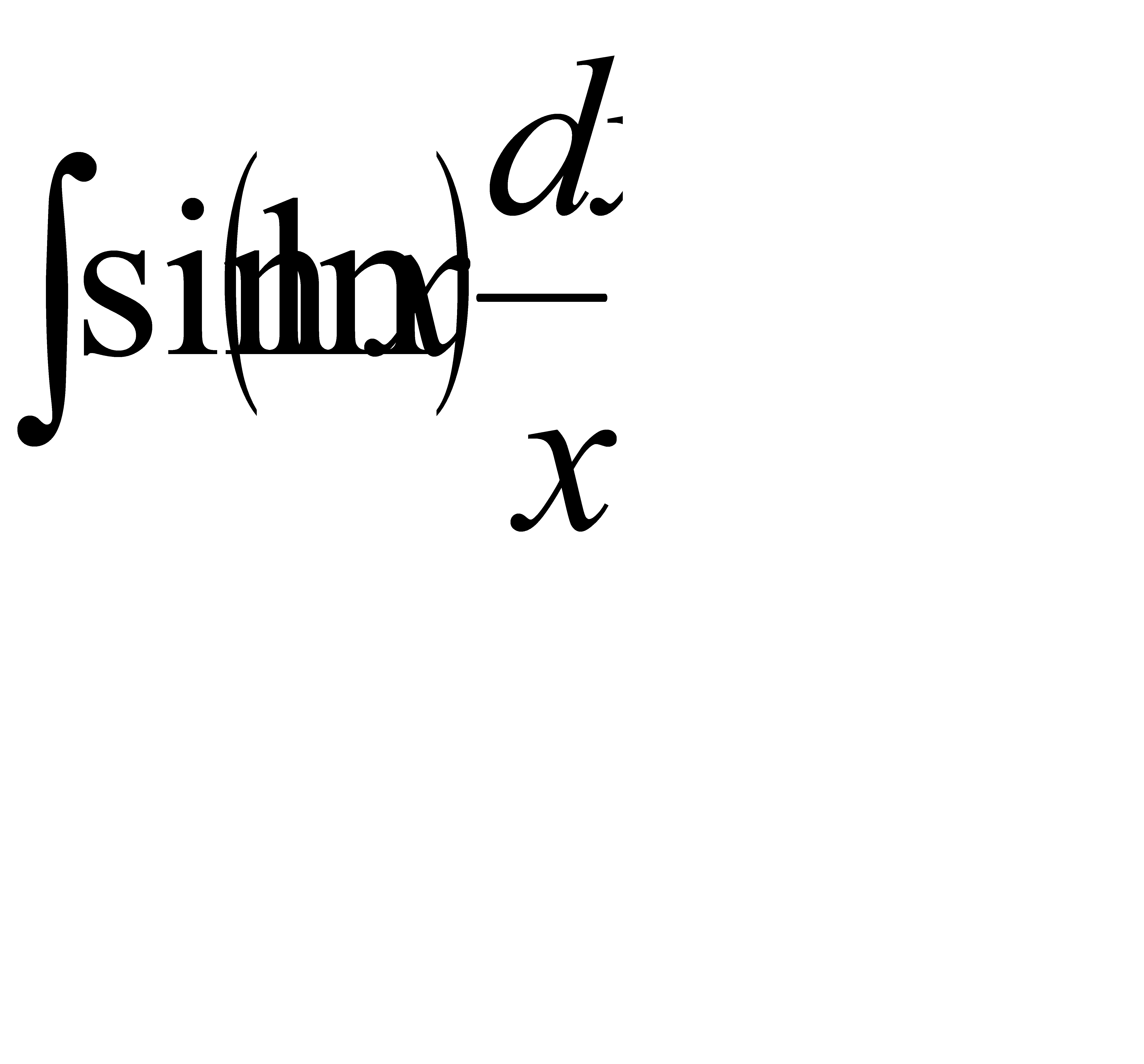 A) -cos(lnx) +C G) 20 cos(lnx) +CH) -30cos(lnx) +C
A) -cos(lnx) +C G) 20 cos(lnx) +CH) -30cos(lnx) +C
Интегралды табыңыз: 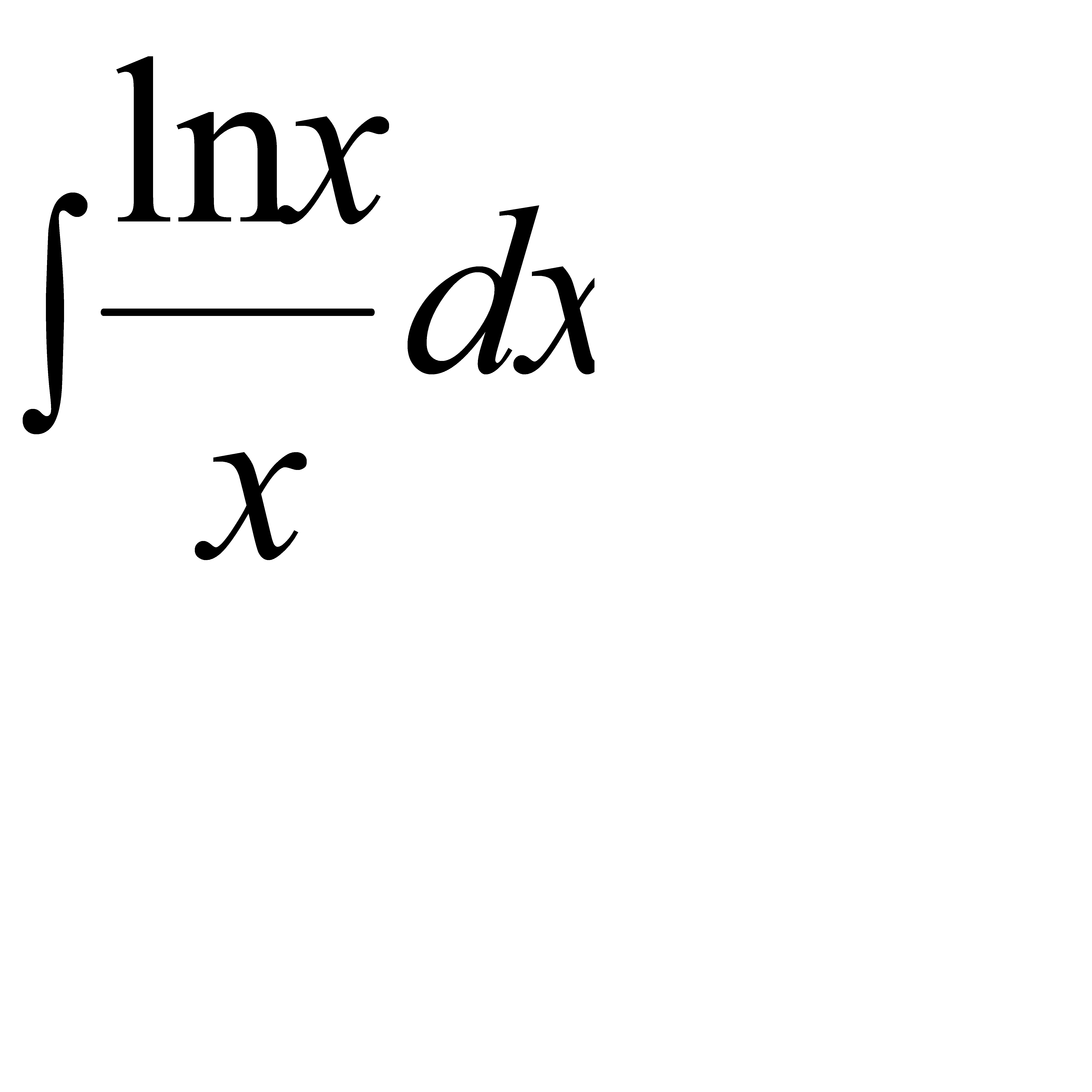 . A)
. A) 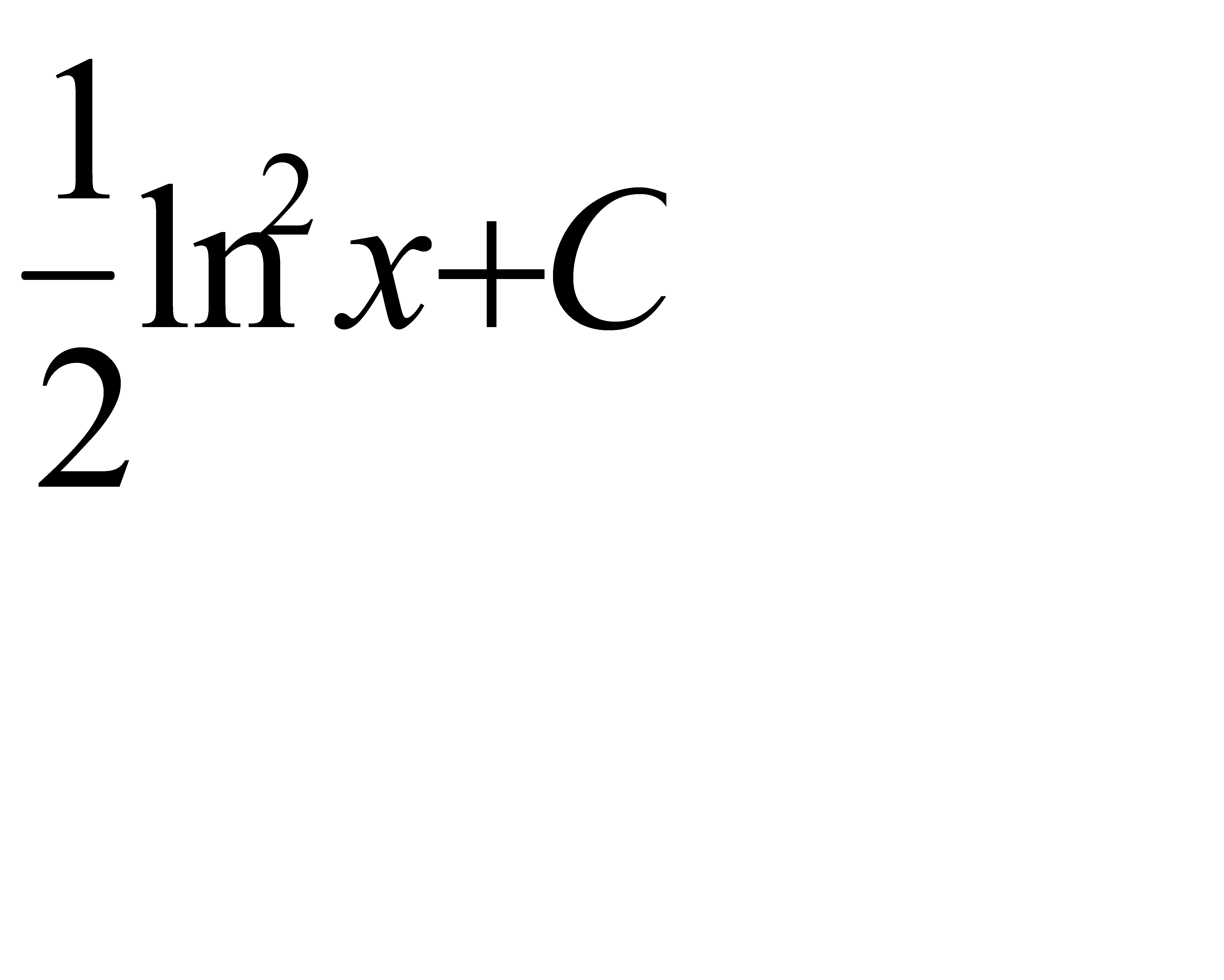 G)
G) 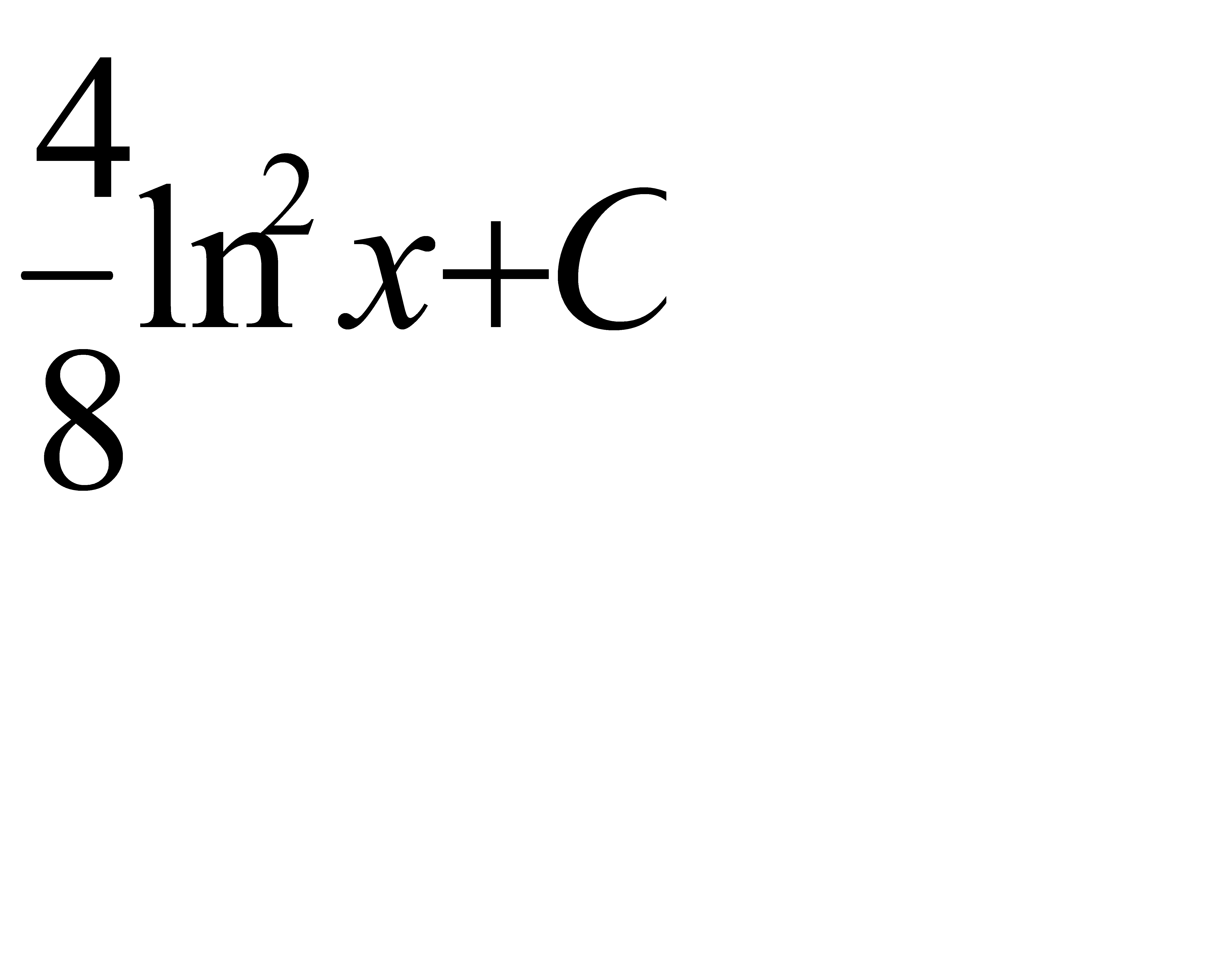 H)
H) 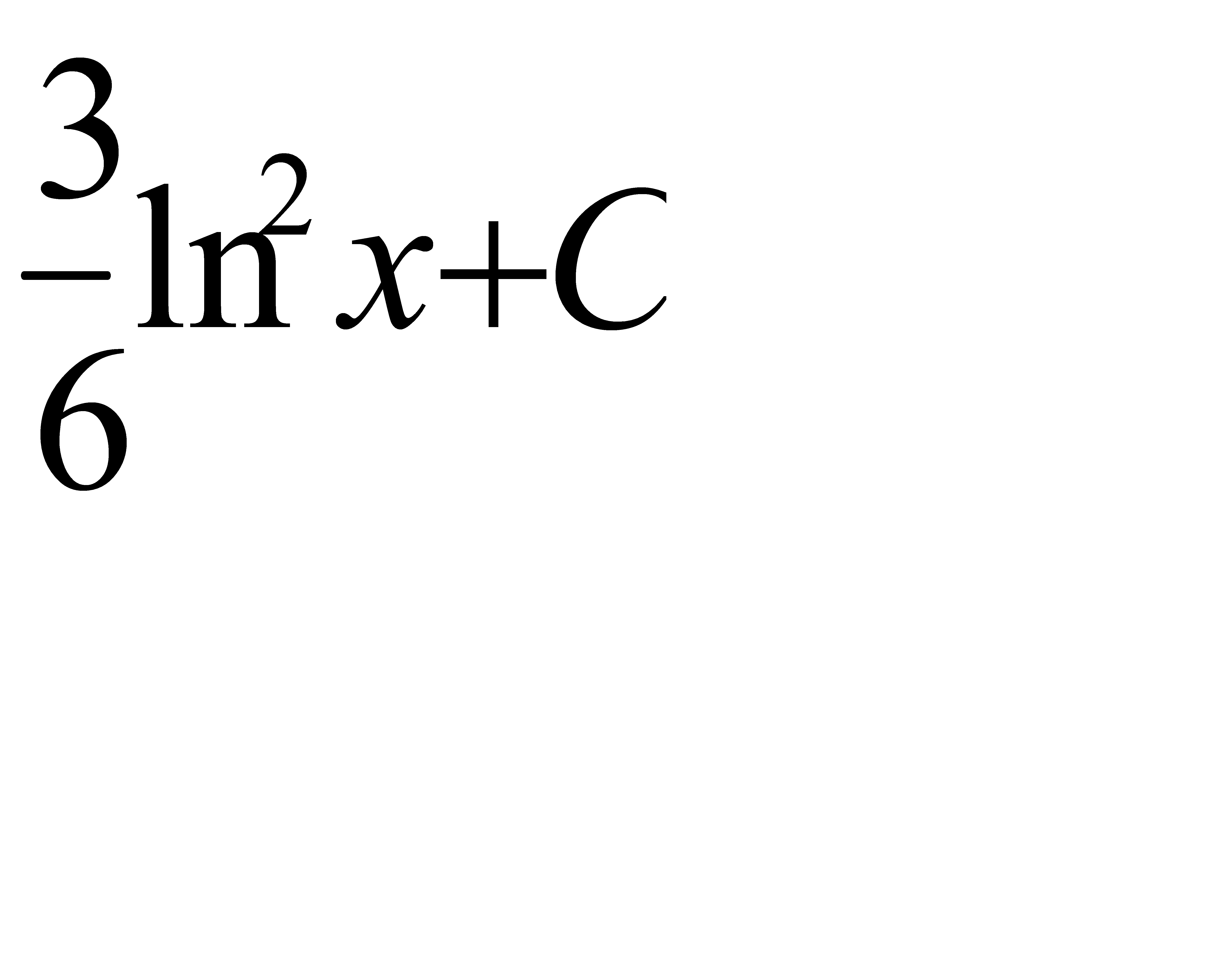
Интегралды табыңыз: 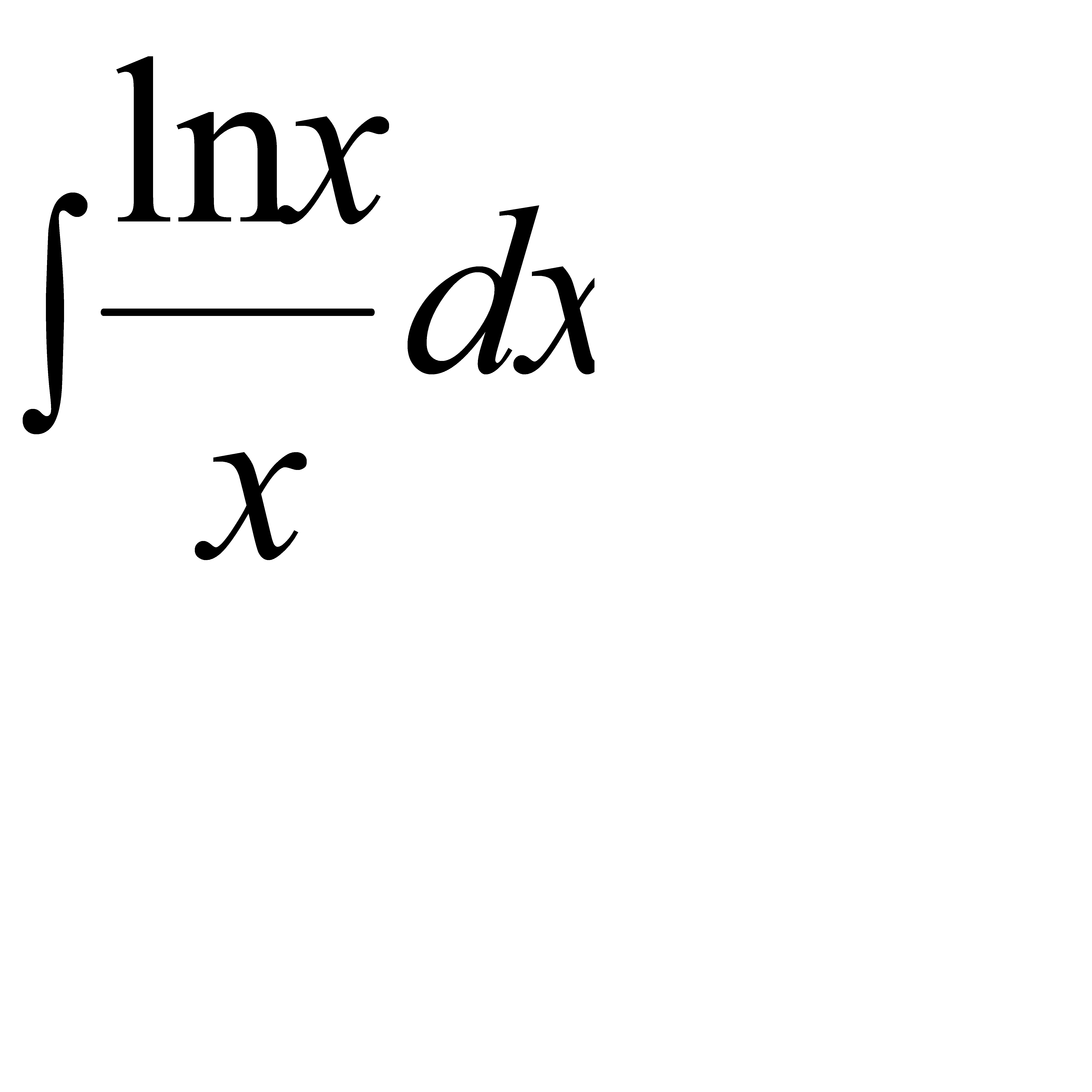 . A)
. A) 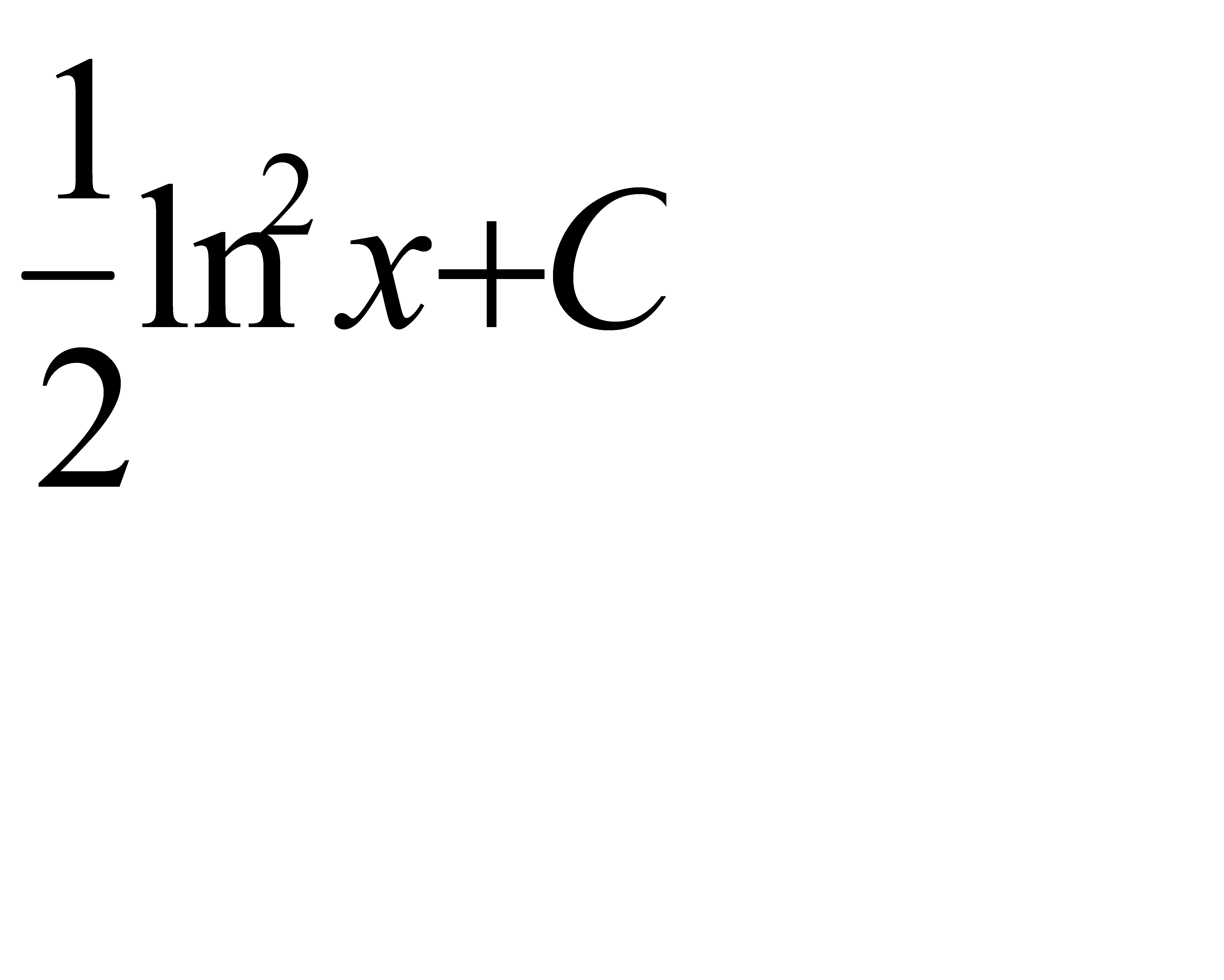 G)
G) 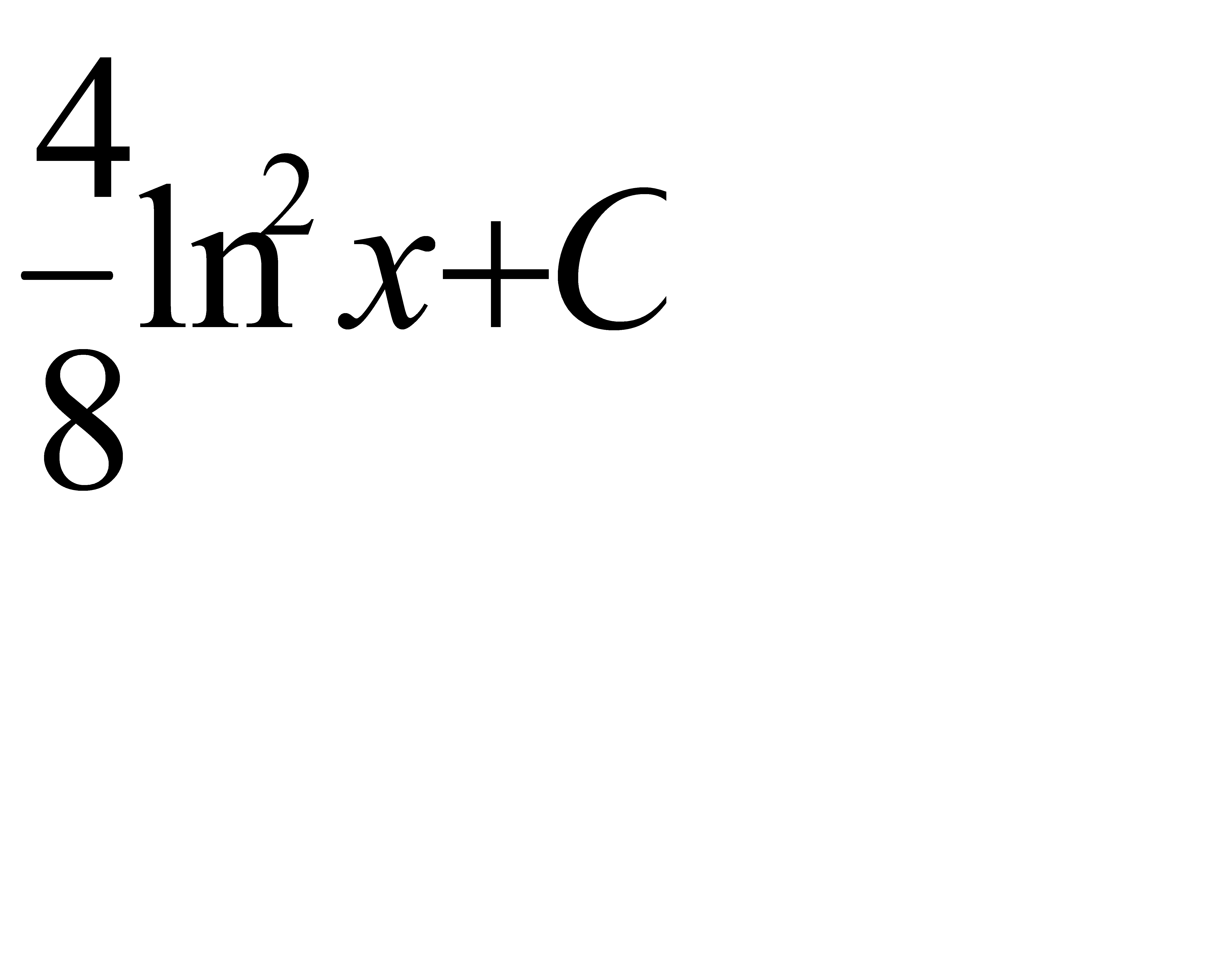 H)
H) 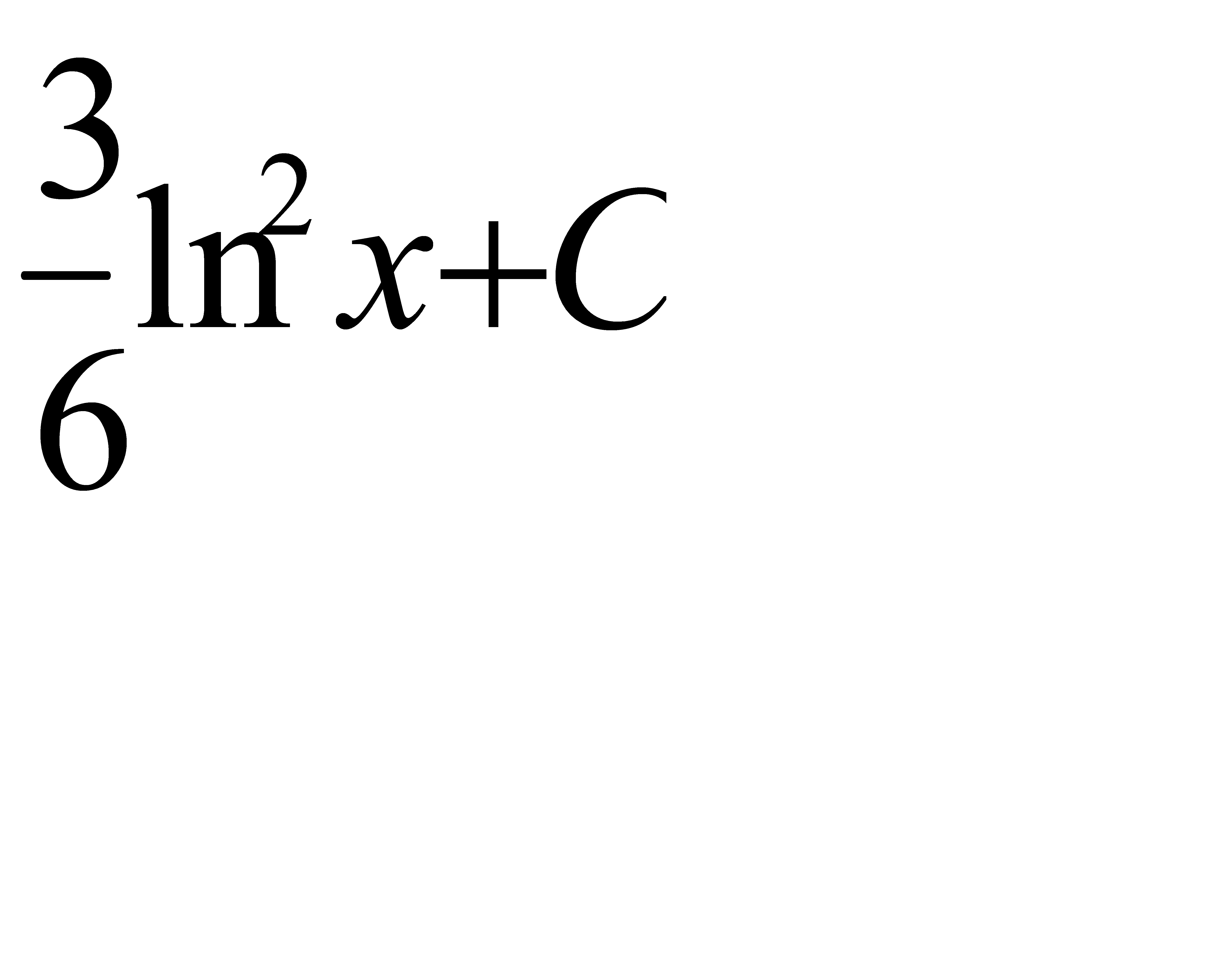
Интегралды табыңыз: 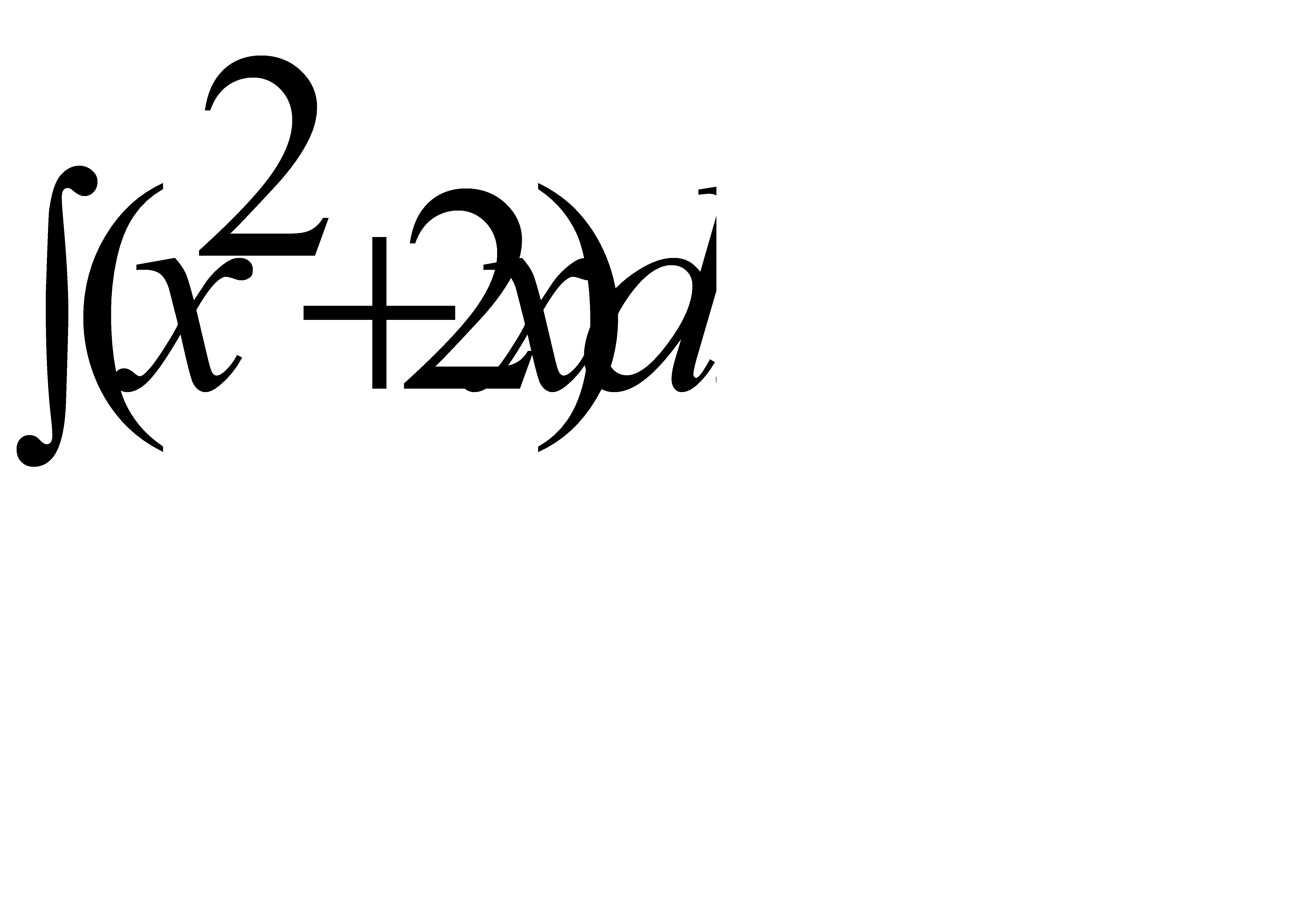 .A)
.A) 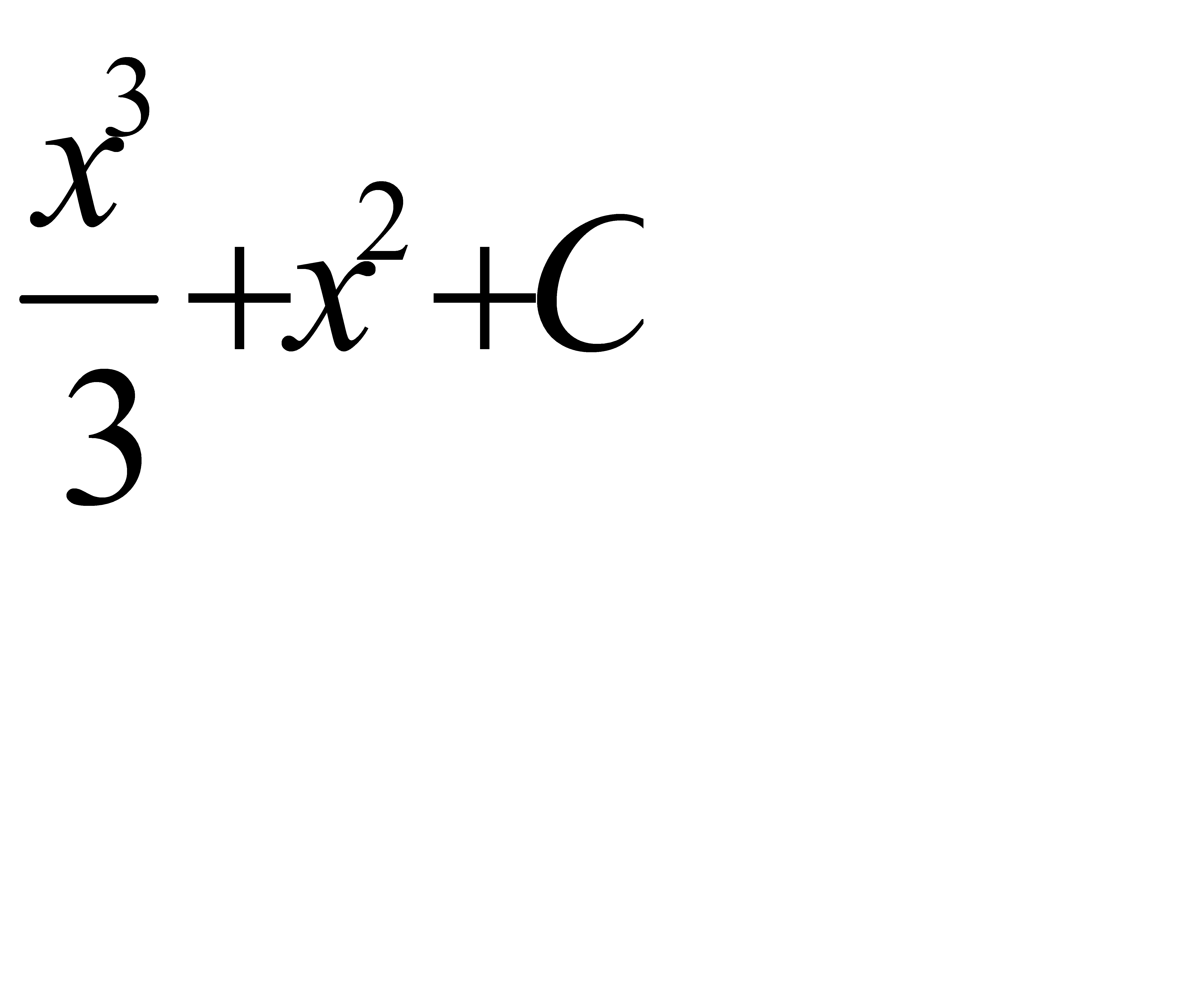 G)
G) 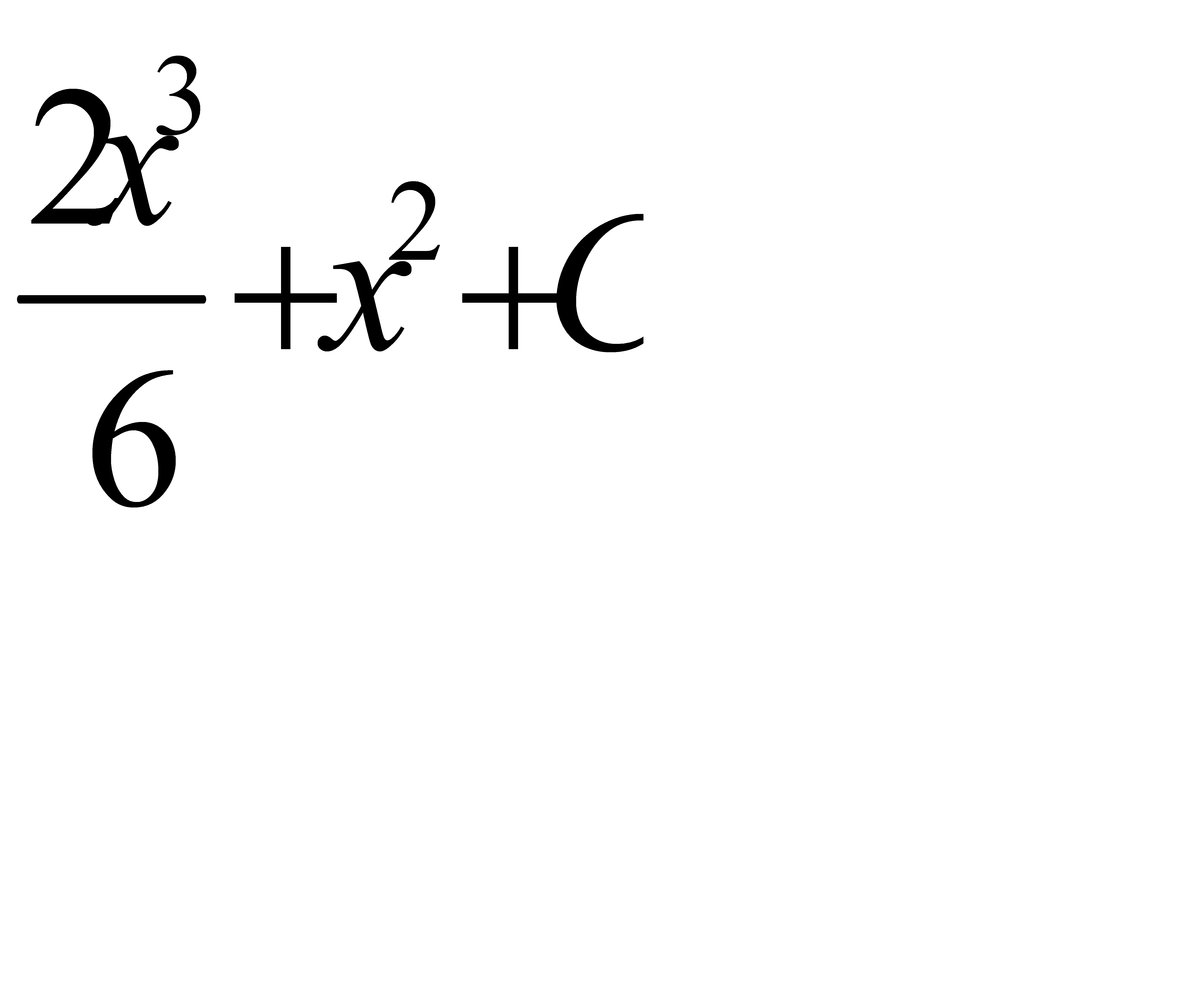 H)
H) 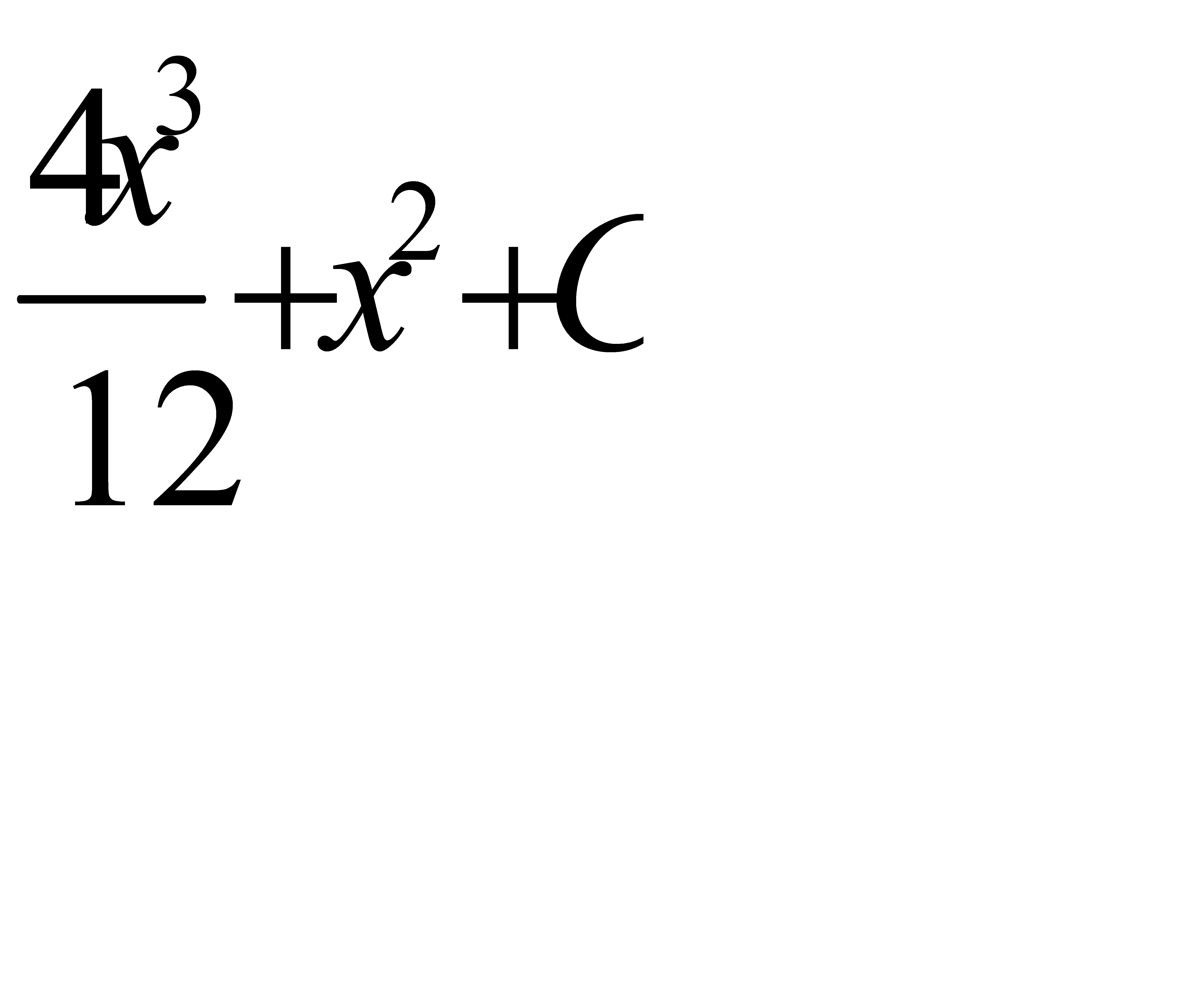
Интегралды табыңыз: 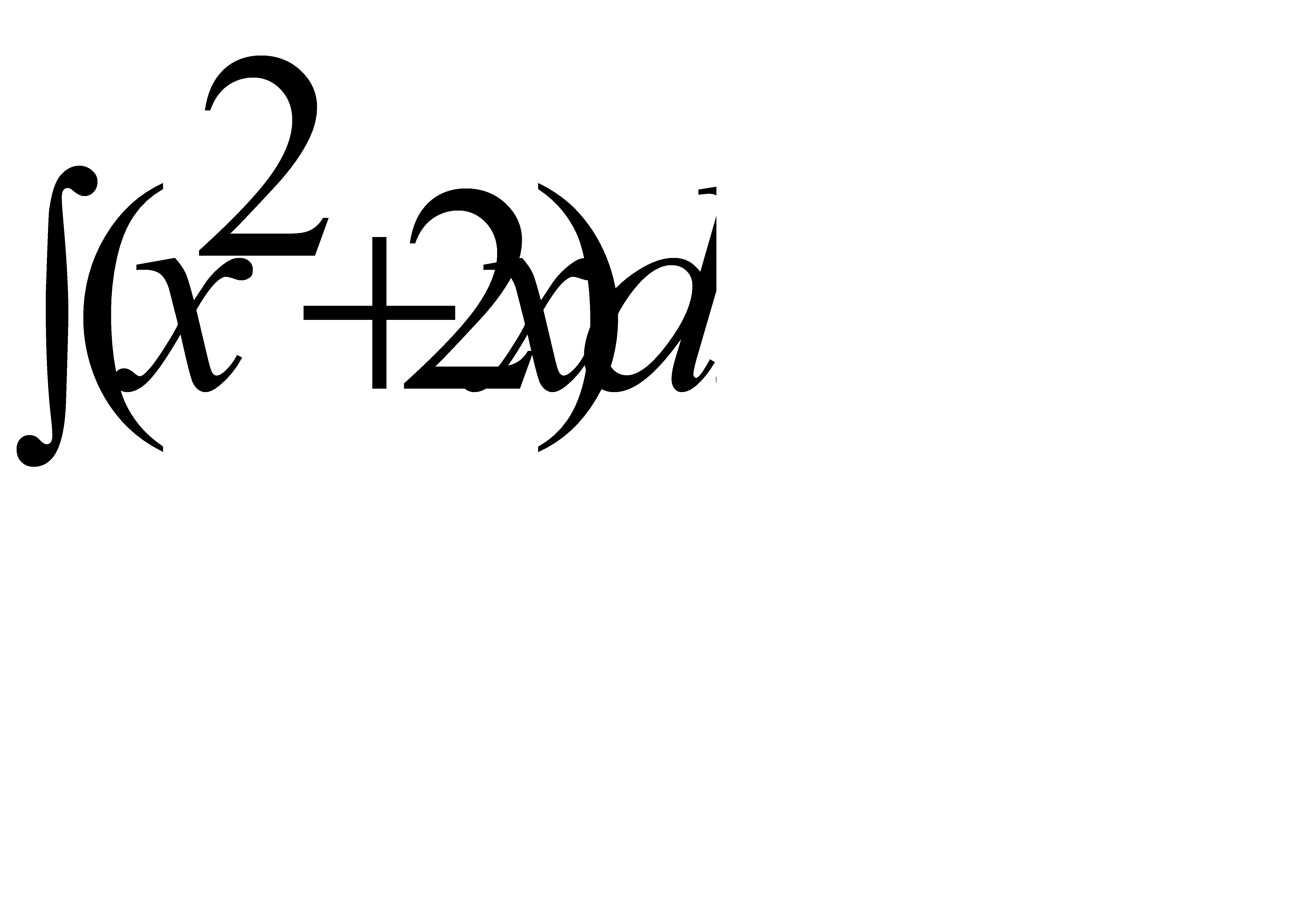 .A)
.A) 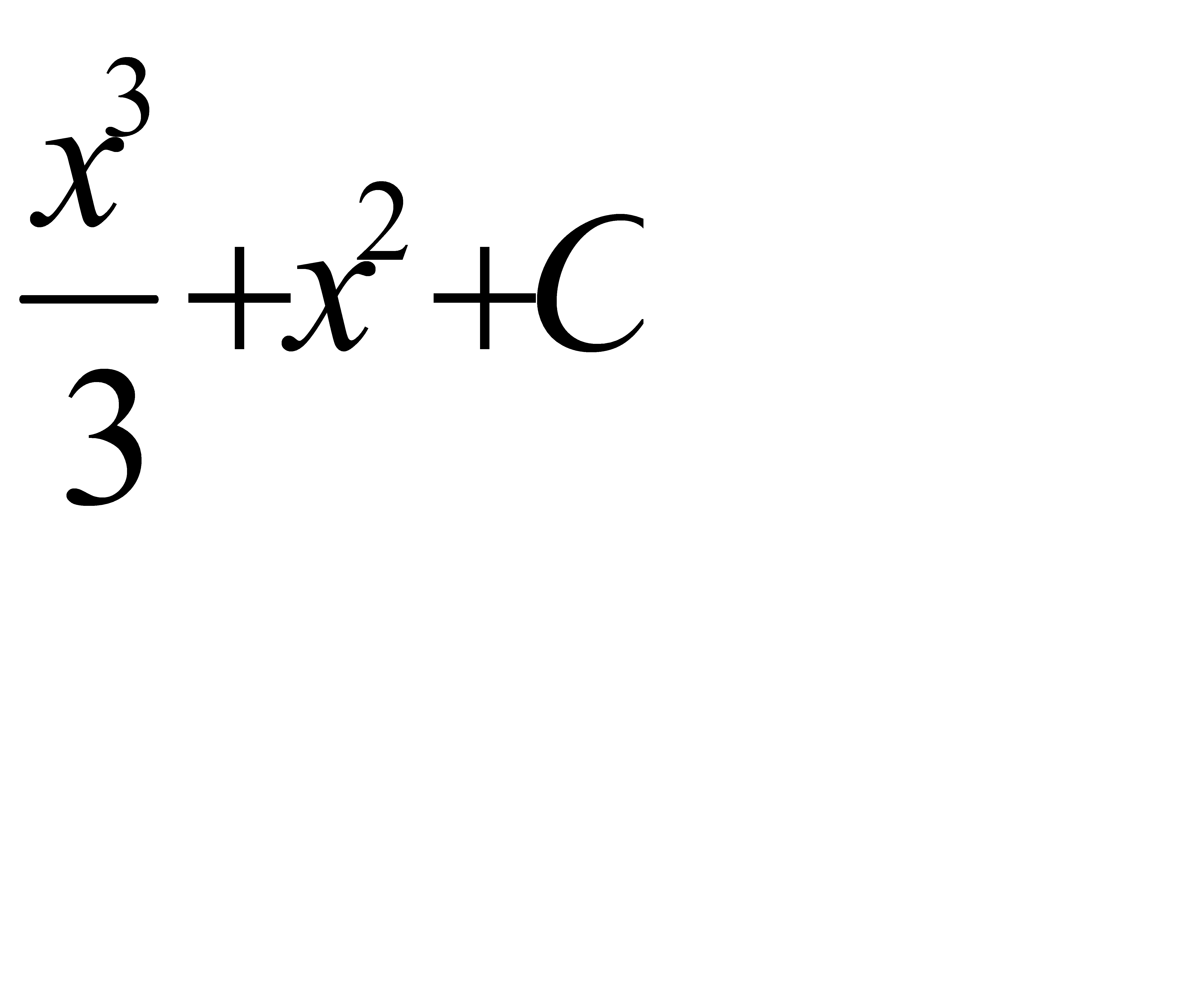 G)
G) 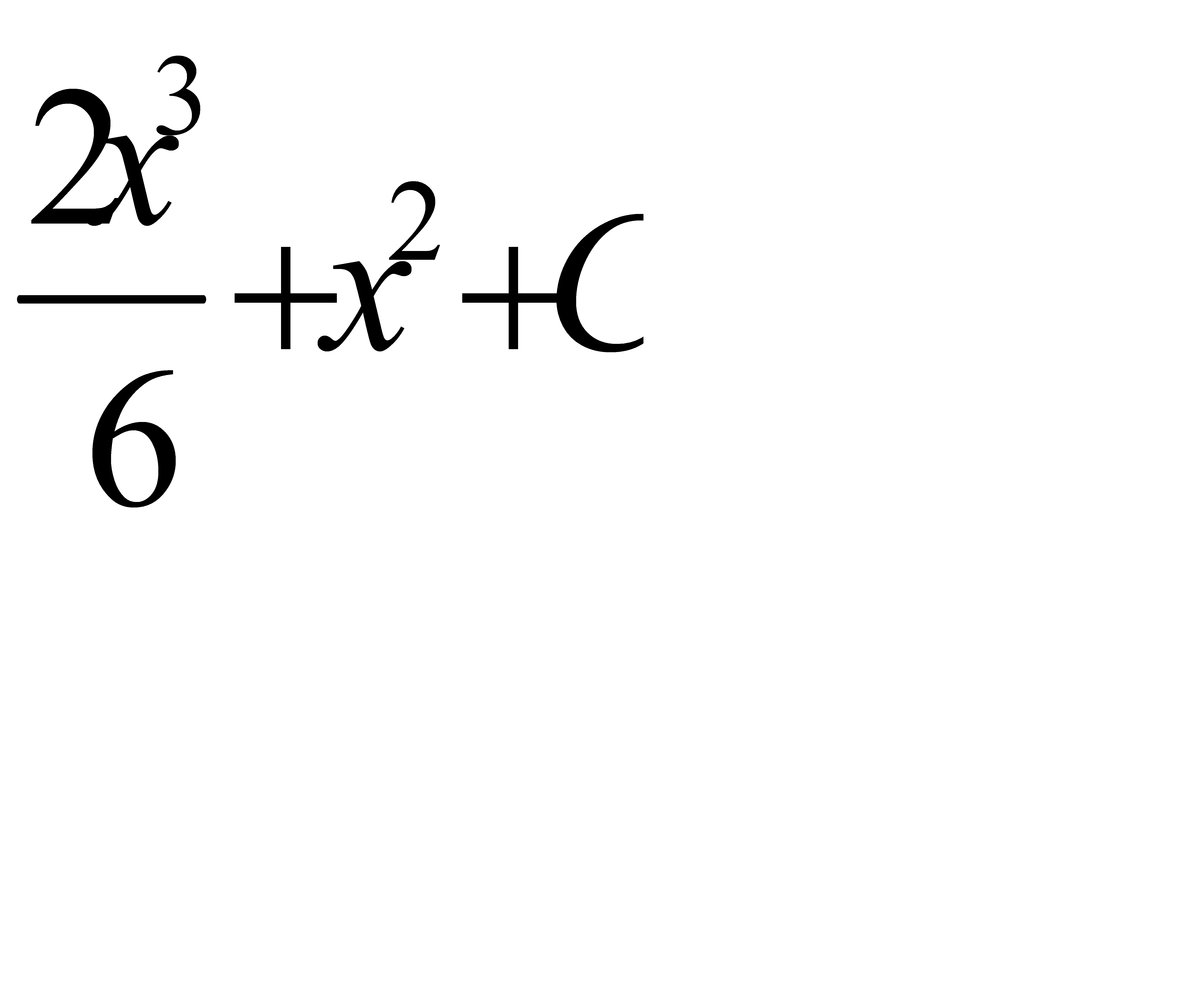 H)
H) 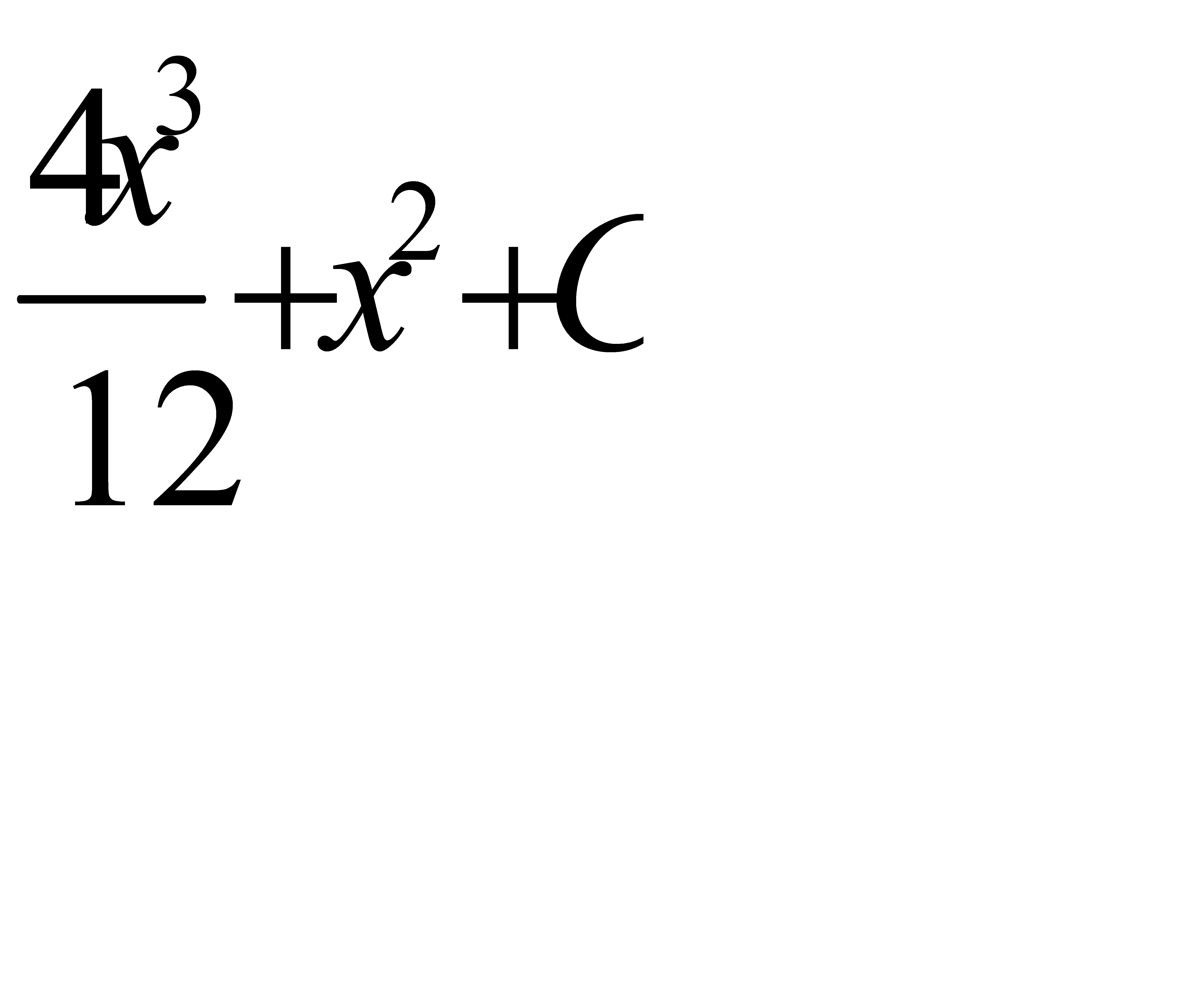
Интегралды табыңыз:  .А)
.А) 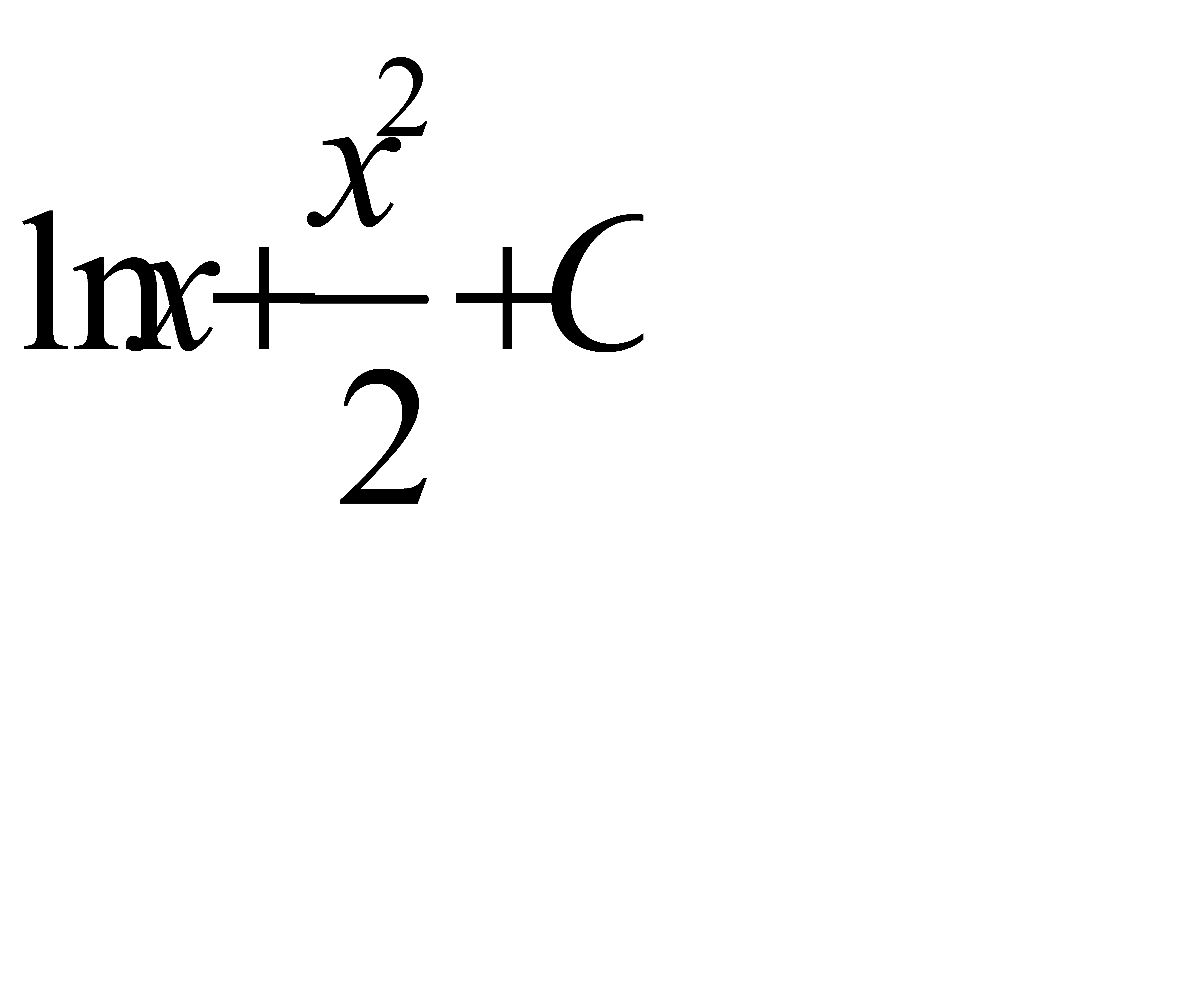 G)
G) 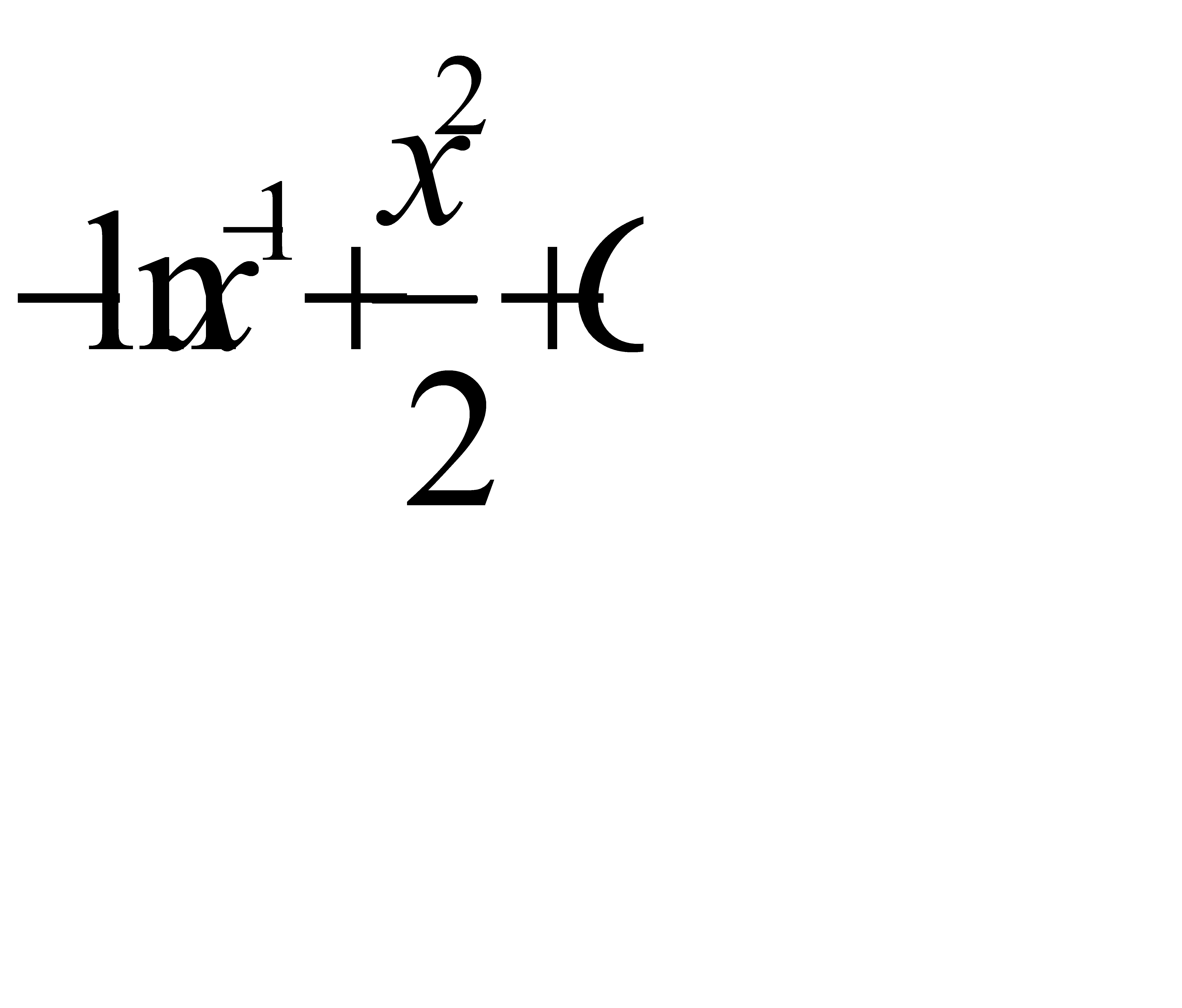 H)
H) 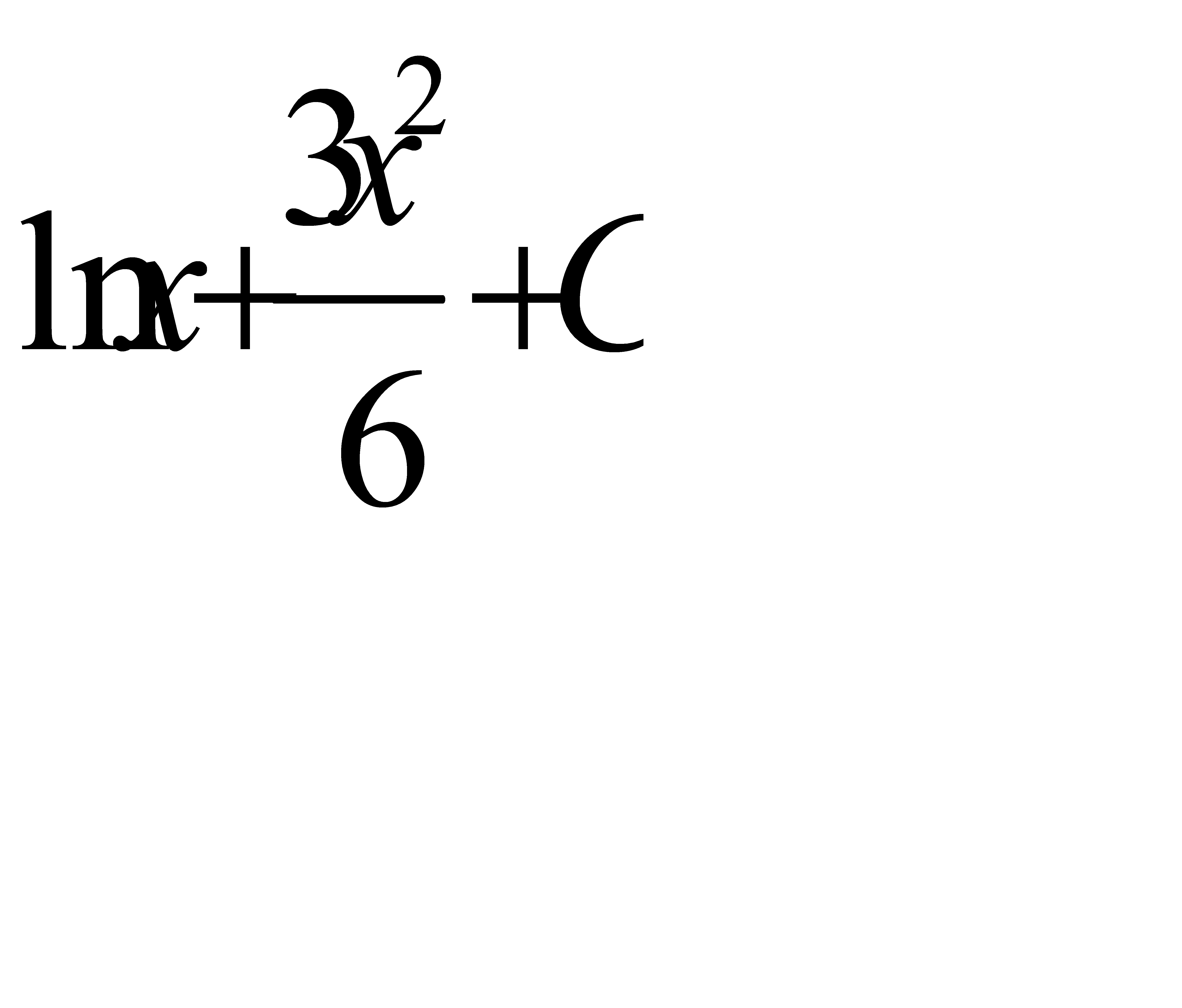
Интегралды табыңыз:  .А)
.А) 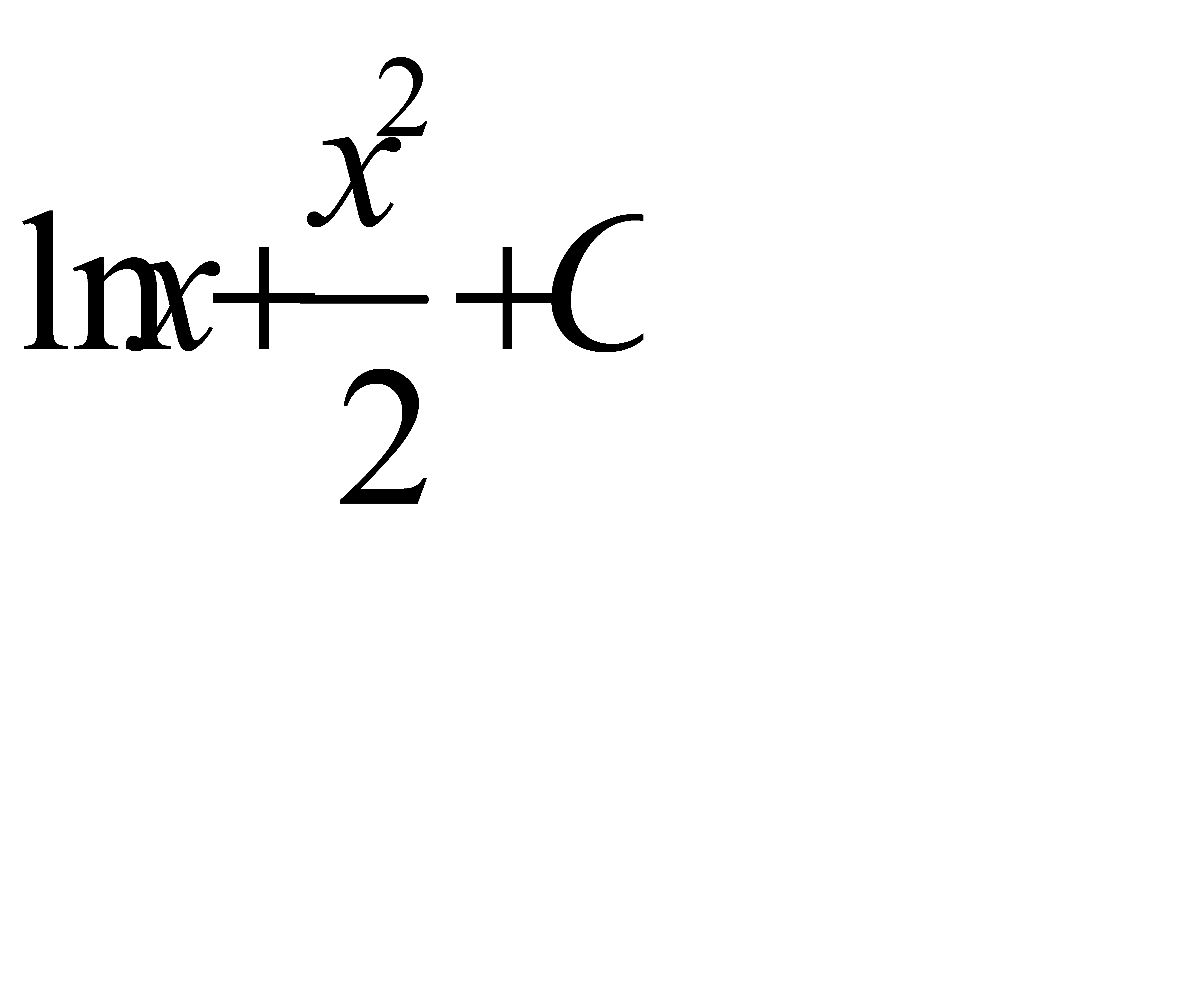 G)
G) 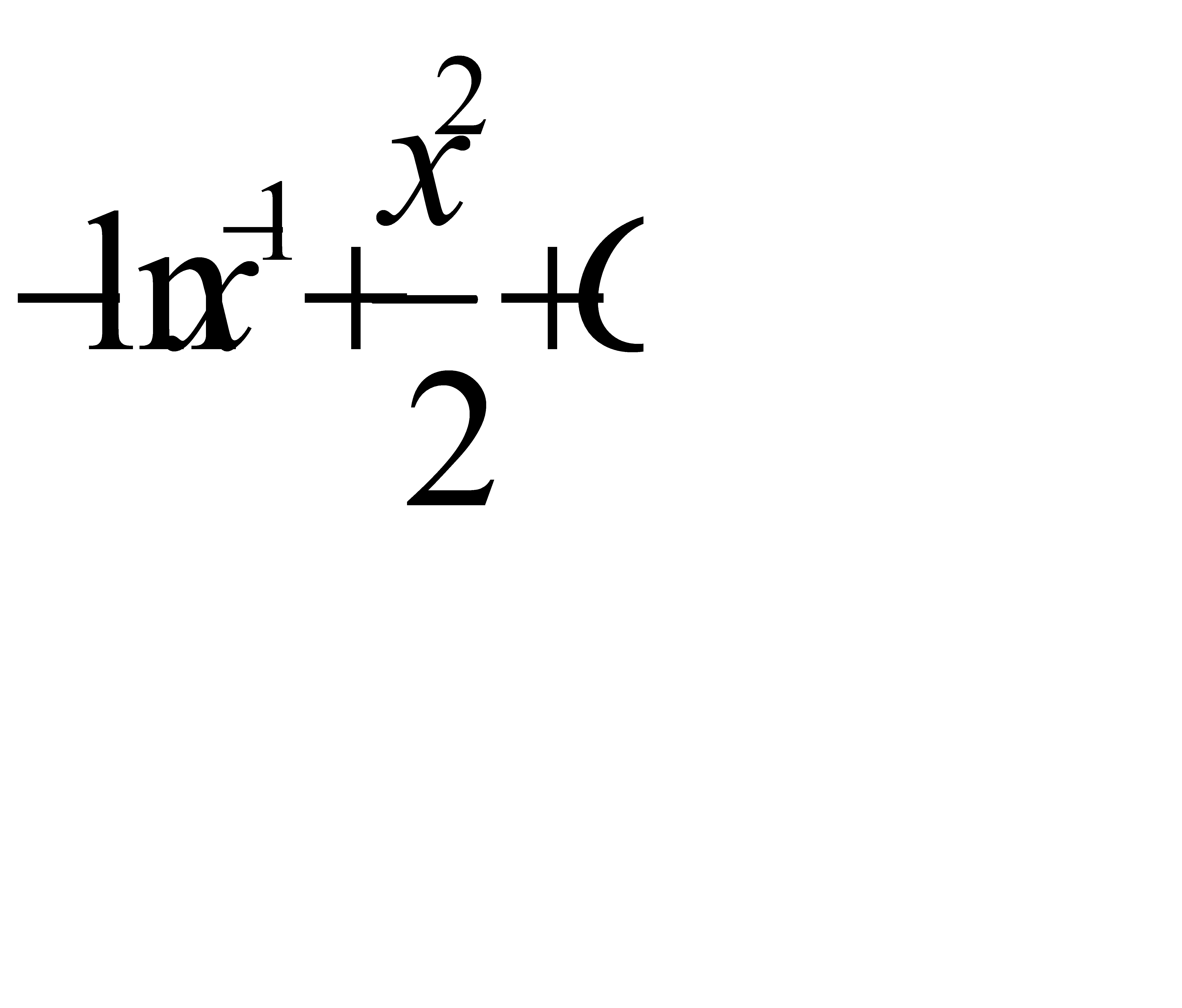 H)
H) 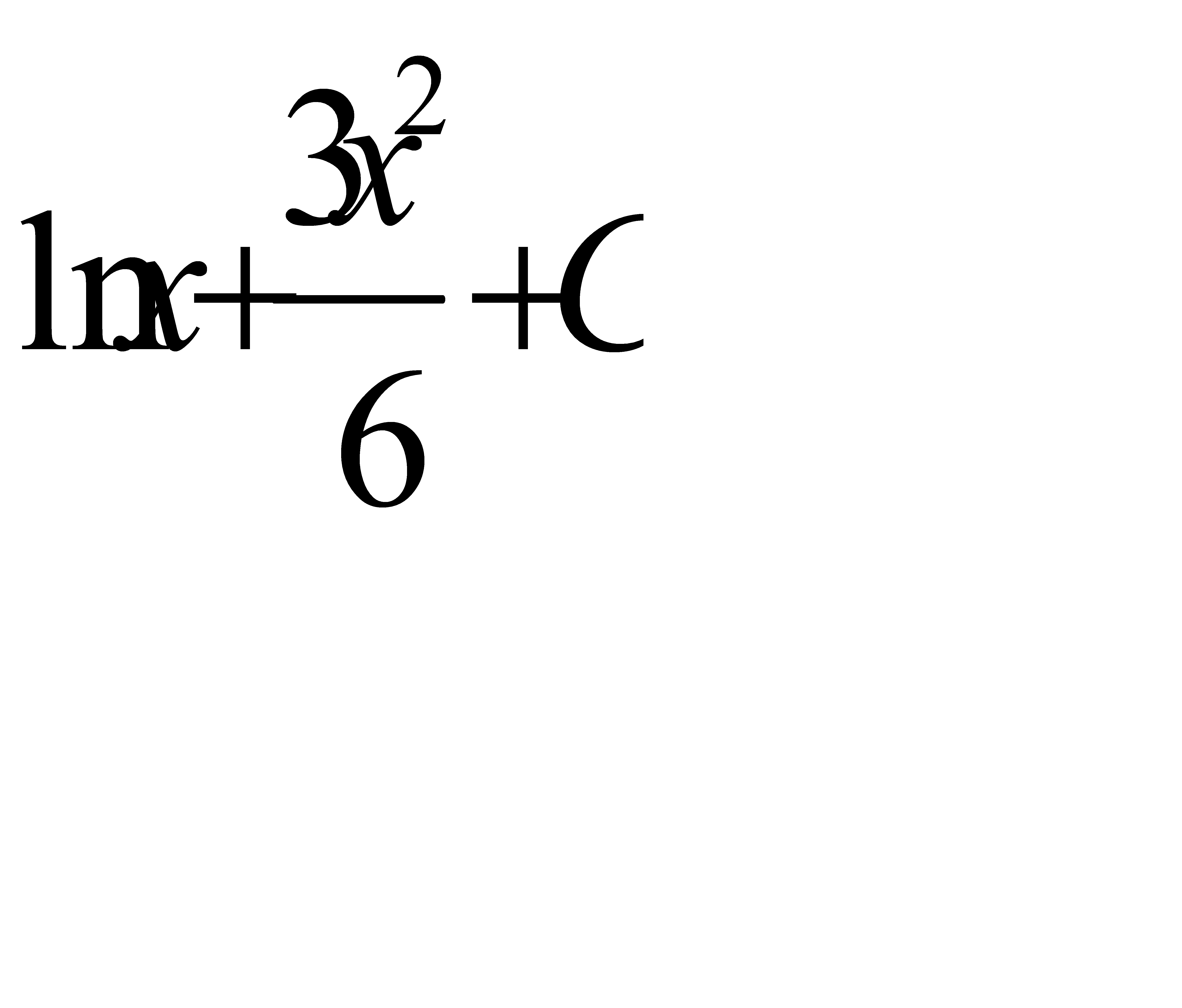
Квадрат матрица:A) 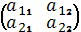 F)
F) 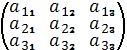 H)
H) 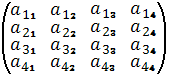
Квадрат үшмүшелікте толық квадратты ажырату тәсілімен табылатын интеграл: B) 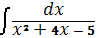 D)
D) 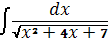 G)
G) 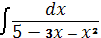
Келесі сызықтармен шектелген фигураның ауданын табу керек: 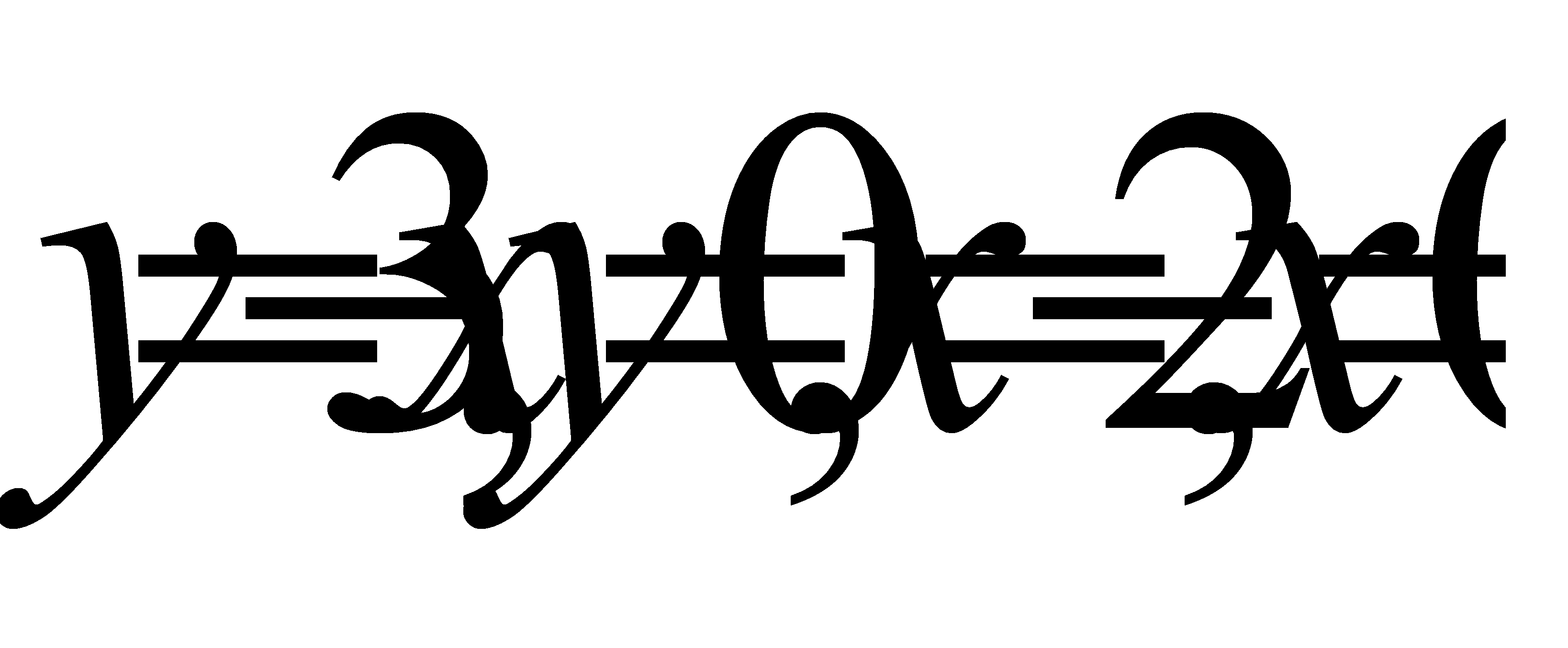 A) 6 C) 12/2 H) 18/3
A) 6 C) 12/2 H) 18/3
Келесі сызықтармен шектелген фигураның ауданын табу керек: 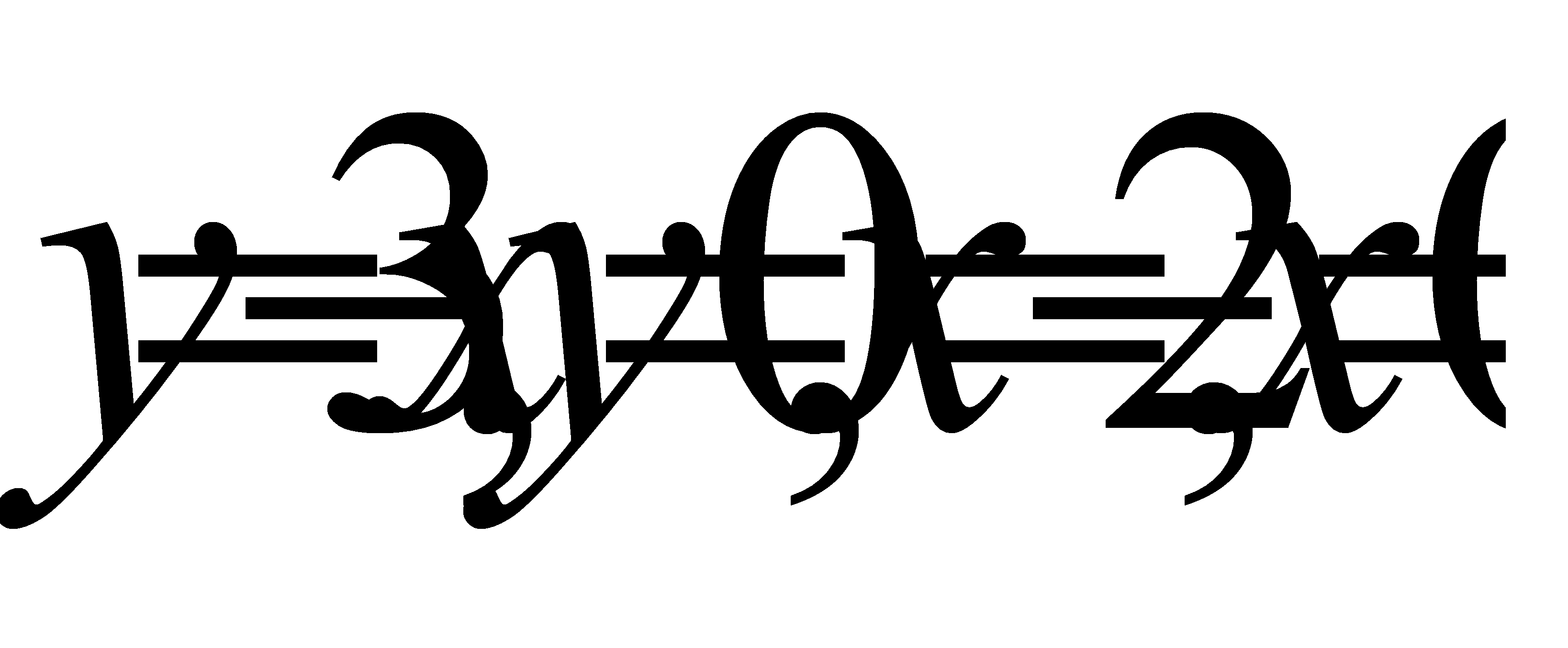 A)6 C)12/2 H) 18/3
A)6 C)12/2 H) 18/3
Келесі сызықтармен шектелген фигураның ауданын табу керек: 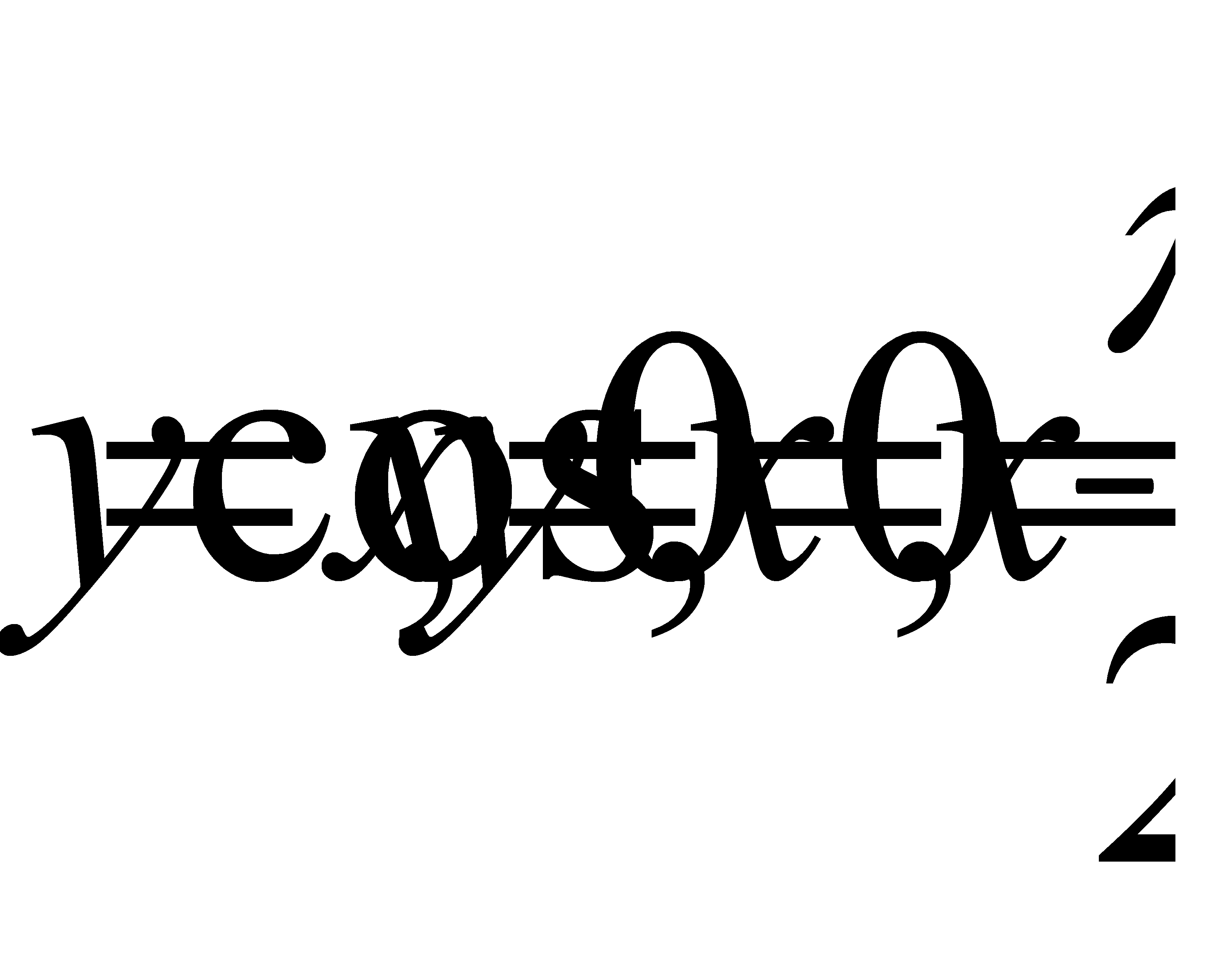 D) 1 G) 2/2 H) 8/8
D) 1 G) 2/2 H) 8/8
Келесі сызықтармен шектелген фигураның ауданын табу керек: 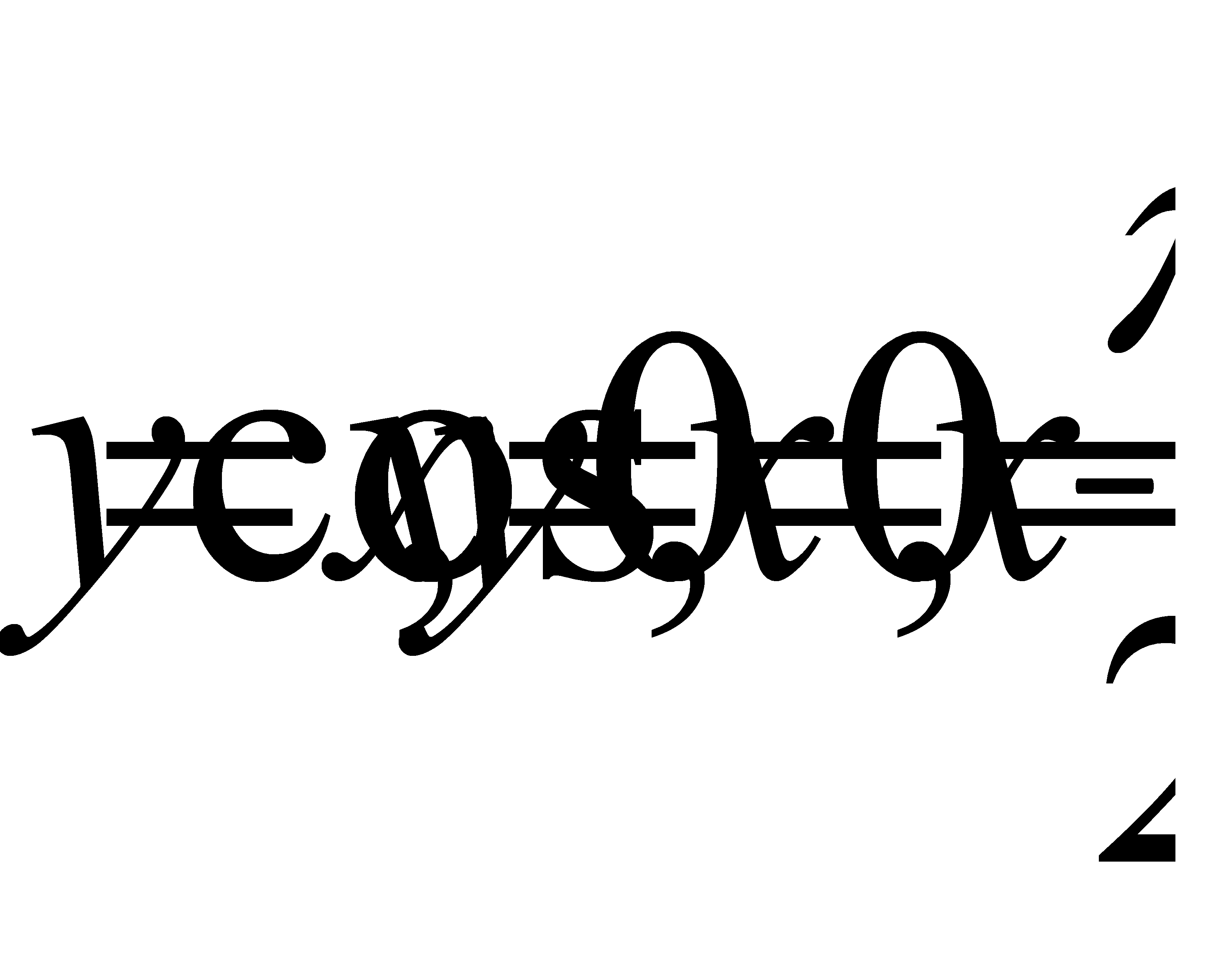 D) 1 G) 2/2 H) 8/8
D) 1 G) 2/2 H) 8/8
Келесі сызықтармен шектелген фигураның ауданын табыңыз: y=5x, x=2, y=0A) 10 G) 40/4 H) 30/3
Келесі сызықтармен шектелген фигураның ауданын табыңыз: y=5x, x=2, y=0A) 10 G) 40/4 H) 30/3
Кошидің радикалдық белгісі бойынша қатар 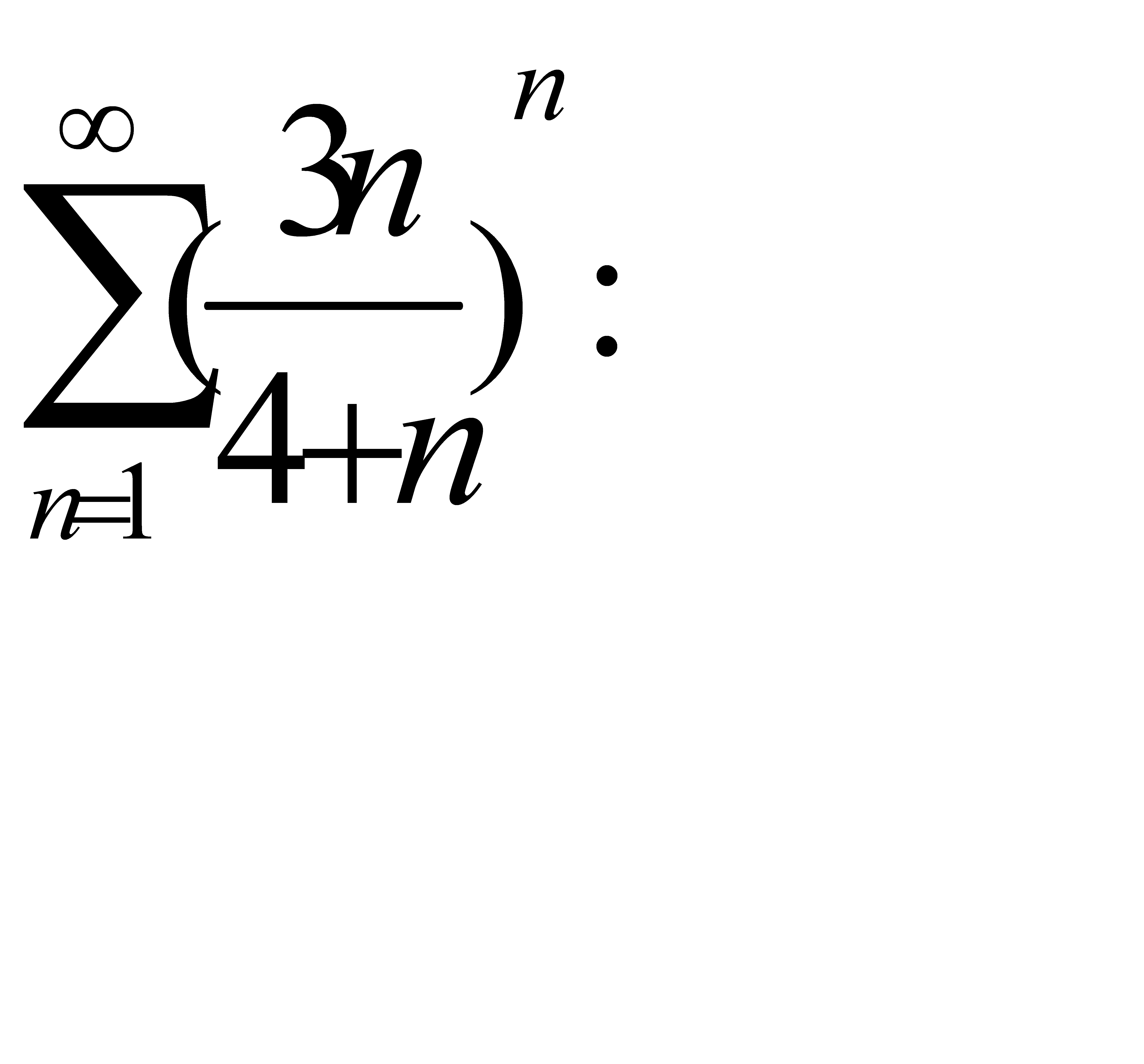 B) жинақсыз G) жинақсыз, өйткені
B) жинақсыз G) жинақсыз, өйткені 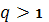 H) жинақсыз, өйткені
H) жинақсыз, өйткені 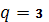
Кошидің радикалдық белгісі бойынша қатар 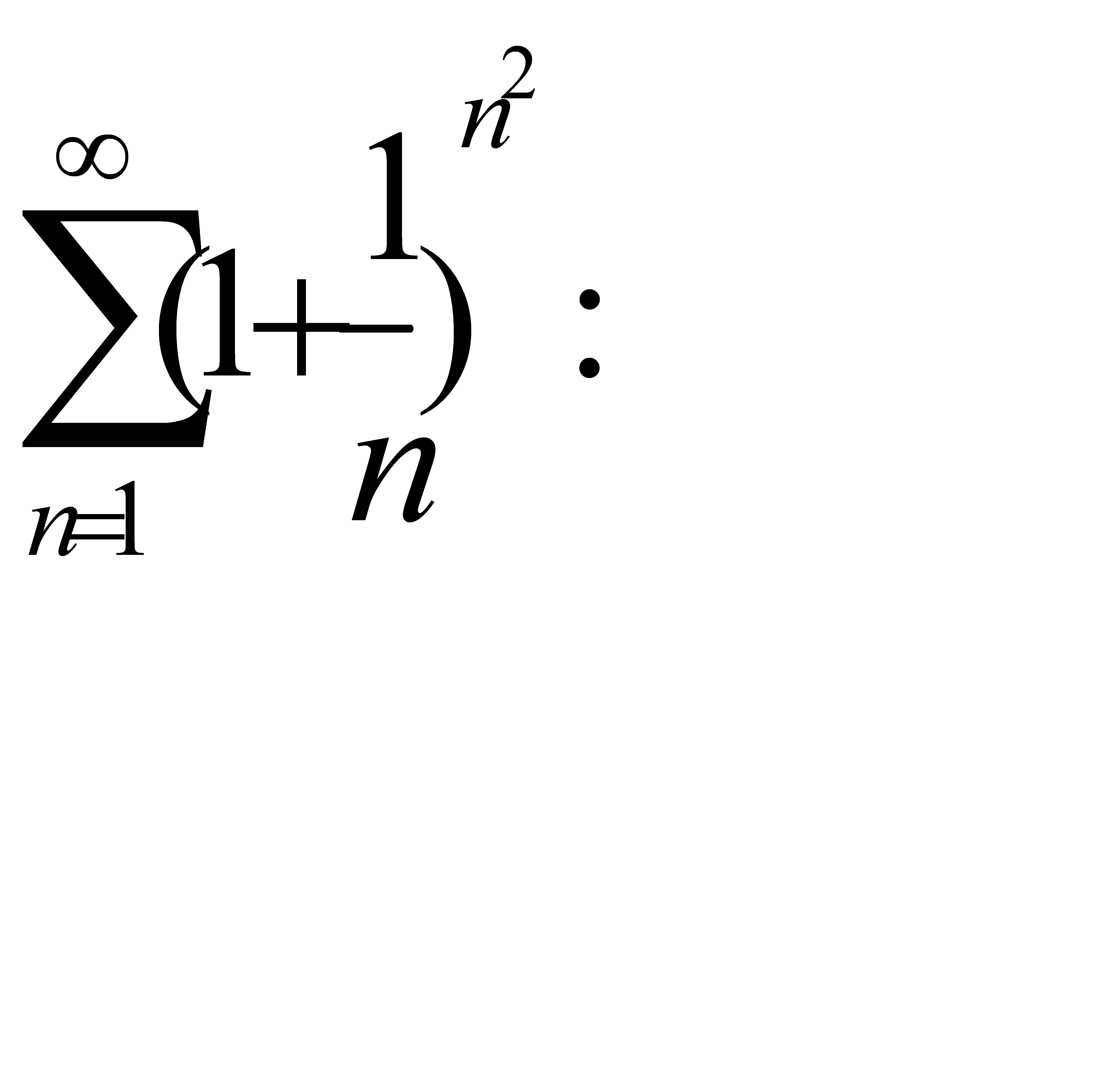 B) жинақсызE) жинақсыз, өйткені
B) жинақсызE) жинақсыз, өйткені 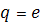 G) жинақсыз, өйткені
G) жинақсыз, өйткені 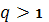
Қатар-матрица:A) 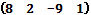 D)
D) 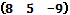 H)
H) 
М (1;-2) нүктесінде 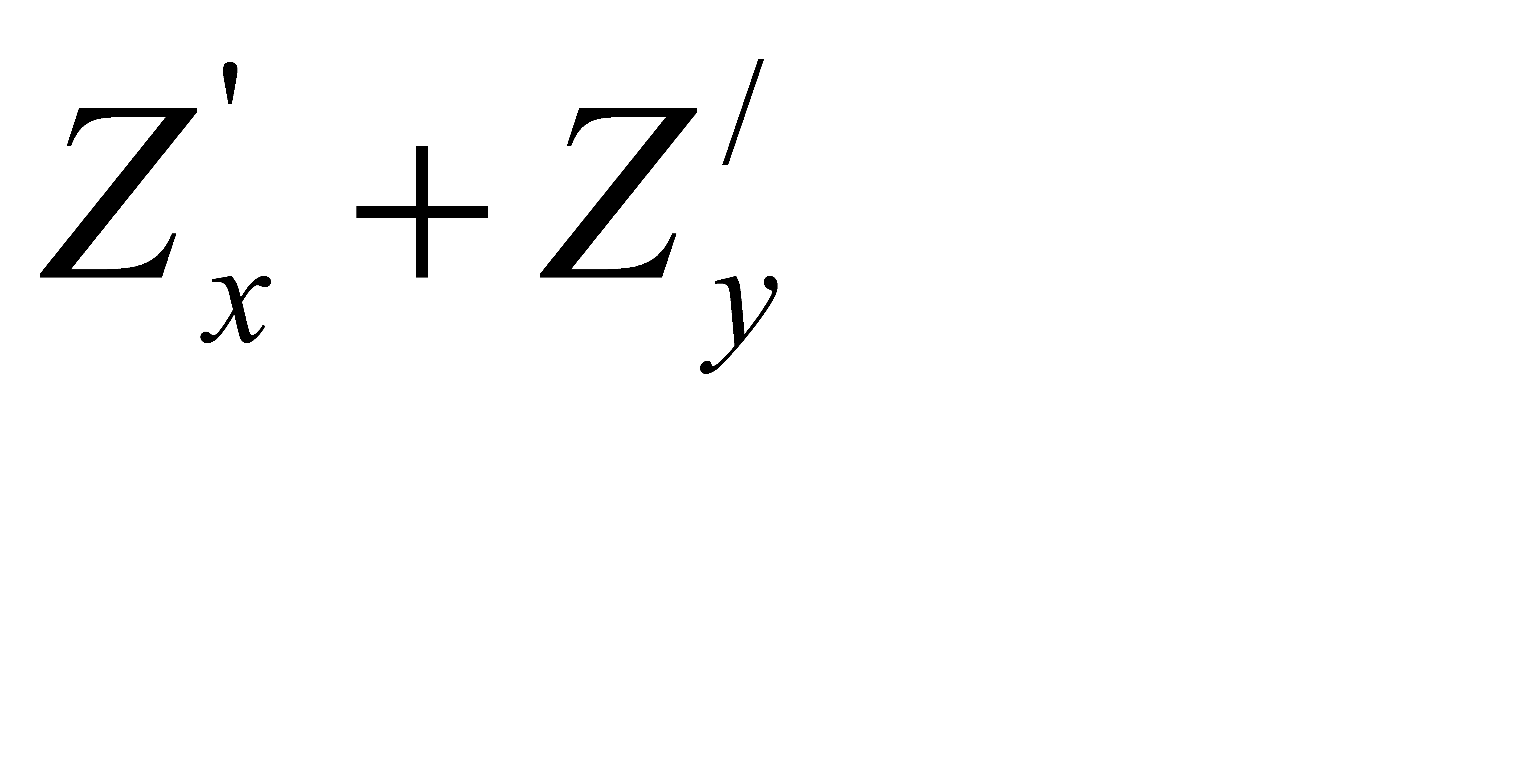 -нің мәні, егер
-нің мәні, егер 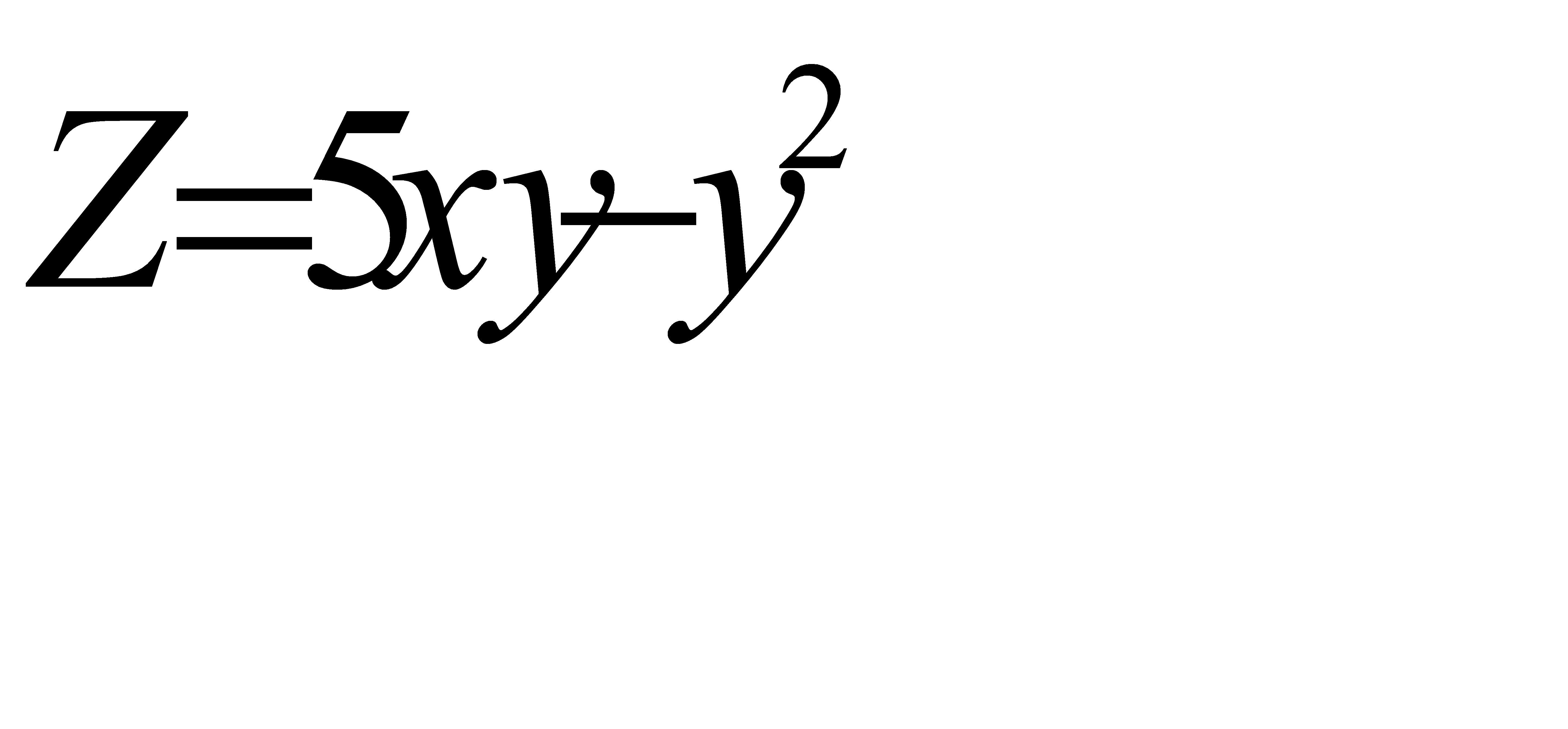 A) -1C) -
A) -1C) -  F) -
F) - 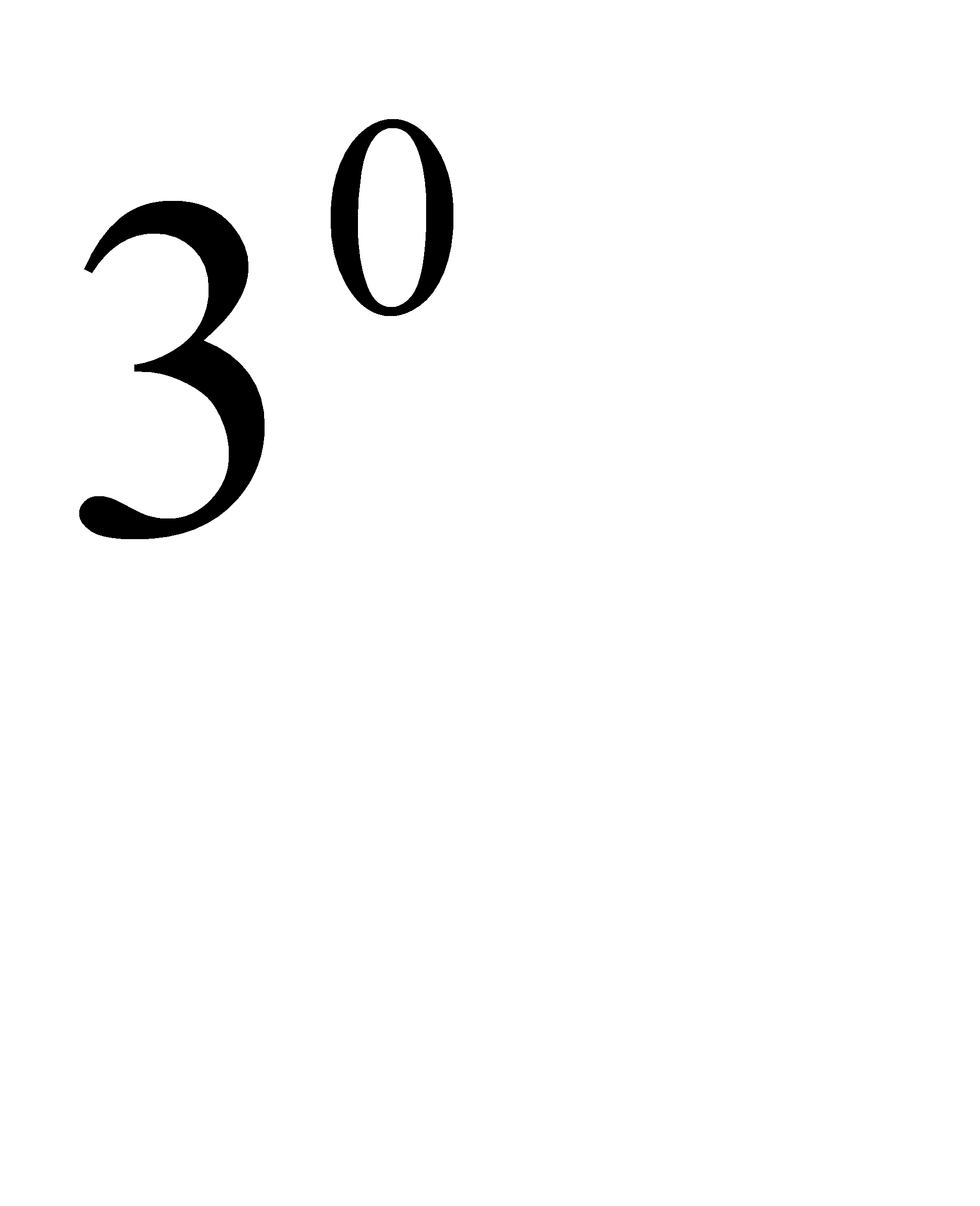
М1(1; 1; -3), М2(-4; 0; 3) екi нүктенiң арақашықтығын тап:А) 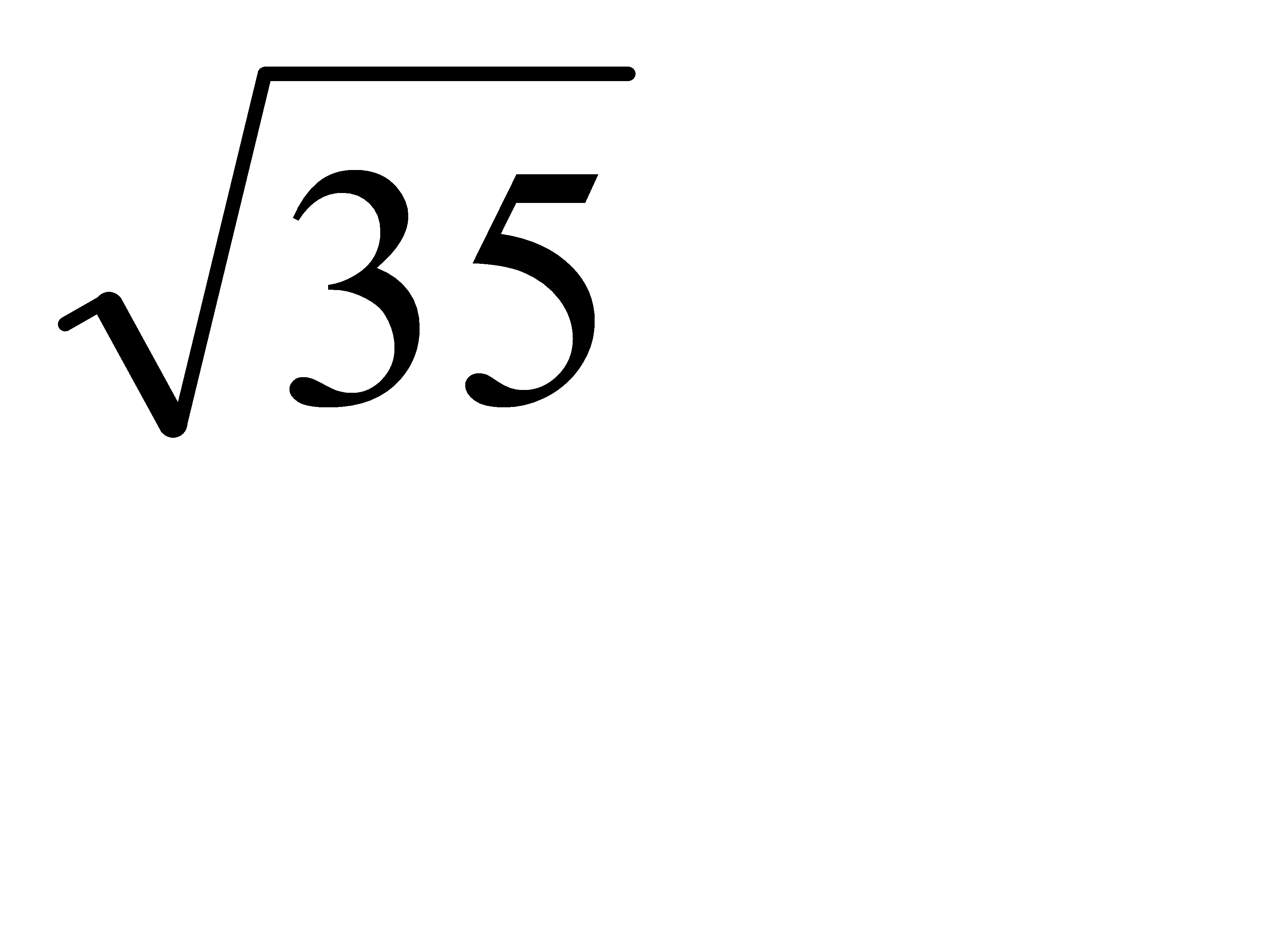 C)
C) 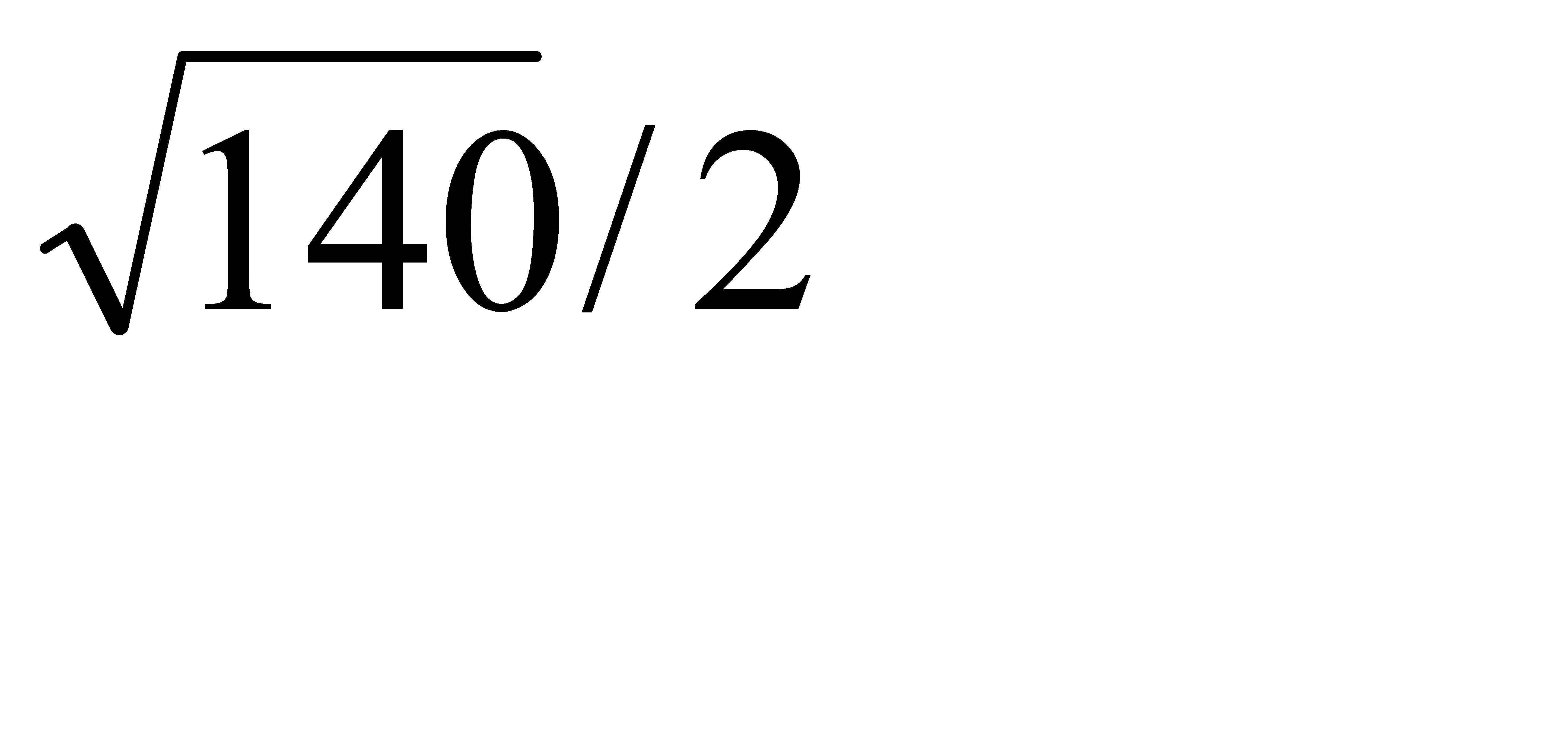 G)
G) 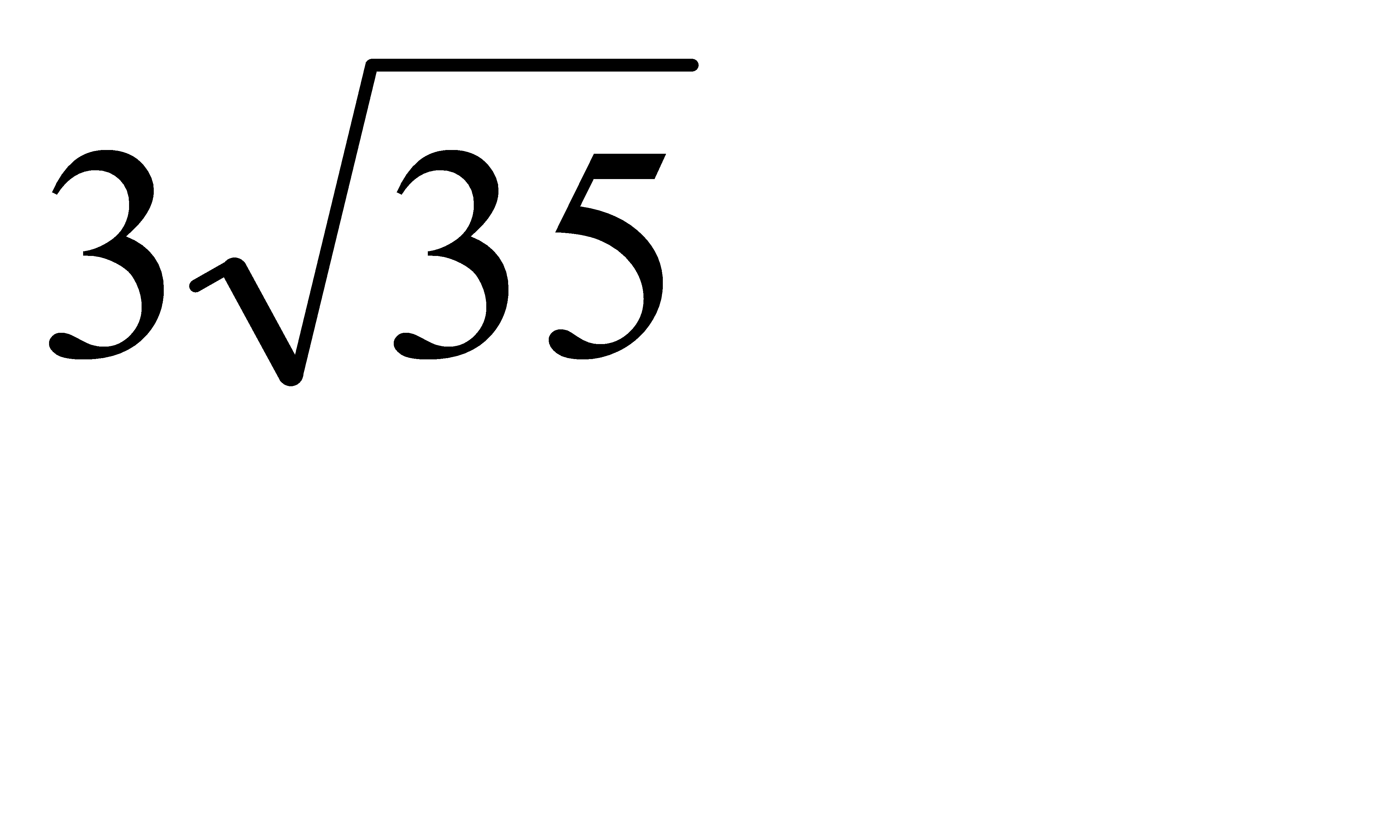
М1(-1; 2; 3), М2(3; -4; 2) екi нүктенiң арақашықтығын тап:А) 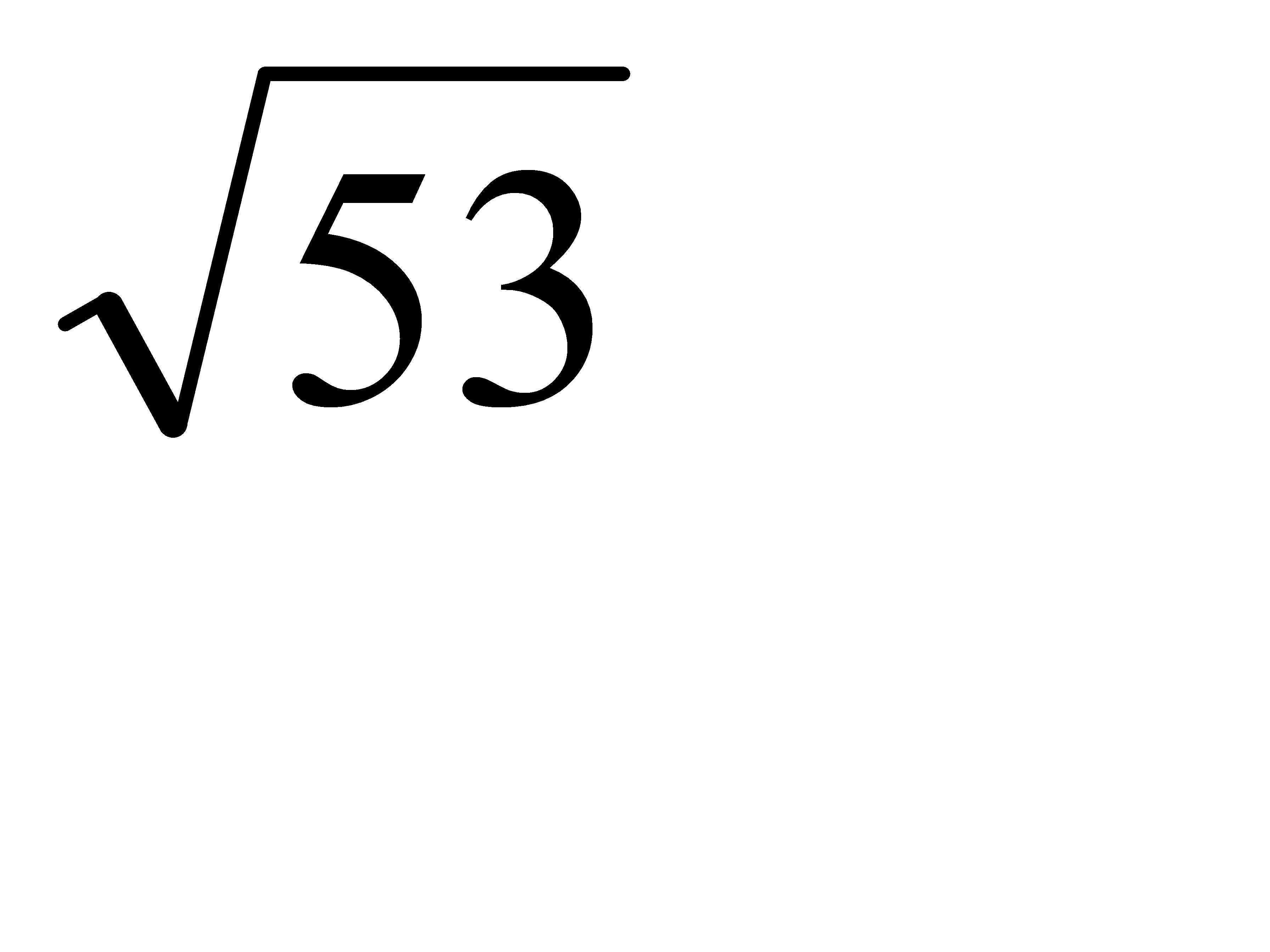 C)
C)  E)
E) 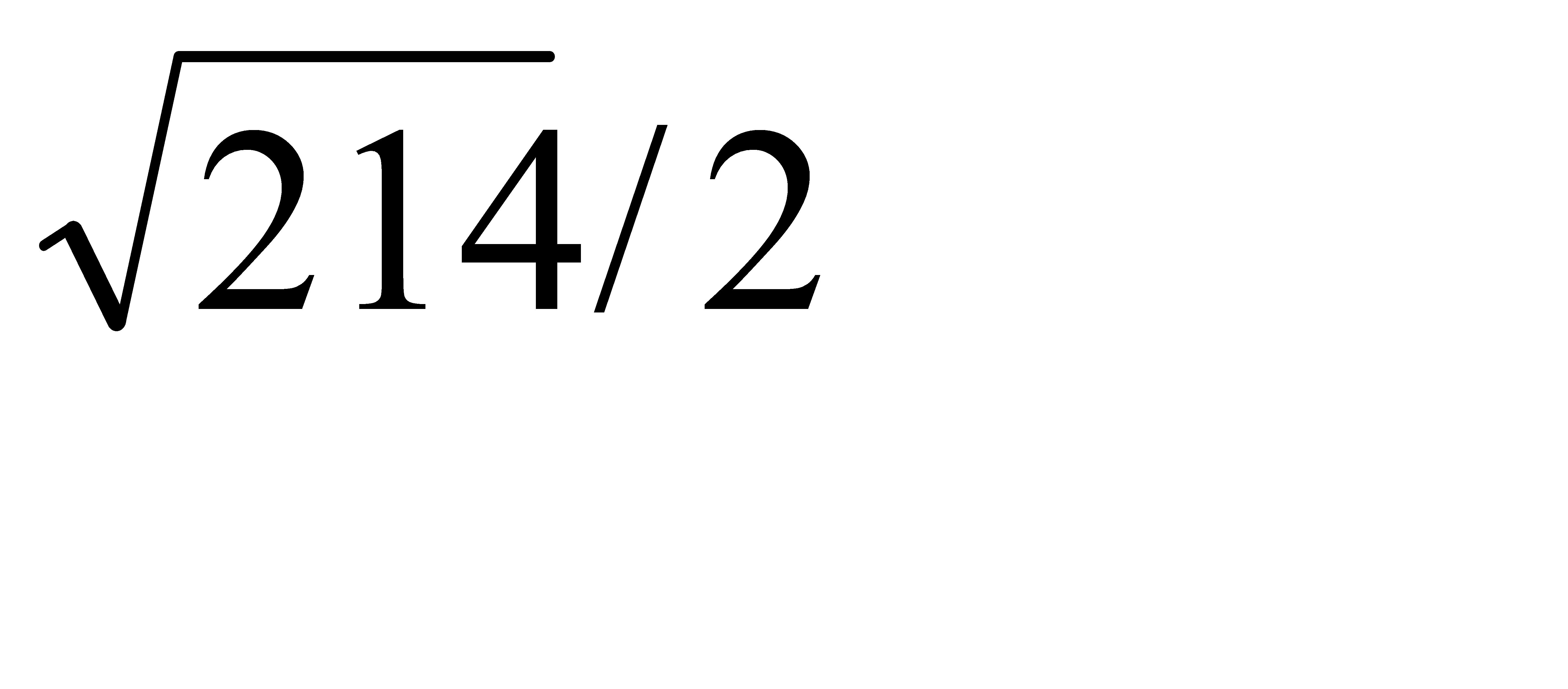
М1(3; 2; 1), М2(4; -3; 2) екi нүктенiң арақашықтығын тап:А) 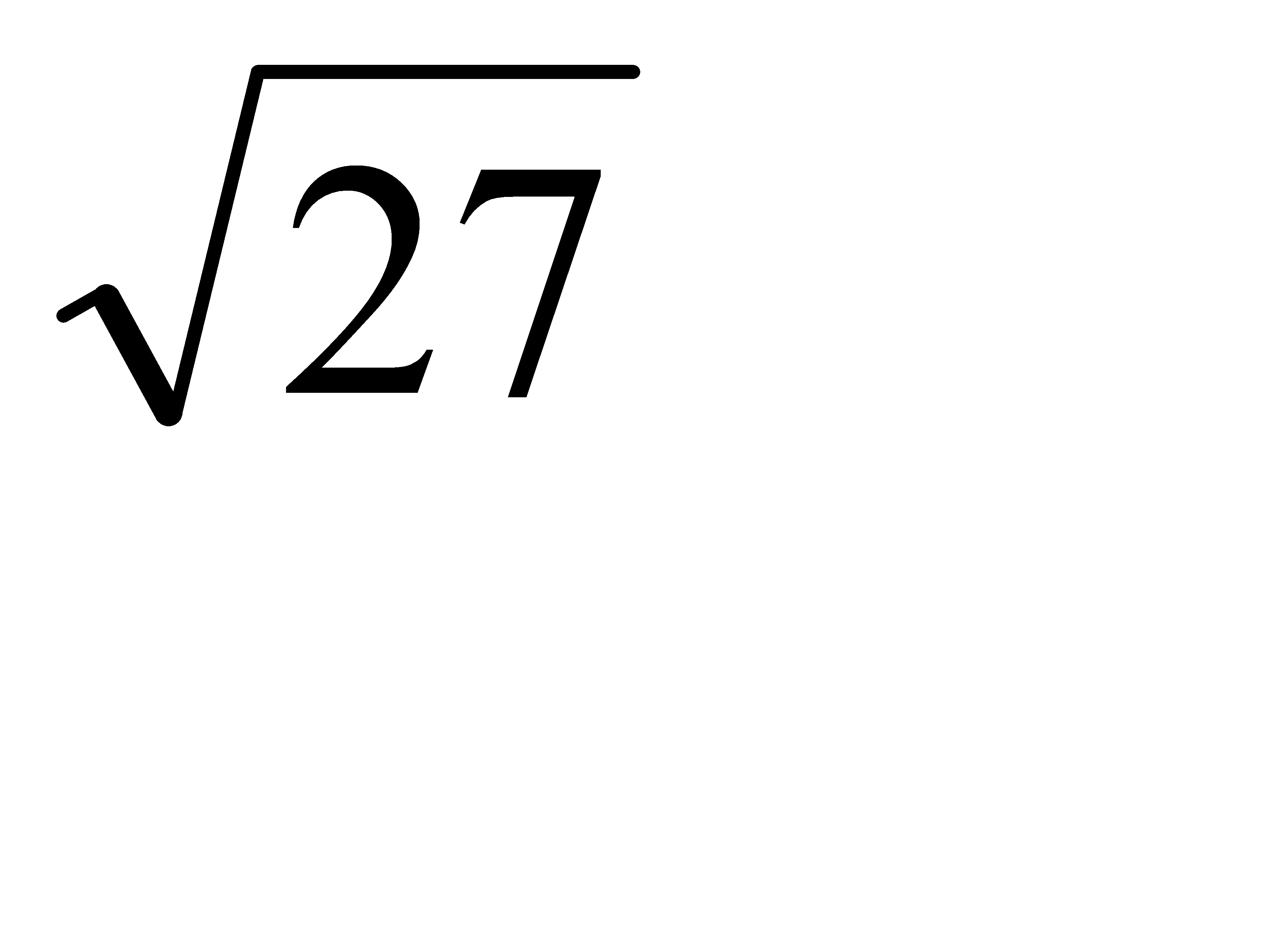 G)
G) 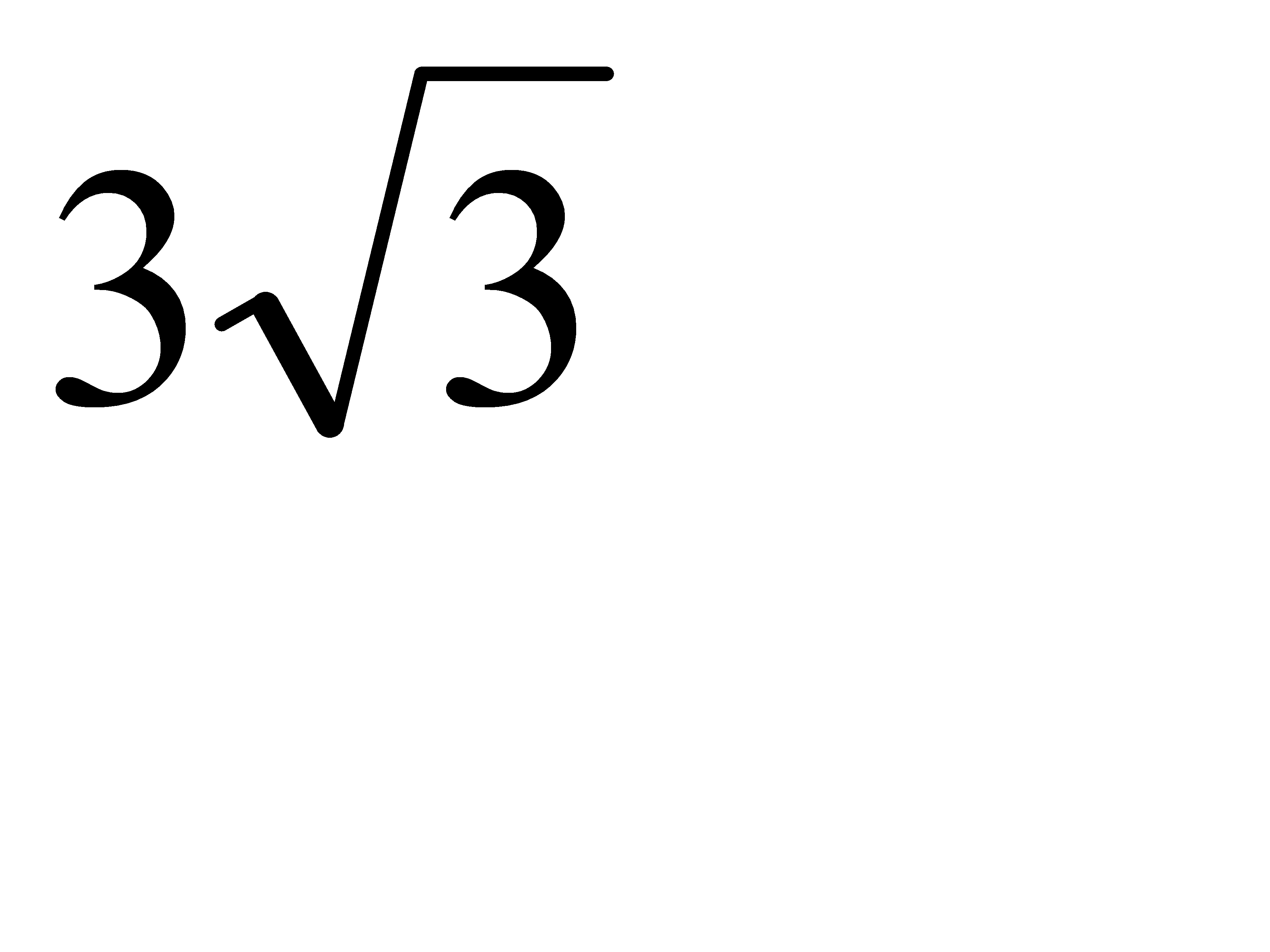 H)
H) 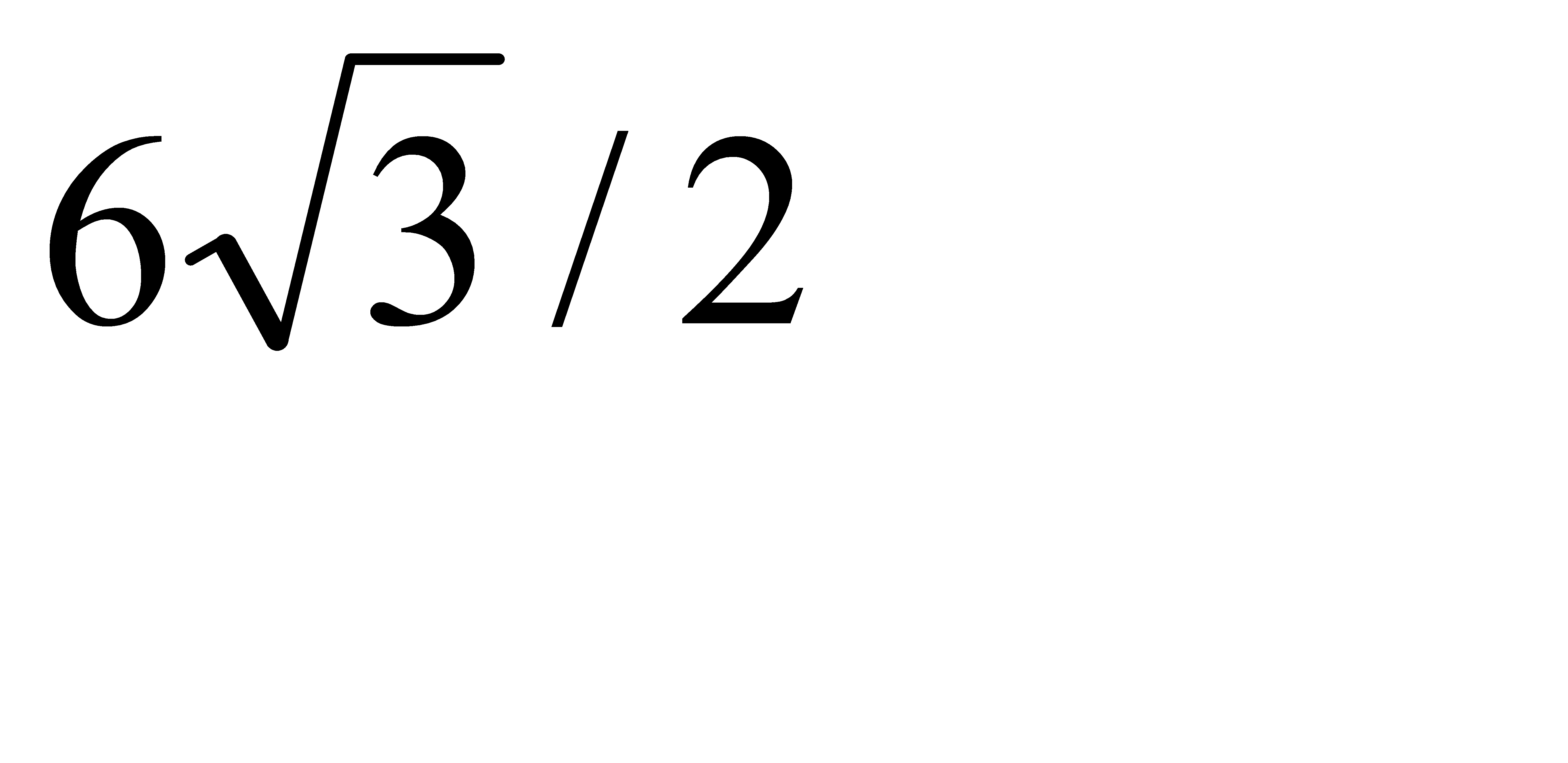
Матрицаның рангы мына жағдайларда өзгермейді:A) кез-келген екі жолын (бағанын) ауыстырғаннан D) кез-келген жолының (бағанының) элементтерін 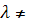 0 санына көбейткеннен F) кез-келген қатардың элементтеріне
0 санына көбейткеннен F) кез-келген қатардың элементтеріне 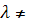 0 санына көбейтілген басқа қатардың элементтерін қосқаннан
0 санына көбейтілген басқа қатардың элементтерін қосқаннан
Мына матрица үшін кері матрицаны табуға болады:A) 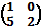 F)
F) 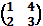 G)
G) 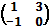
Мына өлшемді матрицалардың айырмасын табуға болады:B) 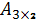 және
және 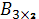 E)
E) 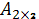 және
және 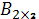 H)
H) 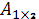 және
және 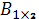
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|