
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
функциясының нүктесіндегі туындысын табыңыздар. 1 страница
Формулы скалярного произведения векторов заданных координатами
a · b = ax · bx + ay · by
Формулы определения координат вектора заданного координатами его начальной и конечной точки AB = {Bx - Ax ; By - Ay}
Формулы длины вектора |a| = √ax2 + ay2
Формулы вычисления смешанного произведения векторов
a = {ax; ay; az}, b = {bx; by; bz} и c = {cx; cy; cz}
| a · [b × c] = | ax | ay | az |
| bx | by | bz | |
| cx | cy | cz | |
Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.
| cos α = | a·b |
| |a|·|b| |
Векторное произведение двух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат - это вектор, значение которого можно вычислить, используя следующие формулы:
| a × b = | i | j | k | = i(aybz - azby) - j(axbz - azbx) + k(axby - aybx) |
| ax | ay | az | ||
| bx | by | bz |
a × b = {aybz - azby; azbx - axbz; axby - aybx}
Три вектора компланарны если их смешанное произведение равно нулю.
Условия коллинеарности векторов
| ax | = | ay | . |
| bx | by |
середины отрезка АВ с концами 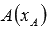 и
и 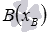 имеет вид
имеет вид 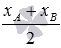 .
.
расстояние от точки 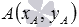 до точки
до точки 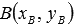 на плоскости находится через координаты точек по формуле
на плоскости находится через координаты точек по формуле 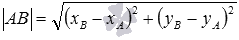 .
.
длина отрезка прямой| AB| = 
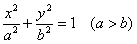 – каноническое уравнение эллипса Для эллипса: c 2 = a2 – b2 . х=
– каноническое уравнение эллипса Для эллипса: c 2 = a2 – b2 . х= 
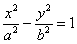 – каноническое уравнение гиперболы; гиперболы называют отношение
– каноническое уравнение гиперболы; гиперболы называют отношение 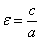
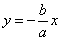 ε=
ε= 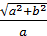 Для гиперболы: c2 = a2 + b2 .
Для гиперболы: c2 = a2 + b2 .
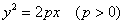 – каноническое уравнение параболы;
– каноническое уравнение параболы;
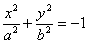 – мнимый эллипс;
– мнимый эллипс;
$$$001
Пусть 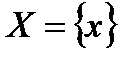 -ограниченное множество вещественных чисел. Число
-ограниченное множество вещественных чисел. Число  называется нижней гранью множества X, если :
называется нижней гранью множества X, если :
A) 1)каждое 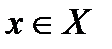 удовлетворяет неравенству
удовлетворяет неравенству 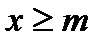
2)каковы ни было 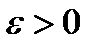 , существует
, существует 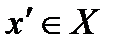 такое , что
такое , что 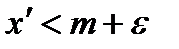
B) каждое 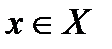 удовлетворяет неравенству
удовлетворяет неравенству 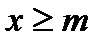
C) каковы ни было 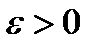 , существует
, существует 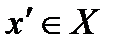 такое , что
такое , что 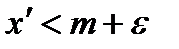
D) каждое 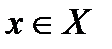 удовлетворяет неравенству
удовлетворяет неравенству 
E) каждое 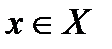 удовлетворяет неравенству
удовлетворяет неравенству 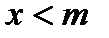
F) каковы ни было 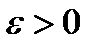 , существует
, существует 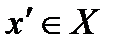 такое , что
такое , что 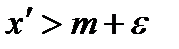
G) 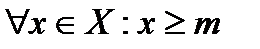 и
и 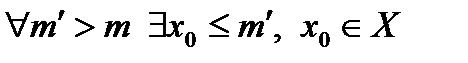
H) Число 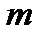 - наибольшая из всех нижних граней ограниченного снизу множества X
- наибольшая из всех нижних граней ограниченного снизу множества X
{Правильный ответ} = A, G, H
$$$002
Пусть 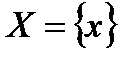 -ограниченное множество вещественных чисел. Число
-ограниченное множество вещественных чисел. Число 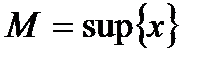 называется верхней гранью множества X, если :
называется верхней гранью множества X, если :
A) 1)каждое 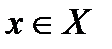 удовлетворяет неравенству
удовлетворяет неравенству 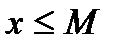
2)каковы ни было 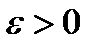 , существует
, существует 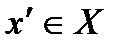 такое , что
такое , что 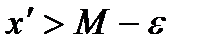
B) каждое 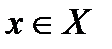 удовлетворяет неравенству
удовлетворяет неравенству 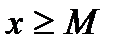
C) каковы ни было 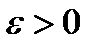 , существует
, существует 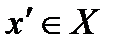 такое , что
такое , что 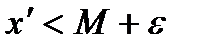
D) каждое 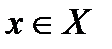 удовлетворяет неравенству
удовлетворяет неравенству 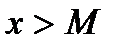
E) каждое 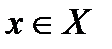 удовлетворяет неравенству
удовлетворяет неравенству 
F) каковы ни было 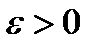 , существует
, существует 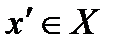 такое , что
такое , что 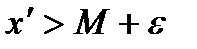
G)  и
и 
H) Число M – наименьшая из всех верхних граней ограниченного сверху множества X .
{Правильный ответ} = A, G, H
$$$001
Числовая последовательность сходится, если она:
A) ограничена
B) не ограничена
C) монотонно возрастает и ограничена снизу
D) монотонно не убывает и ограничена сверху
Е) монотонно убывает и ограничена сверху
F) ограничена снизу и сверху и является монотонной
G) 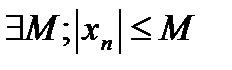 и является монотонной
и является монотонной
H) ограничена снизу
{Правильный ответ}= D, F,G
$$$002
Бесконечно большие последовательности:
A) 
B) 
C) 
D) 
E) 
F) n
G) lnn
H) ln1
{Правильный ответ}=C, F, G
$$$003
Бесконечно малые последовательности:
A) 
B) 
C) 
D) 
E) 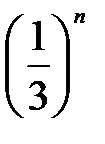
F) sin n
G) 
H) cos n
{Правильный ответ}=B, E, G
$$$004
Последовательность 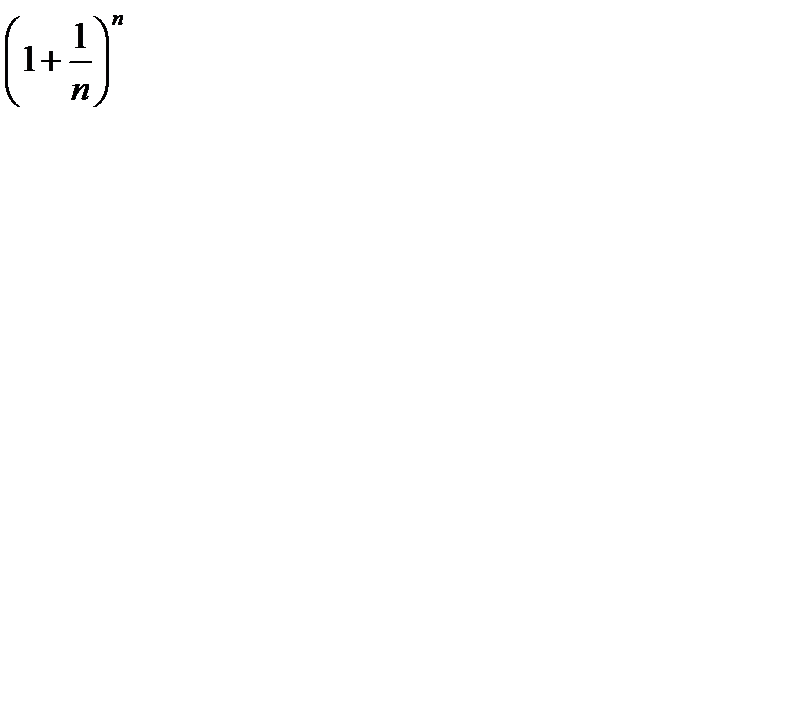 :
:
A) монотонно возрастает
B) монотонно не возрастает
C) монотонно убывает
D) монотонно не убывает
E) не является монотонной
F) монотонно возрастает и ограничена
G) 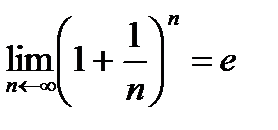
H) равен единице
{Правильный ответ}=A, F, G
$$$005
Последовательность, являющейся подпоследовательностью последовательности  :
:
A) 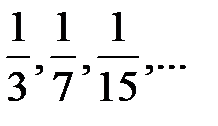
B) 
C) 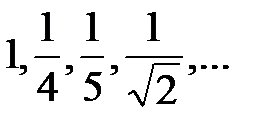
D) 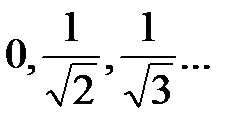
E) 
F) 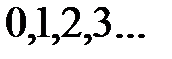
G) 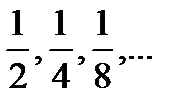
H) 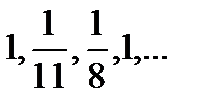
{Правильный ответ}= B, E, G
$$$006
 равен:
равен:
A) 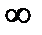
B) 1
C) 0
D) 3
E) 
F) 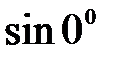
G) 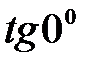
H) 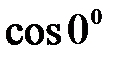
{Правильный ответ}=C, F, H
$$$007
 равен:
равен:
A) 0
B) 2004
C) 204
D) 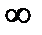
E) 1
F)ln1
G)lne
H)sin0
{Правильный ответ}=A, F, H
$$$008
 равен:
равен:
A) 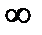
B) 0
C) 2
D) –2
E) 
F)ln1
G)lne
H)sin0
{Правильный ответ}=B, F,H
$$$009
 равен:
равен:
A) 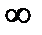
B) 1
C) 0
D) 3
E) 
F) ln1
G) lne
H) sin0
{Правильный ответ}=C, F, H
$$$001
Предел функции 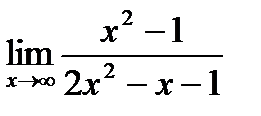 равен:
равен:
A) 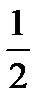
B) 3
C) -1
D) 0,5
E)
F) 1
G) 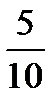
H) 0
{Правильный ответ} = A, D, G
$$$002
Предел функции 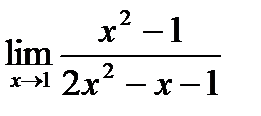 равен:
равен:
A) 1,5
B) 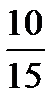
C) -1
D) 0,5
E) 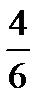
F) 1
G) 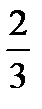
H) 0
{Правильный ответ} = B, E, G
$$$003
Предел функции  равен:
равен:
A) 
B) 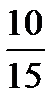
C) -1
D) 0,5
E) 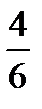
F) 1
G) 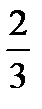
H) 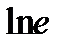
{Правильный ответ} = A, F, H
$$$004
Предел функции 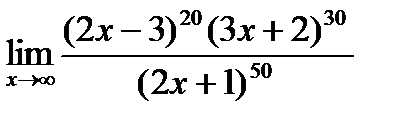 равен:
равен:
A) 
B) 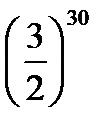
C) -1
D) 
E) 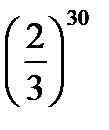
F) 1
G) 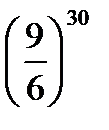
H) 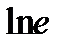
{Правильный ответ} = B, D, G
$$$005
Предел функции 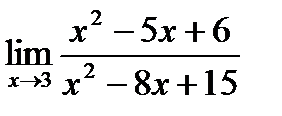 равен:
равен:
A) 
B) - 0,5
C) -1
D) 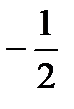
E) 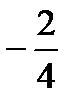
F) 1
G) 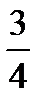
H) 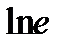
{Правильный ответ} = B, D, E
$$$006
Предел функции 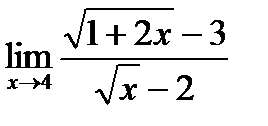 равен:
равен:
A) 
B) - 0,5
C) - 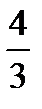
D) 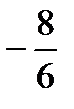
E) 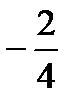
F) 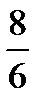
G) 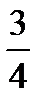
H) 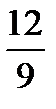
{Правильный ответ} = A, F, H
$$$007
Предел функции 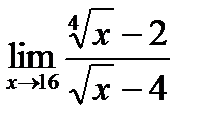 равен:
равен:
A) 
B) 0,25
C) - 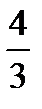
D) 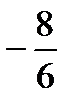
E) 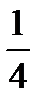
F) 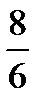
G) 
H) 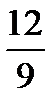
{Правильный ответ} = B, E, G
$$$008
Предел функции 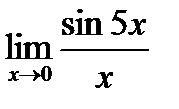 равен:
равен:
A) 5
B) -5
C) 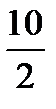
D) 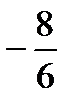
E) 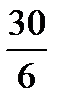
F) 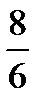
G) 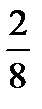
H) 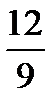
{Правильный ответ} = A, C,E
$$$009
Предел функции 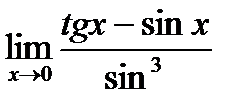 равен:
равен:
A) 
B) -5
C) 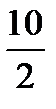
D) 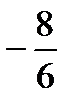
E) 
F) 
G) 0,5
H) 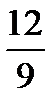
{Правильный ответ} = A, F,G
$$$010
Предел функции 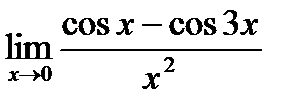 равен:
равен:
A) 
B) 4
C) 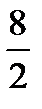
D) 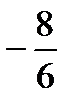
E) 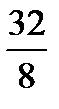
F) 
G) 0,5
H) 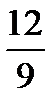
{Правильный ответ} = B, C,E
$$$011
Предел функции 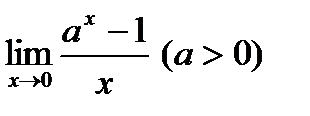 равен:
равен:
A) 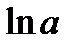
B) 4
C) 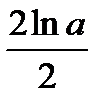
D) - 
E) 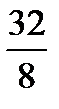
F) 
G) 0,5
H) 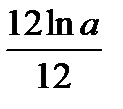
{Правильный ответ} = A, C,H
$$$012
Предел функции  равен:
равен:
A) 1
B) 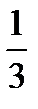
C) 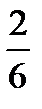
D) -1
E) 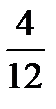
F) 
G) 0
H) 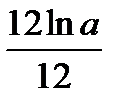
{Правильный ответ} = B, C,E
$$$013
Предел функции 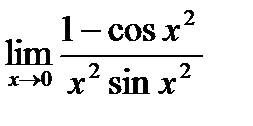 равен:
равен:
A) 1
B) 
C) 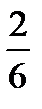
D) -1
E) 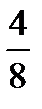
F) 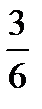
G) 0
H) 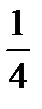
{Правильный ответ} = B,E,F
$$$014
Предел функции 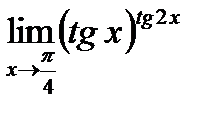 равен:
равен:
A) 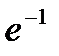
B) 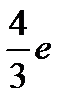
C) 
D) 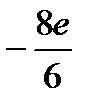
E) 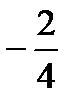
F) 
G) 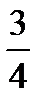
H) 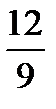
{Правильный ответ} = A, C, F
$$$015
Предел функции 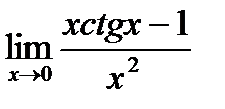 равен:
равен:
A) - 
B) 4
C) 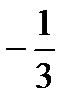
D) 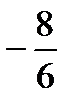
E) 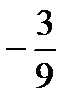
F) 
G) 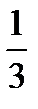
H) 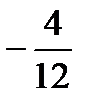
{Правильный ответ} = C, E, H
$$$016
Значение 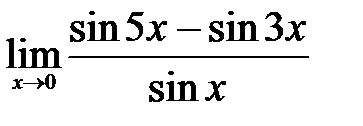 входит в промежуток:
входит в промежуток:
A) 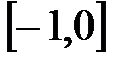
B) 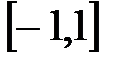
C) 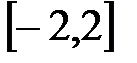
D) 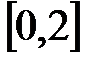
E) 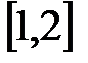
F) 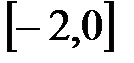
G) 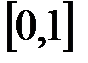
H) 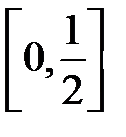
{Правильный ответ} = C, D, E
$$$017
Предел функции 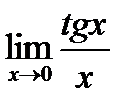 равен:
равен:
A) 
B) 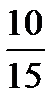
C) -1
D) 0,5
E) 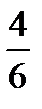
F) 1
G) 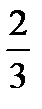
H) 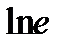
{Правильный ответ} = A, F, H
$$$018
Предел функции  равен:
равен:
A) 
B) 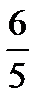
C) -1
D) 1,2
E) 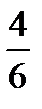
F) 1
G) 
H) 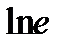
{Правильный ответ} = B, D, G
$$$019
Значение 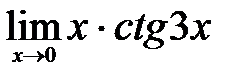 входит в промежуток:
входит в промежуток:
A) 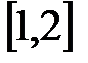
B) 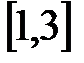
C) 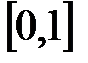
D) 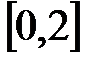
E) 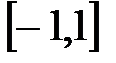
F) 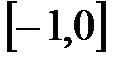
G) 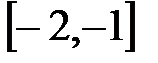
H) 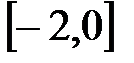
{Правильный ответ}=C, D, E
$$$020
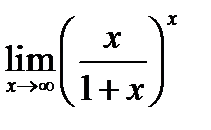 равен:
равен:
A) lne
B) е
C) 2lne
D)1
E) 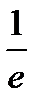
F) 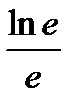
G) 
H) 4
{Правильный ответ}=E, F, G
$$$021
 равен:
равен:
A) lne
B) ln2
C) 3
D) 1
E) 4
F) sin0
G) 
H) -1
{Правильный ответ}=A, D, G
$$$022
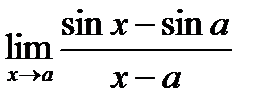 равен:
равен:
A) 
B) 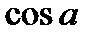
C) -1
D) 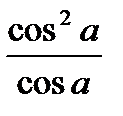
E) - 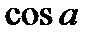
F) 1
G) 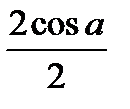
H) 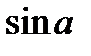
{Правильный ответ} = B, D,G
$$$023
Найти  :
:
A) 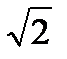
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|