- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Сложность
⇐ ПредыдущаяСтр 3 из 3
Сложность
| Есеп өлшемінің артуы барысында функцияның қозғалыс асимптотикасын қалай атайды A) динамикалық уақытша күрделілік B) статикалық уақытша күрделілік C) асимптотикалық уақытша күрделілік D) элементар уақытша күрделілік E) осы алгоритмнің уақытша күрделілігі | CE | Асимптотику поведения функции при увеличении размера задачи называют A) динамической временной сложностью B) статической временной сложностью C) асимптотичной временной сложностью D) элемеентарной временной сложностью E) временной сложностью этого алгоритма | ||||||||||||||||||||||||||||
| Орташа асимптотикалық уақыттық күрделілікті талдауды келесі типтерге бөлуге болады: A) динамикалық B) аналитикалық C) көптік D) статикалық E) сызықтық F) ортақтық | BD | Анализ средней асимптотической временной сложности можно разделить на следующие типы: A) динамический B) аналитический C) множественный D) статистический E) линейный F) массовый | ||||||||||||||||||||||||||||
| O(n) өсу ретіне қатысты дұрыс тұжырымдамалар A) кіріс массивінің артуымен байланысты алгоритм күрделілігі сызықты түрде артады B) есеп мөлшерін екі есе арттыру қажетті уақытты да екі есе арттырады C) кіріс массивінің өлшемінің артуымен байланысты алгоритм күрделілігі (орындалу уақыты) логарифмдік түрде артатынын білдіреді D) қойылған есепті екі еселеу қажетті уақытты төрт есеге арттырады E) қойылған есепті екі еселеу қажетті уақытты сегіз есеге арттырады F) алгоритмдерді талдауда үнсіздік бойынша он негіздегі логарифм алынады | AB | Правильные утверждение относительно порядка роста O(n) , A) сложность алгоритма линейно растет с увеличением входного массива B) удвоение размера задачи удвоит и необходимое время C) означает, что время выполнения алгоритма растет логарифмически с увеличением размера входного массива D) удвоение размера задачи увеличивает необходимое время в четыре раза E) удвоение размера задачи увеличивает необходимое время в восемь раз F) в анализе алгоритмов по умолчанию используется логарифм по основанию 10 | ||||||||||||||||||||||||||||
| O( log n) өсу ретіне қатысты дұрыс тұжырымдамалар A) кіріс массивінің артуымен байланысты алгоритм күрделілігі сызықты түрде артады B) қойылған есепті екі еселеу қажетті уақытты төрт есеге арттырады C) алгоритмдерді талдауда үнсіздік бойынша екі негіздегі логарифм алынады D) кіріс массивінің өлшемінің артуымен байланысты алгоритм күрделілігі (орындалу уақыты) логарифмдік түрде артатынын білдіреді E) алгоритмдерді талдауда үнсіздік бойынша он негіздегі логарифм алынады F) қойылған есепті екі еселеу қажетті уақытты сегіз есеге арттырады | CD | Правильные утверждение относительно порядка роста O( log n) A) сложность алгоритма линейно растет с увеличением входного массива B) удвоение размера задачи увеличивает необходимое время в четыре раза C) в анализе алгоритмов по умолчанию используется логарифм по основанию 2 D) означает, что время выполнения алгоритма растет логарифмически с увеличением размера входного массива E) в анализе алгоритмов по умолчанию используется логарифм по основанию 10 F) удвоение размера задачи увеличивает необходимое время в восемь раза | ||||||||||||||||||||||||||||
Функцияның асимптотикалық тәртібін салыстыру үшін белгілеу интерпретациялары:
A) 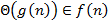  - ке жоғарыдан және төменнен - ке жоғарыдан және төменнен  функциясымен асимптотикалық түрде шектелген
B) функциясымен асимптотикалық түрде шектелген
B) 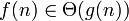 - -  , ,  - ға асимптотикалық эквивалентті
C) - ға асимптотикалық эквивалентті
C) 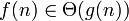 - -  - ке жоғарыдан және төменнен - ке жоғарыдан және төменнен  функциясымен асимптотикалық түрде шектелген
D) функциясымен асимптотикалық түрде шектелген
D)  - -  жоғарыдан жоғарыдан  (тұрақты көпмүшеге дейінгі нақтылықпен) функциясымен асимптотикалық түрде шектелген;
E) (тұрақты көпмүшеге дейінгі нақтылықпен) функциясымен асимптотикалық түрде шектелген;
E)  - -  , ,  - ға асимптотикалық эквивалентті
F) - ға асимптотикалық эквивалентті
F)  - -  жоғарыдан жоғарыдан  (тұрақты көпмүшеге дейінгі нақтылықпен) функциясымен асимптотикалық түрде шектелген;
G) (тұрақты көпмүшеге дейінгі нақтылықпен) функциясымен асимптотикалық түрде шектелген;
G) 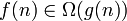 - -  , ,  - ға жоғарыдан - ға жоғарыдан  (тұрақты көпмүшеге дейінгі нақтылықпен) функциясымен асимптотикалық түрде шектелген (тұрақты көпмүшеге дейінгі нақтылықпен) функциясымен асимптотикалық түрде шектелген
| CD | Интерпретации обозначений для сравнения асимптотического поведения функций
A) 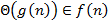  - ограничена снизу и сверху функцией - ограничена снизу и сверху функцией  асимптотически
B) асимптотически
B) 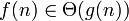 - -  эквивалентна эквивалентна  асимптотически
C) асимптотически
C) 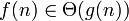 - -  ограничена снизу и сверху функцией ограничена снизу и сверху функцией  асимптотически
D) асимптотически
D)  - -  ограничена сверху функцией ограничена сверху функцией  (с точностью до постоянного множителя) асимптотически
E) (с точностью до постоянного множителя) асимптотически
E)  - -  эквивалентна эквивалентна  асимптотически
F) асимптотически
F)  - -  ограничена сверху функцией ограничена сверху функцией  (с точностью до постоянного множителя) асимптотически
G) (с точностью до постоянного множителя) асимптотически
G) 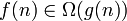 - -  ограничена сверху функцией ограничена сверху функцией  (с точностью до постоянного множителя) асимптотически (с точностью до постоянного множителя) асимптотически
| ||||||||||||||||||||||||||||
Функцияның асимптотикалық тәртібін салыстыру үшін белгілеу интерпретациялары:
A) 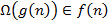 - -  төменнен төменнен  (тұрақты көпмүшеге дейінгі нақтылықпен) функциясымен асимптотикалық түрде шектелген;
B) (тұрақты көпмүшеге дейінгі нақтылықпен) функциясымен асимптотикалық түрде шектелген;
B) 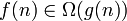 - -  , ,  - ға асимптотикалық эквивалентті
C) - ға асимптотикалық эквивалентті
C) 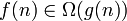 - -  төменнен төменнен  (тұрақты көпмүшеге дейінгі нақтылықпен) функциясымен асимптотикалық түрде шектелген;
D) (тұрақты көпмүшеге дейінгі нақтылықпен) функциясымен асимптотикалық түрде шектелген;
D) 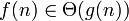 - -  , ,  - ға асимптотикалық эквивалентті
E) - ға асимптотикалық эквивалентті
E) 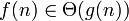 - -  - ке жоғарыдан және төменнен - ке жоғарыдан және төменнен  функциясымен асимптотикалық түрде шектелген
F) функциясымен асимптотикалық түрде шектелген
F) 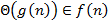  - ке жоғарыдан және төменнен - ке жоғарыдан және төменнен  функциясымен асимптотикалық түрде шектелген
G) функциясымен асимптотикалық түрде шектелген
G) 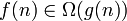 - -  , ,  - ға жоғарыдан - ға жоғарыдан  (тұрақты көпмүшеге дейінгі нақтылықпен) функциясымен асимптотикалық түрде шектелген; (тұрақты көпмүшеге дейінгі нақтылықпен) функциясымен асимптотикалық түрде шектелген;
| CE | Интерпретации обозначений для сравнения асимптотического поведения функций
A) 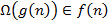 - -  ограничена снизу функцией ограничена снизу функцией  (с точностью до постоянного множителя) асимптотически
B) (с точностью до постоянного множителя) асимптотически
B) 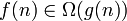 - -  эквивалентна эквивалентна  асимптотически
C) асимптотически
C) 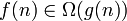 - -  ограничена снизу функцией ограничена снизу функцией  (с точностью до постоянного множителя) асимптотически
D) (с точностью до постоянного множителя) асимптотически
D) 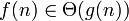 - -  эквивалентна эквивалентна  асимптотически
E) асимптотически
E) 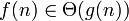 - -  ограничена снизу и сверху функцией ограничена снизу и сверху функцией  асимптотически
F) асимптотически
F) 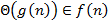 – –  ограничена снизу и сверху функцией ограничена снизу и сверху функцией  асимптотически
G) асимптотически
G) 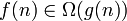 - -  ограничена сверху функцией ограничена сверху функцией  (с точностью до постоянного множителя) асимптотически (с точностью до постоянного множителя) асимптотически
| ||||||||||||||||||||||||||||
Алгоритмдер күрделілігінің асимптотикалық бағалануының дұрыс интерпретациясы:
A)  B)
B) 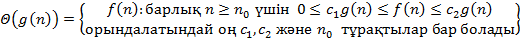 C)
C)  D)
D) 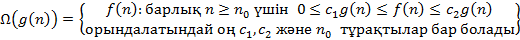 E)
E) 
| AB | Корректная интерпретация асимптотической оценки сложности алгоритмов:
A)  B)
B) 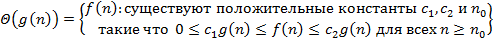 C)
C) 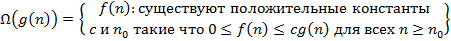 D)
D) 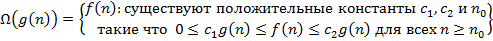 E)
E) 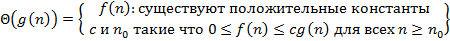
| ||||||||||||||||||||||||||||
Алгоритмдер күрделілігінің асимптотикалық бағалануының дұрыс интерпретациясы:
A) 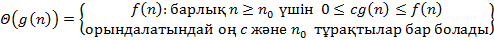 B)
B) 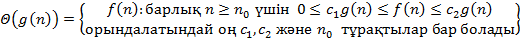 C)
C)  D)
D) 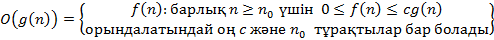 E)
E) 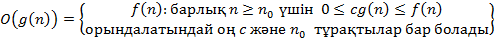
| BD | Корректная интерпретация асимптотической оценки сложности алгоритмов:
A) 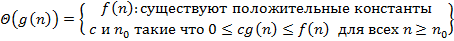 B)
B) 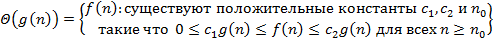 C)
C)  D)
D) 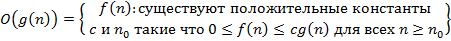 E)
E) 
| ||||||||||||||||||||||||||||
Алгоритмдер күрделілігінің асимптотикалық бағалануының дұрыс интерпретациясы:
A) 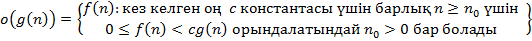 B)
B)  C)
C)  D)
D) 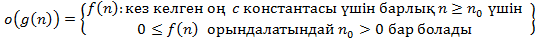 E)
E) 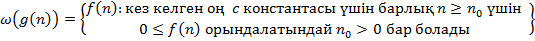 F)
F) 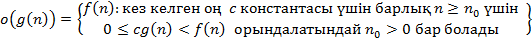
| AB | Корректная интерпретация асимптотической оценки сложности алгоритмов:
A) 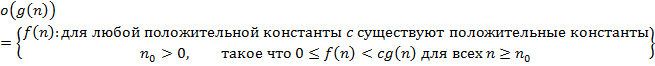 B)
B)  C)
C) 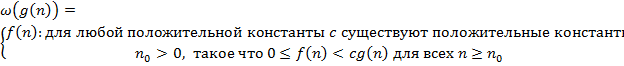 D)
D) 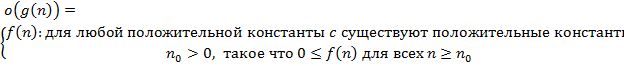 E)
E) 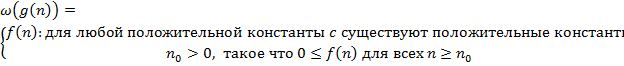 F)
F) 
| ||||||||||||||||||||||||||||
| Келесі сұрыптау алгоритмдері үшін максимальды және орташа уақыттық күрделілік O(n2) сәйкес: A) жедел Хоара сұрыптауы B) таңдау сұрыптауы, қарапайым енгізу сұрыптауы C) Шелл сұрыптауы D) Факториал сұрыптау E) көпіршік әдісімен сұрыптау F) біріктіру сұрыптауы, разряд бойынша сұрыптау G) таңдау сұрыптауы, Шелл сұрыптауы | BE | Для следующих алгоритмов сортировок соответствует максимальная и средняя временная сложность O(n2) A) быстрая сортировка Хоара B) сортировка выбором, сортировка простой вставкой C) сортировка Шелла D) факториальная сортировка E) сортировка пузырьком F) сортировка слиянием, поразряднаясортировка G)сортировка выбором, сортировка Шелла | ||||||||||||||||||||||||||||
| Алгоритмдердің күрделілігінің асимптотикалық талдауында грек әріптерінің белгіленуі A) Ο – күрделіліктің жоғарғы бағасы B) Ω – күрделіліктің жоғарғы бағасы C) Θ –күрделіліктің жоғарғы бағасы D) Ω – күрделіліктің нақты бағасы E) Θ – күрделіліктің нақты бағасы | AE | Использование греческих букв в асимптотическом анализе сложности алгоритмов: A) Ο – верхняя оценка сложности B) Ω – верхняя оценка сложности C) Θ – верхняя оценка сложности D) Ω – точная оценка сложности E) Θ – точная оценка сложности | ||||||||||||||||||||||||||||
| Алгоритмдердің күрделілігінің асимптотикалық талдауында грек әріптерінің белгіленуі: A) Ο – күрделіліктің төменгі бағасы B) Ω – күрделіліктің төменгі бағасы C) Θ – күрделіліктің нақты бағасы D) Ο –күрделіліктің нақты бағасы E) Ω – күрделіліктің нақты бағасы F) Θ – күрделіліктің төменгі бағасы G) Θ – күрделіліктің жоғарғы бағасы | BC | Использование греческих букв в асимптотическом анализе сложности алгоритмов: A) Ο – нижняя оценка сложности B) Ω – нижняя оценка сложности C) Θ – точная оценка сложности D) Ο – точная оценка сложности E) Ω – точная оценка сложности F) Θ – нижняя оценка сложности G) Θ –верхняя оценка сложности | ||||||||||||||||||||||||||||
| Алгоритмдер күрделілігінің асимптотикалық бағасы Ω, Θ, Ο мен a және b сандарының арасындағы қатынастар үшін келесі пареллельдерді жүргізуге болады: A) f(n) = Ω (g(n)) ≈ a≤b B) f(n) = Ο(g(n)) ≈ a ≤ b, f(n) = Θ(g(n)) ≈ a = b C) f(n) = Ω (g(n)) ≈ a=b, f(n) = Θ (g(n)) ≈ a ≥ b D) f(n) = Ο (g(n)) ≈ a ≥ b, f(n) = Ω (g(n)) ≈ a ≥ b E) f(n) = Ω (g(n)) ≈ a ≥ b | BE | Можно провести следующие параллели для отношений между асимптотическими оценками Ω, Θ, Ο сложности алгоритмов и числами а и b A) f(n) = Ω (g(n)) ≈ a≤b B) f(n) = Ο(g(n)) ≈ a ≤ b, f(n) = Θ(g(n)) ≈ a = b C) f(n) = Ω (g(n)) ≈ a=b, f(n) = Θ (g(n)) ≈ a ≥ b D) f(n) = Ο (g(n)) ≈ a ≥ b, f(n) = Ω (g(n)) ≈ a ≥ b E) f(n) = Ω (g(n)) ≈ a ≥ b | ||||||||||||||||||||||||||||
| Алгоритмдер күрделілігінің асимптотикалық бағасы Ω, Θ, Ο мен a және b сандарының арасындағы қатынастар үшін келесі пареллельдерді жүргізуге болады: A) f(n) = Ο (g(n)) ≈ a ≥ b, f(n) = Ω (g(n)) ≈ a ≥ b B) f(n) = Ο(g(n)) ≈ a ≤ b C) f(n) = Ω (g(n)) ≈ a ≥ b D) f(n) = Ω (g(n)) ≈ a=b, E) f(n) = Θ(g(n)) ≈ a = b F) f(n) = Θ (g(n)) ≈ a ≥ b | BC | Можно провести следующие параллели для отношений между асимптотическими оценками Ω, Θ, Ο сложности алгоритмов и числами а и b A) f(n) = Ο (g(n)) ≈ a ≥ b, f(n) = Ω (g(n)) ≈ a ≥ b B) f(n) = Ο(g(n)) ≈ a ≤ b C) f(n) = Ω (g(n)) ≈ a ≥ b D) f(n) = Ω (g(n)) ≈ a=b, E) f(n) = Θ(g(n)) ≈ a = b F) f(n) = Θ (g(n)) ≈ a ≥ b | ||||||||||||||||||||||||||||
Алгоритмдер күрделілігінің асимптотикалық бағасы 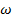 , ο мен a және b сандарының арасындағы қатынастар үшін келесі пареллельдерді жүргізуге болады:
A) f(n) = ο (g(n)) ≈ a ≥ b,
B) f(n) = ο(g(n)) ≈ a < b
C) f(n) = , ο мен a және b сандарының арасындағы қатынастар үшін келесі пареллельдерді жүргізуге болады:
A) f(n) = ο (g(n)) ≈ a ≥ b,
B) f(n) = ο(g(n)) ≈ a < b
C) f(n) = 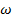 (g(n)) ≈ a > b
D) f(n) = (g(n)) ≈ a > b
D) f(n) = 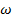 (g(n)) ≈ a=b,
E) f(n) = (g(n)) ≈ a=b,
E) f(n) = 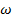 (g(n)) ≈ a ≥ b
F)f(n) = (g(n)) ≈ a ≥ b
F)f(n) =  (g(n)) ≈ a = b
G) f(n) = o (g(n)) ≈ a (g(n)) ≈ a = b
G) f(n) = o (g(n)) ≈ a 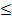 b b
| BC | Можно провести следующие параллели для отношений между асимптотическими оценками 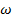 , ο сложности алгоритмов и числами а и b
A) f(n) = ο (g(n)) ≈ a ≥ b,
B) f(n) = ο(g(n)) ≈ a < b
C) f(n) = , ο сложности алгоритмов и числами а и b
A) f(n) = ο (g(n)) ≈ a ≥ b,
B) f(n) = ο(g(n)) ≈ a < b
C) f(n) = 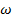 (g(n)) ≈ a > b
D) f(n) = (g(n)) ≈ a > b
D) f(n) = 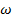 (g(n)) ≈ a=b,
E) f(n) = (g(n)) ≈ a=b,
E) f(n) = 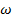 (g(n)) ≈ a ≥ b
F)f(n) = (g(n)) ≈ a ≥ b
F)f(n) =  (g(n)) ≈ a = b
G) f(n) = o (g(n)) ≈ a (g(n)) ≈ a = b
G) f(n) = o (g(n)) ≈ a 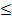 b b
| ||||||||||||||||||||||||||||
| Алгоритмдер күрделілігінің О-бағалануы үшін келесі арақатынастар шынайы: A) O(f/g) = O(f)*O(g), O(f*g) = O(f) + O(g), O(f+g) = O(f) *O(g) B) O(k*f)=k *O(f), O(f+g) = O(f) *O(g) C) O(f*g)=O(f) / O(g) D) O(k*f) = O(f), O(f*g) = O(f)*O(g), E) O(f*g) = O(f) + O(g), O(f+g) = O(f) *O(g) F) O(f+g), O(f) және O(g) доминантына тең | DF | Для О- оценки сложности алгоримов справедливы следующие соотношения A) O(f/g) = O(f)*O(g), O(f*g) = O(f) + O(g), O(f+g) = O(f) *O(g) B) O(k*f)=k *O(f), O(f+g) = O(f) *O(g) C) O(f*g)=O(f) / O(g) D) O(k*f) = O(f), O(f*g) = O(f)*O(g), E) O(f*g) = O(f) + O(g), O(f+g) = O(f) *O(g) F) O(f+g), равен доминанту O(f) и O(g) | ||||||||||||||||||||||||||||
| Алгоритмдер күрделілігінің О-бағалануы үшін келесі арақатынастар шынайы: A) O(k*f) = O(f) B) O(k*f)=k *O(f), O(f+g) = O(f) *O(g) C) O(f*g)=O(f) / O(g) D) O(f*g) = O(f)*O(g), O(f+g), O(f) және O(g) доминантына тең E) O(k*f)=k +O(f), O(f+g) = O(f) *O(g) F) O(f*g) = O(f) + O(g), O(f+g) = O(f) *O(g) G) O(f+g) = O(f) *O(g) O(f/g) = O(f)*O(g), O(f*g) = O(f) + O(g), | AD | Для О- оценки сложности алгоримов справедливы следующие соотношения A) O(k*f) = O(f) B) O(k*f)=k *O(f), O(f+g) = O(f) *O(g) C) O(f*g)=O(f) / O(g) D) O(f*g) = O(f)*O(g), O(f+g), равен доминанту O(f) и O(g) E) O(k*f)=k +O(f), O(f+g) = O(f) *O(g) F) O(f*g) = O(f) + O(g), O(f+g) = O(f) *O(g) G) O(f+g) = O(f) *O(g) O(f/g) = O(f)*O(g), O(f*g) = O(f) + O(g), | ||||||||||||||||||||||||||||
| Алгоритмдер күрделілігінің О-бағалануы үшін келесі арақатынастар шынайы: A) O(f*g) = O(f)*O(g) B) O(k*f)=k *O(f), O(f+g) = O(f) *O(g) C) O(f*g)=O(f) / O(g) D) O(k*f) = O(f), , O(f+g), O(f) және O(g) доминантына тең E) O(f/g) = O(f)*O(g), O(f*g) = O(f) + O(g), O(f+g) = O(f) *O(g) | AD | Для О- оценки сложности алгоримов справедливы следующие соотношения A) O(f*g) = O(f)*O(g) B) O(k*f)=k *O(f), O(f+g) = O(f) *O(g) C) O(f*g)=O(f) / O(g) D) O(k*f) = O(f), , O(f+g), ), равен доминанту O(f) и O(g) E) O(f/g) = O(f)*O(g), O(f*g) = O(f) + O(g), O(f+g) = O(f) *O(g) | ||||||||||||||||||||||||||||
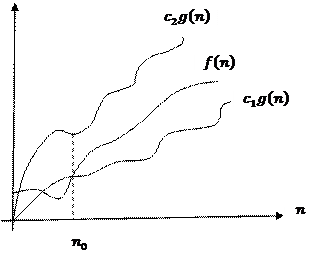
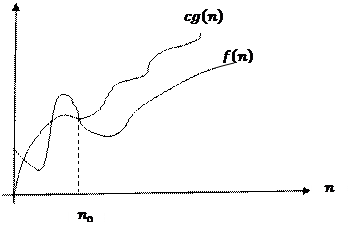
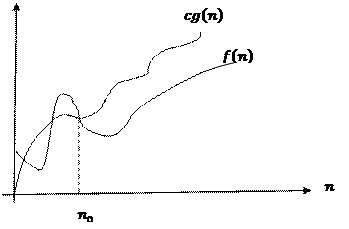
Асимптотикалық бағалау графиктерінің дұрыс сәйкестіктері:
A)
B)
C)
D)
E)
F)
G) | AD | Правильное соответствие графика асимптотической оценке
A)
B)
C)
D)
E)
F)
G) | ||||||||||||||||||||||||||||
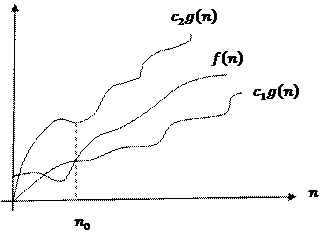
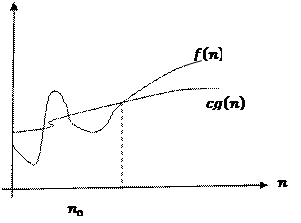
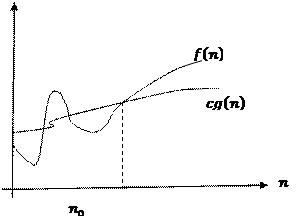
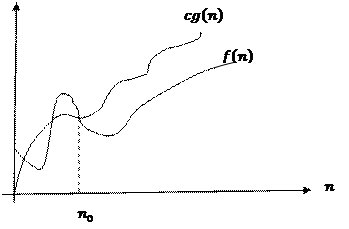
Асимптотикалық бағалау графиктерінің дұрыс сәйкестіктері:
A)
B)
C)
D)
E)
F) G) | BC | Правильное соответствие графика асимптотической оценке
A)
B)
C)
D)
E)
F) G) | ||||||||||||||||||||||||||||
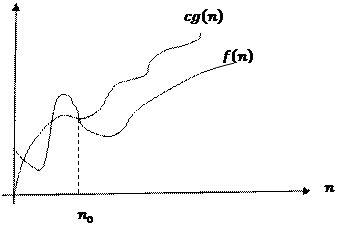
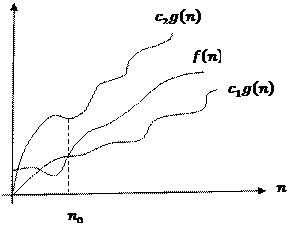
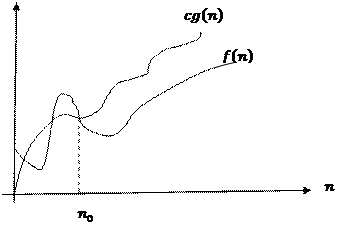
Асимптотикалық бағалау графиктерінің дұрыс сәйкестіктері:
A)
B)
C)
D)
E)
F)
G) | CF | Правильное соответствие графика асимптотической оценке
A)
B)
C)
D)
E)
F)
G) | ||||||||||||||||||||||||||||
Алгоритмдер күрделілігінің асимптотикалық бағалануының дұрыс интерпретациясы:
A) 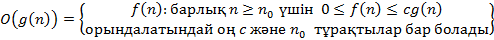 B)
B) 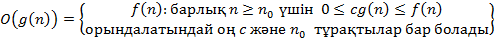 C)
C)  D)
D) 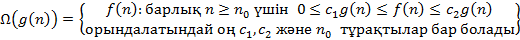 E)
E) 
| AE | Корректная интерпретация асимптотической оценки сложности алгоритмов:
A) 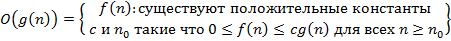 B)
B)  C)
C) 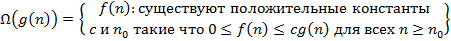 D)
D) 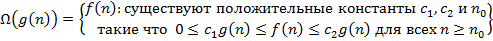 E)
E) 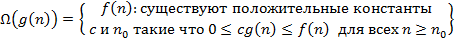
| ||||||||||||||||||||||||||||
| Алгоритмдер күрделілігінің асимптотикалық бағасы Ω, Θ, Ο мен a және b сандарының арасындағы қатынастар үшін келесі пареллельдерді жүргізуге болады: A) f(n) = Ω (g(n)) ≈ a≤b B) f(n) = Ο(g(n)) ≈ a ≤ b, f(n) = Ω (g(n)) ≈ a ≥ b C) f (n) = Θ (g(n)) ≈ a ≤ b, f(n) = Ω (g(n)) ≈ a ≤ b D) f(n) = Ω (g(n)) ≈ a=b, f(n) = Θ (g(n)) ≈ a ≥ b E) f(n) = Ο (g(n)) ≈ a ≥ b, f(n) = Ω (g(n)) ≈ a ≥ b F) f(n) = Θ (g(n)) ≈ a = b G) f(n) = Θ (g(n)) ≈ a ≤ b, f(n) = Ω (g(n)) ≈ a ≥ b | BF | Можно провести следующие параллели для отношений между асимптотическими оценками Ω, Θ, Ο сложности алгоритмов и числами а и b A) f(n) = Ω (g(n)) ≈ a≤b B) f(n) = Ο(g(n)) ≈ a ≤ b, f(n) = Ω (g(n)) ≈ a ≥ b C) f (n) = Θ (g(n)) ≈ a ≤ b, f(n) = Ω (g(n)) ≈ a ≤ b D) f(n) = Ω (g(n)) ≈ a=b, f(n) = Θ (g(n)) ≈ a ≥ b E) f(n) = Ο (g(n)) ≈ a ≥ b, f(n) = Ω (g(n)) ≈ a ≥ b F) f(n) = Θ (g(n)) ≈ a = b G) f(n) = Θ (g(n)) ≈ a ≤ b, f(n) = Ω (g(n)) ≈ a ≥ b | ||||||||||||||||||||||||||||
| n элементтен тұратын массивтегі сызықты іздеу кезіндегі ең жақсы, ең жаман және орташа жағдайлардағы салыстырулар саны: A) log n B) n/2 және n2 C) 100000 D) n/3 E) n/2 және 1 F) n -1 және n+1 G) n | EG | Количество сравнений во время линейного поиска в массиве, состоящем из n элементов наилучших, наихудших и средних случаев A) logn B) n/2 иn2 C) 100000 D) n/3 E) n/2 и1 F) n -1и n+1 G) n |
ФИКС
| (a+b)*c-d/(e-f) арифметикалық өрнегіне сәйкес постфиксті және префиксті формаларын көрсетіңіз: A)ab+c*def-/- B) (a+b)*(c+d) C) a + b * c D) a * b + c * d E)-*+abc/d-ef F)(a+b)*c G)d/(e-f) | A) E) | Префиксная, постфиксная и инфиксная формы арифметического выражения(a+b)*c-d/(e-f) A)ab+c*def-/- B) (a+b)*(c+d) C) a + b * c D) a * b + c * d E)-*+abc/d-ef F)(a+b)*c G)d/(e-f) | |||
| (z+2)*(x+y) арифметикалық өрнегін префиксті жазбада көрсетіңіз: A) * + z 2 + x y B) * (+ (z 2) (+ x y)) C)(z+2)*(x+y) D)z 2 + x y + *. E)z 2* + x y + -. F)(z+2)*(x+y) G)z+2*x+y | A) B) | Арифметическое выражение (z+2)*(x+y) представьте в префиксной форме записи: A)* + z 2 + x y B)* (+ (z 2) (+ x y)) C)(z+2)*(x+y) D)z 2 + x y + *. E)z 2* + x y + -. F)(z+2)*(x+y) G)z+2*x+y | |||
| Постфиксті жазба дегеніміз не? A) операция белгісі операндтан кейін қойылады. B) операция белгісі операндтың алдында қойылады C)операциябелгілеріоперандтарарасындаорналасқан. D) тек қанаоперандтарданжәнефункциялардантұрады E)есептеулер операция приоритетінесәйкесжүргізіледі. F)операция символы операндтарданкейінжазылады G)оператор операндтыңсолжағындаорналасады H) жазбалар болмайды және өрнекті есептеу ретін бірмәнді анықтайды | A) F) | Постфиксная запись – A)знак операции ставится после операндов. B) знак операции ставится перед операндами C)знак операции ставится между операндами. D)состоит только из операндов и функций E)вычисления проводятся в соответствии с приоритетом. F)символ операцииставится после операндов G)оператор ставится левее операнда H) записи не бывают и однозначно определяет порядок вычисления выражений | |||
| Префиксті жазбаның анықтамасы: A) операция белгілері операндтар арасында орналасқан B) есептеулер операция приоритетіне сәйкесжүргізіледі C) операция белгісі операндтың алдында қойылады D) операция белгісі операндтан кейін қойылады E) префикстік жазбада жазбалар болмайды және өрнекті есептеу ретін бірмәнді анықтайды F) тек қанаоперандтарданжәнефункциялардантұрады G)операция символы операндтардың алдындажазылады H)оператор операндтыңсолжағындаорналасады | C) G) | Префиксная запись – A) знак операции ставится между операндами. B) вычисления проводятся в соответствии с приоритетом. C)знак операции ставится перед операндом D)знак операции ставится после операндов. E) записей не бывает и однозначно определяет порядок вычисления выражений F)состоит только из операндов и функций G)символ операцииставится перед операндами H)оператор ставится левее операнда | |||
| Инфиксті жазба дегеніміз? A) операция белгісі операндтан кейін қойылады. B) тек қана операндтардан және функциялардан тұрады C) операция символы операндтарға дейінкейінжазылады D) операция белгісі операндтың алдында қойылады E)операция белгілеріоперандтарарасындаорналасқан F) оператор операндтыңсолжағындаорналасады G)есептеулер операция приоритетінесәйкесжүргізіледі | E) G) | Инфиксная запись – A) знак операции ставится после операндов. B) состоит только из операндов и функций C) знак операции ставится перед операндом D) знак операции ставится до операндов E)знак операции ставится между операндами F) оператор ставится левее операнда G)вычисления проводятся в соответствии с приоритетом. | |||
| Инфиксті өрнектің дұрыснұсқалары: A)A B C * + D + B)+ * A B * C D C)A * B + C * D D) A + B + C + D E)A B + C D + * F)A B * C D * + | C) D) | Правильные варианты ификсной записи A)A B C * + D + B)+ * A B * C D C)A * B + C * D D) A + B + C + D E)A B + C D + * F)A B * C D * + |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|