- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Міністерство освіти і науки, молоді та спорту України
Міністерство освіти і науки, молоді та спорту України
Харківська національна академія міського господарства
Інженерна графіка
Робочий зошит для підготовки до виконання лабораторних робіт (для студентів 1 курсу денної форми навчання за напрямом підготовки 6.060101 «Будівництво»)
Харків
ХНАМГ
Робочий зошит для підготовки до виконання лабораторних робіт з
курсу «Інженерна графіка» (для студентів 1 курсу денної форми навчання за напрямом підготовки 6.060101 «Будівництво»)/ Уклад. Т.Є. Киркач.-Харк. нац. акад.. міськ. госп-ва.- Х.: ХНАМГ, 2011.- 94 с.
Укладач: Т.Є Киркач
Рецензент: к.т.н. проф. В.І. Лусь
Рекомендовано кафедрою інженерної та комп’ютерної графіки, протокол №3 від 26.10.20011 р.
ПЕРЕДМОВА
Цей робочий зошит створено для полегшення конспектування лекцій, більш чіткої організації в проведенні практичних занять і економії часу при видачі нового матеріалу.
Розвинутий план за темами, наданий в робочому зошиті, охоплює і відображає структурну схему побудови курсу нарисної геометрії, що допоможе студенту під час самостійної роботи сформувати алгоритмічний підхід до вивчання матеріалу, швидше і простіше орієнтуватися при користуванні підручниками акцентувати увагу на основних питаннях.
До кожної з тем надані умови типових задач, розв’язування яких допоможе при підготовці до іспитів, і питання для самоперевірки.
Умовні позначення
Точки позначаються великими літерами латинського алфавіту, наприклад, А, В, С,……, а також цифрами 1, 2, 3,….
Лінії позначаються малими літерами латинського алфавіту, наприклад, a, b,….l, m, n, …..
Площини позначаються великими літерами грецького алфавіту, наприклад, Σ, Ω, Δ,….
Проекції точок, ліній та площин позначають такими самими літерами, що й оригінали, тільки з індексами, які відповідають індексам площин проекцій, наприклад, А1, А2, А3, ………, m1, m2, m3, ………, Σ1, Σ2, Σ3.
Графічні знаки – символи мають таке значення:
// - паралельність; Ì - належність;
Ç - перетин; (А Ì Σ - означає, що точка А
^ - перпендикулярність; належить площині Σ)
= - результат дії; É - включення;
º - суміщення; (Σ É А- означає, що площина Σ
 - символ мимобіжних прямих; включає точку А)
- символ мимобіжних прямих; включає точку А)
È - символ з’єднання;
1. МЕТОД ПРОЕКЦІЮВАННЯ
1.1. Центральне проекціювання.
1.2. Паралельне проекціювання. Основні властивості.
1.3. Розв’язування задач з теми «Метод проекціювання».
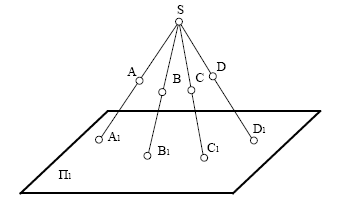
1.1. Центральне проекціювання
|
| Рис. 1.1 |
А, B,С, D- об'єкти проекціювання;
S - центр проекцій;
П1 - площина проекцій;
А1, В1, С1, D1- проекції точок на площині П1
1.2. Паралельне проекціювання. Основні властивості
1.3. Розв’язування задач з теми «Метод проекціювання».
Задача 1.1 Побудувати паралельні проекції заданих геометричних образів, прийнявши q за напрямок проекціювання.
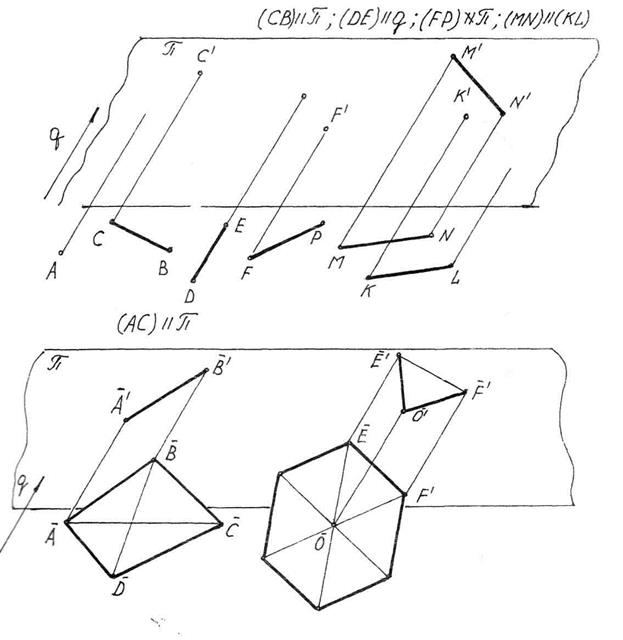
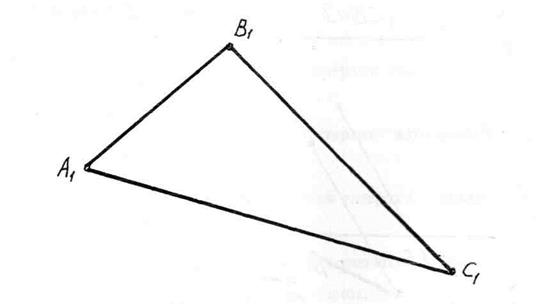
Задача 1.2. Трикутник А1В1С1 – паралельна проекція правильного трикутника. Побудувати проекцію правильного вписаного шестикутника, вибрав за діагоналі бісектриси кутів.
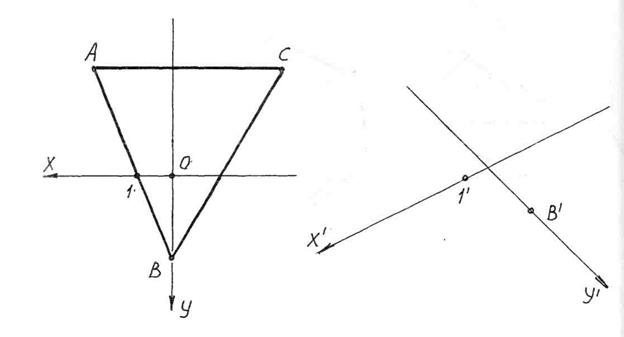
Задача 1.3. Побудувати паралельну проекцію ΔАВС (А¢ В¢ С¢), віднесеного до прямокутної системи координат XOY, якщо паралельна проекція системи координат і точок 1¢ та В¢ задані.
2. ПРОЕКЦІЇ ТОЧКИ
2.1. Точка в системі двох площин проекцій.
Епюр Монжа.
2.2. Точка в системі трьох площин проекцій.
2.3. Розв’язування задач по темі «Проекції точки».
2.1. Точка в системі двох площин проекцій. Епюр Монжа
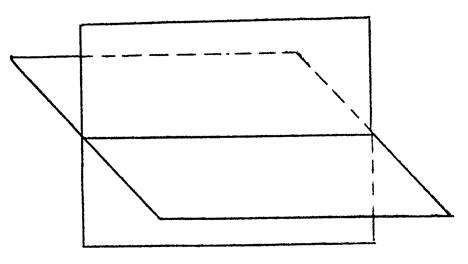
|
| Рис. 2.1 |
 |
2.2. Точка в системі трьох площин проекцій
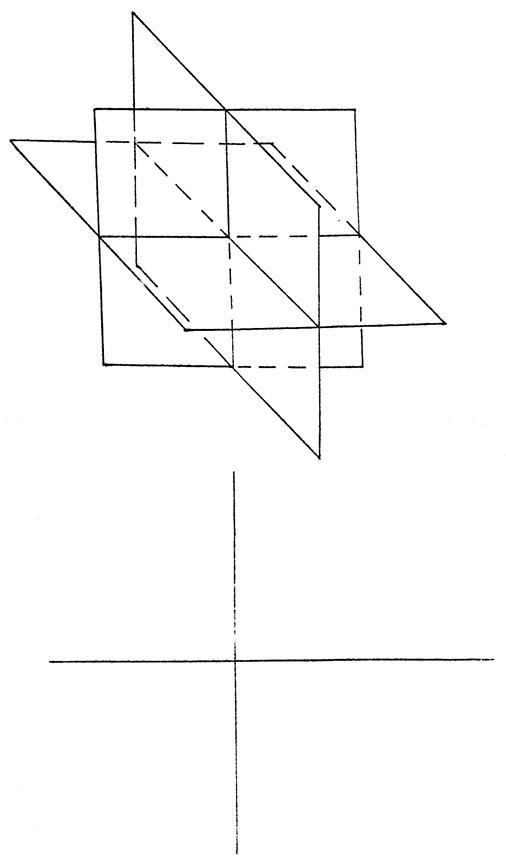
|
| Рис. 2.2 |
2.3. Розв’язування задач по темі «Проекції точки»
Задача 2.1. Побудувати двокартинний комплексний кресленик точок і визначити, в яких чвертях та площинах вони розташовані
| A | (25 ; 10 ; 30) | C | (10 ; 35 ; 45) |
| B | (35 ; 25 ; 60) | D | (45 ; 35 ; 20) |
| E | (55 ; 0 ;-30) | K | (80 ;-15 ; 50) |
| F | (65 ;-35 ; 15) | M | (105;-25 ;-10) |
| L | (95 ; 0 ; 0) | N | (120; -40; 0) |
| O | (130;-30 ;-15) | P | (135; 55 ;-20) |
| S | (85 ; 10 ;-30) |
 |
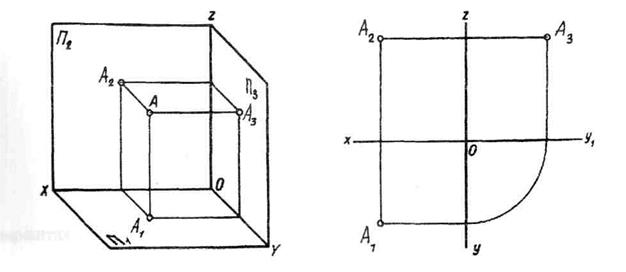
Задача 2.2 .По даним в табл.1 координатам побудувати наочне зображення точок А, В, С і D та епюри цих точок. Для побудови кожної точки виконати окреме креслення. При побудові наочного зображення, вісь OY проводити з точки О під кутом 45º до горизонталі; по осі OY відкладати половину заданого у таблиці розміру, по осям OX, OZ – натуральну величину. При побудові ортогональних проекцій точок по осям X,Y і Z від точки О відкладати натуральну величину координат, заданих у табл.1.
Таблиця 1
| № варіанта | А | В | С | D | ||||||||
| X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | |
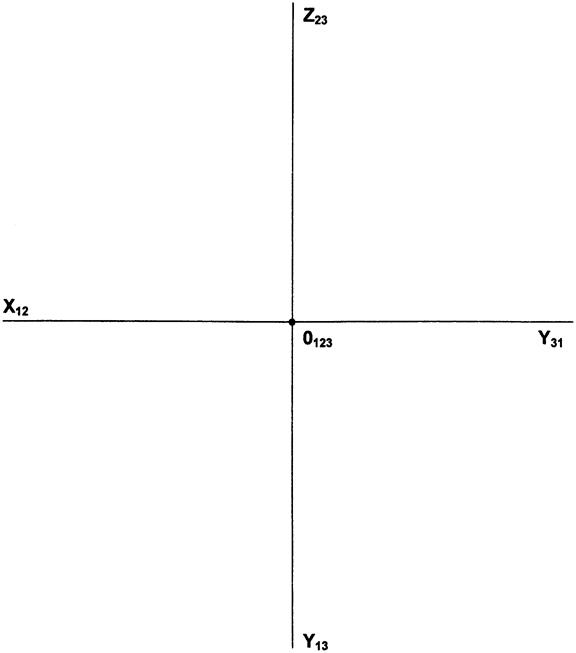
Задача 2.3. Побудувати на трикартинному КК точки і визначити в яких октантах простору вони розташовані
А (10; 30; 20)
В (20; 15; -40)
С (50; -15; 25)
D (-50; 20; 30)
Е (-40; 10; -50)
F (30; -25; -10)
G (-60; -30; 40)
3. ЗАДАННЯ ПРЯМОЇ НА КРЕСЛЕНИКУ
3.1. Класифікація прямих та побудова їх проекцій.
3.1.1. Комплексний кресленик прямої довільного положення.
3.1.2. Прямі особливого положення.
3.2. Взаємне положення прямої і точки.
3.3. Взаємне положення двох прямих.
3.3.1. Теорема про проекціювання прямого кута.
3.4. Сліди прямої.
3.5. Справжня величина відрізка прямої та кути нахилу її до площин проекцій.
3.6. Розв’язування задач по темі «Задання прямої на кресленику».
3.1. Класифікація прямих та побудова їх проекцій
3.1.1. Комплексний кресленик прямої довільного положення
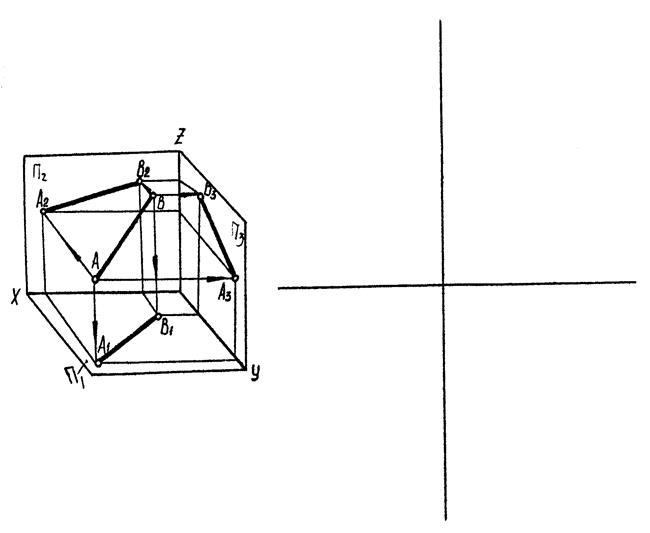
|
| Рис. 3.1 |
3.1.2. Прямі особливого положення
Лінії рівня
А)
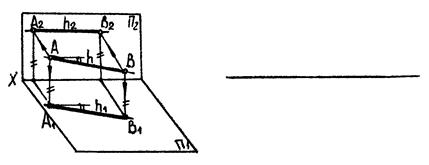
|
| Рис. 3.2 |
Б)
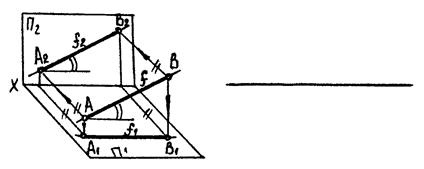
|
| Рис. 3.3 |
В)
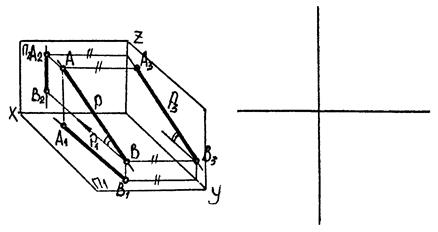
|
| Рис. 3.4 |
Проекційні прямі
А)
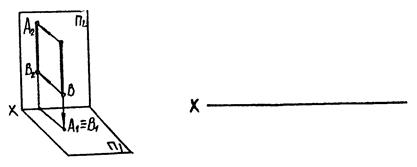
|
| Рис. 3.5 |
Б)
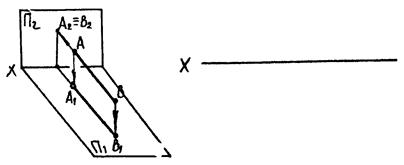
|
| Рис. 3.6 |
В)
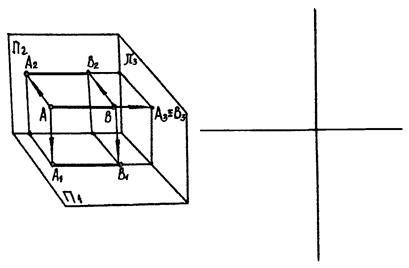
|
| Рис. 3.7 |
3.2. Взаємне положення прямої і точки
3.3. Взаємне положення двох прямих
А)

|
| Рис. 3.8 |
Б)

|
| Рис. 3.9 |
В)

|
| Рис. 3.10 |
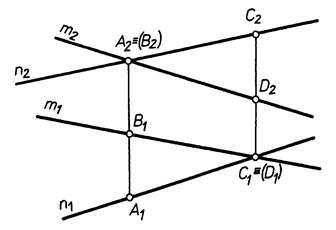
|
| Рис. 3.11 |
3.3.1 .Теорема про проекціювання прямого кута
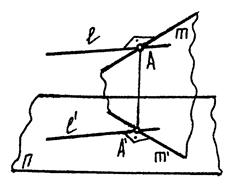
|
| Рис. 3.12 |
3.4. Сліди прямої
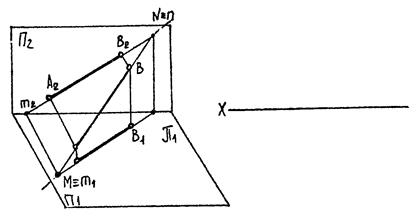
|
| Рис. 3.13 |
3.5. Справжня величина відрізка прямої лінії та кути нахилу її до площин проекцій
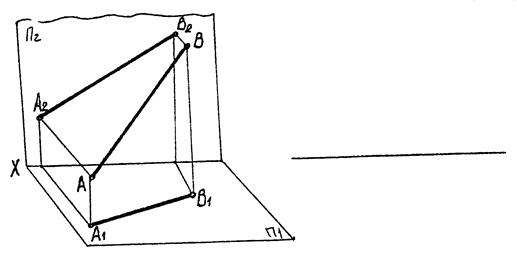
|
| Рис. 3.14 |
3.6. Розв’язування задач по темі «Задання прямої на кресленику»
Задача 3.1 Методом прямокутного трикутника визначити дійсну довжину відрізків прямих та кути їх нахилу до площин проекцій П1 та П2.
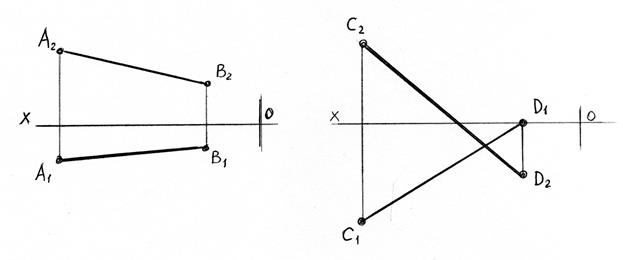
Задача 3.2. Побудувати сліди прямих на кресленні та визначити, крізь які чверті простору проходять ці прямі.
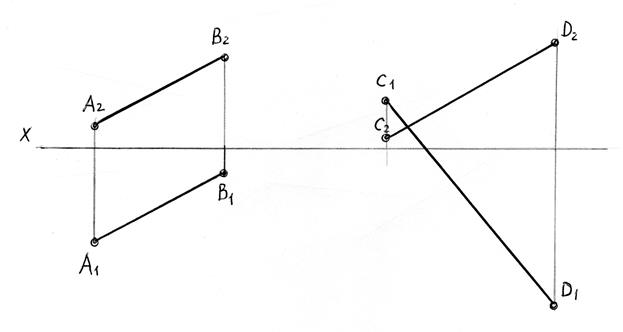
Задача 3.3. Визначити відстань від точки А до заданої прямої.
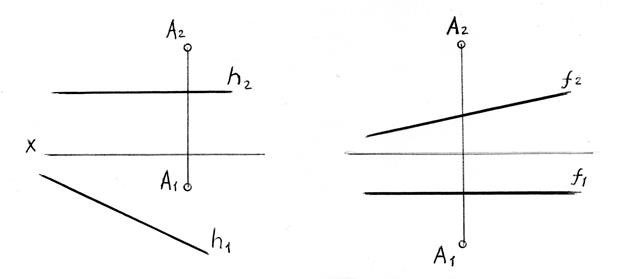
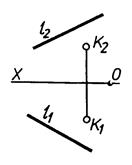
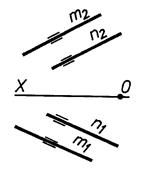
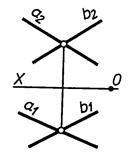
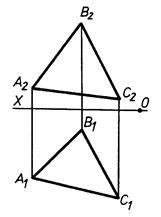
Задача 3.3 Визначити взаємне положення прямих (АВ) і (CD). Для випадку «в» знайти конкуруючі точки
а) б)
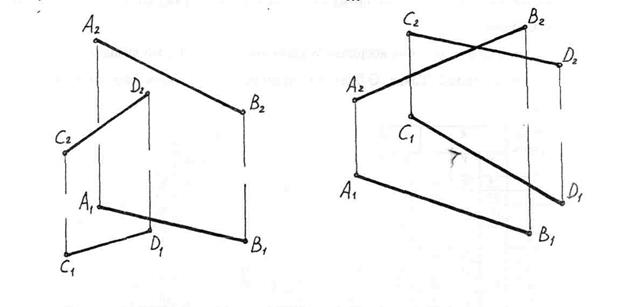
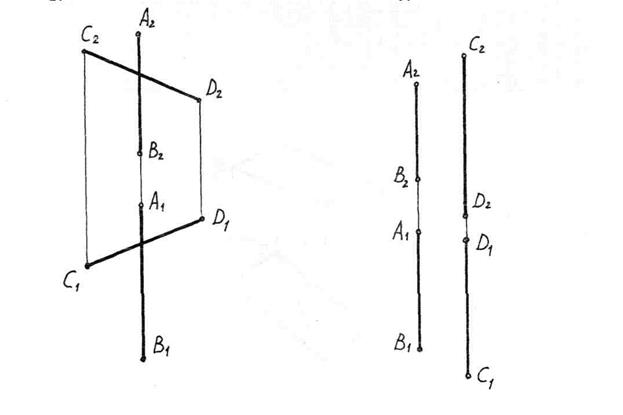
в) г)
4. ЗОБРАЖЕННЯ ПЛОЩИНИ
4.1. Способи задання площини на кресленику.
4.2. Класифікація площин.
4.2.1. Площини рівня.
4.2.2. Проекційні площини.
4.3. Пряма та точка в площині.
4.4. Прямі особливого положення в площині.
4.5. Розв’язування задач по темі «Зображення площини».
4.1. Способи задання площини на кресленику
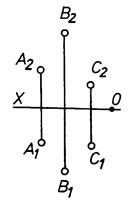
|
|
| |||
| Рис. 4.1 | Рис. 4.2 | Рис. 4.3 | |||
|
|
| ||||
| Рис 4.4 | Рис. 4.5 | ||||
|
|
| ||||
| Рис. 4.6
|
| ||||
4.2. Класифікація площин
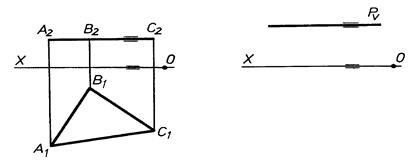
4.2.1. Площини рівня
А)
|
| Рис. 4.7 |
Б)
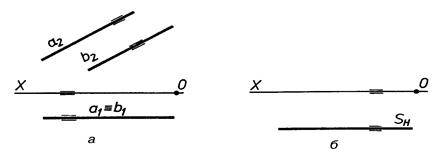
|
| Рис. 4.8 |
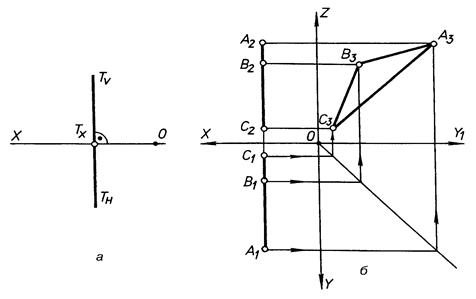
В)
|
| Рис. 4.9 |
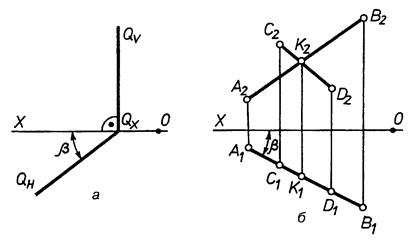
4.2.2. Проекційні площини
А)
|
| Рис. 4.10 |
Б)
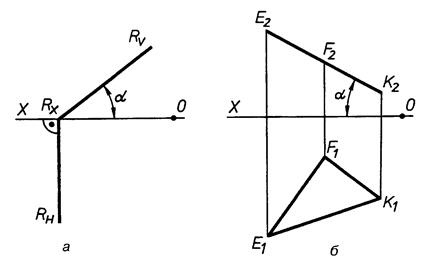
|
| Рис. 4.11 |
В)
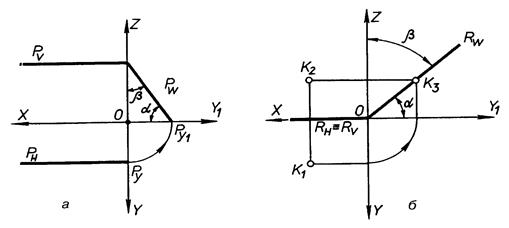
|
| Рис. 4.12 |
4.3. Пряма та точка в площині
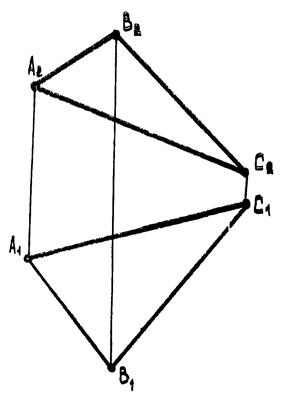
|
| Рис. 4.13 |
4.4. Прямі особливого положення в площині
А)
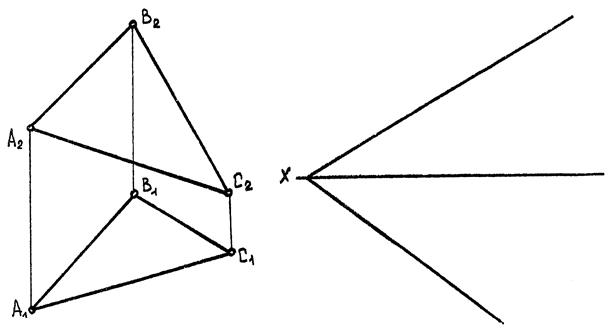
|
| Рис. 4.14 |
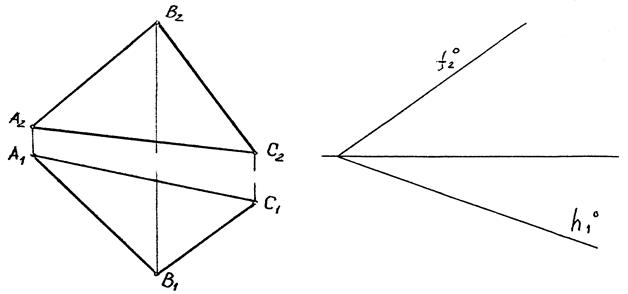
Б)
|
| Рис. 4.15 |
В)
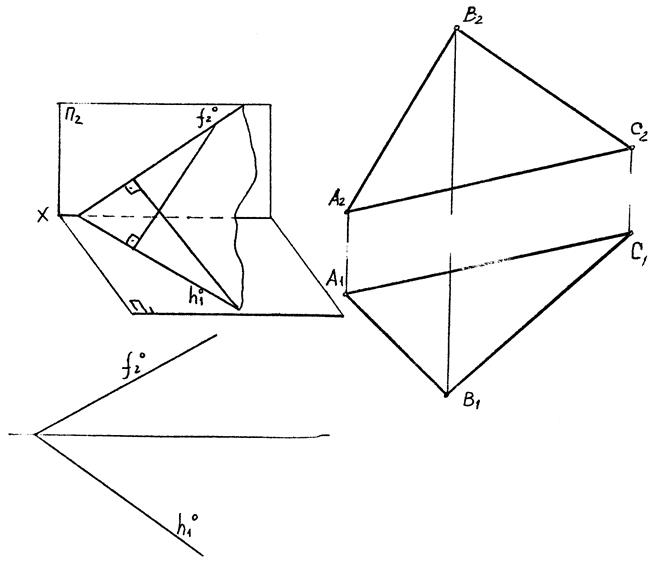
|
| Рис. 4.16 |
4.5. Розв’язування задач по темі «Зображення площини»
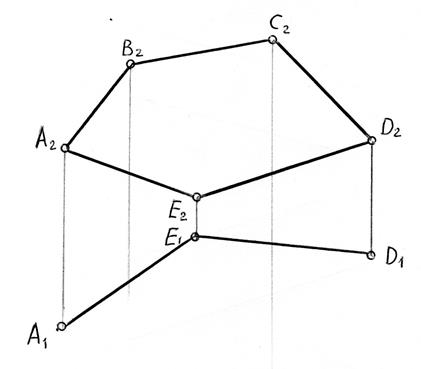
Задача 4.1. Побудувати горизонтальну проекцію плоского п’ятикутника ABCDE за його фронтальною проекцією та горизонтальною проекцією двох суміжних сторін. Визначити кут нахилу площини до однієї з площин проекцій ( П1 чи П2).
Задача 4.2 . Задано фронтальну проекцію ∆АВС, що лежить в площині Q. Побудувати невистачаючу проекцію ∆АВС:
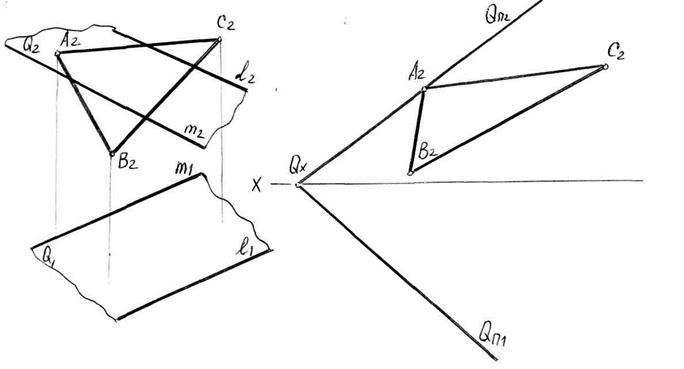
а) площина Q задана прямими ℓ║ m, б) площина Q задана слідами.
Задача 4.3. В площині ΔАВС провести лінії рівня через точку К. Визначити кут нахилу площини Δ АВС до площини П2.
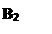
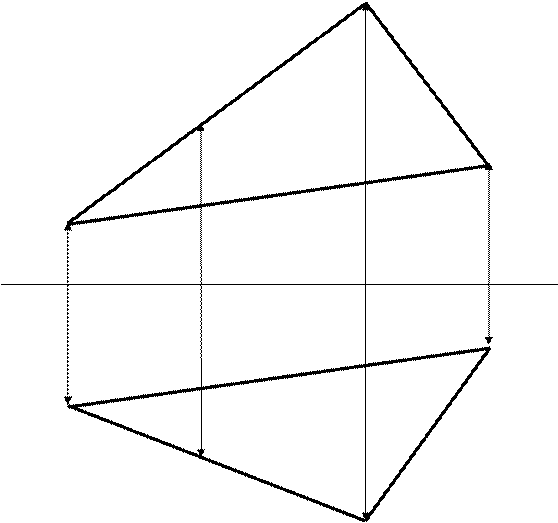 |
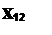
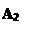
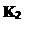
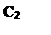
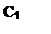
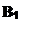
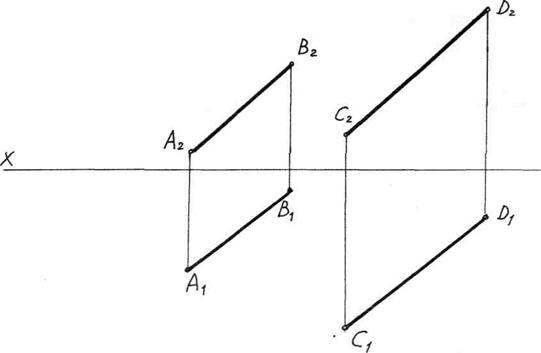
Задача 4.4 Побудувати сліди площини, заданої паралельними прямими АВ і CD
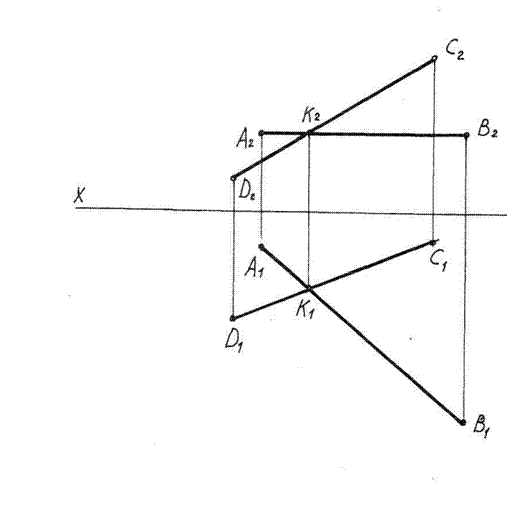 |
Задача 4.5 Побудувати сліди площини, заданої двома прямими, що перетинаються
5. ПОЗИЦІЙНІ ЗАДАЧІ
5.1. Взаємне положення прямої та площини.
5.1.1. Паралельність прямої та площини.
5.1.2. Перпендикулярність прямої та площини.
5.1.3. Перетин прямої з площиною.
5.2. Взаємне положення двох площин.
5.2.1. Паралельні площини.
5.2.2. Перетин площин.
5.2.3. Перпендикулярні площини.
5.3. Розв’язування задач по темі «Позиційні задачі».
5.1. Взаємне положення прямої та площини
5.1.1. Паралельність прямої та площини
Приклад 5.1.
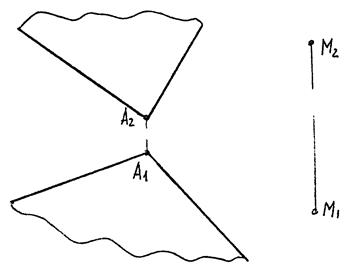
|
| Рис. 5.1 |
5.1.2. Перпендикулярність прямої та площини
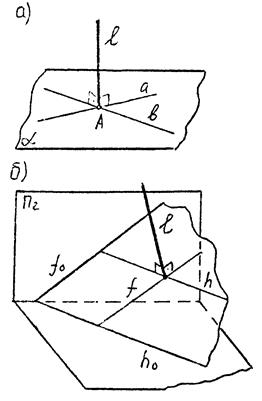
|
| Рис. 5.2 |
Приклад 5.2.
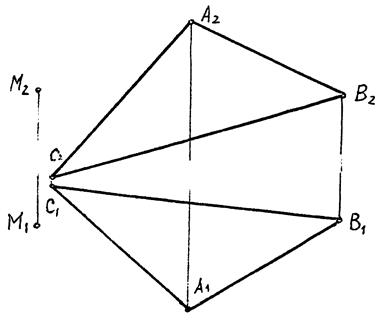
|
| Рис. 5.3 |
5.1.3. Перетин прямої з площиною
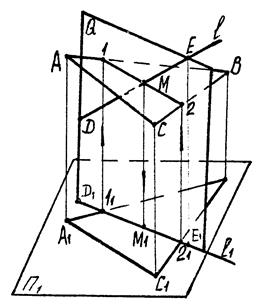
|
| Рис. 5.4 |
Приклад 5.3.
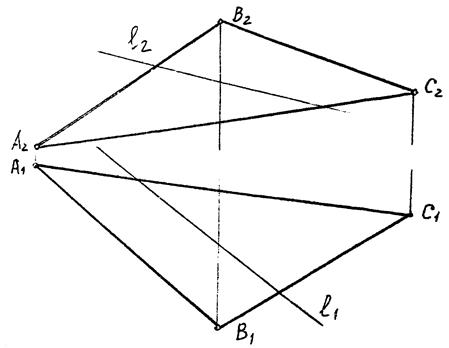
|
| Рис. 5.5 |
5.2. Взаємне положення двох площин
5.2.1. Паралельні площини
Приклад 5.4.
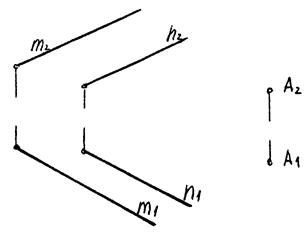
|
| Рис. 4.6 |
5.2.2. Перетин площин
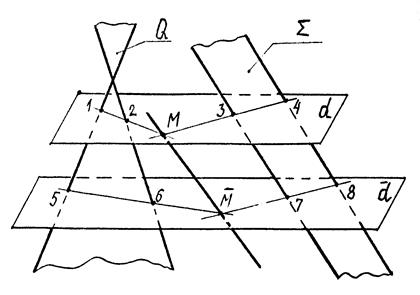
|
| Рис. 5.7 |
Приклад 5.5.
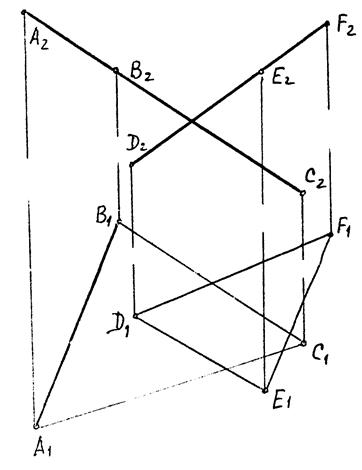
|
| Рис. 5.8 |
Приклад 5.6.
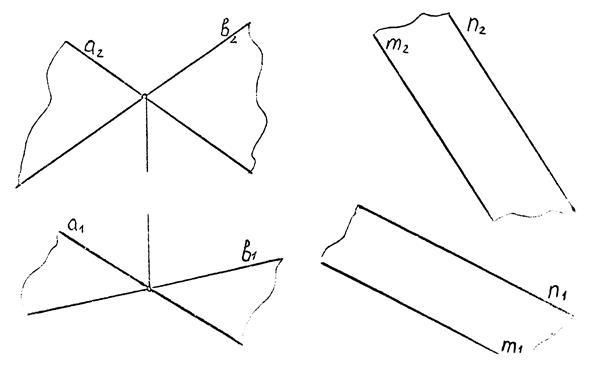
|
| Рис. 5.9 |
5.2.3. Перпендикулярні площини
Приклад 5.7.
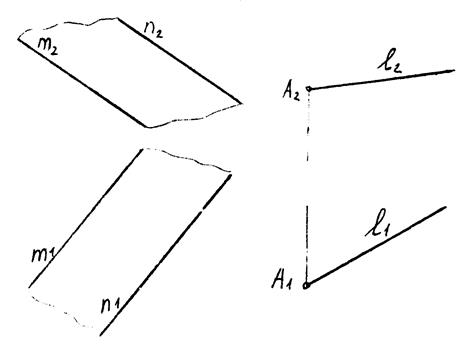
|
| Рис. 5.10 |
5.3. Розв’язування задач по темі «Позиційні задачі»
Задача 5.1. Побудувати горизонтальну проекцію прямої АВ, коли відомо, що вона паралельна площині Q (СD∩CK).
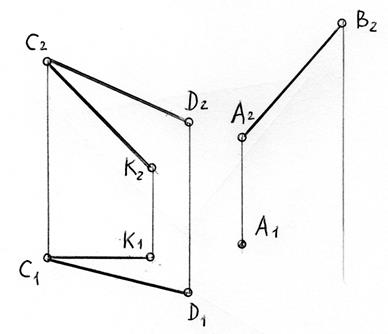
Задача 5.2. Побудувати точку перетину прямої DE з площиною ΔАВС, а також визначити видимість.
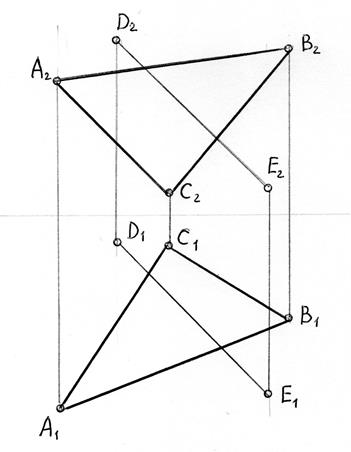
Задача 5.3. В точці D провести площину, яка паралельна до площини Σ (АВ∩ВС).
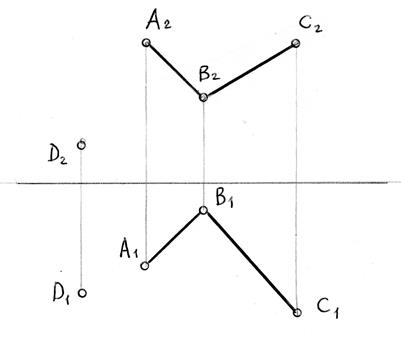
Задача 5.4. Побудувати площину Q, котра проходить через пряму (DE) і перпендикулярна заданій площині ΔАВС. Побудувати лінію перетину площини Q і ΔABC.
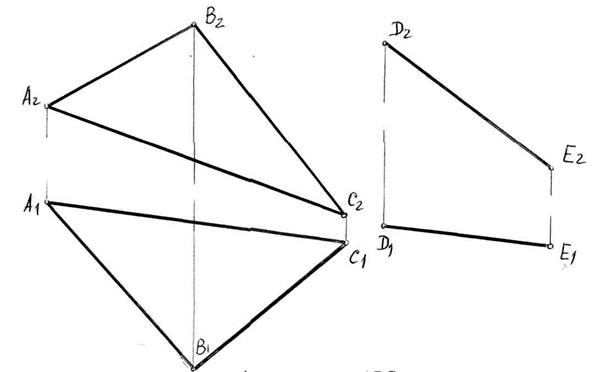
Задача 5.5. Визначити відстань від точки А до заданої площини (m || n).
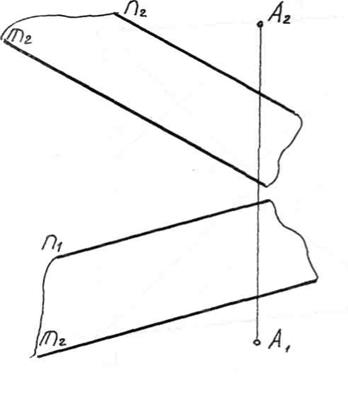
Задача 5.6 . Визначити відстань від точки А до прямої (ВС)
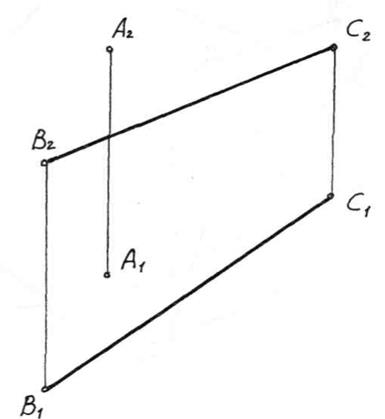
Задача 5.7. Побудувати лінію перетину двох площин і визначити їх взаємну видимість по конкуруючим точкам.
6. ПЕРЕТВОРЕННЯ ПРОЕКЦІЙ
6.1. Суть перетворення та його методи.
6.2. Спосіб заміни площин проекцій.
6.3. Розв’язування чотирьох основних задач способом заміни площин проекцій.
6.4 Спосіб обертання навколо проектуючих прямих.
6.5 Спосіб плоскопаралельного переміщення.
6.6 Спосіб обертання навколо лінії рівня.
6.7. Розв’язування метричних задач.
6.1. Суть перетворення та його методи
6.2. Спосіб заміни площин проекцій
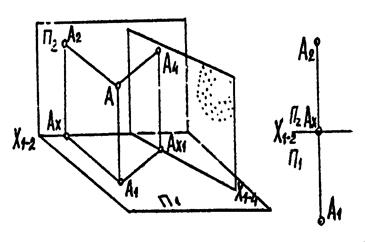
|
| Рис. 5.1 |
6.3. Розв’язування чотирьох основних задач способом заміни площин проекцій
А) 1-а основна задача
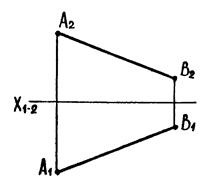
|
| Рис. 6.2 |
Б) 2-а основна задача
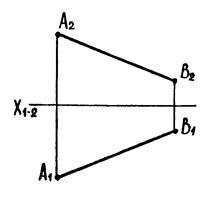
|
| Рис. 6.3 |
В) 3-я основна задача
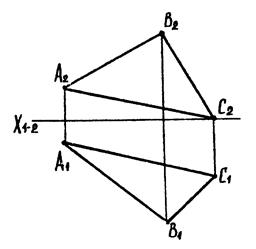
|
| Рис. 6.4 |
Г) 4-а основна задача
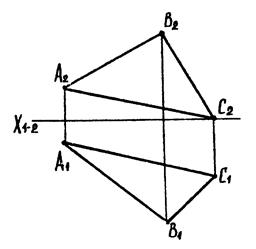
|
| Рис. 6.5 |
6.4 Спосіб обертання навколо проектуючих прямих.
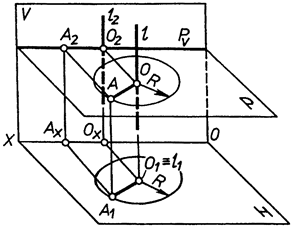
|
| Рис. 6.6 |
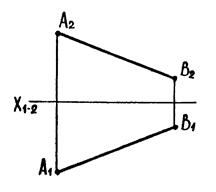
|
| Рис. 6.7 |
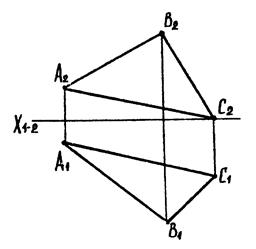
|
| Рис. 6.8 |
6.5 Спосіб плоскопаралельного переміщення.
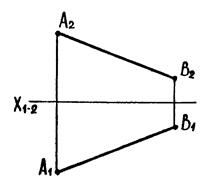
|
| Рис. 6.9 |
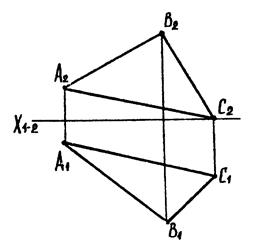
|
| Рис. 6.10 |
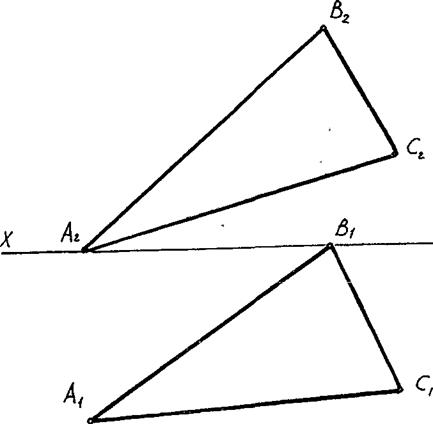
6.6 Спосіб обертання навколо лінії рівня.
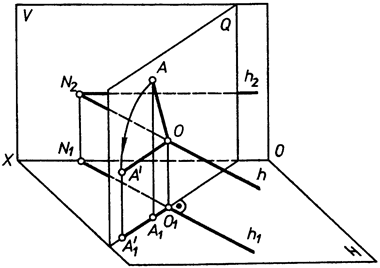
|
| Рис. 6.11 |
|
| Рис. 6.12 |
6.7. Розв’язування метричних задач.
Задача 6.1. Визначити натуральну величину відрізка АВ та кути нахилу його до площин проекцій П1 і П2 способом заміни площин проекцій.
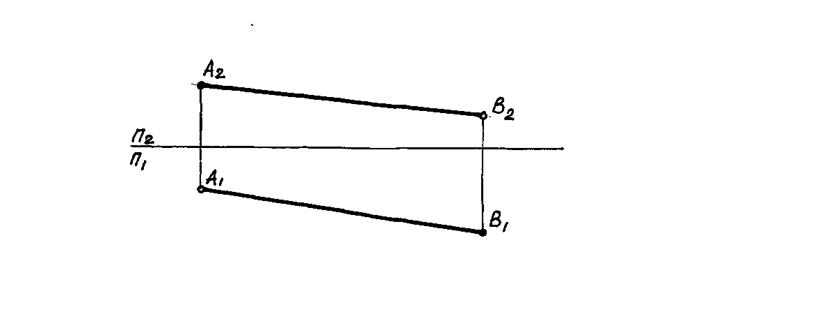
Задача 6.2. Визначити відстань між двома паралельними площинами, з яких одна задана трикутником АВС, а інша - трикутником DFE способом заміни площин проекцій.
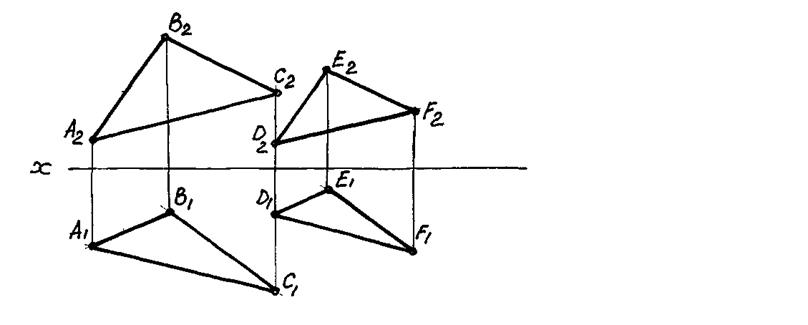
Задача 6.3. Способом заміни площин проекцій визначити відстань між ребром SB і стороною основи АС піраміди SАВС. Побудувати проекції спільного перпендикуляра до SB та AC.
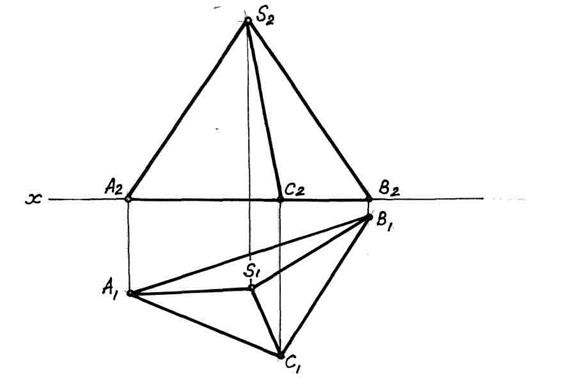
Задача 6.4. Визначити відстань від точки А до площини α (hα, fα ) способом заміни площин проекцій.
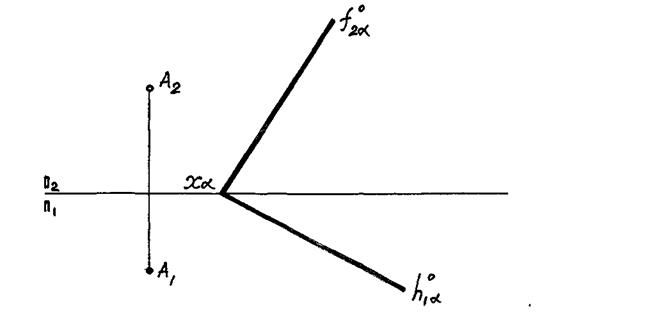
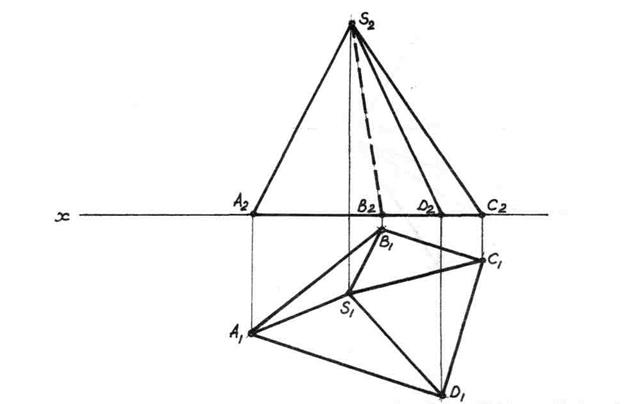
Задача 6.5. Визначити натуральну величину ребер AS,CS,BS та DS піраміди ABCDS, використовуючи спосіб обертання навколо осі, перпендикулярної до площини П1
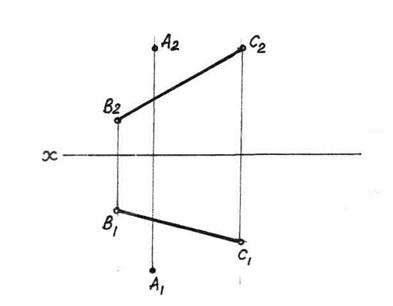
Задача 6.6. Визначити відстань від точки А до прямої ВС.
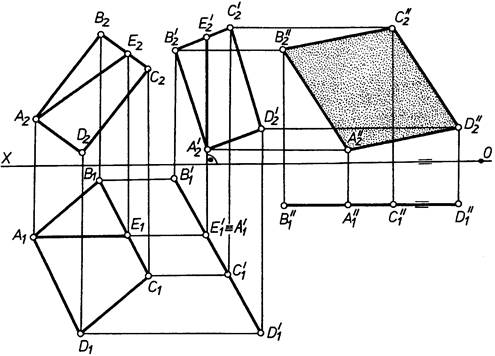
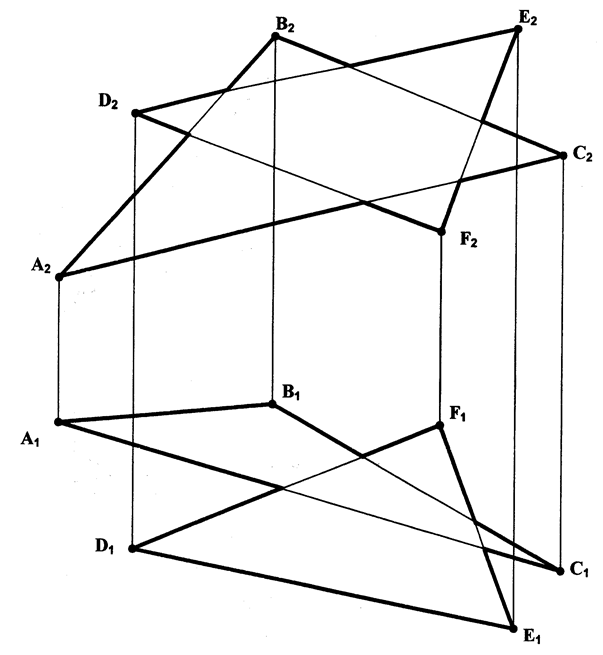
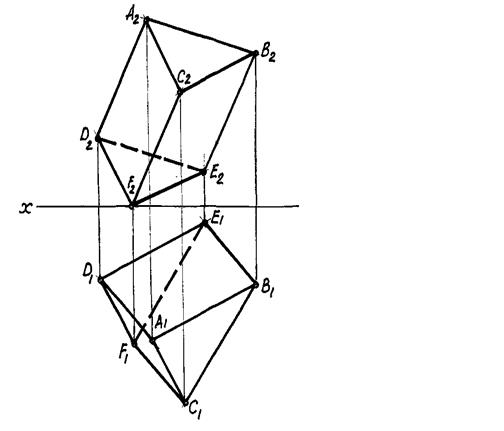
Задача 6.7. Визначити відстань між ребрами АD, CF і BE похилої призми АВCDEF способом плоскопаралельного переміщення
.
7. КРИВІ ЛІНІЇ
7.1. Основні поняття та визначення кривих ліній.
7.2 Способи завдання кривих ліній.
7.3 Плоскі криві.
7.3.1. Властивості плоских кривих.
7.3.2. Класифікація точок плоских кривих.
7.4. Просторові криві лінії.
7.5 Розв'язування задач з теми «Криві лінії».
7.1. Основні поняття та визначення кривих ліній.
7.2 Способи завдання кривих ліній.
7.3 Плоскі криві.
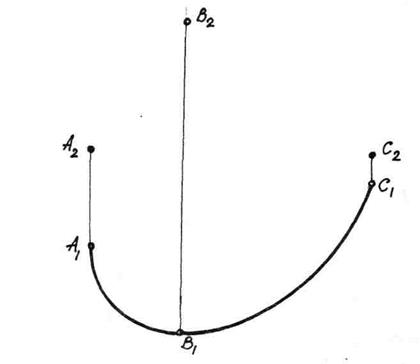
|
| Рис. 7.1 |
7.3.1. Властивості плоских кривих.
7.3.2. Класифікація точок плоских кривих.
7.4. Просторові криві лінії.
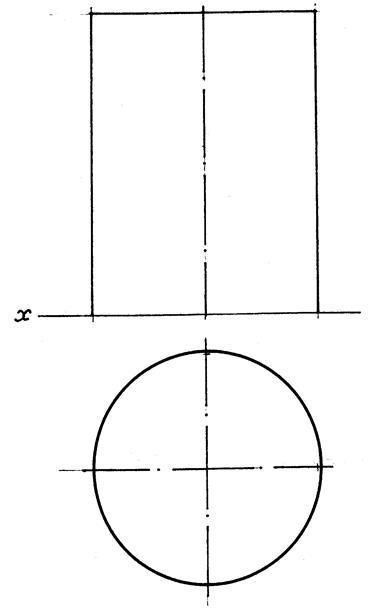
|
| Рис. 7.2 |
7.5 Розв'язування задач з теми «Криві лінії».
Задача 7.1. Побудувати проекції конічної гвинтової лінії.
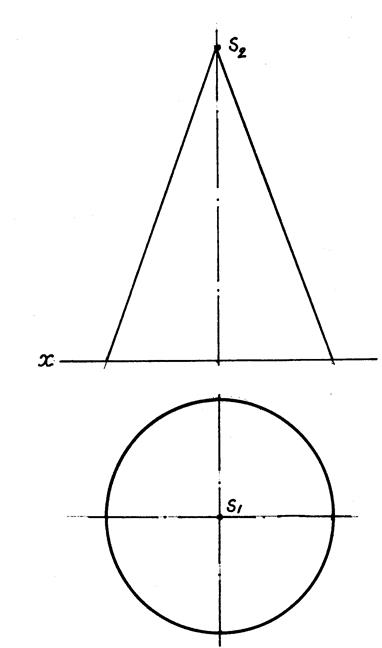
8. ГРАННІ ПОВЕРХНІ ТА МНОГОГРАННИКИ
8.1. Гранні поверхні. Основні поняття та визначення.
8.2. Многогранники.
8.2.1. Комплексний кресленик піраміди.
8.2.2. Комплексний кресленик призми.
8.3. Перетин многогранника з площиною.
8.4. Перетин многогранника з прямою.
8.4.1. Алгоритм побудови точок перетину многогранника прямою лінією.
8.4.2. Приклад побудови точок перетину многогранника з прямою лінією.
8.5. Взаємний перетин многогранників.
8.5.1. Алгоритм побудови лінії перетину многогранників.
8.5.2. Приклад побудови лінії перетину многогранників
8.6. Розв’язування задач по темі «Гранні поверхні та многогранники».
8.1. Гранні поверхні. Основні поняття та визначення
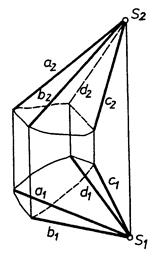
|
| Рис. 8.1 |
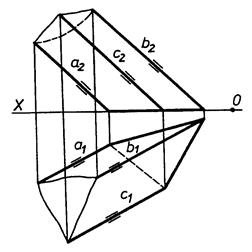
|
| Рис. 8.2 |
8.2. Многогранники
8.2.1. Комплексний кресленик піраміди
 |
8.2.2. Комплексний кресленик призми
 |
8.3. Перетин многогранника з площиною
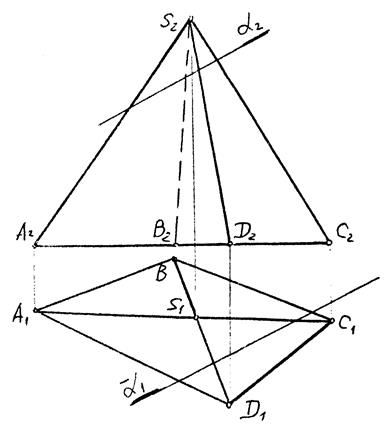
|
| Рис. 8.3 |
8.4. Перетин многогранника з прямою
8.4.1. Алгоритм побудови точок перетину многогранника прямою лінією
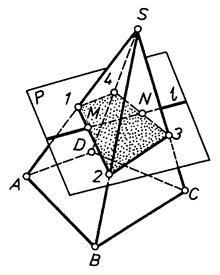
|
| Рис. 8.4 |
8.4.2. Приклад побудови точок перетину многогранника з прямою лінією
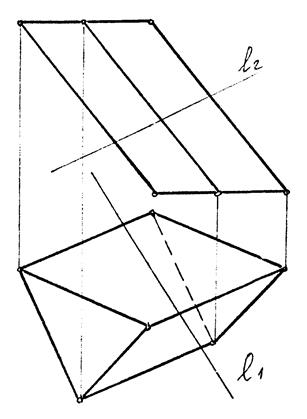
|
| Рис. 8.5 |
8.5. Взаємний перетин многогранників
8.5.1. Алгоритм побудови лінії перетину многогранників
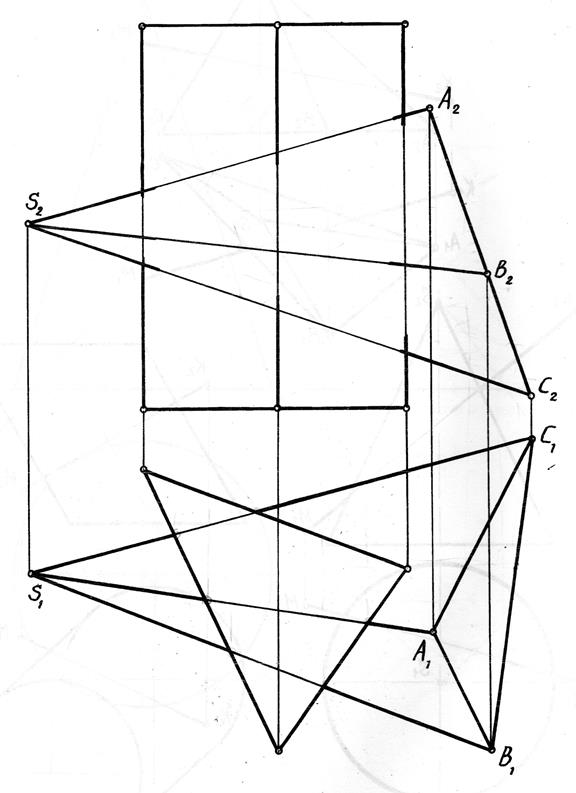
8.5.2. Приклад побудови лінії перетину многогранників
|
| Рис. 8.6 |
8.6. Розв’язування задач по темі «Гранні поверхні та многогранники»
Задача 8.1.. Добудувати профільну проекцію піраміди та проекції точок А, В, С, i D, які належать граням піраміди.

Задача 8.2. Побудувати три проекції нахиленої призми за заданою основою АВС і ребром А¢А. Визначити видимість ребер призми і побудувати недостатню проекцію точки 1, що належить поверхні призми.
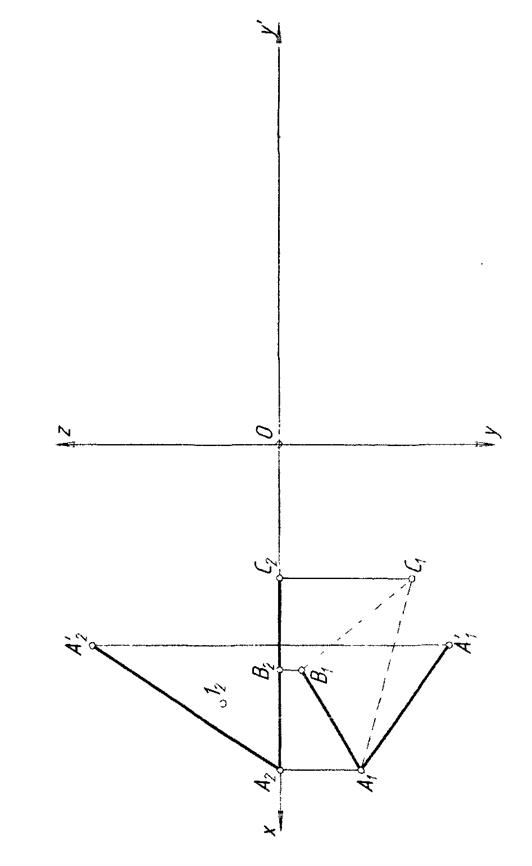
Задача 8.3. Побудувати три проекції перерізу піраміди проекційною площиною. Визначити розмір перерізу.
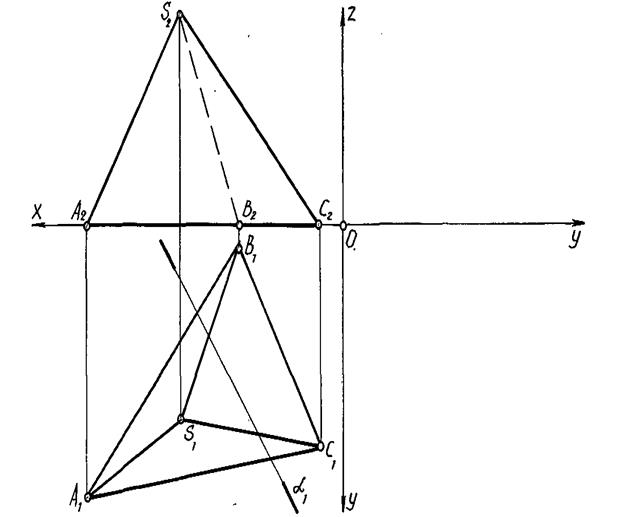
Задача 8.4. Побудувати точки перетину прямої з многогранником.
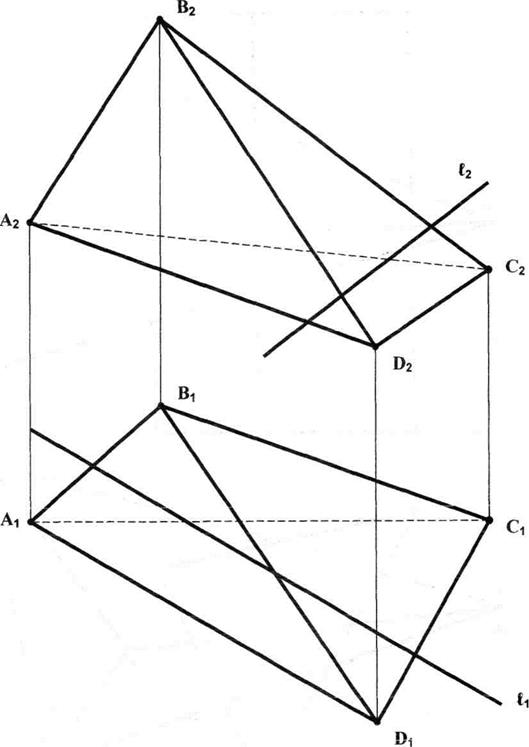
9. КРИВІ ПОВЕРХНІ
9.1. Криві поверхні. Загальні відомості.
9.1.1. Основні способи задання поверхні.
9.1.2. Визначник поверхні.
9.1.3. Прямокутні (ортогональні) проекції поверхні.
9.2. Класифікація кривих поверхонь.
9.3. Лінійчаті поверхні.
9.3.1. Розгортні лінійчаті поверхні.
9.3.2. Нерозгортні лінійчаті поверхні.
9.3.2.1. Лінійчаті поверхні з трьома напрямними
9.3.2.2. Лінійчаті поверхні з площиною паралелізму
9.4. Поверхні обертання.
9.4.1. Поверхні обертання довільного вигляду.
9.4.2. Поверхні обертання особливого вигляду.
9.4.2.1. Твірна поверхні обертання – пряма.
9.4.2.2. Твірна поверхні обертання – коло.
9.5. Розв’язування задач по темі «Криві поверхні».
9.1. Криві поверхні. Загальні відомості
9.1.1. Основні способи задання поверхні
А)
Б)
В)
9.1.2. Визначник поверхні
9.1.3. Прямокутні (ортогональні) проекції поверхонь
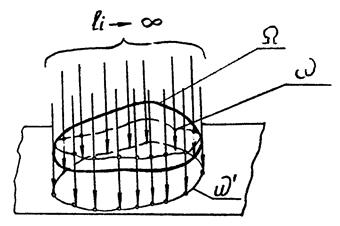
|
| Рис. 9.1 |
9.2. Класифікація кривих поверхонь
9.3. Лінійчаті поверхні
9.3.1. Розгортні лінійчаті поверхні
А) конічна -
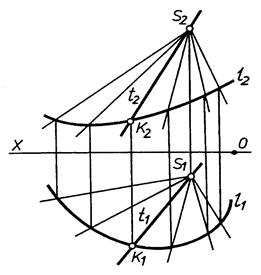
|
| Рис. 9.2 |
Б) циліндрична -
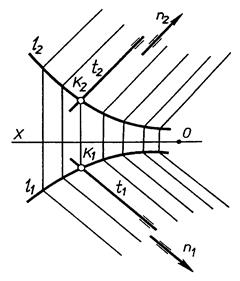
|
| Рис. 9.3 |
В) поверхня з ребром звороту -
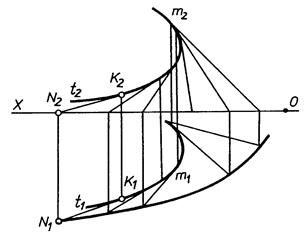
|
| Рис. 9.4 |
9.3.2. Нерозгортні лінійчаті поверхні
9.3.2.1. Лінійчаті поверхні з трьома напрямними
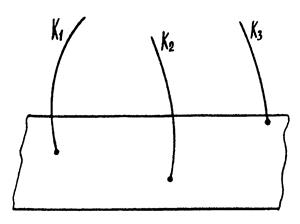
|
| Рис. 9.5 |
9.3.2.2. Лінійчаті поверхні з площиною паралелізму
А) коса площина –
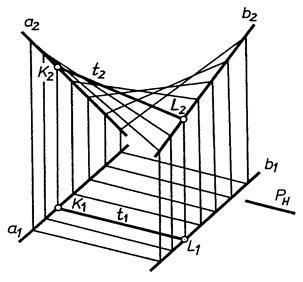
|
| Рис. 9.6 |
Б) коноїд –
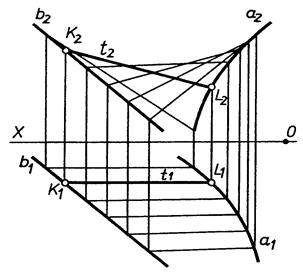
|
| Рис. 9.7 |
В) циліндроїд –
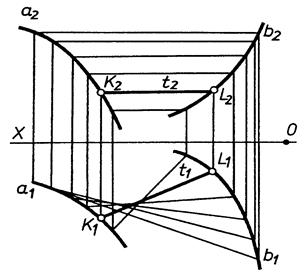
|
| Рис. 9.8 |
9.4. Поверхні обертання
9.4.1. Поверхні обертання довільного вигляду
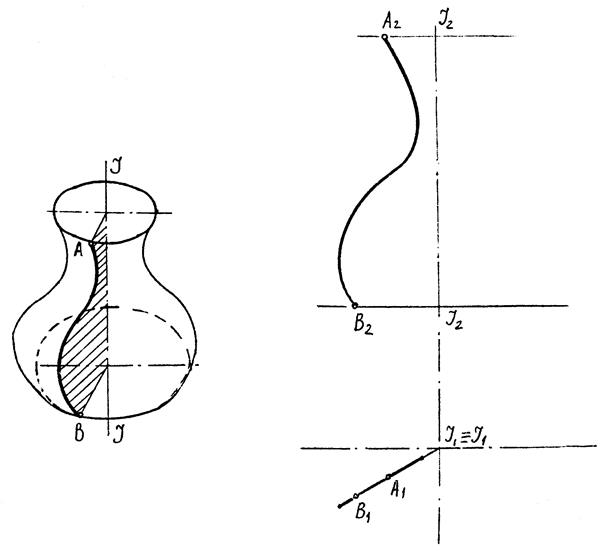
|
| Рис. 9.9 |
9.4.2. Поверхні обертання особливого вигляду
9.4.2.1. Твірна поверхні обертання – пряма
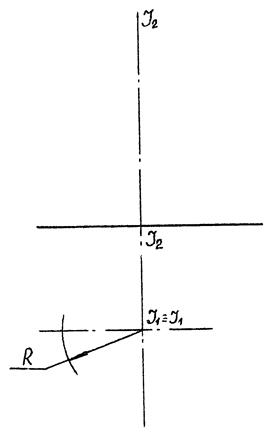
|
| Рис. 9.10 |
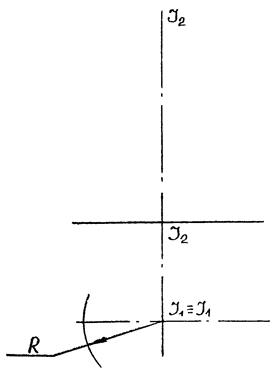
|
| Рис. 9.11 |
9.4.2.2. Твірна поверхні обертання – коло
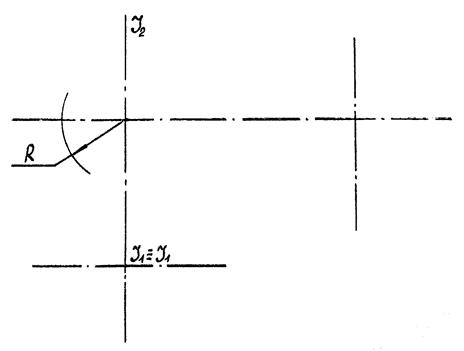
|
| Рис. 9.12 |
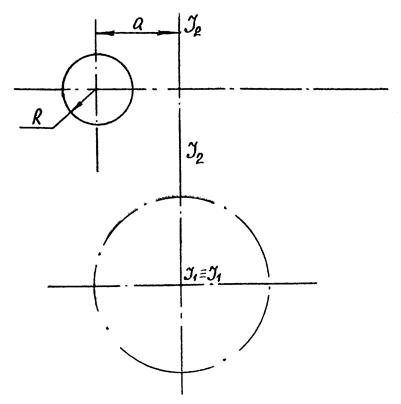
|
| Рис. 9.13 |
9.5. Розв’язування задач по темі «Криві поверхні»
Задача 9.1. Знайти лінію перетинуциліндричної поверхні, яка задана напрямною АВ і твірної CD, з площиною П1.
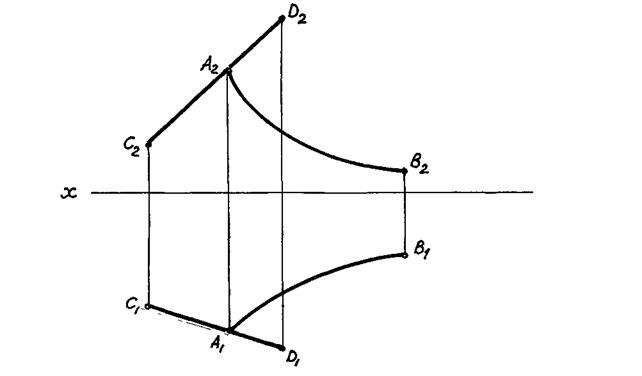
Задача 9.2. Знайти лінію перетину конічної поверхні, яка задана вершиною S і напрямною АB, з площиною П1.
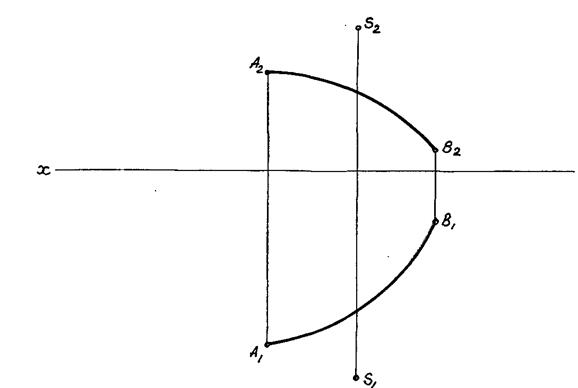
Задача 9.3. Побудувати невистачаючі проекції кривої АВ, що належить:
а) циліндру обертання
| б) конусу обертання
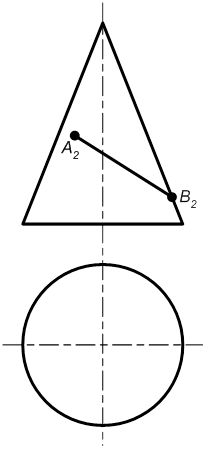
|
в) сфері
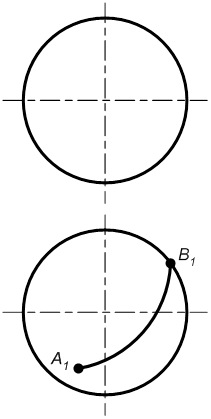
| г) тору
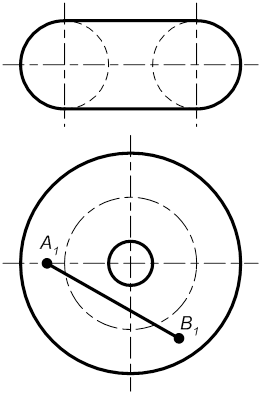
|
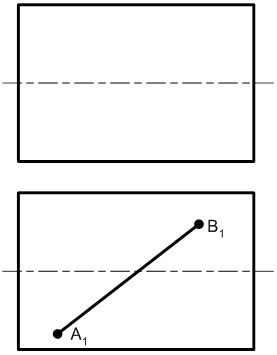
Задача 9.4. Побудувати відсутні проекції точок, що належать поверхням:
а) похилого циліндру, б) похилого конуса, в) сфері, г) поверхні обертання.
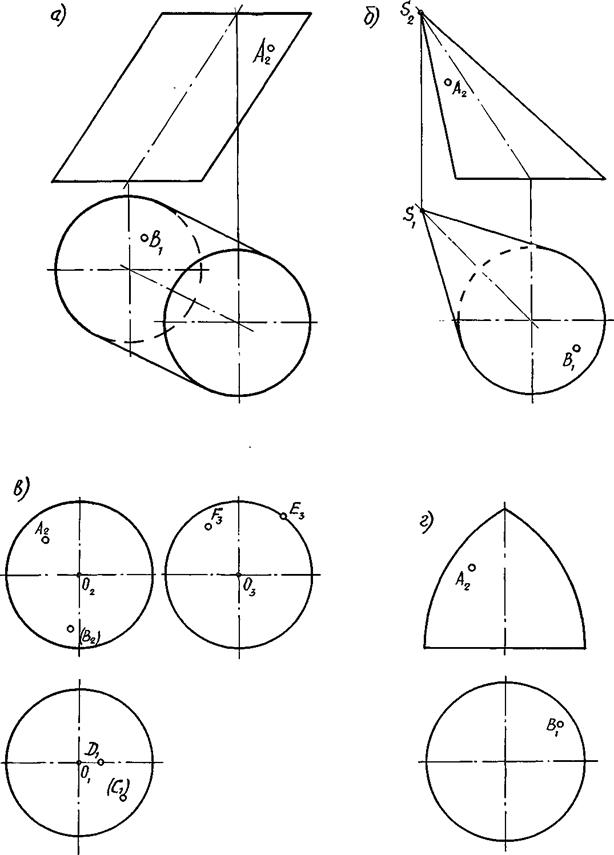
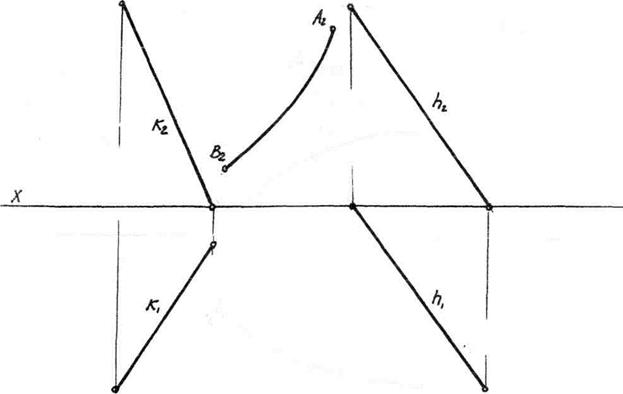
Задача 9.5. Побудувати контур проекцій відсіку поверхні і другу проекцію кривої (АВ), що належить:
а) циліндроїду з площиною паралелізму p1;
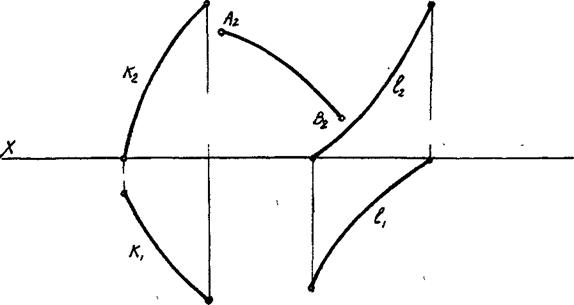
б) гіперболічному параболоїду з площиною паралелізму p1
10. ПОЗИЦІЙНІ ЗАДАЧІ З КРИВИМИ ПОВЕРХНЯМИ
10.1. Перетин поверхонь площиною.
10.1.1. Алгоритм побудови лінії перетину кривої поверхні площиною.
10.1.2. Конічні перерізи.
10.2. Перетин кривих поверхонь прямими лініями.
10.2.1. Алгоритм побудови точок перетину кривої поверхні прямою лінією.
10.2.2. Приклади побудови точок перетину кривої поверхні прямою лінією.
10.3. Взаємний перетин поверхонь.
10.3.1. Загальні відомості.
10.3.2. Побудова лінії перетину поверхонь способом допоміжних січних площин.
10.3.3. Побудова лінії перетину поверхонь способом допоміжних кульових поверхонь.
10.3.4. Побудова лінії перетину поверхонь другого порядку (окремі випадки).
10.4. Розв’язування задач по темі «Позиційні задачі з кривими поверхнями».
10.1. Перетин поверхонь площиною
10.1.1. Алгоритм побудови лінії перетину кривої поверхні площиною
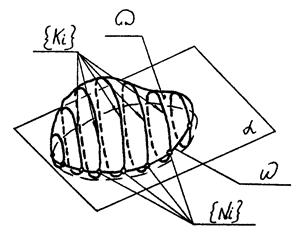
|
| Рис. 10.1 |
Приклад 10.1.
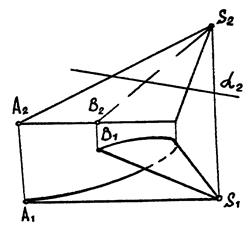
|
| Рис. 10.2 |
Приклад 10.2.
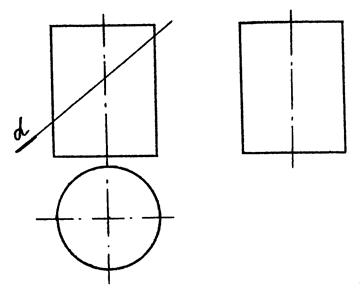
|
| Рис. 10.3 |
10.1.2. Конічні перерізи
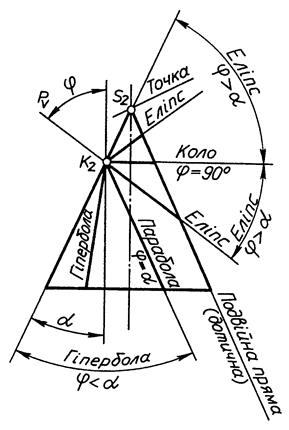
|
| Рис.10 8.4 |
Приклад 10.3.
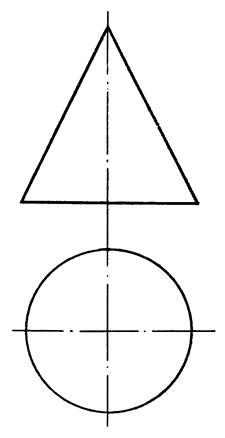
|
| Рис. 10.5 |
| Приклад 10.4. |
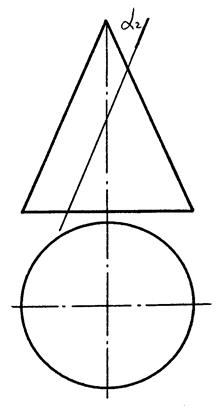
|
| Рис. 10.6 |
10.2. Перетин кривих поверхонь з прямими лініями
10.2.1. Алгоритм побудови точок перетину кривої поверхні з прямою лінією
10.2.2. Приклади побудови точок перетину кривої поверхні з прямою лінією
Приклад 10.5.
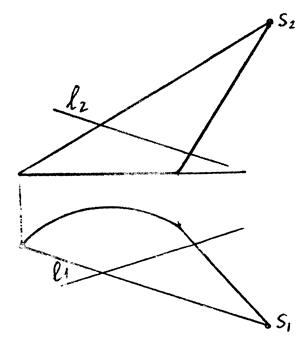
|
| Рис. 10.7 |
Приклад 10.6.
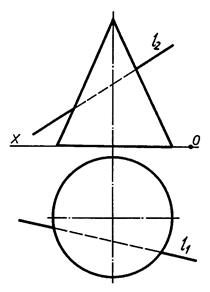
|
| Рис. 10.8 |
10.3. Взаємний перетин поверхонь
10.3.1. Загальні відомості
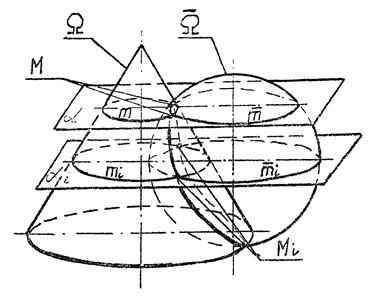
|
| Рис. 10.9 |
10.3.2. Побудова лінії перетину поверхонь способом допоміжних січних площин
Приклад 10.7.
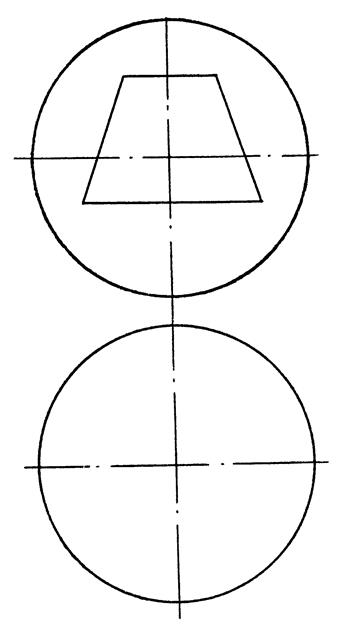
|
| Рис. 10.10 |
Приклад 10.8.
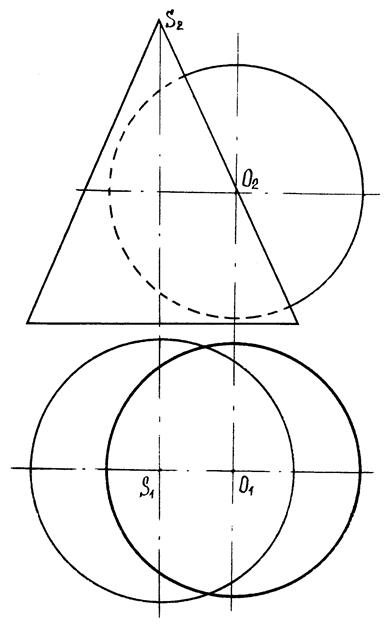
|
| Рис. 10.11 |
10.3.3. Побудова лінії перетину поверхонь способом допоміжних кульових поверхонь
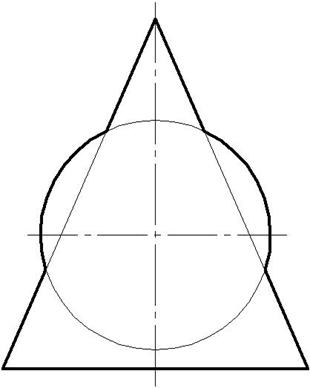
|
Рис. 10.12
Приклад 10.9.
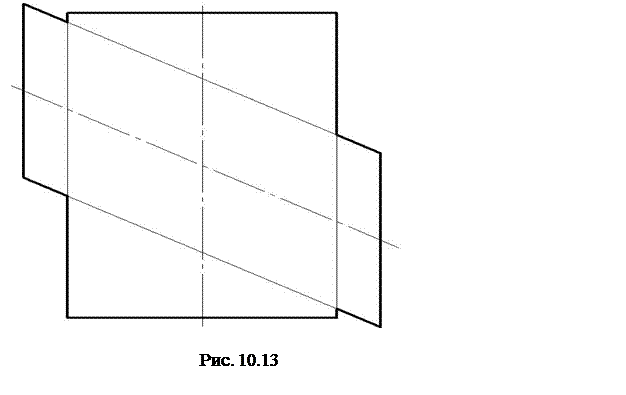
|
10.3.4. Побудова лінії перетину поверхонь другого порядку (окремі випадки)
А)
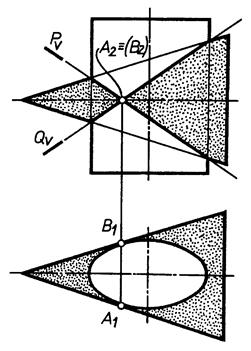
| |||
| Рис. 10.14 | |||
| Б) | |||
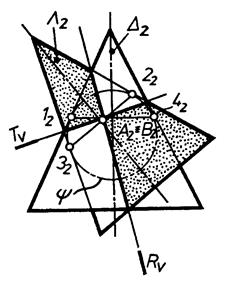
| |||
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|