Хелпикс

Главная

Контакты

Случайная статья



Упругие характеристики однонаправленного слоя

Стр 1 из 2Следующая ⇒


37.Упругие характеристики однонаправленного слоя

Вычисление продольного коэффициента Пуассона.

Рассмотрим вычис.коэффициента Пуассона однонаправленного слоя

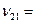
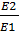
-относительные поперечная и продольная деформация соответственно при действии напряжения G1.В отличие от изотропных материалов в композитах коэффициент Пуассона имеет два индекса : первый показывает направление действия напряжения ,второй-направление поперечной деформации .Деформация в поперечном направлении состоит из деформации части, занятой волокнами ,и части, занятой матрицей.

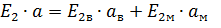, где 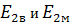 - относительные поперечные деформации частей, занимаемых волокнами и матрицей; a,  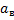и 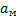 –поперечные размеры сечения однонаправленного слоя и частей, занятых волокнами и матрицей соответственно.

Разделим левую и правую части на a. Получим

) ,где 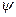=  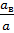. Выразим относительные поперечные деформации однонаправленного слоя и частей, занимаемых волокном и матрицей, через их продольные деформации и коэффициенты Пуассона.

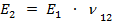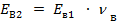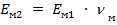 ;  ; (2)

Где 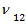-продольно-поперечный коэффициент Пуассона однонаправленного слоя ;

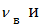
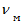  -коэффициенты Пуассона волокна и матрицы соответственно.

Подставляя (1) в (2) и учитывая, что продольные деформации однонаправленного слоя, волокон, матрицы одинаковы, т.е 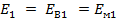 , получим

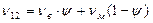(3)


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.