Лабораторная работа №3.. Численное интегрирование

Лабораторная работа №3.

Численное интегрирование

Цель работы: найти приближенное значение определенного интеграла с требуемой точностью различными численными методами.

Исходные данные:

1. Пользователь выбирает функцию, интеграл которой требуется вычислить (3-5 функций), из тех, которые предлагает программа.

2. Пределы интегрирования задаются пользователем.

3. Точность вычисления задаются пользователем.

4. Начальное значение числа разбиения интервала интегрирования: n=4.

5. Ввод исходных данных осуществляется с клавиатуры.

Программная реализация задачи:

1. Реализовать в программе методы по выбору пользователя:

· Метод прямоугольников (3 модификации: левые, правые, средние)

· Метод трапеций

· Метод Симпсона

2. Методы должны быть оформлены в виде отдельной(ого) функции/класса.

3. Вычисление значений функции оформить в виде отдельной(ого) функции/класса.

4. Предусмотреть вывод результатов: значение интеграла, число разбиения интервала интегрирования для достижения требуемой точности.

Вычислительная реализация задачи:

1. Вычислить интеграл, приведенный в таблице (столбец 3), точно.

2. Вычислить интеграл методом, указанным в таблице (столбец 4) при n=10.

3. Определить абсолютную погрешность вычислений.

4. В отчете отразить последовательные вычисления.

Оформить отчет, который должен содержать:

1. Титульный лист.

2. Цель лабораторной работы.

3. Порядок выполнения работы.

4. Блок-схемы используемых методов, их рабочие формулы.

5. Листинг программы.

6. Результаты выполнения программы.

7. Вычисление заданного интеграла.

8. Выводы

Вариант	Реализация метода в программе	Интеграл	Метод
	прямоугольников		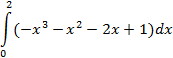Симпсона
	трапеций		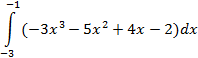прямоугольников
	Симпсона		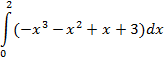трапеций
	прямоугольников		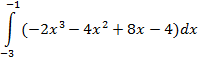Симпсона
	трапеций		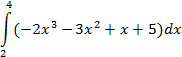Симпсона
	Симпсона		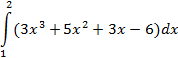прямоугольников
	прямоугольников		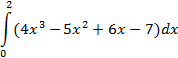трапеций
	трапеций		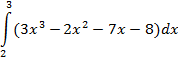Симпсона
	Симпсона		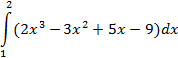трапеций
	прямоугольников		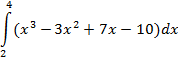Симпсона
	трапеций		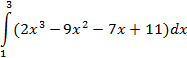Симпсона
	Симпсона		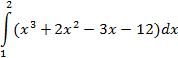прямоугольников
	прямоугольников		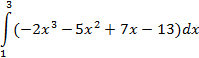Симпсона
	трапеций		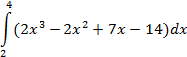прямоугольников
	Симпсона		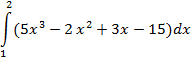трапеций
	прямоугольников		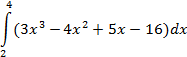Симпсона
	трапеций		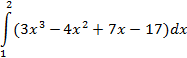Симпсона
	Симпсона		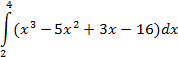прямоугольников
	прямоугольников		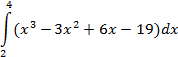трапеций
	трапеций		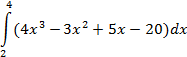Симпсона
	Симпсона		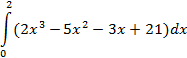трапеций
	прямоугольников		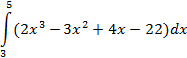Симпсона
	трапеций		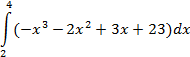Симпсона
	Симпсона		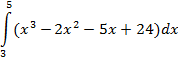прямоугольников
	прямоугольников		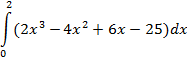Симпсона