Контакты

Случайная статья

Задания к экзаменам

⇐ ПредыдущаяСтр 2 из 2

Задания к экзаменам

1. Даны вершины треугольника ABC: A (-2, 4), В (3, 1), С (10, 7).

Найти: а) уравнение стороны АВ; б) уравнение высоты CH;

2. Даны вершины треугольника ABC: A (-2, 4), В (3, 1), С (10, 7).

Найти: а) уравнение медианы АМ; б) уравнение прямой, проходящей через вершину С параллельно стороне АВ.

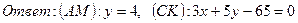
3. Записать уравнение прямой, проходящей через точку A(3, 1) перпендикулярно к прямой BC, если В(2, 5), С(1, 0).

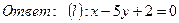
4. Доказать, что четырехугольник ABCD - трапеция, если A(3, 6), В(5, 2), С(-1, -3),

D(-5,5).

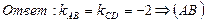½½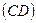

5. Треугольник задан вершинами А(2; -1), В(-7, 3) и С(-1, -5). Составить уравнение биссектрисы угла С.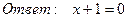

6.

7. Найти производную функции

,

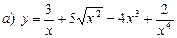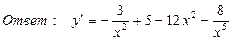
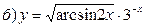
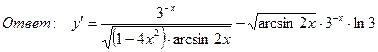
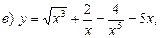
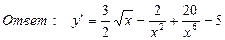
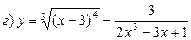
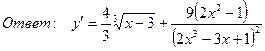
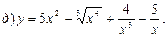
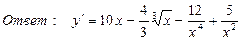
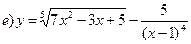
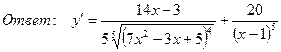
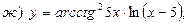
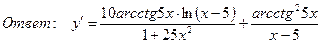
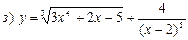
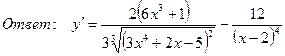
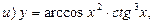
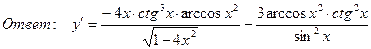
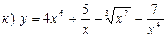
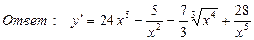
8. Найти производную функции, если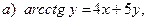

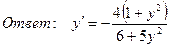
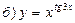
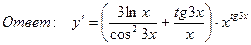
9. Найти производную функции :

,

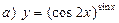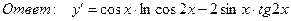
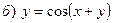
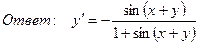
10. Провести полное исследование функции и построить график

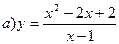
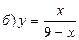
11. Найти наименьшее и наибольшее значения функции 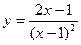на отрезке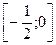

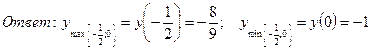
12. Записать уравнение касательной и нормали к графику функции

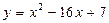в точке с абсциссой .

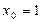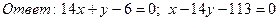
13. Вычислить площадь фигуры, ограниченной линиями: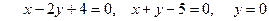

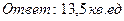
14. Даны две матрицы A и B. Найти: а) AB; б) BA:А = 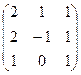, В = .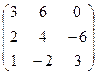

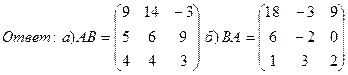
15. Даны две матрицы A и B. Найти: а) AB; б) BAА = 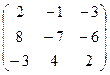, В =.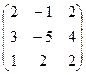

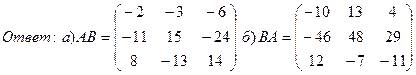
16. Для матриц А и В найт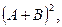и если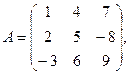

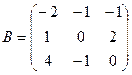
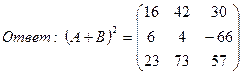
17. Найти матрицу, обратную данной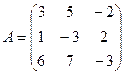

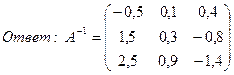
18. Даны две матрицы A и B: , .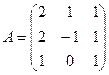

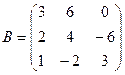Найти: а) AB; б)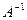

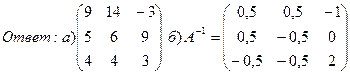
19. Вычислить определители:

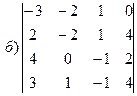
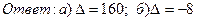
20. Решить систему уравнений по формулам Крамера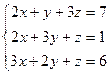

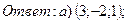
21. Решить систему уравнений по формулам методом Гаусса

а) 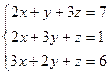б)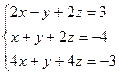

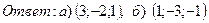
22. Решить систему с помощью обратной матрицы (матричным методом):

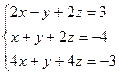
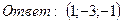
23. Найти интегралы:

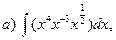
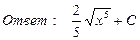
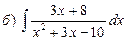
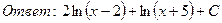
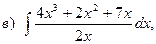
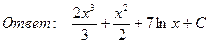
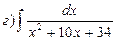
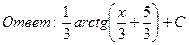
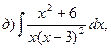
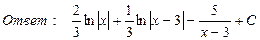
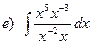
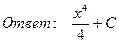
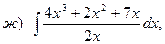
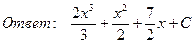
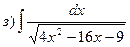
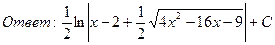
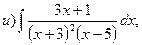
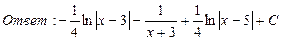
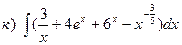
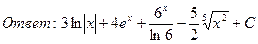
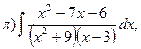
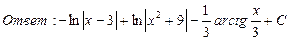
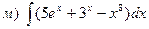
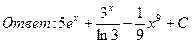
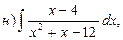
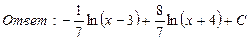
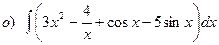
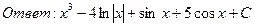
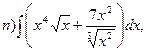
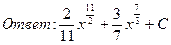
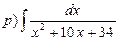
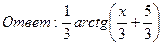
24. Найти площадь параллелограмма, построенного на векторах

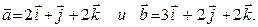
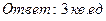
25. Найти объем параллелепипеда, построенного на векторах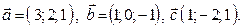

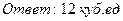
26. Найти пределы:

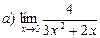
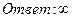
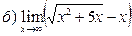
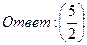
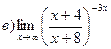
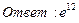
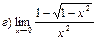
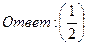
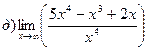
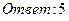
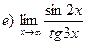
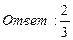
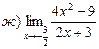
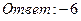
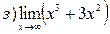
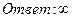
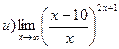
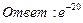
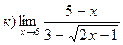
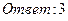
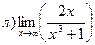
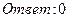
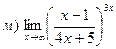
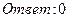
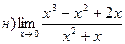
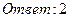
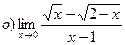
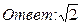
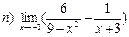
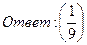
27. Решить дифференциальные уравнения:

а) ;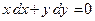

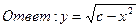
б) ;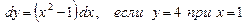

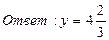
в) ;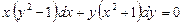

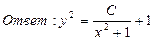
г) ;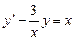

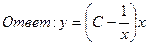
д) ;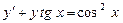

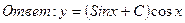
е) ;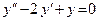

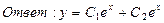
ж) ;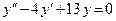

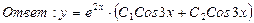
з) ;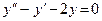

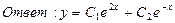
⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.