Контакты

Случайная статья

Сложение векторов и умножение вектора на число. Коллинеарность и компланарность векторов. Координаты вектора в аффинной системе координат.

Стр 1 из 2Следующая ⇒

1. Сложение векторов и умножение вектора на число. Коллинеарность и компланарность векторов. Координаты вектора в аффинной системе координат.

+

+

+

Сложение векторов.

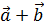
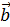
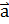
1)

2) 3)

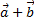
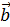
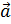
Умножение вектора на число.

1)

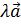
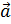
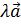
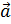
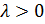2)

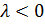
Векторы 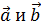являются коллинеарными тогда и только тогда, когда один из векторов можно выразить через другой умножением на число.

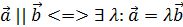
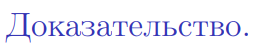
►Необходимость.

Пусть . Отложив 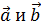от одной точки, получим, что оба вектора лежат на одной прямой. Если один из векторов, например, 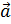равен 0, то .

; .

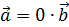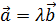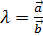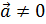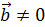1) Если и , то 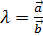, тогда ( )

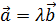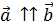2) 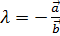, тогда ( )

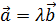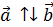Достаточность.

Пусть 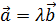, тогда ◄

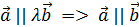Координаты вектора в аффинной системе координат.

Аффинная система координат на плоскости.

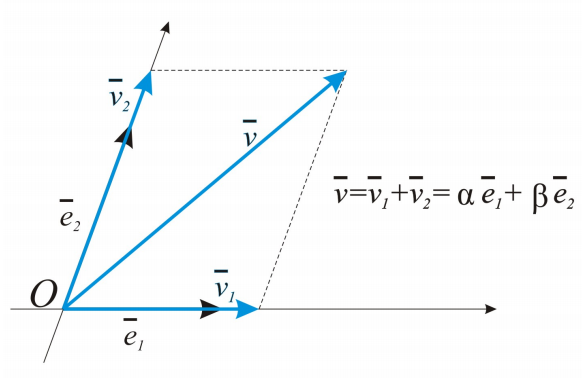
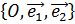
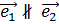
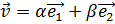
Тогда ( 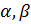) – координаты вектора 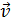в системе координат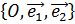

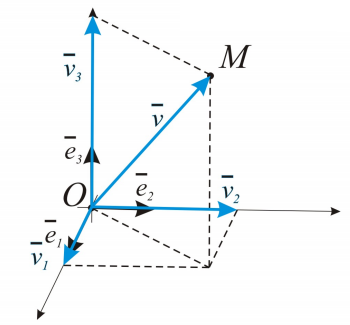Аффинная система координат в пространстве.

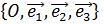не лежат в одной плоскости, будучи отложенными от одной точки.

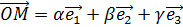
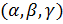– координаты точки М.

2. Скалярное и векторное произведения. Свойства, геометрический смысл этих произведений и их выражение в координатах.

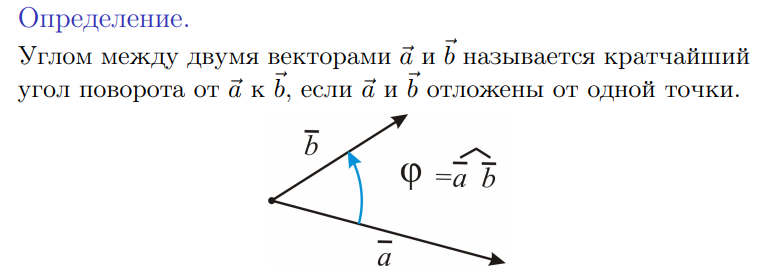
Геометрический смысл скалярного произведения.

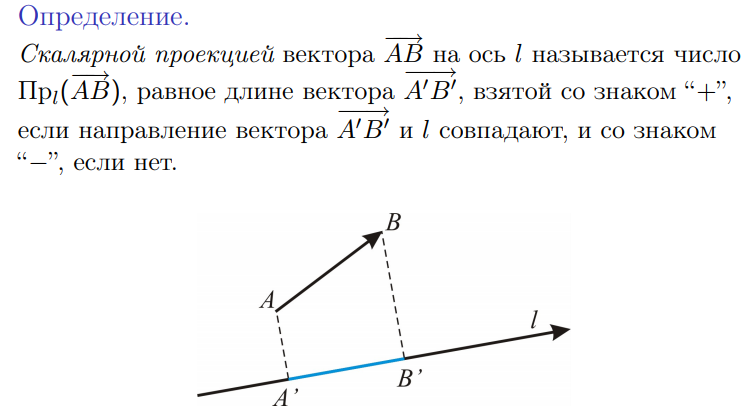
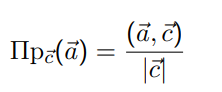
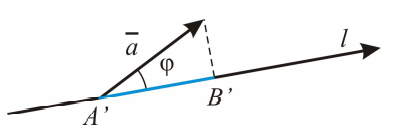Доказательство:

1)

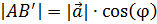
С другой стороны

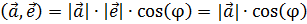
Таким образом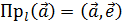

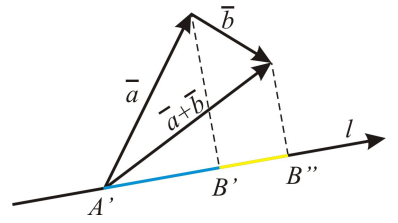
l

C

B

А

2)

1.

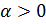
Из подобия △АВВ’ и △АСС’ следует, что

АС’ = 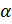AB’

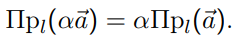
3)

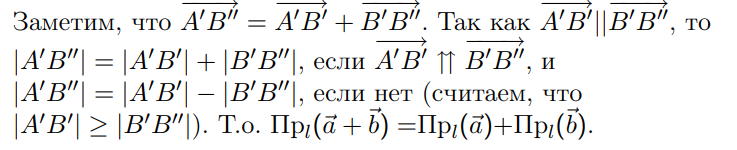
Свойства скалярного произведения.

1. Симметричность

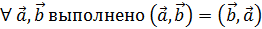
2. Линейность

·

·

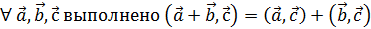
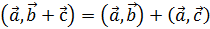
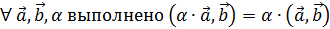
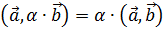
3. Положительная определенность

·

·

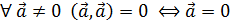
4.

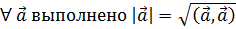
5. Критерий ортогональности

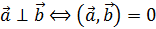
Доказательство

►

1)

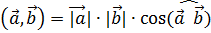
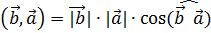
Т.к.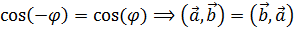

2) 1.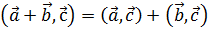

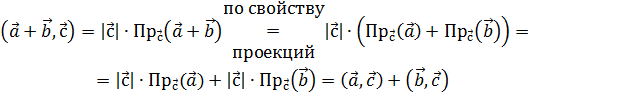
2.

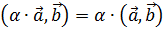
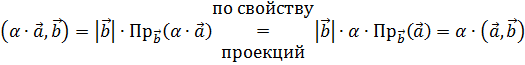
3) 1.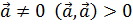

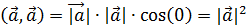
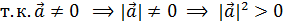
2.

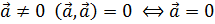
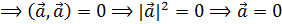
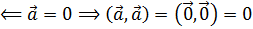
4)

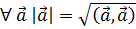
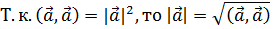
1)

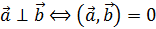
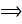
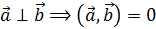
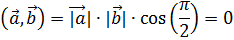
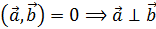
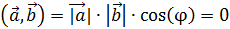
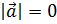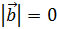или или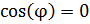

◄

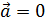
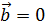
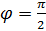
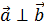
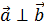
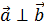Доказательство:

►

Вычислим длину АВ

1. По теореме Пифагора:

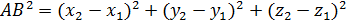
2. По теореме косинусов:

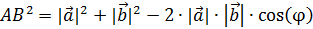
В

А

◄

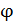
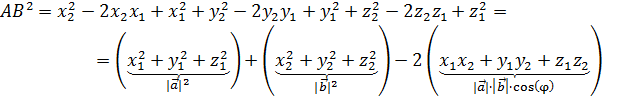
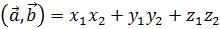
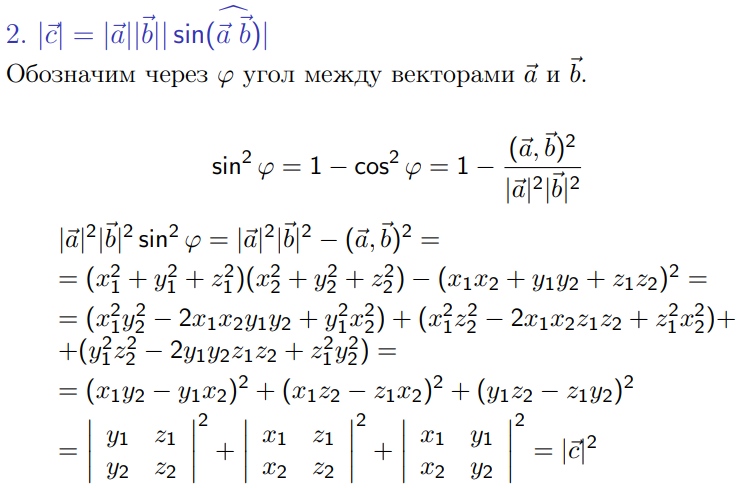
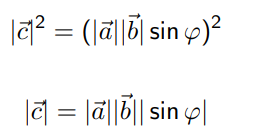
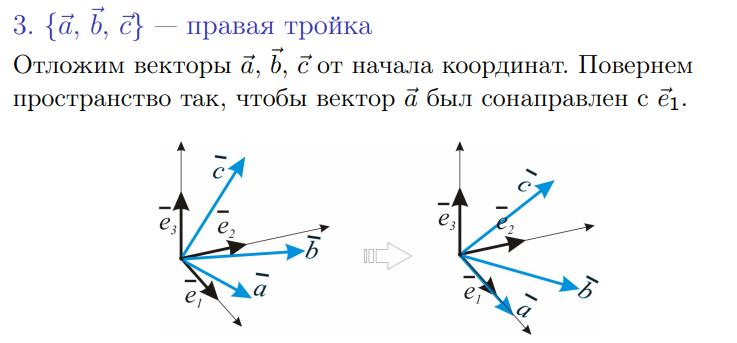
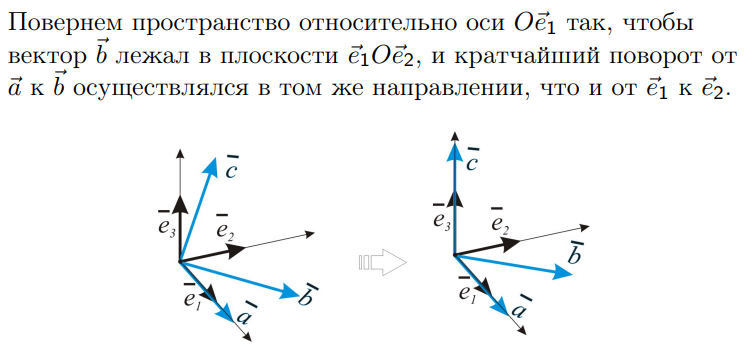
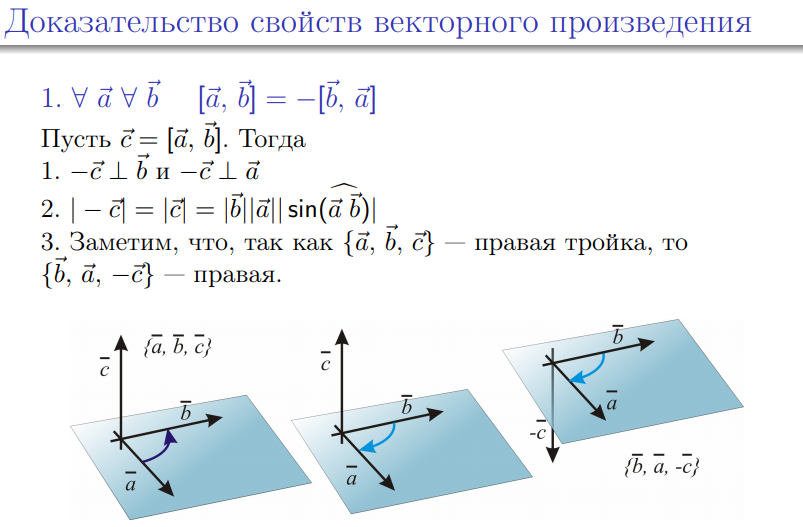
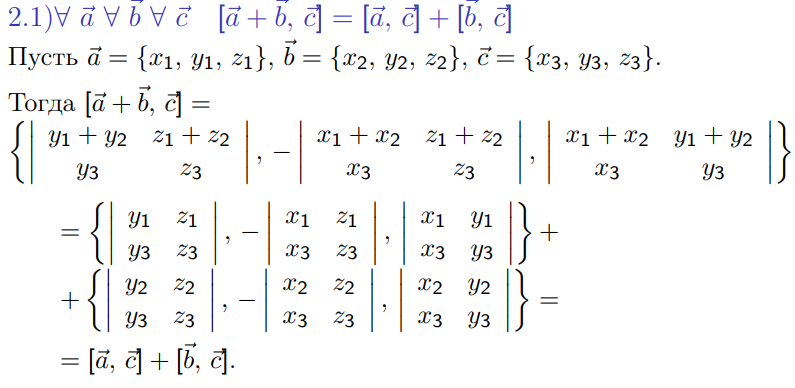
4 свойство – геометрический смысл векторного произведения.

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.