ПЛАН ЗАНЯТИЯ № 139. Тема занятия: Простейшие вероятностные задачи. Ход занятия

Стр 1 из 2Следующая ⇒

ПЛАН ЗАНЯТИЯ № 139

Тема занятия: Простейшие вероятностные задачи

Тип урока: комбинированный

Вид занятия: практикум

Цели:

– обучающая:познакомить с классическим определением вероятности, научить вычислять вероятности несложных событий;

– развивающая:способствовать развитию памяти, алгоритмического и логического мышления, внимания;

– воспитательная:продолжить воспитание чувства ответственности, самостоятельности, добросовестности.

Задачи:

- должен знать:классический и частотный подход к вычислению вероятности;

- должен уметь:вычислять вероятность события по классическому определению вероятности.

Обеспечение занятия:компьютер, мультимедийный проектор, экран, презентация, карточки с теоретическим материалом.

Внутридисциплинарные связи:

- Функции, непрерывность и пределы;

- Производная и ее приложения;

- Первообразная и интеграл;

- Математическая статистика;

- Уравнения, неравенства и системы.

Междисциплинарные связи: экономика, математическая статистика.

Методы обучения: проблемный, объяснительно – иллюстративный, частично-поисковый.

Ход занятия

1.1. Организация занятия(2–3 мин.)

Проверка присутствующих и готовности студентов к занятию.

Хочу знать, могу знать …

1.2. Сообщение темы и целей занятия(3 мин.)

1.3. Актуализация опорных знаний как переход к освоению новых знаний(7 мин.)

- Дайте понятие накопленных частостей.

- Объясните, как построить полигон вариационного ряда?

- Что такое гистограмма? Объясните способ её построения.

- Дайте определение среднего арифметического.

- Перечислите свойства среднего арифметического.

1.4. Контроль знаний(10 мин.)

Фронтальный опрос по основным понятиям математической статистики.

Решение упражнений № 50. 9, 50.10.

1.5. Сообщение и усвоение новых знаний(20 мин.)

Понятие испытания и события

Теория вероятностей и математическая статистика (ТВ и МС) относятся к числу прикладных математических дисциплин, поскольку она направлена на решение прикладных задач и возникла из чисто практических потребностей, а использует математические методы. В свою очередь двойное название дисциплины говорит о том, что в ней можно выделить два направления: ТВ и МС. Коротко можно сказать, что ТВ производит пересчет заданных вероятностей «простых» событий в вероятности «сложных» событий, а МС по наблюденным данным восстанавливает вероятности событий или проверяет, правы ли мы в своих предположениях относительно этих вероятностей.

Основная задача ТВ – изучение численных закономерностей в опытах, результаты которых не могут быть предсказаны однозначно до проведения испытаний. Первое необходимое условие, определяющее случайное событие, заключается в невозможности предсказания исхода некоторого действия.

Так мы не можем предсказать, какой стороной упадет подброшенная монета, сколько очков выпадет на игральной кости, сколько времени поработает электрическая лампочка, какое вещество образуется в результате определенной химической реакции, сколько частиц будет зарегистрировано счетчиком Гейгера-Мюллера за заданный промежуток времени, какой номер телефона у знакомого, какая погода будет 1 июня 2005 года и т.д.

Однако погодой до 1 июня 2005 года занимается метеорология, а после история.

Невозможность проведения испытания делает некорректным понятие случайного события в этом примере.

Итак, второе необходимое условие – возможность повторения испытания с первоначальным комплексом исходных данных, причем, хотя бы теоретические, бесконечное число раз.

Далее, выяснив номер телефона знакомого, сколько бы раз его ни спрашивали, новых цифр не добьешься. Определив исход химической реакции, и проведя ее заново при тех же условиях, нового вещества не получим. Отсюда вытекает условие – невозможность точного предсказания результатов не только первого испытания, но и каждого последующего.

Таким образом, случайными событиями являются опыты с подбрасыванием монеты, игральной кости, испытание лампочки и регистрация частиц. Невозможность точного предсказания результата конкретного испытания, говорит о том, что случайное событие характеризуется устойчивой частотой появления этого события. Например, стрелок, участвуя в данных соревнованиях, может попасть или не попасть в мишень. Однако в серии, например, из 100 выстрелов, проведенных в одних и тех же условиях (одна винтовка, то же расстояние, погода и т.д.), мы говорим о том, что в среднем у него 92 попадания (около 8 неудачных). Конечно, не в каждой сотне выстрелов 92 удачных, иногда их 90, иногда 91, или 93 или 94, иногда заметно меньше или больше 92, но вместе с тем, при многократном повторении опыта их будет 92.

Случайное явление можно охарактеризовать отношением числа его наступлений к числу его испытаний, в каждом из которых при одинаковых условиях всех испытаний оно могло наступить или не наступить.

Теория вероятностей есть раздел математики, в котором изучаются случайные явления и выявляются закономерности при массовом их повторении.

Всякое действие, явление, наблюдение с несколькими различными исходами, реализуемое при данном комплексе условий, будем называть испытанием. Например, многократное подбрасывание монеты, изготовление детали – испытания.

Результат этого действия – случайное событие. Например, появление цифры при подбрасывании монеты.

Равновозможные события – это события, которые имеют равные возможности произойти. Событие обозначают заглавными латинскими буквами: А, В, С, Д.

События называют несовместными, если никакие два из них не могут произойти в данном опыте вместе. В противном случае они называются совместными. (При подбрасывании монеты появление цифры исключает появление герба).

Достоверное – это событие, которое в данном испытании происходит обязательно (выигрыш про билету беспроигрышной лотереи). Достоверное событие обозначают U.

Событие называется невозможным, если оно в данном опыте не может произойти. (V). (При бросании игральной кости не возможно получить 7 очков).

Полной системой событий А₁, А₂, А₃, ... Ап называется совокупность несовместных событий, наступление хотя бы одного из которых обязательно при данном испытании. (Выпадение одного, двух, трех, четырех, пяти, шести очков игральной кости есть полная система событий).

Если полная система событий состоит из двух событий, то они называются противоположными и обозначаются А и .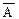

Пространство элементарных исходов (ПЭИ)

Рассмотрим простейший вариант случайного испытания – подбрасывание монеты. Если отвлечься от чисто гипотетических возможностей – падение монеты на ребро или вообще исчезновение ее, то возможны только два исхода: выпадение «герба» или «цифры». Эти два исхода в рамках данного опыта уже нельзя разбить на более мелкие составляющие, то есть они являются в некотором роде «элементарными». При бросании игральной кости такими неделимыми исходами являются: выпадение одного очка, двух и так далее, выпадение шести очков. Значит, имеется шесть элементарных исходов.

Падение идеальной (то есть не имеющей размеров) частицы на плоскость – это двумерный вектор в некоторой системе координат, имеет бесчисленное множество исходов.

Рассматривая все возможные исходы в данном опыте как множество W (омега) – мы получим ПЭИ или ПЭС.

Сами элементарные исходы обозначаются строчной буквой w (омега), снабжая ее индексами.

При решении задач ПЭИ можно описывать по-разному, но разумней подбирать наиболее простой вариант ПЭИ, необходимый для решения стоящей перед вами задачи.

Действия над событиями

В результате опыта может произойти один и только один элементарный исход w из ПЭИ W, тогда событие это произвольный набор ЭИ или произвольное подмножество множества элементарных исходов W.

Наглядное представление событий дает диаграмма Венна.

ПЭИ изображается прямоугольником, тогда каждый элементарный исход w соответствует точке внутри прямоугольника, а каждое событие А некоторой областью (рис. 1).

Само ПЭИ – событие достоверное, то есть оно выступает в двух качествах: в качестве собственно множества всех элементарных исходов и в качестве достоверного события.

Рис. 1

Пересечением (произведением) двух событий А и В называется событие С, происходящие тогда и только тогда, когда наступают оба события А и В, или, иными словами, состоящие и тех элементарных исходов, которые принадлежат и А и В (рис. 2).

Рис. 2

С = А Ç В или С = А·В = АВ.

Например, событие А – при подбрасывании двух монет, падение их одной стороной, событие В – выпадение хотя бы одного «герба».

А Ç В = С – выпадение двух «гербов».

Пример 2. А – выпадение четного числа очков при подбрасывании игральной кости, В – выпадение не менее трех очков. А Ç В = С – выпадение четырех или шести очков.

Если А Ç В = 0, то события А и В – не пресекаются или не совместимые (рис. 3).

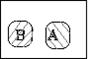
Рис. 3

Справедливы утверждения: АW = А; АÆ = Æ.

Пример 3. Событие А – выпадение четного числа очков при бросании игральной кости, событие В – выпадение нечетного числа очков. События А и В – несовместные.

Объединением (суммой) двух событий А и В называется событие С, происходящее тогда и только тогда, когда наступает хотя бы одно из событий А или В, то есть состоящее из тех элементарных исходов, которые принадлежат хотя бы одному из множеств А или В (рис. 4).

Рис. 4

С = А U B.

Пример 4.

Например, А – выпадение одного или трех очков при бросании игральной кости, событие В – три или пять очков. А U В = С – выпадение нечетного числа очков.

W U A = W; Æ U A = A.

В том случае, когда события А и В несовместны, употребляет наряду со знаком U, знак +. Знак + употребляют когда заведомо известно, что А и В несовместны и хотят это подчеркнуть.

Например: Æ U A = Æ + A = A

Разностью двух событий А и В называется событие С, происходящие тогда и только тогда, когда происходит событие А, но не происходит событие В, то есть состоящие из тех ЭИ, которые принадлежат А, но не принадлежат В (рис. 5).

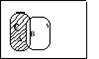
Рис. 5

Разность события А и В записывается в виде С = А/В.

Пример 5.

Событие А – выпадение хотя бы одного «герба» при подбрасывании двух монет, событие В – падение двух монет одной стороной. Разность С событий А и В представляет собой событие, заключающегося в выпадении ровно одного «герба».

Справедливы следующие формулы для разности двух событий, одно из которых достоверно или невозможно. A \ W = Æ, A \ Æ = А, Æ \ А = Æ. Кроме того, если А и В несовместны (АВ = Æ), то А \ В = А.

Физминутка(3 мин.)

1.6. Самостоятельная работа студентов в процессе усвоения новых знаний(15 мин.)

Задача

Имеется один билет лотереи «6 из 45». Событие А – билет выигрышный, событие В – билет невыигрышный. Являются ли события А и В несовместными? (Да).

Задача

В коробке находятся 30 пронумерованных шаров. Установить, какие из следующих событий являются невозможными, достоверными, противоположными:

А – достали пронумерованный шар,

В – шар с четным номером,

С – шар с нечетным номером,

Д – шар без номера.

Какие из них образуют полную группу?

А – достоверное, Д – невозможное, В и С – противоположные. А и Д; В и С – образуют полную группу.

12 Следующая ⇒