
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Работа определяется только расстояниями от источника до начальной и конечной точки траектории. Такое силовое поле в механике мы называли потенциальным.
1 вопрос
Фи́зика (от др.-греч. φύσις — природа) — область естествознания, наука, изучающая наиболее общие и фундаментальные закономерности, определяющие структуру и эволюцию материального мира. Законы физики лежат в основе всего естествознания
Предмет физики
Физика — это наука о природе в самом общем смысле (часть природоведения). Она изучает материю (вещество и поля) и наиболее простые и вместе с тем наиболее общие формы её движения, а также фундаментальные взаимодействия природы, управляющие движением материи.
Некоторые закономерности являются общими для всех материальных систем, например, сохранение энергии, — их называют физическими законами. Физику иногда называют «фундаментальной наукой», поскольку другие естественные науки (биология, геология, химия и др.) описывают только некоторый класс материальных систем, подчиняющихся законам физики. Например, химия изучает атомы, образованные из них вещества и превращения одного вещества в другое. Химические же свойства вещества однозначно определяются физическими свойствами атомов и молекул, описываемыми в таких разделах физики, как термодинамика, электромагнетизм и квантовая физика.
Физика тесно связана с математикой: математика предоставляет аппарат, с помощью которого физические законы могут быть точно сформулированы. Физические теории почти всегда формулируются в виде математических выражений, причём используются более сложные разделы математики, чем обычно в других науках. И наоборот, развитие многих областей математики стимулировалось потребностями физических теорий
В основе своей физика — экспериментальная наука: все её законы и теории основываются и опираются на опытные данные. Однако зачастую именно новые теории являются причиной проведения экспериментов и, как результат, лежат в основе новых открытий. Поэтому принято различать экспериментальную и теоретическую физику.
Экспериментальная физика исследует явления природы в заранее подготовленных условиях. В её задачи входит обнаружение ранее неизвестных явлений, подтверждение или опровержение физических теорий. Многие достижения в физике были сделаны благодаря экспериментальному обнаружению явлений, не описываемых существующими теориями. Например, экспериментальное изучение фотоэффекта послужило одной из посылок к созданию квантовой механики (хотя рождением квантовой механики считается появление гипотезы Планка, выдвинутой им для разрешения ультрафиолетовой катастрофы — парадокса классической теоретической физики излучения).
В задачи теоретической физики входит формулирование общих законов природы и объяснение на основе этих законов различных явлений, а также предсказание до сих пор неизвестных явлений. Верность любой физической теории проверяется экспериментально: если результаты эксперимента совпадают с предсказаниями теории, она считается адекватной (достаточно точно описывающей данное явление).
При изучении любого явления экспериментальные и теоретические аспекты одинаково важны.
В современном мире значение физики чрезвычайно велико. Всё то, чем отличается современное общество от общества прошлых веков, появилось в результате применения на практике физических открытий. Так, исследования в области электромагнетизма привели к появлению телефонов, открытия в термодинамике позволили создать автомобиль, развитие электроники привело к появлению компьютеров.
Физическое понимание процессов, происходящих в природе, постоянно развивается. Большинство новых открытий вскоре получают применение в технике и промышленности. Однако новые исследования постоянно поднимают новые загадки и обнаруживают явления, для объяснения которых требуются новые физические теории. Несмотря на огромный объём накопленных знаний, современная физика ещё очень далека от того, чтобы объяснить все явления природы.
Общенаучные основы физических методов разрабатываются в теории познания и методологии науки.
| 2 вопрос Состояние системы – это реализация при данных условиях отдельных потенциальных возможностей системы. Оно характеризуется набором величин, которые могут быть измерены наблюдателем. Система– это совокупность элементов множества любой природы. Число независимых функций, с помощью которых можно описать поведение системы, называется числом степеней свободы этой системы. Система отсчета – это совокупность тела отсчета и часов, связанных с этим телом, по отношению к которому изучается движение. Под механическим движением понимают изменение с течением времени взаимного положения тел или их частиц в пространстве. Пространство – это форма существования материи, выражающая порядок сосуществования отдельных объектов. Перемещение - это вектор, по модулю равный расстоянию между начальной и конечной точкой, и направленный от начальной точки к конечной. Средняя скорость - это векторная величина, равная отношению перемещения Δr ко времени Δt, в течение которого это перемещение совершено. . Мгновенная скорость - это предельное значение средней скорости vср при Δt, стремящемся к нулю. В классической механике состояние системы в каждый момент времени определяется заданием координат и скоростей. Опыт показывает, что задание координат и скоростей в начальный момент времени позволяет определить координаты и скорости системы в любой последующий момент времени. Для этого достаточно решить одно или систему уравнений движения при заданных значениях координат и скоростей в начальный момент времени. В силу однозначности движения число уравнений движения должно совпадать с числом координат и скоростей системы. Число независимых координат и скоростей системы, в общем случае функций времени, должно быть равно числу степеней свободы системы. Существует множество способов задания уравнений движения. | 3 вопрос
Тангенциа́льное ускоре́ние — компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости. Равно произведению единичного вектора, направленного по скорости движения, на производную модуля скорости по времени. Таким образом, направлено в ту же сторону, что и вектор скорости при ускоренном движении (положительная производная) и в противоположную при замедленном (отрицательная производная). Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени: 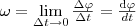 Вектор ω направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dφ (рис. 2). Размерность угловой скорости dim ω = Т-1, а ее единица — радиан в секунду (рад/с). Линейная скорость точки (см. рис. 1) Вектор ω направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dφ (рис. 2). Размерность угловой скорости dim ω = Т-1, а ее единица — радиан в секунду (рад/с). Линейная скорость точки (см. рис. 1) 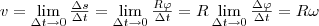 т.е
v=ωR
т.е
v=ωR
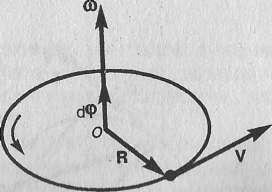 Рис.2
Угловым ускорением называется векторная величина, равная первой производной yгловой скорости по времени:
Рис.2
Угловым ускорением называется векторная величина, равная первой производной yгловой скорости по времени: 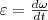 Тангенциальная составляющая ускорения aτ=dv/dt , v = ωR и Тангенциальная составляющая ускорения aτ=dv/dt , v = ωR и 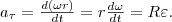 Нормальная составляющая ускорения Нормальная составляющая ускорения 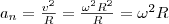 s = Rφ, v = Rω, аτ = R?, an = ω2R.
s = Rφ, v = Rω, аτ = R?, an = ω2R.
|
4 вопрос
ДИНАМИКА, часть кинетики - раздела теоретической механики, в котором рассматриваются тела в условиях воздействия на них заданных сил.
СИЛА - физическое воздействие, приводящее или стремящееся привести к изменению состояния покоя или движения материального тела.
Материальная точка - идеализированная модель физического тела, размерами, структурой и формой которого можно пренебречь при решении поставленной задачи.
МАССА- мера инерционных и гравитационных свойств материальной точки.
Механическая система - совокупность материальных точек:
- движущихся согласно законам классической механики; и
- взаимодействующих друг с другом и с телами, не включенными в эту совокупность.
Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени.
Второй закон Ньютона - основной закон динамики поступательного движения - отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил. Рассмотривая действие различных сил на данную материальную точку (тело), то ускорение, приобретаемое телом, всегда прямо пропорционально равнодействующей данных приложенных сил: 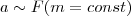 (1) При действии одинаковой силы на тела с различными массами ускорения тел оказываются различными, а именно (1) При действии одинаковой силы на тела с различными массами ускорения тел оказываются различными, а именно 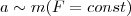 (2) Учитывая (1) и (2) и то, что сила и ускорение - величины векторные, можем записать (2) Учитывая (1) и (2) и то, что сила и ускорение - величины векторные, можем записать 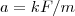 (3) (3)
|
5 вопрос
Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.
В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.
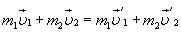 Центр масс— воображаемая точка С, положение которой характеризует распределение масс этой системы.
Закон движения центра масс— в инерциальных системах отсчёта центр масс системы движется как материальная точка, в которой находится масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему.
Центр масс— воображаемая точка С, положение которой характеризует распределение масс этой системы.
Закон движения центра масс— в инерциальных системах отсчёта центр масс системы движется как материальная точка, в которой находится масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему.
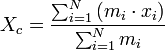 ; ; 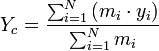 ; ; 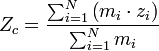 Система центра масс — система отсчёта, относительно которой центр масс механической системы неподвижен.
Система центра масс — система отсчёта, относительно которой центр масс механической системы неподвижен.
|
6 вопрос
Выведем уравнение движения тела переменной массы на примере движения ракеты. Если с момент времени t масса ракеты m, а ее скорость V,то по истечении времени dt ее масса уменьшится на dm и станет равной m-dm, а скорость станет равной V+dV. Изменение импульса системы за отрезок времени dt
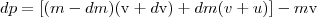 Тогда
Dp=mdV+Udm.
Если на систему действуют внешние силы, то dp=Fdt
Мы получили уравнение движения тела переменной массы
ma=F+Fр. , которое впервые было выведено И.Б.Мещерским
V=U ln m0/m - это соотношение называется формулой Циолковского.
Она показывает, что:1) чем больше конечная масса, тем больше должна быть стартовая масса ракеты. 2) чем больше скорость истечения газов, тем больше может быть конечная масса при данной стартовой массе ракеты(U)
Тогда
Dp=mdV+Udm.
Если на систему действуют внешние силы, то dp=Fdt
Мы получили уравнение движения тела переменной массы
ma=F+Fр. , которое впервые было выведено И.Б.Мещерским
V=U ln m0/m - это соотношение называется формулой Циолковского.
Она показывает, что:1) чем больше конечная масса, тем больше должна быть стартовая масса ракеты. 2) чем больше скорость истечения газов, тем больше может быть конечная масса при данной стартовой массе ракеты(U)
| 7 вопрос
Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П0 и П , одна из которых неподвижна, а другая жестко связана с телом.
φ=φ(t) – уравнение вращательного движения твердого тела.
Момент инерции- физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:
I=m*R^2( полый тонкостенный цилиндр)
I=1/2m*R^2(сплошной цилиндр)
I=1/12m*l^2( прямой тонкий стержень,ось перпендикулярна стержню и проходит через середину)
I=1/3m*l^2(прям. Тонкий стержень, ось перепндик. И проходит через конец)
I=2/5m*R^2(шар. Ось проходит через центр)
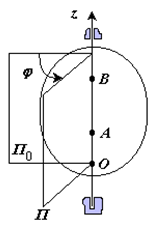 Рис. 1.3
За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.
Теоре́маГю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математикаЯкоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции тела
Рис. 1.3
За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.
Теоре́маГю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математикаЯкоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции тела 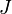 относительно произвольной оси равен сумме момента инерции этого тела относительно произвольной оси равен сумме момента инерции этого тела 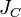 относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела 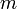 на квадрат расстояния на квадрат расстояния 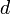 между осями: между осями:
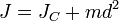 где
где
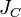 — известный момент инерции относительно оси, проходящей через центр масс тела, — известный момент инерции относительно оси, проходящей через центр масс тела,
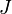 — искомый момент инерции относительно параллельной оси, — искомый момент инерции относительно параллельной оси,
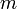 — масса тела, — масса тела,
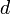 — расстояние между указанными осями. — расстояние между указанными осями.
|
8 вопрос
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.
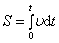
| 9 вопрос

|
| 10 вопрос Гироско́п — устройство, способное реагировать на изменение угловориентации связанного с ним тела относительно инерциальной системы координат, как правило, основанное на законе сохранения вращательного момента (момента импульса). Термин впервые введен Жаном (Бернаром Леоном) Фуко в его докладе в 1852 году Французской Академии Наук. Доклад был посвящён способам экспериментального обнаружения вращения Земли в инерциальном пространстве. Этим обусловлено и название «гироскоп» Гироскопический эффект - это удержание (устойчивость) оси вращения объекта в пространстве. Этот эффект зависит от массы объекта, угловой скорости и от распределения моментов инерции. Если моменты инерции распределены немного неравномерно, то от этого будут возникать эффекты прецессии и нутации. Если моменты инерции распределены неравномерно, при этом ещё масса и угловая скорость объекта небольшие, тогда при эффекте прецессии ось объекта сначала описывает небольшую окружность, диаметр который всё время увеличивается. Затем ось объекта сама начинается вращаться в произвольных направлениях (кувыркаться). | 11 вопрос
Энергия - общая мера различных форм движения материи. Для количественной характеристики качественно различающихся форм движения и соответствующих им взаимодействий вводят различные виды энергии: механическую, внутреннюю, гравитационную, электромагнитную, ядерную и т.д… Исходя из того, что любой материальный объект всегда находится в движении (находятся в движении определяющие его характеристики), что отражено в формулах 1 - 6 предыдущей главы установкой векторов, непротиворечивым шагом будет представление объекта в следующей математической форме: 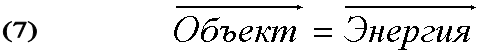 Т.е. согласуя проведенные ранее рассуждения с существующими определениями энергии, получаем полное и очевидное право поставить между понятиями объекта и энергии знак равенства. Для того, чтобы это право "ущемить", необходимо найти материальный объект, находящийся вне движения. По утверждениям главы 1 такого объекта в природе не существует. Кроме того, если взглянуть на определение энергии немного шире, то можно увидеть, что любая энергия представляет собой переход или возможность перехода объекта из одного состояния в другое путем взаимодействия с другим объектом. Описание и конкретное исследование любого вида энергии - это всего лишь оценка количественных и качественных изменений взаимодействующих объектов при их переходе (или при возможности перехода) в некоторое другое состояние. Согласуясь с результатами предыдущих рассуждений несложно заметить сходство поведения энергии с поведением того, что было определено, как объективная информация.
В физике механи́ческаяэне́ргия описывает сумму потенциальной и кинетической энергии, имеющихся в компонентах механической системы. Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу Т.е. согласуя проведенные ранее рассуждения с существующими определениями энергии, получаем полное и очевидное право поставить между понятиями объекта и энергии знак равенства. Для того, чтобы это право "ущемить", необходимо найти материальный объект, находящийся вне движения. По утверждениям главы 1 такого объекта в природе не существует. Кроме того, если взглянуть на определение энергии немного шире, то можно увидеть, что любая энергия представляет собой переход или возможность перехода объекта из одного состояния в другое путем взаимодействия с другим объектом. Описание и конкретное исследование любого вида энергии - это всего лишь оценка количественных и качественных изменений взаимодействующих объектов при их переходе (или при возможности перехода) в некоторое другое состояние. Согласуясь с результатами предыдущих рассуждений несложно заметить сходство поведения энергии с поведением того, что было определено, как объективная информация.
В физике механи́ческаяэне́ргия описывает сумму потенциальной и кинетической энергии, имеющихся в компонентах механической системы. Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу
|
12 вопрос
Потенциальная энергия — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил.
Потенциальная энергия 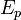 в поле тяготения Земли вблизи поверхности приближённо выражается формулой: в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
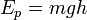 Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.
В физике консервати́вныеси́лы— силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.
Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется. Полная механическая энергия системы – сумма ее кинетической и потенциальной энергии.
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.
Ek1 + Ep1 = Ek2 + Ep2.
Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.
В физике консервати́вныеси́лы— силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.
Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется. Полная механическая энергия системы – сумма ее кинетической и потенциальной энергии.
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.
Ek1 + Ep1 = Ek2 + Ep2.
| 13 вопрос
Изменение механического движения тела вызывается силами , действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы.
Мо́щность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени. Различают среднюю мощность за промежуток времени 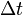 : :
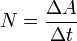 и мгновенную мощность в данный момент времени:
и мгновенную мощность в данный момент времени:
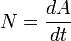 Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.
Основные кинематические характеристики вращательного движения тела — его угловая скорость (
Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.
Основные кинематические характеристики вращательного движения тела — его угловая скорость ( 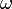 ) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z: ) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:
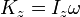 и кинетическая энергия
и кинетическая энергия
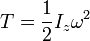
|
| 14 вопрос Преобразова́ния Галиле́я — в классической механике (механике Ньютона) преобразования координат и времени при переходе от одной инерциальной системы отсчета (ИСО) к другой.. Преобразования Галилея подразумевают одинаковость времени во всех системах отсчета и выполнение принципа относительности (Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в пустоте и в ограниченном объёме пространства. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе, преобразования Галилея приближенно верны с очень большой точностью. Принцип относительности Галилея Из формулы для ускорений следует, что если движущаяся система отсчета движется относительно первой без ускорения, то есть , то ускорение тела относительно обеих систем отсчета одинаково. Поскольку в Ньютоновской динамике из кинематических величин именно ускорение играет роль, то, если довольно естественно предположить, что силы зависят лишь от относительного положения и скоростей физических тел, окажется, что все уравнения механики запишутся одинаково в любой инерциальной системе отсчета — иначе говоря, законы механики не зависят от того, в какой из инерциальных систем отсчета мы их исследуем, не зависят от выбора в качестве рабочей какой-то конкретной из инерциальных систем отсчета. Также — поэтому — не зависит от такого выбора системы отсчета наблюдаемое движение тел (учитывая, конечно, начальные скорости). Это утверждение известно как принцип относительности Галилея, в отличие от Принципа относительности Эйнштейна Иным образом этот принцип формулируется (следуя Галилею) так: если в двух замкнутых лабораториях, одна из которых равномерно прямолинейно (и поступательно) движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым. | 15 вопрос
Специальная теория относительности (СТО; также частная теория относительности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей называется общей теорией относительности.
Описываемые специальной теорией относительности отклонения в протекании физических процессов от предсказаний классической механики называют релятивистскими эффектами, а скорости, при которых такие эффекты становятся существенными, — релятивистскими скоростями.
Преобразованиями Лоренца в физике, в частности, в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно-временные координаты каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой.
Пусть координатные оси двух инерциальных систем отсчёта S и S' параллельны друг другу, (t, x,y, z) — время и координаты некоторого события, наблюдаемого относительно системы S, а (t',x',y',z') — время и координаты того же события относительно системы S'. Если система S' движется равномерно и прямолинейно со скоростью v относительно S, то справедливы преобразования Лоренца:
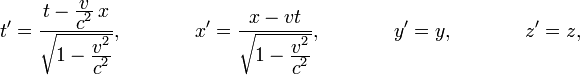
|
16 вопрос
В СТО постулируется возможность определения единого времени в рамках данной инерциальной системы отсчёта. Для этого вводится процедура синхронизации двух часов, находящихся в различных точках ИСО. Пусть от первых часов, в момент времени 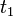 ко вторым посылается сигнал (не обязательно световой) с постоянной скоростью ко вторым посылается сигнал (не обязательно световой) с постоянной скоростью 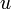 . Сразу по достижении вторых часов (по их показаниям в момент времени . Сразу по достижении вторых часов (по их показаниям в момент времени 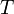 ) сигнал отправляется обратно с той же постоянной скоростью ) сигнал отправляется обратно с той же постоянной скоростью 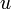 и достигает первых часов в момент времени и достигает первых часов в момент времени 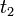 . Часы считаются синхронизированными, если выполняется соотношение . Часы считаются синхронизированными, если выполняется соотношение 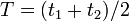 .
Предполагается, что такая процедура в данной инерциальной системе отсчёта может быть проведена для любых неподвижных относительно друг друга часов, так что справедливо свойство транзитивности: если часы A синхронизованы с часами B, а часы B синхронизованы с часами C, то часы A и C также окажутся синхронизованными.
В отличие от классической механики единое время можно ввести только в рамках данной системы отсчёта. В СТО не предполагается, что время является общим для различных систем. В этом состоит основное отличие аксиоматики СТО от классической механики, в которой постулируется существование единого (абсолютного) времени для всех систем отсчёта.
Пространство в инерциальных системах отсчёта предполагается изотропным (нет выделенных направлений). Это приводит к тому, что .
Предполагается, что такая процедура в данной инерциальной системе отсчёта может быть проведена для любых неподвижных относительно друг друга часов, так что справедливо свойство транзитивности: если часы A синхронизованы с часами B, а часы B синхронизованы с часами C, то часы A и C также окажутся синхронизованными.
В отличие от классической механики единое время можно ввести только в рамках данной системы отсчёта. В СТО не предполагается, что время является общим для различных систем. В этом состоит основное отличие аксиоматики СТО от классической механики, в которой постулируется существование единого (абсолютного) времени для всех систем отсчёта.
Пространство в инерциальных системах отсчёта предполагается изотропным (нет выделенных направлений). Это приводит к тому, что 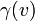 является чётной функцией скорости: является чётной функцией скорости: 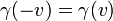 .
Рассмотрим, например, измерение длины некоторого объекта (линейки), неподвижного в системе отсчёта S'. Если одновременно .
Рассмотрим, например, измерение длины некоторого объекта (линейки), неподвижного в системе отсчёта S'. Если одновременно 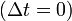 в системе S измерить координаты «начала» и «конца» линейки, то её длина в системе S измерить координаты «начала» и «конца» линейки, то её длина 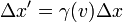 не должна зависеть от направления (знака) скорости не должна зависеть от направления (знака) скорости 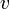 , откуда следует, что функция , откуда следует, что функция 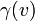 является чётной. является чётной.
| 17 вопрос Релятивистская динамика свободной частицы определяется полностью поведением ее вектора состояния при преобразованиях g квантово-механической группы Пуанкаре - Знание явного вида оператора U ( g), действующего на вектор состояния частицы, равносильно решению уравнения движения для свободной частицы. В релятивистской динамике теория, связанная со свободной частицей, не тривиальна, ибо она служит для того, чтобы связать физические понятия и математическую схему. В релятивистской динамике, как и в ньютоновской, принимается, что импульс р материальной точки пропорционален ее массе т и совпадает по направлению со скоростью v этой точки. Основное уравнение релятивистской динамики позволяет найти закон действующей на частицу силы F, если известна зависимость от времени релятивистского импульса p ( t), а с другой стороны, найти уравнение движения частицы r ( t), если известны действующая сила и начальные условия - скорость VQ и положение TO частицы в начальный момент времени. С помощью релятивистской динамики можно, исходя из данного состояния в любой момент времени, построить новое состояние, соответствующее новому моменту времени. Однако в релятивистской динамике уравнением движения является уравнение, которое инвариантно относительно преобразований Лоренца по определению, а сила F не инвариантна. К сожалению, релятивистская динамика вносит в это заключение свою поправку. Но эта масса неограниченно растет при приближении скорости движения к световой; соответственно увеличивается и продолжительность полуоборота. Следовательно, при постоянстве частоты генератора нарушается необходимое условие ускорения частицы - синхронизм между ее вращением и переменами полярности электродов. |
18 вопрос
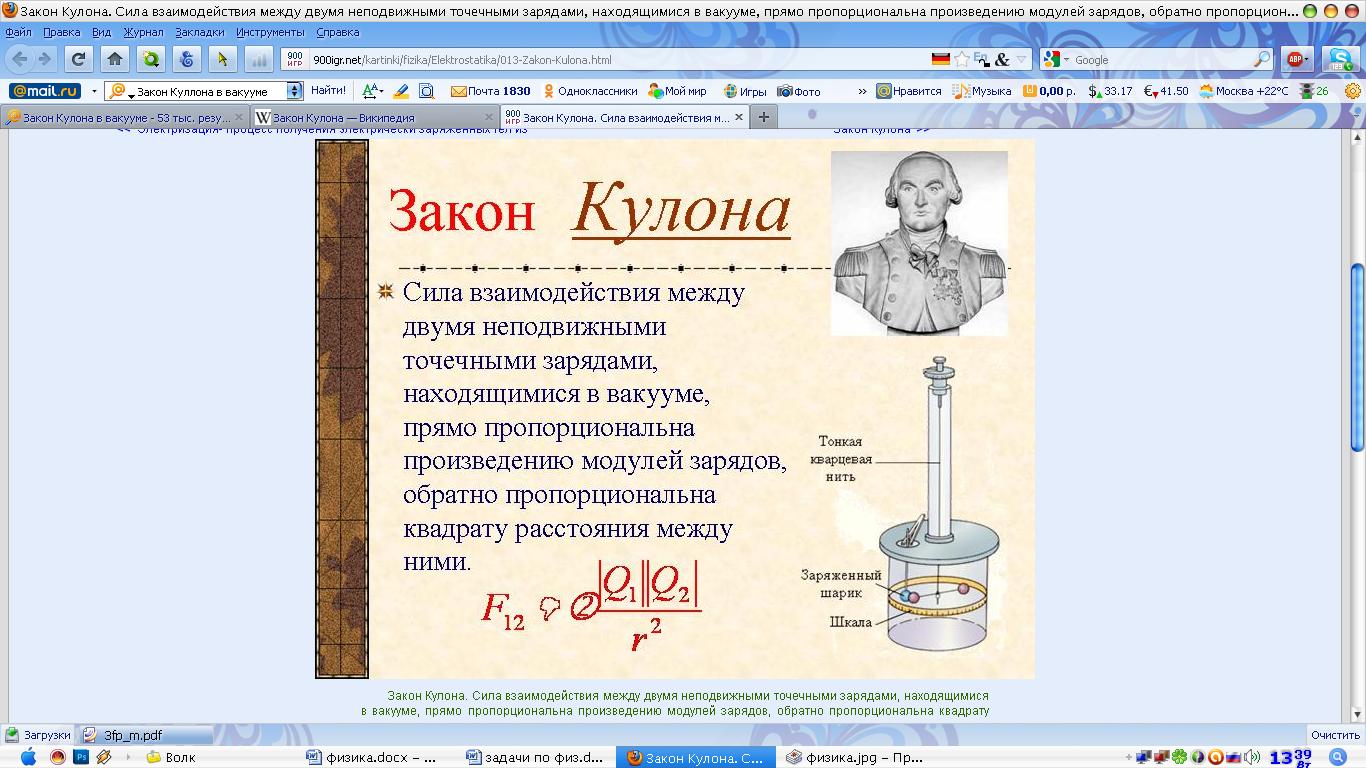
Электри́ческий заря́д — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии. Впервые электрический заряд был введён в законе Кулона в 1785 году.
Единица измерения заряда в СИ — кулон — электрический заряд, проходящий через поперечное сечение проводника при силе тока 1 А за время 1 с. Заряд в один кулон очень велик. Если бы два носителя заряда (q1 = q2 = 1 Кл) расположили в вакууме на расстоянии 1 м, то они взаимодействовали бы с силой 9·109 H.
Электрический заряд дискретен, то есть заряд любого тела составляет целое кратное от элементарного электрического заряда
Электрический заряд замкнутой системы[5] сохраняется во времени и квантуется — изменяется порциями, кратными элементарному электрическому заряду, то есть, другими словами, алгебраическая сумма электрических зарядов тел или частиц, образующих электрически изолированную систему, не изменяется при любых процессах, происходящих в этой системе.
Закон сохранения заряда— один из основополагающих законов физики. Закон сохранения заряда был впервые экспериментально подтверждён в 1843 году великим английским ученым Майклом Фарадеем и считается на настоящее время одним из фундаментальных законов сохранения в физике (подобно законам сохранения импульса и энергии). Всё более чувствительные экспериментальные проверки закона сохранения заряда, продолжающиеся и поныне, пока не выявили отклонений от этого закона.
Закон Кулона
| 19 вопрос
Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы 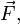 действующей на неподвижный[1] пробный заряд, помещенный в данную точку поля, к величине этого заряда действующей на неподвижный[1] пробный заряд, помещенный в данную точку поля, к величине этого заряда 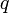 : :
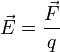 .
Напряжённость электрического поля в СИ измеряется в вольтах на метр [В/м] или в ньютонах на кулон.
При́нцип суперпози́ции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:
результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.
Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.
Поток напряженности электрического поля, проходящий через замкнутую поверхность, пропорционален суммарному электрическому заряду, содержащемуся внутри этой поверхности. .
Напряжённость электрического поля в СИ измеряется в вольтах на метр [В/м] или в ньютонах на кулон.
При́нцип суперпози́ции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:
результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.
Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.
Поток напряженности электрического поля, проходящий через замкнутую поверхность, пропорционален суммарному электрическому заряду, содержащемуся внутри этой поверхности.
|
20 вопрос
Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Применяется отдельно для вычисления электростатических полей.
Теорема Гаусса для напряжённости электрического поля в вакууме
Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.
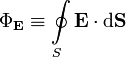 — поток вектора напряжённости электрического поля через замкнутую поверхность — поток вектора напряжённости электрического поля через замкнутую поверхность 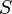 .
Теорема Гаусса может быть доказана как теорема в электростатике исходя из закона Кулона. Формула однако также верна в электродинамике, хотя в ней она чаще всего не выступает в качестве доказываемой теоремы, а выступает в качестве постулируемого уравнения. .
Теорема Гаусса может быть доказана как теорема в электростатике исходя из закона Кулона. Формула однако также верна в электродинамике, хотя в ней она чаще всего не выступает в качестве доказываемой теоремы, а выступает в качестве постулируемого уравнения.
| 21 вопрос
Применение теоремы Гаусса
Являясь (вкупе с уравнением о нулевой циркуляции электрического поля) основным полевым уравнением электростатики (вместе эти два уравнения в дифференциальной форме эквивалентны уравнению Пуассона — основному и единственному дифференциальному уравнению классической теории для электростатического потенциала.
В электродинамике теорема Гаусса (закон Гаусса) также остается (полностью в том же виде) одним из главных уравнений — одним из четырех уравнений Максвелла.
В некоторых ситуациях теорема Гаусса может быть использована для прямого и легкого вычисления электростатического поля непосредственно. Это ситуации, когда симметрия задачи позволяет наложить на напряженность электрического поля такие дополнительные условия, что вместе с теоремой Гаусса этого хватает для прямого элементарного вычисления (без применения двух обычных общих способов — решения уравнения в частных производных или лобового интегрирования кулоновских полей для элементарных точечных зарядов).
Расчет напряженности поля сферически симметричного распределения заряда
Способ расчета с помощью теоремы Гаусса для любого сферически симметричного распределения заряда в целом сводится к тому, что описано выше для случая точечного заряда (см. параграф о законе Кулона).
Отметим тут только в отношении неточечных источников обладающих сферической симметрией вот что (всё это является очевидными следствиями применения описанного там метода):
Сферически симметричный заряд с концентрической сферической пустотой (или незаряженной областью) в середине, не создает внутри этой пустоты поля (напряженность поля там равна нулю).
Вообще поле на расстоянии r от центра создается только теми зарядами, которые находятся глубже к центру. Это поле можно рассчитать по закону Кулона: 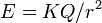 , только под Q здесь следует понимать суммарный заряд шаровой области радиусом r (а это означает, что зависимость от r в итоге отличается от кулоновской, поскольку с ростом r растет Q, по карйней мере пока r не больше радиуса всей заряженной области — если только она в свою очередь конечна). , только под Q здесь следует понимать суммарный заряд шаровой области радиусом r (а это означает, что зависимость от r в итоге отличается от кулоновской, поскольку с ростом r растет Q, по карйней мере пока r не больше радиуса всей заряженной области — если только она в свою очередь конечна).
|
22 вопрос
Работа электростатического поля (A)
A = Fd=qEd,
A1 = Fd1 cos , но d1 cos = d, A1 = qEd |
Работа определяется только расстояниями от источника до начальной и конечной точки траектории. Такое силовое поле в механике мы называли потенциальным.
Существуют два равнозначных определения консервативной силы. Оба они подробно обсуждались в механике.
Консервативной называется сила, работа которой не зависит от формы траектории.
Консервативной называется сила, работа которой на замкнутой траектории равна нулю.
Рассмотрим перемещение заряда q в электростатическом поле 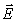 по замкнутой траектории (рис. 3.5.). Заряд из точки 1 перемещается по пути L1 в точку 2, а затем возвращается в исходное положение по другому пути L2. В процессе этого движения на заряд со стороны поля действует консервативная электрическая сила:
по замкнутой траектории (рис. 3.5.). Заряд из точки 1 перемещается по пути L1 в точку 2, а затем возвращается в исходное положение по другому пути L2. В процессе этого движения на заряд со стороны поля действует консервативная электрическая сила:
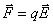 .
.
Работа этой силы на замкнутой траектории L = L1 + L2 равна нулю:
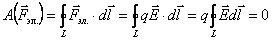 .
.
Это уравнение, упростив, запишем так:
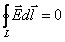
Теорема о циркуляции в электростатике: циркуляция вектора напряжённости электростатического поля по любому замкнутому контуру равна нулю.
| A = FS cos |
если = 90 , то A = 0
1 = 2 = 3 = 4
Силовые линии перпендикулярны такой поверхности .
Разность потенциалов — это скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к этому заряду.
В СИ единицей разности потенциалов является вольт (В).
1 В — разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа в 1 Дж.
Разность потенциалов в отличие от потенциала не зависит от выбора нулевой точки. Разность потенциалов φ1 - φ2 часто называют электрическим напряжением между данными точками
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|