
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Качественные задачи
Качественные задачи
1.В цилиндрическом сосуде под поршнем длительное время находятся вода и ее пар. Поршень начинают выдвигать из сосуда. При этом температура воды и пара остается неизменной. Как будет меняться при этом масса жидкости в сосуде? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.
Ответ:
| Образец возможного решения |
| 1) Ответ: масса жидкости в сосуде будет уменьшаться. 2) Вода и водяной пар находятся в закрытом сосуде длительное время, поэтому водяной пар является насыщенным. 3) При выдвигании поршня происходит изотермическое расширение пара, давление и плотность насыщенного пара в этом процессе не меняются. Следовательно, будет происходить испарение жидкости. Значит, масса жидкости в сосуде будет уменьшаться. |
2.Мягкая пружина из нескольких крупных витков провода подвешена к потолку.  Верхний конец пружины подключается к источнику тока через ключ К, а нижний – с помощью достаточно длинного мягкого провода (см. рисунок). Как изменится длина пружины через достаточно большое время после замыкании ключа К? Тепловым расширением пренебречь. Ответ поясните, указав, какие физические явления и закономерности вы использовали для объяснения.
Верхний конец пружины подключается к источнику тока через ключ К, а нижний – с помощью достаточно длинного мягкого провода (см. рисунок). Как изменится длина пружины через достаточно большое время после замыкании ключа К? Тепловым расширением пренебречь. Ответ поясните, указав, какие физические явления и закономерности вы использовали для объяснения.
| Образец возможного решения |
| 1) Пружина сожмется, её длина уменьшится. 2) До замыкания ключа пружина находится в состоянии равновесия, в котором упругие силы, действующие на каждый виток пружины со стороны соседних витков, уравновешивают силу тяжести, действующую на виток. 3) При замыкании ключа К по цепи пойдет ток. В соседних витках пружины токи потекут сонаправленно. Проводники с сонаправленными токами притягиваются друг к другу. В результате будет достигнуто новое состояние равновесия (пружина станет короче), в котором упругие силы, действующие на каждый виток пружины со стороны соседних витков, будут уравновешивать силу тяжести и силу Ампера, действующие на виток. |
3. 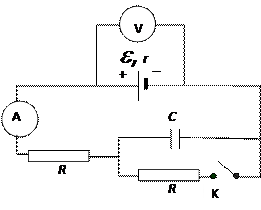 На рисунке показана электрическая цепь, содержащая источник тока (с внутренним сопротивлением), два резистора, конденсатор, ключ К, а также амперметр и идеальный вольтметр. Как изменятся показания амперметра и вольтметра в результате замыкания ключа К? Ответ поясните, указав, какие физические явления и закономерности вы использовали для объяснения.
На рисунке показана электрическая цепь, содержащая источник тока (с внутренним сопротивлением), два резистора, конденсатор, ключ К, а также амперметр и идеальный вольтметр. Как изменятся показания амперметра и вольтметра в результате замыкания ключа К? Ответ поясните, указав, какие физические явления и закономерности вы использовали для объяснения.
| Образец возможного решения |
1) Показания амперметра станут отличными от нуля, а показания вольтметра уменьшатся.
2) До замыкания ключа амперметр и вольтметр показывают, соответственно, нулевой ток и ЭДС источника.
3) Замыкание ключа вызовет появление тока в цепи, поэтому показания вольтметра уменьшатся на величину падения напряжения на внутреннем сопротивлении источника. По закону Ома для полной цепи 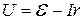 . .
|
4. На фотографии изображена электрическая цепь, состоящая из резистора, реостата, ключа, цифровых вольтметра, подключенного к батарее, и амперметра.
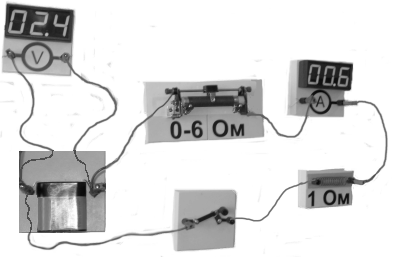
Составьте принципиальную электрическую схему этой цепи, и, используя законы постоянного тока, объясните, как изменятся (увеличится или уменьшится) сила тока в цепи и напряжение на батарее при перемещении движка реостата в крайнее правое положение.
Ответ:
| Образец возможного решения (рисунок обязателен) | |
| 1. Эквивалентная электрическая схема цепи, учитывающая внутреннее сопротивление батареи, изображена на рисунке, где I – сила тока в цепи. Ток через вольтметр практически | 
|
| не течет, а сопротивление амперметра пренебрежимо мало. 2. Сила тока в цепи определяется законом Ома для замкнутой (полной) цепи: В соответствии с законом Ома для участка цепи напряжение, измеряемое вольтметром: 3. При перемещении движка реостата вправо его сопротивление уменьшается, что приводит к уменьшению полного сопротивления цепи. Сила тока в цепи при этом растет, а напряжение на батарее уменьшается. | |
Расчетные задачи
1.В безветренную погоду самолет затрачивает на перелет между городами 6 часов. Если во время полета дует боковой ветер перпендикулярно линии полета, то самолет затрачивает на перелет на 9 минут больше. Найдите скорость ветра, если скорость самолета относительно воздуха постоянна и равна 328 км/ч.
Ответ:
| Образец возможного решения (рисунок не обязателен) | |
Уравнение движения для перелета в первом случае: 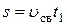 ,
где ,
где 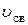 – скорость самолета относительно воздуха.
Закон сложения скоростей в векторном виде для перелета во время ветра: – скорость самолета относительно воздуха.
Закон сложения скоростей в векторном виде для перелета во время ветра: 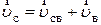 ,
где ,
где 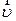 с – скорость самолета относительно Земли, с – скорость самолета относительно Земли, 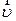 в – скорость ветра. в – скорость ветра.
| 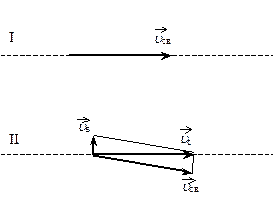
|
| Выражение для скорости самолета относительно Земли во втором случае имеет вид: Тогда уравнение движения для перелета во втором случае:
Следовательно, Ответ: | |
2.Грузы массами M = 1 кг и m связаны лёгкой нерастяжимой нитью, переброшенной через блок, по которому  нить может скользить без трения (см. рисунок). Груз массой M находится на шероховатой наклонной плоскости (угол наклона плоскости к горизонту a = 30°, коэффициент трения m = 0,3). Чему равно максимальное значение массы m, при котором система грузов ещё не выходит из первоначального состояния покоя?
нить может скользить без трения (см. рисунок). Груз массой M находится на шероховатой наклонной плоскости (угол наклона плоскости к горизонту a = 30°, коэффициент трения m = 0,3). Чему равно максимальное значение массы m, при котором система грузов ещё не выходит из первоначального состояния покоя?
| Образец возможного решения |
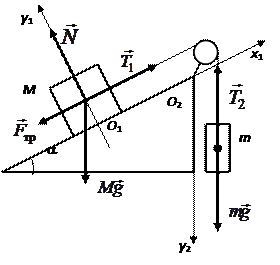 1. Если масса m достаточно велика, но грузы ещё покоятся, то сила трения покоя, действующая на груз массой M, направлена вниз вдоль наклонной плоскости (см. рисунок).
2. Будем считать систему отсчета, связанную с наклонной плоскостью, инерциальной. Запишем второй закон Ньютона для каждого из покоящихся тел в проекциях на оси введенной системы координат: 1. Если масса m достаточно велика, но грузы ещё покоятся, то сила трения покоя, действующая на груз массой M, направлена вниз вдоль наклонной плоскости (см. рисунок).
2. Будем считать систему отсчета, связанную с наклонной плоскостью, инерциальной. Запишем второй закон Ньютона для каждого из покоящихся тел в проекциях на оси введенной системы координат:
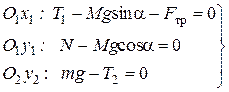 Учтем, что
Учтем, что
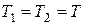 (нить легкая, между блоком и нитью трения нет), (нить легкая, между блоком и нитью трения нет),
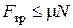 (сила трения покоя).
Тогда (сила трения покоя).
Тогда
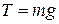 , ,
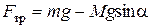 , ,
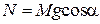 ,
и мы приходим к неравенству ,
и мы приходим к неравенству
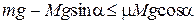 с решением
с решением
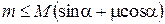 .
Таким образом, .
Таким образом,
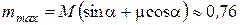 кг. кг.
|
3.Шайба массой m начинает движение по желобу AB из точки А из состояния покоя. Точка А расположена выше точки В на высоте H = 6 м. В процессе движения по желобу механическая энергия шайбы из-за трения уменьшается на ΔE = 2 Дж. В точке В шайба вылетает из желоба под углом a = 15° к горизонту и падает на землю в точке D, находящейся на одной горизонтали с точкой В (см. рисунок). BD = 4 м. Найдите массу шайбы m. Сопротивлением воздуха пренебречь.

Ответ:
| Образец возможного решения |
1) Скорость шайбы в точке В определяется из баланса ее энергии в точках А и В с учетом потерь на трение: 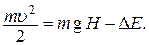 Отсюда
Отсюда 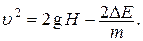 2) Время полета шайбы из точки В в точку D:
2) Время полета шайбы из точки В в точку D:
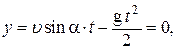 где y – вертикальная координата шайбы в системе отсчета с началом координат в точке В. Отсюда где y – вертикальная координата шайбы в системе отсчета с началом координат в точке В. Отсюда 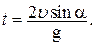 3) Дальность полета BD определяется из выражения для горизонтальной координаты шайбы в той же системе отсчета:
3) Дальность полета BD определяется из выражения для горизонтальной координаты шайбы в той же системе отсчета: 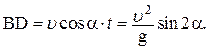 4) Подставляя в выражение для BD значение
4) Подставляя в выражение для BD значение 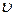 2, получаем 2, получаем 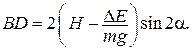 5) Отсюда масса шайбы:
5) Отсюда масса шайбы: 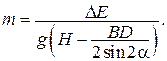 Ответ: m = 0,1 кг.
Ответ: m = 0,1 кг.
|
4.  Небольшая шайба после толчка приобретает скорость
Небольшая шайба после толчка приобретает скорость 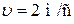 и скользит по внутренней поверхности гладкого закреплённого кольца радиусом
и скользит по внутренней поверхности гладкого закреплённого кольца радиусом 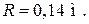 На какой высоте h шайба отрывается от кольца и начинает свободно падать?
На какой высоте h шайба отрывается от кольца и начинает свободно падать?
| Образец возможного решения |
В момент отрыва от кольца на высоте h шайба имела скорость u, определяемую из закона сохранения энергии:
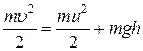 . .
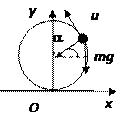 При этой скорости ее центростремительное ускорение При этой скорости ее центростремительное ускорение 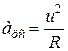 в инерциальной системе отсчета Оху, связанной с Землёй, в соответствии со вторым законом Ньютона обеспечивалось составляющей силы тяжести, действующей на шайбу и направленной к центру кольца: в инерциальной системе отсчета Оху, связанной с Землёй, в соответствии со вторым законом Ньютона обеспечивалось составляющей силы тяжести, действующей на шайбу и направленной к центру кольца:
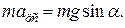 Учитывая, что
Учитывая, что 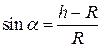 , исключим из системы уравнений ацс и u: , исключим из системы уравнений ацс и u:
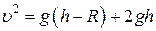 .
Отсюда .
Отсюда 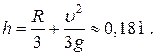 Ответ:
Ответ: 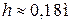 . .
|

|
5. Два параллельных друг другу рельса, лежащих в горизонтальной плоскости, находятся в однородном магнитном поле, индукция 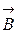 которого направлена вертикально вниз (см. рисунок). Левый проводник движется вправо со скоростью
которого направлена вертикально вниз (см. рисунок). Левый проводник движется вправо со скоростью 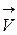 ,а правый – покоится.С какой скоростью
,а правый – покоится.С какой скоростью 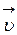 надо перемещать правый проводник (такой же), чтобы в три раза уменьшить силу Ампера, действующую на левый проводник? (Сопротивлением рельсов пренебречь.)
надо перемещать правый проводник (такой же), чтобы в три раза уменьшить силу Ампера, действующую на левый проводник? (Сопротивлением рельсов пренебречь.)
| Образец возможного решения |
Когда правый проводник покоится, на левый действует сила Ампера F = IBl, где 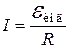 – индукционный ток, R –сопротивление цепи, l – расстояние между рельсами. Поскольку силу Ампера надо уменьшить втрое, ЭДС индукции – индукционный ток, R –сопротивление цепи, l – расстояние между рельсами. Поскольку силу Ампера надо уменьшить втрое, ЭДС индукции 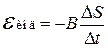 в контуре надо в три раза уменьшить. Значит, скорость изменения площади, ограниченной контуром, также должна быть меньше в три раза. Отсюда следует, что правый проводник должен, как и левый, двигаться вправо, причем его скорость должна быть равна в контуре надо в три раза уменьшить. Значит, скорость изменения площади, ограниченной контуром, также должна быть меньше в три раза. Отсюда следует, что правый проводник должен, как и левый, двигаться вправо, причем его скорость должна быть равна 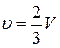 . .
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
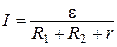 .
.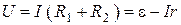 .
.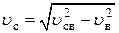 .
.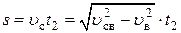 .
.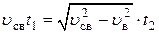 , Отсюда:
, Отсюда: 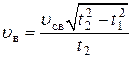 .
.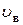
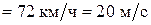 .
.