
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Дополнительные задания. выполняете по желанию на дополнительную оценку). Ниже имеются образцы решений.
Дополнительные задания
(выполняете по желанию на дополнительную оценку). Ниже имеются образцы решений.
1. Напишите уравнение сферы радиуса R с центром А, если:
а) А(3; -2; 1) и R = 7 дм;
б) А(0; 0; 2) и R = 5 м.
2. Найдите координаты центра точки Аи радиус сферы, заданной уравнением:
а) 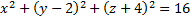
б) 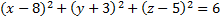
3. Напишите уравнение сферы с центром А, проходящей через точку N, если
А(7; 6; -5) и N(2; -3; 8).
4. Найдите площадь сферы, если радиус сферы равен:
а) 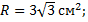
б) 
5. Площадь сферы равна 256π см2. Найдите радиус сферы.
6. Найдите объем шара, если радиус R равен 0,75 см.
7.Найдите радиус шара, если объем шара равен 576π м3
Образец выполнения заданий:
1. Напишите уравнение сферы радиуса R с центром А, если:
а) А(2; -4;7), R = 3;
б) А(0;0;0), R = ;
в) А(2;0;0), R = 4;
| Дано: | Решение: |
а) А(2; -4;7), R = 3;
б) А(0;0;0), R = 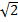 ;
в) А(2;0;0), R = 4. ;
в) А(2;0;0), R = 4.
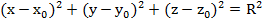
| Уравнение сферы:
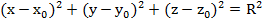 а)
а) 
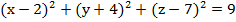 б)
б) 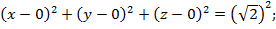
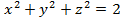 в)
в) 

|
| Ответ: а) б) в) | |
2. Найдите координаты центра и радиус сферы, заданной уравнением:
а) 
б) 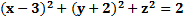
| Дано: | Решение: |
а) 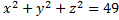 б)
б) 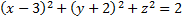
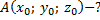 R - ?
R - ?
| Уравнение сферы:
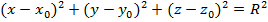 а)
а) 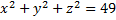 А(0; 0; 0), т.к. координаты
А(0; 0; 0), т.к. координаты 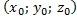 отсутствуют в данном выражении. отсутствуют в данном выражении.

 А(3; -2; 0),
А(3; -2; 0), 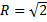
|
Ответ: А(3; -2; 0), 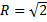
|
3. Напишите уравнение сферы с центром А, проходящей через точку N, если:
а) А(-2; 2; 0), N(0; 0; 0)
б) А(-2; 2; 0), N(5; 0; 1)
| Дано: | Решение: |
а) А(-2; 2; 0), N(0; 0; 0)
б) А(-2; 2; 0), N(5; 0; 1)
в) А(0; 0; 0), N(5; 3; 1)
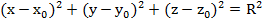 R - ?
R - ?
| Радиус R будет равен расстоянию между двумя точками – А( 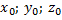 ) и N( ) и N( 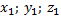 ). ).


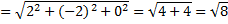 Уравнение сферы:
Уравнение сферы: 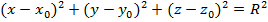 , где , где
 координаты точки центра сферы – координаты точка А( координаты точки центра сферы – координаты точка А( 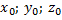 ). ).
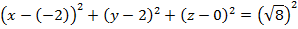
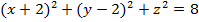
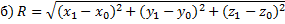
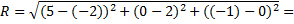
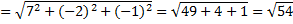 Уравнение сферы:
Уравнение сферы: 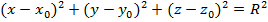 , где , где
 координаты точки центра сферы – координаты точка А( координаты точки центра сферы – координаты точка А( 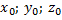 ). ).
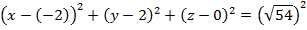
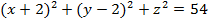
|
| Ответ:
| |
4. Найдите площадь сферы, если радиус равен:
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
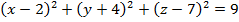
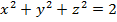
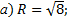
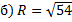 ;
;