
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Прямая на плоскости
Прямая на плоскости
1. Дана прямая 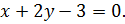 Выяснить какие из точек
Выяснить какие из точек 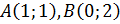 и
и 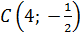 принадлежат данной прямой.
принадлежат данной прямой.
Решение.
Для того, чтобы определить, принадлежит ли точка данной прямой необходимо подставить координаты точки в уравнение прямой.
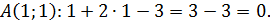
Получили верное равенство, значит, точка 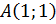 принадлежит прямой
принадлежит прямой 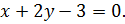
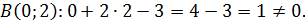
Получили неверное равенство, значит, точка  не принадлежит прямой
не принадлежит прямой 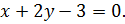
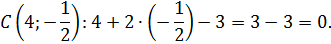
Получили верное равенство, значит, точка 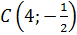 принадлежит прямой
принадлежит прямой 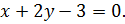
2. Написать уравнение прямой 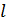 , проходящей через точки
, проходящей через точки 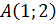 и
и 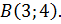
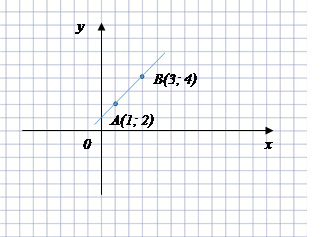 Решение.
Решение.
Для начала необходимо найти направляющий вектор 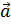 . В качестве начальной точки можно выбрать любую из двух данных, например,
. В качестве начальной точки можно выбрать любую из двух данных, например, 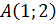 . В качестве направляющего вектора, мы будем использовать вектор, имеющий начало в точке
. В качестве направляющего вектора, мы будем использовать вектор, имеющий начало в точке 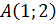 и конец в точке
и конец в точке 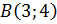 . Координаты направляющего вектора определяются следующим образом:
. Координаты направляющего вектора определяются следующим образом:
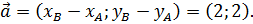
Мы рассмотрим разные виды уравнений, задающих прямую линию на плоскости.
1) Каноническое уравнение прямой.
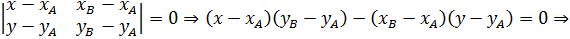
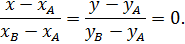
Подставляя координаты данных точек, получаем каноническое уравнение прямой 
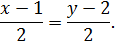
2) Уравнение прямой с угловым коэффициентом.
Уравнение прямой с угловым коэффициентом имеет вид:
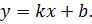
Из канонического уравнения прямой имеем:
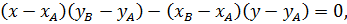
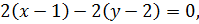
откуда, выражая 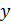 , получаем уравнение прямой
, получаем уравнение прямой 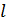 с угловым коэффициентом:
с угловым коэффициентом:
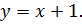
3) Параметрическое уравнение прямой.
Параметрическое уравнение прямой имеет вид:
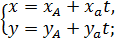
где 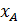 ,
, 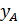 – координаты точки, принадлежащей прямой,
– координаты точки, принадлежащей прямой,  – координаты направляющего вектора
– координаты направляющего вектора 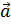 .
.
Параметрическое уравнение прямой 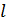 будет иметь вид:
будет иметь вид:
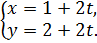
4) Общее уравнение прямой.
Из канонического уравнения прямой
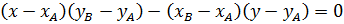
можно получить общее уравнение прямой
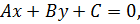
где 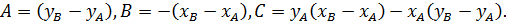
Общее уравнение прямой 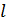 будет иметь вид:
будет иметь вид:
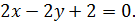
3. Вершины треугольника находятся в точках 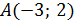 ,
, 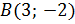 и
и 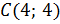 . Написать уравнения сторон треугольника, уравнение средней линии
. Написать уравнения сторон треугольника, уравнение средней линии 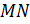 и уравнение высоты
и уравнение высоты 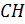 и уравнение прямой, проходящей через точку
и уравнение прямой, проходящей через точку 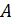 , параллельно стороне
, параллельно стороне 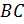 .
.
Решение.
Для того, чтобы найти стороны треугольника, используем формулу уравнения прямой, заданной двумя точками:
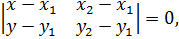
где 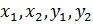 – соответствующие координаты заданных точек.
– соответствующие координаты заданных точек.
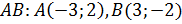 ,
,
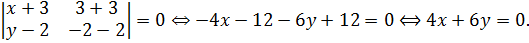
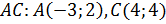 ,
,
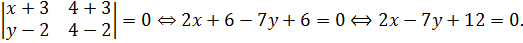
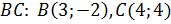 ,
,
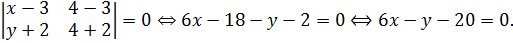
Пусть 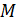 – середина стороны
– середина стороны 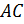 ,
,  – середина стороны
– середина стороны  , найдем координаты точек
, найдем координаты точек 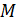 и
и 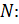
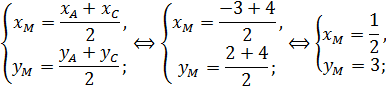
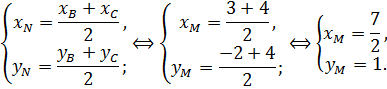
Теперь найдем уравнение прямой 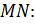
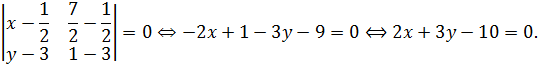
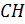 – высота, проведенная к стороне
– высота, проведенная к стороне 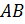 , значит, для того, чтобы найти уравнение
, значит, для того, чтобы найти уравнение 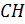 , нам понадобится вектор нормали (перпендикулярный вектор)
, нам понадобится вектор нормали (перпендикулярный вектор) 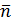 к прямой
к прямой 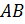 .
.
Пусть прямая 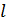 задана общим уравнением
задана общим уравнением  , тогда вектор нормали прямой
, тогда вектор нормали прямой 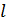 задается координатами
задается координатами 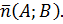
В нашем случае, вектором нормали 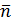 к прямой
к прямой 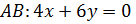 будет вектор с координатами
будет вектор с координатами  Так как высота
Так как высота 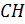 – это перпендикуляр, опущенный из вершины
– это перпендикуляр, опущенный из вершины 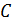 на прямую
на прямую 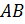 , то вектор
, то вектор 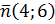 будет направляющим для
будет направляющим для 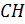 . Составим уравнение прямой, заданной точкой и направляющим вектором:
. Составим уравнение прямой, заданной точкой и направляющим вектором:
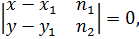
где 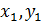 – координаты данной точки,
– координаты данной точки,  – координаты направляющего вектора.
– координаты направляющего вектора.
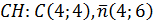 ,
,
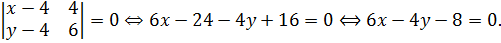
Теперь проведем прямую 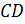 , параллельную стороне
, параллельную стороне 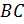 . В общем виде уравнение будет иметь вид:
. В общем виде уравнение будет иметь вид:  , где
, где 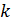 – любое число. При этом должно выполнятся, что точка
– любое число. При этом должно выполнятся, что точка 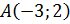 принадлежит прямой
принадлежит прямой 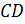 . Подставим координаты точки
. Подставим координаты точки 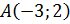 в уравнение прямой
в уравнение прямой 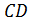 :
:
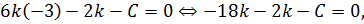
откуда получаем зависимость  . Возьмем
. Возьмем 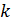 =1, тогда
=1, тогда  , уравнение прямой
, уравнение прямой 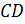 имеет вид:
имеет вид:
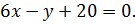
4. Установить, при каком значении 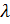 прямые
прямые 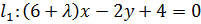 и
и 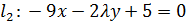 параллельны?
параллельны?
Решение.
Две прямые  и
и 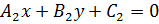 параллельны, если существует такое число k, при котором соответствующие коэффициенты при
параллельны, если существует такое число k, при котором соответствующие коэффициенты при 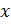 и
и 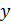 пропорциональны:
пропорциональны: 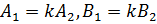 , а свободный коэффициент – нет:
, а свободный коэффициент – нет: 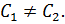
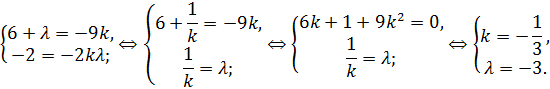
Таким образом, при 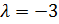 данные прямые будут параллельны, а их уравнения будут иметь вид:
данные прямые будут параллельны, а их уравнения будут иметь вид: 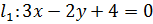 и
и 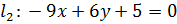 .
.
5. Исследовать взаимное расположение прямых 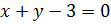 и
и 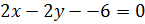 .
.
Решение.
Предположим, что прямые параллельны или совпадают, тогда существует такое число k, при котором соответствующие коэффициенты при 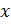 и
и 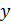 пропорциональны:
пропорциональны: 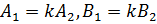 :
:
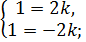
Очевидно, что полученная система не совместна, а значит, прямые пересекаются. Тогда должно выполняться, что
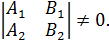
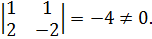
Получили, что прямые пересекаются. Найдем точку их пересечения:
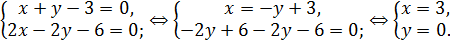
Получаем точку пересечения данных прямых (3; 0).
6. Найти на оси Ox точку M удаленную от прямой 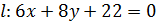 на расстояние равное 4.
на расстояние равное 4.
Решение.
Так как точка M принадлежит оси Ox, то ее координаты будут иметь вид 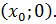 Воспользуемся формулой для вычисления расстояния от точки до прямой:
Воспользуемся формулой для вычисления расстояния от точки до прямой:

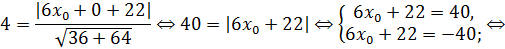
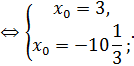
Получаем две точки 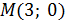 и
и 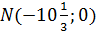 , удаленных от прямой
, удаленных от прямой 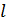 на расстояние равное 4.
на расстояние равное 4.
7. Найти расстояние между прямыми 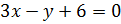 и
и 
Решение.
Найдем точку, принадлежащую прямой 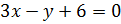 – это точка A(1; -3). Найдем расстояние от точки A до прямой
– это точка A(1; -3). Найдем расстояние от точки A до прямой 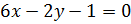 :
:

8. Найти угол, образованный прямыми  и
и 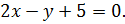
Решение.
Предположим, что прямые пересекаются или совпадают, тогда существует такое число k, при котором соответствующие коэффициенты при 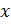 и
и 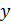 пропорциональны:
пропорциональны: 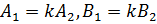 :
:

Очевидно, что это не так, значит, прямые пересекаются.
Воспользуемся формулой:
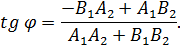
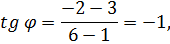
получаем, что угол между данными прямыми 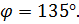
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|